Medical image encryption using chaotic map improved advanced encryption standard

With the progression in network communication, sensitive data is being stored, transmitted and maintained electronically. This is becoming a growing concern for medical organisations which must adhere to the Health Insurance Portability and Accountability Act (HIPAA). This means organisations must ensure: medical images confidentiality (i.e. that the image cannot be accessed by unauthorised parties); integrity (i.e. that images cannot be modified); and authentication (i.e. that the image has been sent to and from the correct sources) [1]. It is these security vulnerabilities that have limited the development of electronic and mobile health applications, which intend to improve the efficiency of medical image communication [2]. Therefore, an improved encryption algorithm is needed which will enable these applications to progress further. Other areas of importance include digital watermarking where the owner’s information is embedded in the image. It’s important that the quality of the image is not degraded in this process [3]. The confidential information stored in the image reinforces the reason as to why it is so important that images are encrypted securely and can be retrieved perfectly after decryption. This paper focuses on the confidentiality of an encrypted image and how an existing medical image encryption algorithm could be improved with a chaotic map.

The Digital Imaging and Communications in Medicine (DICOM) is the current international standard developed by the American College of Radiology (ACR) and National Electrical Manufacturers Association (NEMA) for medical image processing and communication. The Advanced Encryption Standard (AES) and Triple Data Encryption Standard (3DES) can be used for the encryption of medical image data under this standard [4]. AES however, outperforms 3DES and this is due to 3DES having weaker encryption keys and being impracticable with large messages [5].

The procedure used in encryption can be broken down into two stages: the transmission across a network and algorithm used for the encryption of the image [6]. Firstly, it should be noted that in cryptography, data in its original form is referred to as plaintext and encrypted data as ciphertext. There are two types of cryptography: public key (asymmetric) cryptography and secret (symmetric) key cryptography. Public-key cryptography requires the sender and receiver to have two keys; a public key for encryption of the message to the receiver and a private key for the decryption of the message sent. Anyone with access to sender’s public key can encrypt a message to them, but is only able to decrypt the message if they have access to their corresponding private key, see Fig. 1. [6]

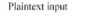
Encryption alvDrillini

Decryption algorithm

Plaintext output

Fig.1. Public key encryption

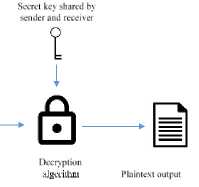
Unlike public-key cryptography, secret-key cryptography requires one key for encryption and decryption. These are often agreed prior to the sending of the message between the sender and receiver, see Fig. 2. [6]

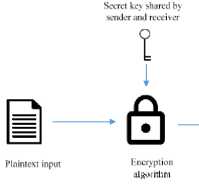
Fig.2. Secret key encryption

In the image encryption process, an algorithm is used with a given key, a secret key for example, which is applied to one-dimensional plaintext to generate the ciphertext. Once this data has been transmitted to the receiver, they will decrypt the ciphertext to retrieve the original plaintext. Traditionally, data is encrypted by block or stream. A block cipher is a method of encryption which divides the plaintext into blocks and encrypts each block one by one. A stream cipher, however typically encrypts one byte at a time. [6]

Images are made up of two-dimensional arrays of data, they must first be treated as a set of one-dimensional arrays, before encryption [7]. As images require significantly more space than one-dimensional text data, they are sometimes compressed to reduce storage space and transmission time. Although this lossy encryption is acceptable for the encryption of general images, medical images are required to be lossless after encryption. A reason for this it that the inability to reconstruct an image exactly as it was before encryption, could result in a potential misdiagnosis [8].

Chaotic algorithms present a possible improvement to the encryption quality. These algorithms have been developed from chaos theory, the theory that a change in an initial condition can impact results drastically [9]. This paper analyses the effect that Arnold’s chaotic cat map has on the encryption quality of images, when it is applied to AES before encryption.

The rest of this paper is structured as follows: related works in Section II, the process of Arnold’s cat map and AES explained in Sections III and IV; our proposed algorithm explained in Section V; discussion of the experimental analysis in Section VI; and the conclusion and future scope in Section VII.

• II.    Related Works

In many research papers, chaotic-based algorithms are now being developed [9-12]. What makes these algorithms different from traditional encryption algorithms is their ergodicity and extreme sensitivity to initial conditions. And it is these properties that are showing improvements in confusion and diffusion, which are essential to the development of a secure encryption algorithm [9].

2D chaotic maps are becoming a common preencryption step to achieve confusion. Meghdad Ashtiyani et al. [11] proposed an algorithm in their paper ’ChaosBased Medical Image Encryption Using Symmetric Cryptography’ which combines Arnold’s cat map with Simplified Advanced Encryption Standard (S-AES). The proposed algorithm makes use of chaos in both the map and the encryption. First, an image is iterated 30 times with Arnold’s cat map followed by encryption with SAES. In S-AES, the generation of the substitution box uses Lorenz chaotic mapping in the encryption. The algorithm of Meghdad Ashtiyani et al. was tested on 256*256 mammography image with 8-bit intensity and the results showed an “adequate level of security” where the encrypted image had a uniform histogram. The main disadvantage of iterating through Arnold’s cat map as a pre-encryption step is that it increases the overall encryption time, and this may be unsuitable for the required transmission time over public networks. Encryption time should be short relative to transmission time [12].

This paper looks more specifically into how the cat map affects the encryption quality; it examines 16-bit DICOM images instead of the 8-bit images tested on in Meghdad Ashtiyani et al. paper [11]. Our proposed algorithm, similar to Meghdad Ashtiyani et al. algorithm, also uses Arnold’s cat map as a pre-encryption step. However, we only make use of chaos in this step. Instead of S-AES, we have used AES as our encryption algorithm to be compliant with the DICOM standard. Our developed algorithm CAT-AES iterates the image through Arnold’s cat map a calculated number of times, followed by a horizontal stretch and encryption in AES before un-stretching the image back to its original size. Our implementation of the standard AES algorithm has the exact same structure as CAT-AES without the preencryption cat map step.

• III.    Arnold’S Cat Map

Arnold’s cat map is a 2D chaotic map which, when applied to an image, scrambles the pixels. Interestingly, the original image reappears when the map is iterated at a certain number of times [13].

The map is composed of three steps: a shear of a factor of 1 in the x-direction, a shear of a factor of 1 in the y-direction and the evaluation of the modulo n [11], [13]. This is defined as follows:

р(х,у) = [1 1] [y]mоd(n) (1)

where P(x, y) is the transformed gray-scale pixel value at index (x,y) in the n*n image. The mod operator stands for modular, taking the remainder when we divide the resulting matrix value by the image dimension n.

In Fig. 3. the cat map has been applied to a 256*256 brain MRI. Fig. 3(a) shows the original image. Fig. 3(b)

shows the first iteration of the cat map, the brain is sheared, and its modulus is evaluated, but its overall pattern is still quite evident. In Fig. 3(c) at 31 iterations it begins to get hard to make out the brain, but at Fig. 3(d) at 48 iterations visible patterns of the brain start to reappear. In Fig. 3(e), we see the effect of chaos that the cat map has had on the image, where there are no visible patterns that can be seen with the naked eye. In Fig. 3(f) and Fig. 3(g) both images share stronger visible patterns with the original image. The shearing of the image can clearly be seen. In Fig. 3(h) at the 96th iteration, there is a clear similarity in the correlation with the original image. Using the 96th iteration as a midpoint, the previous and remaining iterations are symmetrical. Fig. 3(g). and Fig. 3(i), Fig. 3(f) and Fig. 3(j), Fig. 3(e) and Fig. 3(k), Fig. 3(d) and Fig. 3(l), Fig. 3(c) and Fig. 3(m), Fig. 3(b) and Fig. 3(n). Finally, the original image appears unchanged in Fig. 3(o) at 192 iterations.

Р (1,2) = [1  Ж]то d(256) = [^]

Р (1,3) = [1  1Ш]то ^(256) = [4]

^{Р (1,4)} = ^[ 1 2 ^]Й^{то d(256}H 9 ^]

р(1,256)=[1  2] [256]^(256)=[1]  (2)

The cat map only shuffles the pixels in the image; it is not secure enough for it to be used as the encryption itself. The original image could easily be retrieved by applying the remaining cat map iterations to the image. Therefore, an encryption algorithm must be used to change the pixel data [11].

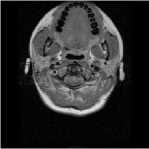
(a) Iteration 0

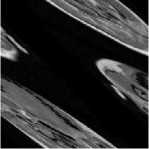
(b) Iteration 1

(c) Iteration 31

(d) Iteration 48

(e) Iteration 90

(f) Iteration 94

(g) Iteration 9 5

(h) Iteration 96

(i) Iteration 97

IV. Advanced Encryption Standard (Aes)

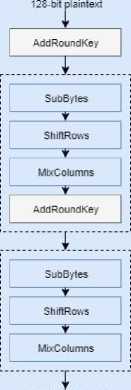
AES is a block cipher that encrypts a 128-bit block at a time. It is composed of four steps: SubBytes, ShiftRows, MixColumns, and AddRoundKey, which are repeated in rounds. The number of rounds is determined by the key size which can be 128 bits, 192 bits or 256 bits and results in 10, 12 or 14 rounds respectively. The rounds follow the order in all rounds except the first and last. The first round begins with an additional AddRoundKey step and the last round has no MixColumn step. [7]

AES is also configured using a mode that changes the way in which the blocks of data are encrypted. Cipherblock chaining (CBC) mode is one of the configurations that can be used. It first applies the initialization vector only to the first block of plaintext and then applies the bitwise XOR operation to the ciphertext of the first block and input of the next block. The bitwise XOR operation is repeated until the last block of plaintext, see Fig. 4 [7]. This mode provides better security when similar patterns are shared in the blocks of plaintext.

(j) Iteration 98

(k) Iteration 102

(l) Iteration 144

(m) Iteration 161

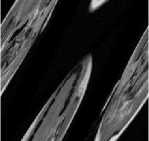
(n) Iteration 191

Fig.3. Arnold’s cat map applied to a brain MRI at certain iterations

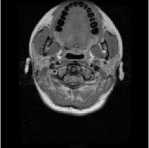
(o) Iteration 192

The cat map would be computed as follows for the first row of a 256*256 image:

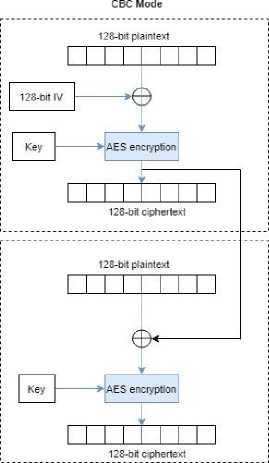
Fig.4. AES encryption process in CBC mode

AES encryption

е

128-bit ciphertext

р (1,1) = [1 1][1]mo d(256) = [2]

V. Proposed Algorithm

Two algorithms have been used in this paper AES and our developed algorithm, CAT-AES, which is based on the algorithm proposed by Meghdad Ashtiyani et al. [11]. We have implemented AES to take a 16-bit DICOM image as input and then expand it horizontally. This is done by dividing each 16-bit pixel into two 8-bit pixels. AES encryption is then applied, followed by the concatenation of adjacent pixels, back into single 16-bit pixels to form the encrypted image. CAT-AES has the same structure, with an additional step, which applies the cat map iteratively ^catMap times before the encryption, see Fig. 5. Both algorithms use the same key and initialization vector (IV) and were tested on two set of images, to see how the cat map step affects the encryption quality. AES encryption only makes use of the initialization vector of CBC mode, due to the method of encryption there is no bitwise XOR between the corresponding blocks of input.

In this section, an explanation is provided for the number of times the cat map should be iterated, followed by how the algorithms were computed.

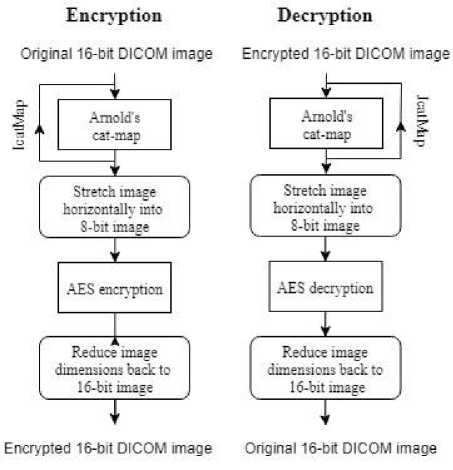
Fig.5. CAT-AES encryption process. The process for AES has the same structure, without the cat map step.

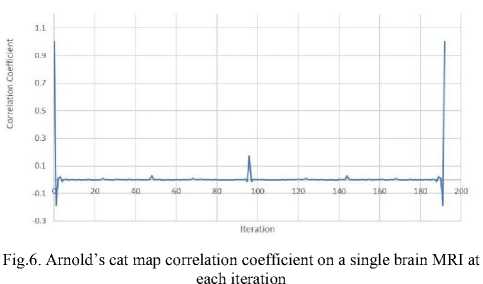
To find an iteration for the cat map to use for the proposed algorithm, two tests were carried out on 16-bit 256*256 brain MRI images. The first test involved calculating the correlation coefficient at every iteration of the cat map until the original image reappeared, see Fig. 6. It was found that the correlation coefficient peaked at 96th iteration, with the highest correlation coefficient and resembling the original image the most. This was also the half-way point until the original image reappeared at 192 iterations, refer to Fig. 3.

The second test consisted of calculating the absolute average correlation coefficient on 20 16-bit 256*256 brain MRI between the range of 86-106 iterations, see Fig. 7. This range was decided based on the outcome of the first test which showed smaller correlation coefficients around the halfway point before the image reappears. It was found that in this range, iterations 90 and 102, both symmetrical, had the smallest correlation coefficient of 0.01736266 and therefore resembled the image the least.

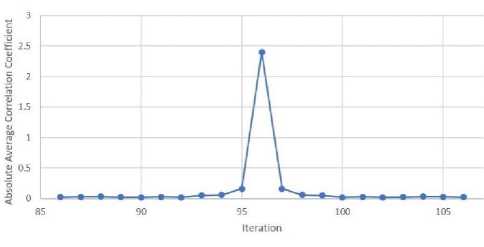
Fig.7. Arnold’s cat map absolute average correlation coefficient on 20 brain MRI images at each iteration

As a result of these tests, Eq. 3a and Eq. 3b were formed to determine the number of times that the cat map should be applied to achieve a reasonably scrambled state.

^catMap = 0.46875∗Ӏ           (3a)

^catMap = 0.53125∗Ӏ           (3b)

Where IcatMap is the number of iterations required to reach a reasonably scrambled state and I is the number of iterations required to retrieve the original image after applying the cat map. We can use either Eq. (3a) or Eq. (3b) as the iteration for the cat map because of the symmetry observed in Fig. 7.

On decryption, the rest of the cat map was iterated through: for 90 out of 192 iterations of the cat map, the remaining 102 iterations are iterated during decryption to retrieve the original image.

JcatMap =   ^- I cat Map

When dealing with different image sizes, I in Eq. 3(a), Eq. 3(b) and Eq. 4 will change based on the image dimensions.

• A.    Arnold’s Cat Map

Procedure 1 shows how the cat map was computed. While iteration i (Eq. 3a) has not been reached, the cat map transformation is calculated for each pixel and stored in NewX and NewY. This is then assigned to CatMapImg in the new position and is repeated until the i=Counter. Once completed, the image pixels are scrambled.

• B.    Image Expansion

Image expansion is needed to encrypt the 16-bit image as 16 8-bit blocks for AES encryption. The 16-bit image is expanded which involves splitting each 16-bit pixel into two sets of 8-bit pixels. This results in a horizontal image stretch. Fig. 8. shows how this works. Take a sample of 4 pixels: A, B, C and D which are 16 bits, they are each split into two 8-bit pixels, A1 and A2, B1 and B2, C1 and C2, and so on. This process is applied to every pixel in the image. Refer to Procedure 2 to see how this was computed.

• C.    AES Encryption

AES is used with a 128-bit key in CBC mode. First, the key, s-box and initialization vector (IV) are generated. This is followed by the division of each row of the expanded 8-bit image into 128-bit blocks. Each block is then encrypted, and all adjacent pixels are concatenated back into single 16-bit pixels. This process is repeated row by row to form the encrypted image; which has the same dimensions of the original image. Refer to procedure 3.

Procedure 2: Image Expansion

6 7

V

HI 11

Input : lmg,CarMaplmg

Explmg 4— KBit/mage^lmgHeight, ImgWidth * 2) for i=l to ImgHeight do for j=l to ImgWidth do

CurrentPixel = CatMapImg(ij)

Explmg. AppendPixel(Pixel 1)

Explmg. AppenxPixel(Pixe 12) end end в Output: Explmg

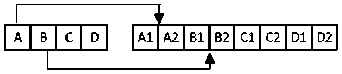
Fig.8. Expansion process

Procedure 3: AES Encryption

i

S

1(1 JI 12 13

Input : Explmg Eitcryptedlmg 4— EmptyMat rixlJmgW idth, ImgHeight) key 4— generateKeyO sBox 4— generareShox(key)

• IV 4— gene rate IV ()

foreach rowinExpImg do

DivideRowlnto 128bitBlocks(ExpImg) foreach \2Kbitblock do

VI. Experimental Analysis

The experiment was tested using MATLAB on a Windows 7 machine (Intel i5-4570 at 3.20 GHz). The two algorithms AES and CAT-AES were evaluated on two 16-bit sets of DICOM images: one set of 20 brain MRI images with dimensions of 256*256 and one set of 26 breast cancer MRI images with 320*320-pixel dimension. Encryption with CAT-AES iterated the cat map 90 times (Eq. 3a) for the first set of images and 127 times (Eq. 3b) for the second set. Both algorithms were also evaluated on a third set of 12-bit intensity images: 26 thigh MRI images with dimensions of 256*256. For this set of images, the CAT-AES algorithm iterates the cat map 102 times (Eq. 3b) before encryption with AES.

The statistical analysis metrics used to assess the encryption quality were correlation coefficient and the histogram uniformity. These were calculated using the MATLAB functions corr2() and histogram() for the original images and corr2() and imhist() for the encrypted image. We have also calculated the mean, standard deviation and average encryption time across the first two sets of images.

Correlation Coefficient measures the quality of encryption on an image; a comparison between pixels at the same position in the original and encrypted image. The correlation coefficient ranges between -1 and +1, the aim is to get a value closest to zero as it shows less similarities to the original image. In this analysis, the absolute correlation coefficient has been used to analyse how well the encryption algorithms perform. [7]

The absolute correlation coefficient was calculated as follows:

|

^∑ т ^∑n ( ^тп

^- А )( ^тп ^- В )

√(∑ т ^∑ п ( А

тп

^- А ) )(∑ т ^∑ п ( ^тп ^- В ))

|

(5a)

^^^^

А =      ( )               (5b)

^^^^^

в =       ( )                (5c)

The Histogram Uniformity is a bar graph which shows how often each intensity occurs in the image. It is calculated by dividing the intensity range into a number of bins. These bins are incremented for every pixel occurrence in that range. The horizontal axis represents the intensity levels and the vertical axis represents the number of occurrences of that intensity. The aim of Histogram Uniformity is to get the intensities as uniform as possible so that it is hard to detect any trends in the data. As 16-bit images have been used for testing, the intensity range is from 0-65535. [7]

• A.    Correlation Coefficient Analysis

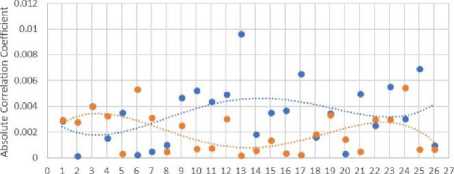
In both Fig. 9 and Fig. 10 the absolute correlation coefficient is calculated against the original and encrypted images using in both polynomials (calculated to the order of 4) which is always close to zero in Fig. 9 and mostly closer to zero for the CAT-AES encryption in Fig. 10. Overall the absolute correlation coefficient was closer to zero in 17 out of out of 20 of the brain MRI images and 17 out of 26 of the breast-cancer MRI images.

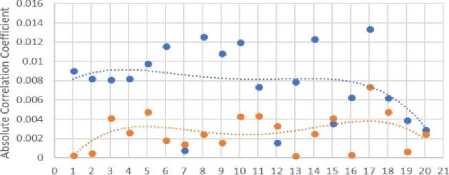
Fig.9. Absolute correlation coefficient on 20 256*256 brain MRI

Image

Fig.10. Absolute correlation coefficient on 26 320*320 breast cancer MRI

The mean and standard deviation was also calculated on the absolute correlation coefficient values, seen in Fig. 11. It can also be seen here that encryption with CAT-AES is closer to zero. Therefore, the images encrypted with CAT-AES share fewer trends in the intensity compared to the images encrypted with AES.

• B.    Histogram Uniformity

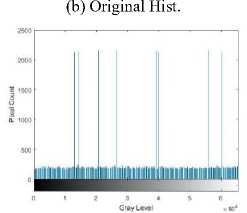
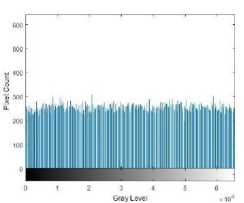
In Fig. 12(a) and 12(b) the original brain image has a large amount of around 30,000 black pixels with intensity 0, most of which surrounds the brain to the left and right of the image. This has had an impact on AES encryption, see Fig. 12(c), which shows clear trends to the left and right of the image. This is evident in the histogram Fig. 12(d) which shows a number of high-intensity occurrences. Encryption with CAT-AES in Fig. 12(e) however, appears a lot more uniform, this is seen in the histogram in Fig. 12(f). What is interesting is that the only difference between these two algorithms is the cat map, perhaps the combination of the cat map and pixel expansion before encryption is what has a positive impact on the encryption quality.

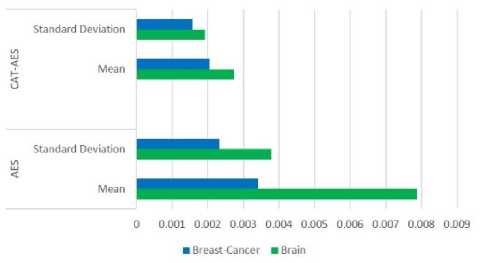
Fig.11. Mean and Standard Deviation on the absolute correlation coefficient of 26 breast cancer MRI and 20 brain MRI

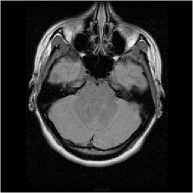
(a) Original

(c) AES

(d) AES Hist.

(e) CAT-AES

(f) CAT-AES Hist.

Fig.12. Brain encryption images and histograms

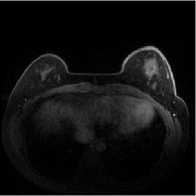
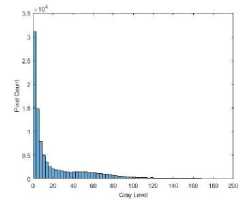
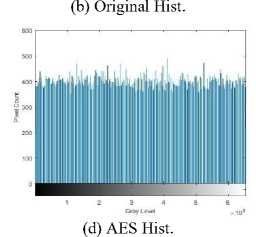
Both encryption algorithms performed better on the breast cancer MRI set which has larger image dimensions of 320*320 and less of an intensity range, see Fig. 13(a) and 13(b). It’s hard to see the difference between the encrypted images, Fig. 13(c) and 13(e), but the respective histograms are both uniform, see Fig. 13(d) and 13(f). Encryption with CAT-AES has fewer intensity peaks in its histogram, the pixel count is more uniform and closer to 400 across the intensity range.

(a) Original

(c) AES

(e) CAT-AES

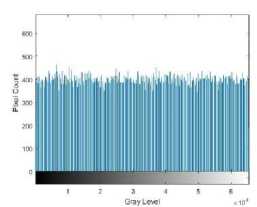
(f) CAT-AES Hist.

Fig.13. Breast cancer encryption images and histograms

• C.    Time Analysis

Table 1 and Table 2 shows the average time taken per slice to encrypt and decrypt the images. As expected CAT-AES encryption took longer because of the additional cat map step. The cat map took 25.1% of the encryption time and 23.9% of the decryption time for the brain image, 19.9% of the encryption time and 22.8% of the decryption time for the breast cancer image.

• D.    Additional Results

Both algorithms were also tested on one set of 26 12-bit thigh MRI images. These images were padded with zeros to 16-bits before encryption when using the MATLAB dicomread() function.

In Fig. 14 the images encrypted with CAT-AES have a lower absolute correlation coefficient in 16 out of 26 of the thigh MRI images. The majority of images encrypted with AES peak with a higher absolute correlation coefficient at 0.18 in comparison to the images encrypted with CAT-AES. This is evident in the AES polynomial curve which is significantly higher than the CAT-AES polynomial curve.

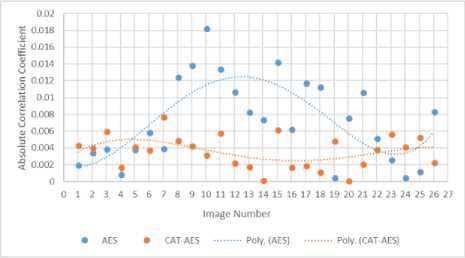
Fig.14. Absolute correlation coefficient on 26 320*320 breast cancer MRI

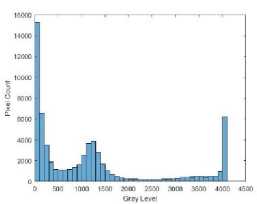
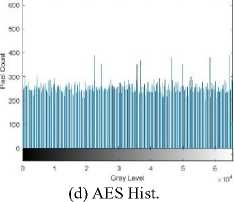
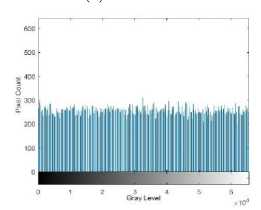
In Fig. 15 the original, AES encrypted, and CAT-AES encrypted thigh image is shown with their respective histograms. This is the 14 ^th image seen in Fig. 14. In Fig. 15(a) the thigh image has more lighter pixels compared to the brain and breast cancer images. This can be seen in Fig. 15(b) compared to Fig. 12(b) and Fig. 13(b). The AES encrypted image has a high intensity pixel count to the left and right of the image in Fig. 15(c). Evident in the histogram 15(d). Although this is not as apparent in comparison to the brain image encrypted with AES in Fig. 12(c), it still affects the encryption quality. In Fig. 15(e)

the image is not blurred and shows no clear intensity trends. This is validated by the histogram which is more uniform in Fig. 15(f).

• E.    Discussion

CAT-AES generally performed well on the sets of medical images that we have tested on. In comparison to Meghdad Ashtiyani et al. results [11] we have processed higher intensity 16-bit images and we also see a uniform histogram across both images. We have also taken the mean and standard deviation on multiple images and CAT-AES shows improvements on both sets. The absolute correlation coefficient appears closer to zero on the majority of images tested on. These results show that there is a sufficient level of security provided by this algorithm. Although the pixel data is never changed until the encryption of the image. It is interesting to see that shuffling the pixels before encryption has had a positive impact on the encryption quality.

Table 1. Average Time (Second) per Slice on Encryption/Decryption of the Brain MRI

AES			CAT-AES
Expansion	Encryption	Total	Cat Map	Expansion	Encryption	Total
6.52	14.61	21.13	13.83	6.43	14.45	34.72
Expansion	Decryption	Total	Expansion	Decryption	Cat Map	Total
6.55	15.27	21.82	6.45	15.16	15.50	37.11

Table 2. Average Time (Second) per Slice on Encryption/Decryption of the Breast-cancer MRI

AES			CAT-AES
Expansion	Encryption	Total	Cat Map	Expansion	Encryption	Total
8.40	18.84	27.24	26.74	7.63	18.81	53.18
Expansion	Decryption	Total	Expansion	Decryption	Cat Map	Total
8.44	19.94	28.38	8.85	21.34	23.59	53.78

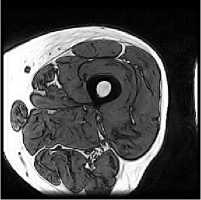
(a) Original

(b) Original Hist.

(c) AES

(e) CAT-AES

(f) CAT-AES Hist.

Fig.15. Thigh encryption images and histograms

VII. Conclusion and Future Scope

Two algorithms were used in this paper AES and CAT-AES. Both algorithms were tested on three sets of DICOM images: 20 brain MRI images, 26 breast-cancer MRI images. The images were evaluated by the absolute correlation coefficient, mean, standard deviation, histogram uniformity and time analysis. The absolute correlation coefficient was closer to zero when encrypting with CAT-AES on 17 out of 20 of the brain MRI and 17 out of 26 of the breast-cancer MRI. The mean and standard deviation were smaller, and the histograms analysed also appeared more uniform when encrypting with CAT-AES. The time taken to encrypt was longer when encrypting with CAT-AES due to the additional cat map step. Our proposed algorithm can process high-intensity 16-bit DICOM images and has shown improvements to the encryption quality.

To understand more about how the cat map affects the encryption quality of medical images, several tests should be completed on images of different dimensions, bitintensity, colour spectrum. The tests in this image were only completed on square images to allow for the use of the cat map; however, it has been proposed in [12] to expand a non-square image to into a square and use a pseudo-random number generator to pad the extra pixels in a 0-255 intensity range. This intensity range could be expanded for DICOM 16-bit images to 0-65535 and therefore allow the cat map to be used on images that are not initially square. A multi-dimensional cat map such as the one used in [14] could also be used for pre-encryption to see how this affects the encryption quality.

Chaotic maps could also be integrated into AES encryption to make use of their chaotic properties. For coloured MRI scan images, [15] extracts the RGB components and reshapes each into one dimensional arrays. Colour extraction could be used as an additional step after the cat map has been applied to an image. The separate arrays could then be encrypted individually before combining them into an encrypted image.

To conclude, chaos theory states that results are sensitive to its initial conditions. This can be interpreted as the state of an image before it is encrypted. It is evident from the results in this paper that applying a chaotic map to modify the initial state of an image before encryption, can improve the encryption quality.