Медленное течение в плоском канале с поперечными ребрами

Задачи о течении жидкости в каналах с пористой или шероховатой стенками встречаются в разнообразных природных процессах и технических приложениях. В частности, оребрение стенок канала является одним из методов управления структурой потока и позволяет в отдельных случаях снижать сопротивление трения при транспортировке жидкости.

В работе [1] рассмотрена задача о сдвиговом течении Куэтта, вызванном движением гладкой плоскости над оребренной границей. В настоящей работе аналогичным способом решается задача о течении жидкости за счет продольного градиента давления в плоском канале с оребренными стенками.

1.    Постановка задачи © Е.В. Мосина, И.В. Чернышев, 2006

Рассматривается течение вязкой несжимаемой жидкости между двумя параллельными стенками, расположенными на расстоянии 2Н друг от друга. Вдоль стенок, поперек потоку, располагаются ребра высотой ЬН (0 <  b < 1) с периодичностью 2аН (рис. 1а). Свяжем с каналом декартову систему координат, направив ось Озе вдоль канала по направлению среднерасходной скорости, ось Оу перпендикулярно стенкам канала, а ось Oz по ширине канала параллельно ребрам. Расход жидкости через канал, приведенный к единице длины в направлении Oz, равен 2Q.

Предполагаем, что число Рейнольдса течения мало (Re = 2Нри^/р < 1) и справедливо приближение Стокса. Принимая за масштаб длины — половину высоты канала Н, скорости — среднерасходную скорость и₀ = Q/H, а давления — Ро = pQ/H², обезразмеренные уравнения Стокса примут вид

Vp = Av, V • v = 0.                         (1)

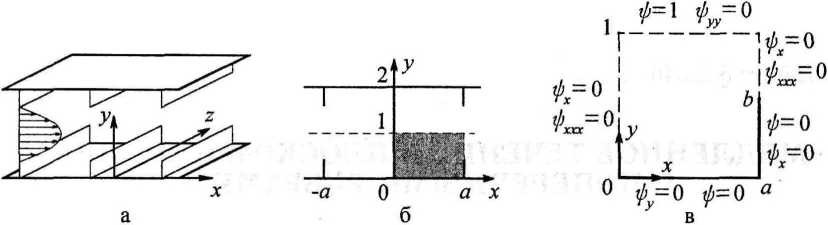
Рис. 1. Оребренный канал:

(а) - геометрия канала; (б) - расчетная область; (в) - граничные условия Исключая из системы (1) давление р и учитывая двумерность постановки, задача сводится к одному бигармоническому уравнению на функцию тока

ДДф = 0.

Учитывая симметричность течения относительно оси канала (у = 1), периодичность по х с периодом 2а, а также симметричность относительно прямых х = 0, х = ±а, рассмотрение краевой задачи можно ограничить прямоугольником (х,у) 6 (0, а) х (0,1) (рис. 16). Граничные условия для функции тока на сторонах этого прямоугольника будут следующими. Условия прилипания на нижней стенке и ребре:

^(гг,О) = О, ^(^.О) = 0,                                 (3)

^(а,у) = 0, ■^_а;(а,у) = 0,      0 <  у < Ь.                  (4)

Периодичность по х и симметрия относительно х = 0 и х = а приводят к условиям:

Ыа,У) = 0, ^(0, у) = 0,

’фххх^) у) — 0, ^жга(О) у) — 0.

ь < у < 1,

Симметрия относительно оси канала и заданный расход жидкости через канал дают

^(ж, !) = °. ФФ^ !) = ^L

Для наглядности условия (3)-(7) вынесены на рис. 1в.

2.    Функция тока

По аналогии с работой [1] решение бигармонического уравнения (2) представим в виде разложения по собственным функциям

ОО                             ОО

<х, у) = Цу) + ^А_п sm(a_ny)Q_n(x) + ^ Ai cos(/3_na;)S_n(y), (8)

П=1                     П=1

где Цу) = А₀уЦ² - Зу + 2) + у,

Q_n(x) - (l-e_n + ac^(l + ej)^

- ^(l-enXe^^-e'0"^),

8Цу) = -2d^e0Ay-^ - е~0А^ + (д _ d^d^

е_п = е~^2аап, d_n = e~²⁰ⁿ, а_п = тт, /З_п = тт/а.

Выражение (8) удовлетворяет только части граничных условий прилипания и симметрии: первым в (3) и (5), второму в (4), а также условиям (6), (7). Неизвестные коэффициенты А_о, А_и, D_n, фигурирующие в функции тока, необходимо найти из оставшихся соотношений в (3)-(5). Второе условие в (3) на стенке канала приводит к соотношениям

4 (-1)" ^ ^(1-е_п)²А_п «зцо^ н + о²

1 1 _х '

Ао ^{= —}2  ~        ^п) ^^Т11 ^^т

П=1

Оставшиеся условия при ж = а, первое в (4) и второе в (5), дают:

ОО                                             ОО

)+22(-1№-ш = о, о<_У<ь,

^^ + 22 ^sin(ct„?/)A_n(l - е² + 4аа_пе_п

П=1                                П=1

(Ю)

^2sin(a_ny)(-2a^)(l - е_п)³А_п = О, b < у < 1.

П=1

Далее подставляем выражения (9) в (10) и получившуюся систему на коэффициенты А_п решаем приближенно, ограничивая бесконечные ряды N членами. Применим метод коллокаций, для этого разбиваем отрезок [0,1] правой границы (ж = а) N равноотстоящими друг от друга точками у^ и вводим целое число М = [W], Требуем выполнения соотношений (10) только в точках разбиения, получаем систему из N линейных алгебраических уравнений относительно неизвестных А_п (п=1,...,М)

N                                 N                             -

1Ы +    8ш(а_п^)А_п(1 - е² + 4аа_пе_п) + ^С^-1)"^^^) = 0, г = 1,..., М,

П=1                                 П=1

N

^ 8ш(а_п^)(-2о£)(1 - е^² А_п = 0, г = М + 1,..., N.

П=1

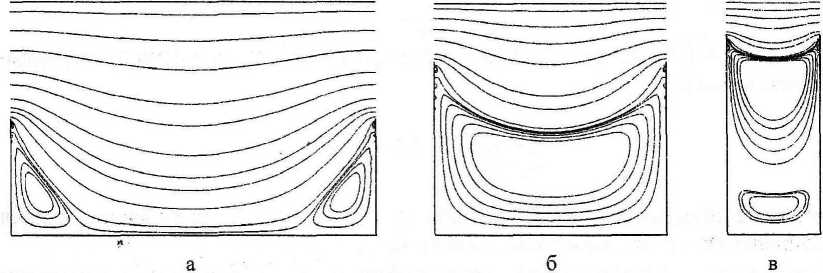
Рис. 2. Линии тока для некоторых конфигураций канала с ребрами:

(а) а = 0,8, 6 = 0,5; (б) а = 0,5, 6 = 0,75; (в) а = 0,2, 6 = 0,85

Вычисление коэффициентов A_n, D_n и нахождение функции тока производилось с помощью пакета символьной математики Maple 8. Характерные картины линий тока жидкости для некоторых вариантов расположения и высоты ребер представлены на рис. 2, расчеты соответствуют разбиению N = 40.

При уменьшении зазора между ребрами и увеличении их высоты (увеличении «шероховатости» канала) картина течения качественно меняется. При достаточно больших расстояниях между ребрами и малых высотах ребер (рис. 2а) циркуляционные течения возникают только в малых областях примыкания ребер к стенкам канала. При уменьшении расстояния между ребрами «угловые вихри» соединяются в одно циркуляционное течение (рис. 26), подобно задаче об обтекании каверны [2]. При увеличении высоты ребер появляются вторичные «вихри» (рис. 2в).

3.    Сила сопротивления

Зная функцию тока в каждой точке рассматриваемой области, несложно получить и распределение давления в канале. Поскольку рж = (Д^)у> ру = —(Д^)х, то, полагая р(0, у) = 0, получаем р(х, у) = ^(ж, у) + f фууу(£, у) d^. о

Сила сопротивления (обезразмеренная на p,QY приходящаяся на один период канала, равна сумме, проинтегрированных по соответствующим площадкам, нормальных напряжений-по ребрам (ж = —а) и (д = а) и касательного напряжения на нижней стенке (у = 0, —а < х < а) [2]

У(-р(-а, у) + 2^у(-а, y^dy + У(р(а, у) - 2^_у(а, y^dy +

Фу^х, 0) dx.

Из условий прилипания на ребрах (4) следует ^^—a/y) = -фх^а^у^ = 0 (при 0 <  у < Ь\ Учитывая нечетность функции давления р(х,у) и четность ^_та(д,у) по х, выражение для силы сопротивления будет следующим

Р_х = 2

j ^_у(д,0) dx + 2 J p(a,y)dy.

(Н)

Используя выражение для давления, последнее равенство несложными преобразованиями приводится к виду

Рх =2

У ^_уу(д, b) dx.

То есть расчет силы сопротивления трения жидкости в канале с ребрами сводится к интегрированию касательного напряжения на уровне у = Ь.

Сравним силы сопротивления, действующие на равные по длине фрагменты оребренного и гладкого каналов. Сопротивление площадки (x,z) Е (—а, а) х (0,1) гладкого канала равно QapQ/H² [2] (в безразмерном виде 6а). Обозначим отношение этих сил сопротивлений

Расчеты коэффициента Ср для течений, изображенных на рис. 2а, б, в, показывают, что при уменьшении расстояния между ребрами и увеличении высоты ребер сопротивление канала увеличивается, и коэффициент увеличения сопротивления соответственно равен Ср = 1,73; 5,25; 16,63. При уменьшении высоты ребер (5 —» 0), как и ожидалось, коэффициент Ср —> 1 и задача переходит в классическое течение Пуазейля [2].

Заключение

В работе решена задача о медленном стационарном течении вязкой несжимаемой жидкости в плоском канале с оребренными стенками. Отметим, что задачу о движении жидкости в канале с периодическим расположением ребер, не ортогональным по отношению к направлению потока, можно получить как суперпозицию задач о течении поперек и вдоль ребер. Поле скоростей последнего течения находится без особых трудностей и вместе с полученным в данной работе решением дает общее решение задачи о косом обтекании жидкостью ребер в канале.

Результаты рассмотренной задачи могут быть использованы для моделирования пористой границы, как это делалось в работах [3], [4]. Усредненное по периоду канала на уровне края ребер значение продольной скорости может выступать хорошим приближением для скорости скольжения на границе «жидкость — пористая среда».