Механические и фрикционные свойства биоэластомеров. Часть 1: описание релаксационных зависимостей кожи человека при растяжении

Природные эластомеры (биоэластомеры) весьма интересны как объект изучения в медико-биологическом отношении (например, в пластической хирургии), а кроме того, необходимы в целях создания функциональных материалов, имитирующих мышцы, кожу, сосуды и другие мягкие ткани. В частности, анализ напряженно-деформированного состояния и трения кожи человека позволяет описывать и прогнозировать эффективность и безопасность процедур пластической хирургии при типичных воздействиях (растяжении, стягивании швом и сдавливании бандажами, а также вибромеханической стимуляции). На основе ранее проведенных исследований [5–7, 9] показана возможность рассмотрения кожи как изотропного несжимаемого нелинейного вязкоупругого материала, для которого связь компонент тензоров напряжений и деформации определяется через удельную потенциальную энергию деформации (упругий потенциал) w :

T x = d W а с ^,

P = T ^x^V R , T = V R ■ P ,

где T ^x - второй тензор напряжений Пиола-Кирхгоффа; C - тензор деформации Коши-Грина; P – тензор напряжений Пиола, определяемый в отсчетной конфигурации; T – 0

тензор напряжений Коши; V R - тензор-градиент вектора места [4]. Несмотря на выраженный нелинейный характер деформирования мягких биотканей типа кожи, для описания их вязкоупругого поведения может быть использовано относительно простое (двух- или четырехпараметрическое) ядро релаксации [6, 7, 9].

В настоящее время для анализа деформирования кожи человека общепризнанным считается использование упругого потенциала Муни–Ривлина или Трелоара [5–7, 9]. Однако в работах [5–7, 9], посвященных биомеханическому моделированию кожи, нет сопоставления результатов использования потенциала Муни–Ривлина с данными, полученными на основе более сложных потенциалов [2]. Это не позволяет сделать однозначный вывод о том, что потенциал Муни–Ривлина является оптимальным с точки зрения адекватного описания процесса деформирования кожного покрова человека.

Целью настоящей работы является совершенствование математической модели деформирования кожи для уточненного описания ее напряженно-деформированного состояния.

Математическая модель

Для несжимаемого материала не все компоненты тензора деформации C являются независимыми. В этом случае при определении компонент второго тензора напряжений Пиола–Кирхгоффа вместо соотношения (1) удобнее использовать выражение, полученное в [4]:

T y =- p G ^{- 1} + 2

^ d w    dw

+

Id 1 1    1 5 1 2 J

E -^W G d 1 2

где T ^y – второй тензор напряжений Пиола–Кирхгоффа для упругого материала без учета вязкости; G – мера деформации Коши–Грина; E – единичный тензор; p – давление, обеспечивающее при произвольном напряженном состоянии выполнение условия несжимаемости материала; w – удельная потенциальная энергия деформации (упругий потенциал); I 1 , I 2 – инварианты меры Коши–Грина.

Наряду с потенциалом Муни-Ривлина w = C ( 1 1 - 3) + C 2 ( 1 2 - 3) в последнее время для описания нелинейного деформирования эластомеров часто используют потенциал Огдена [3, 8]. В упрощенной форме данный потенциал определяется соотношением

W = —2 (x^ + X2 + Xa - 3), a 2

где p, a - параметры упругости материала; X i - главные кратности удлинения. Параметр µ соответствует мгновенному (в момент приложения нагрузки) модулю сдвига материала. Параметр a характеризует степень нелинейности процесса деформирования материала. Потенциал Трелоара [9] является частным случаем потенциала Муни– Ривлина при C 2 = 0 и потенциала Огдена (4) при α = 2.

Для несжимаемого материала независимыми являются только две главные кратности удлинения X i и Х₂ ( X 3 = X -"¹ X" 2¹ ). Независимые кратности удлинения связаны с инвариантами меры Коши–Грина

T — 12 7 2   7 -2 7 -2 T — 7 —2   7 -2 -i- 7 2 7 2

1 1 — X 1 + X 2 + X 1 X 2 , 1 2 — X 1 + X 2 + X 1 X 2 .

Используя потенциал (4) в выражении (3) с учетом (5), для тензора напряжений

T ^y можно получить следующее выражение:

T y — — p G ^{- 1} +---- 2^^[ ( x ^{a+ 2} -X “^{+ 2} ) e + ( x ^a+ ² X ⁴ ₂ -X “^{+ 2} X 4 ) ( I, E - G ) ] .        (6)

a ( X 4 -X⁴₂)^{lv 1       2} /     \ ¹    2     2    1Д ¹ a

Тензор напряжений (6) здесь определен без учета вязкости материала. Для описания вязкоупругого деформирования использовали методику, описанную, в частности, в работах [8, 9]. В соответствии с данной методикой второй тензор напряжений Пиола–Кирхгоффа вязкоупругого материала определяется выражением

t

T ^x ( t ) — T y ( t ) — J T y ( .х )exp ^T 0

— (t — X)

T

dx ,

где 5, т - параметры вязкоупругости. Параметр t соответствует времени релаксации материала, параметр 5 характеризует длительный модуль сдвига р _дл — р (1 — 5 ), а тензор T ^y в (7) задается соотношением (6). Таким образом, функции (6) и (7) определяют связь напряжений и деформаций для рассматриваемого материала – кожи человека. Аналогичная математическая модель использовалась в работе [8] для характеристики механических свойств скелетных мышц. Отличие расчетной методики (6) и (7) от модели, представленной в работе [8], заключается в использовании для тензора T ^y аналитического выражения (6) вместо соотношения (1), поскольку соотношение (1) для несжимаемого материала нуждается в дополнительных уточнениях и трудоемких математических выкладках. Кроме того, приведенное в работе [8] выражение для

T

dw 3 9w  Г t — xЪ

^{T — (1} - ^{5 )} № ⁺⁵ j d C e^XP     T d.

не удовлетворяет условию размерности (второе слагаемое в правой части имеет размерность Па - с).

Идентификация вязкоупругих характеристик

В соответствии с математической моделью, основанной на соотношениях (6) и (7), механическое поведение кожи человека характеризуется четырьмя параметрами: µ, α, δ, τ. Эти характеристики могут быть найдены по результатам стандартных испытаний образцов кожи на растяжение, реализующих одноосное напряженное состояние. Используя функцию (6), для единственной ненулевой компоненты второго тензора Пиола–Кирхгоффа при одноосном напряженном состоянии получим

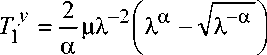
Используя соотношения (7) и (2), для мнимого осевого напряжения получим

о ⁽ t ) ^—

F

S

— X ( t )

t.         ft — х Х

T? ( t ) — 5 f T y ( x ) exp l-- I dx 11

0 v T v

Здесь F – продольная сила, действующая на образец; S – начальная (до начала деформирования) площадь поперечного сечения образца. Функция T ₁ ^y ( t ) в (9) определяется уравнением (8).

Параметры разработанной математической модели δ и τ можно определить независимо от параметров µ и α по экспериментальной зависимости мнимого осевого напряжения от времени в процессе релаксации, когда соотношение (9) примет вид о (t)

, sfl -t 1= 1-5 1 -e т

^о 0

к 7

Здесь сто — начальное (на момент начала процесса релаксации) мнимое осевое напряжение. Функция (10) позволяет определить параметры δ и τ по двум характерным точкам на экспериментальной зависимости о (t). Для этого необходимо измерить напряжение о®, соответствующее завершению процесса релаксации (дальнейшее уменьшение напряжения пренебрежимо мало), и момент времени t0,5, соответствующий напряжению

о 0,5 = 2(о о + о®

) . При

известных о ® и t 0,5 параметры вязкоупругости

определяются по формулам

5 = 1 - ^О ® , т = t о 5 ln 2 . ^о 0

Параметры µ и α предложенной математической модели будем определять по диаграмме растяжения образцов кожи. При заданной скорости растяжения v главная v кратность удлинения X зависит от времени следующим образом: X(t) = 1 + Lt. Здесь L = 100 мм – длина рабочей части образца. Используя данное выражение для λ в формулах (8) и (9), получим расчетную временную зависимость отеор(t) мнимого осевого напряжения при растяжении образца с постоянной скоростью. Произведя замену t = —(X-1), установим расчетную зависимость напряжения от кратности v удлинения отеор(Х). Параметры математической модели ц и а будем выбирать такими, чтобы расчетная зависимость отеор(Х) максимально точно соответствовала экспериментальной диаграмме растяжения оэкс(Х). Используя метод наименьших квадратов [1], будем искать такие µ и α, при которых функция

N

D ⁽ Ц , ^{а )} = ^ [^о экс ^(X i ) ^{- о} теор ^{( X} i ) ] ² i = 1

принимает наименьшее значение. В выражении (12) N – число точек на экспериментальной диаграмме растяжения. В свою очередь, минимизация функции (12) сводится к решению системы нелинейных уравнений

D = 0, ® = 0.

дц да

Решение данной системы с учетом (8), (9), (12) осуществлено в программной среде MathCad 2001. В выражении (9) использовались параметры δ и τ, определенные ранее по диаграммам релаксации и формулам (11).

Пример идентификации вязкоупругих характеристик

Изложенная методика идентификации была использована для определения вязкоупругих характеристик кожи области живота. Образцы для испытаний представляли собой прямоугольные лоскуты кожи толщиной 0,5–2,0 мм и шириной 12 мм, взятые от трупов мужчин и женщин в возрасте от 63 до 85 лет не позднее 24 часов после смерти. Длина рабочей части образца составляла 100 мм. Нагружение образцов и построение экспериментальных зависимостей осуществлялось на испытательной машине Instron 5567 в Институте механики металлополимерных систем им. В.А. Белого Национальной академии наук Беларуси.

Испытания на релаксацию проводились при трех значениях начального напряжения (750 кПа, 150 кПа, 50 кПа). Для каждого значения σ 0 получено 10 экспериментальных зависимостей. На рис. 1 представлены усредненные зависимости относительного мнимого напряжения (отношение текущего напряжения σ ( t ) к начальному σ 0 ) от времени.

По формулам (11) для каждого значения σ 0 определяли параметры вязкоупругости δ и τ. Сопоставляя расчетную временную зависимость относительного напряжения (10) с экспериментальными диаграммами релаксации, вычисляли экспериментальные коэффициенты Фишера F экс [1] для каждого значения σ 0 . Коэффициент Фишера определяется как отношение дисперсии адекватности (средний квадрат отклонения расчетного значения напряжения от среднего экспериментального) к дисперсии воспроизводимости (средняя по экспериментальным точкам дисперсия измерения напряжения). Можно отметить (табл. 1), что коэффициент Фишера не превышает 0,03. Данное наблюдение позволяет [1] сделать вывод о правомерности использования аналитического соотношения (10) для описания процесса релаксации.

В табл. 1 также приведены значения параметров δ и τ. Относительная погрешность параметра δ совпадает с относительной статистической погрешностью измерения напряжения σ ∞ , а погрешность времени релаксации – со статистической погрешностью измерения момента времени t 0,5 . При использовании испытательной машины Instron 5567 приборная погрешность пренебрежимо мала (0,5% для силы и 0,3% для момента времени). Как следует из данных табл. 1, диапазоны варьирования параметров δ и τ перекрываются. Расхождение средних значений параметров не превышает наименьшей абсолютной погрешности. Данное наблюдение подтверждает возможность использования для изучаемого эластомера (кожи человека) допущения о независимости параметров ядра релаксации от значений деформации и напряжения. Путем объединения диапазонов варьирования параметров δ и τ для разных напряжений σ 0 определяются независящие от напряжения значения δ с и τ с (см. табл. 1).

Для идентификации параметров µ и α были получены экспериментальные зависимости мнимого осевого напряжения от кратности удлинения образца при двух скоростях растяжения (50 и 250 мм/мин). Для каждой скорости получено по 10 экспериментальных диаграмм. На рис. 2 представлены усредненные зависимости σ экс (λ).

Значения параметров µ и α, полученные в результате минимизации функции (12) для каждой скорости v , приведены в табл. 2. Там же представлены коэффициенты Фишера, вычисленные при сопоставлении расчетной зависимости σ теор ( λ ) с усредненной экспериментальной диаграммой. Если для описания деформирования исследуемого материала используется потенциал Трелоара [6], параметр α равен 2.

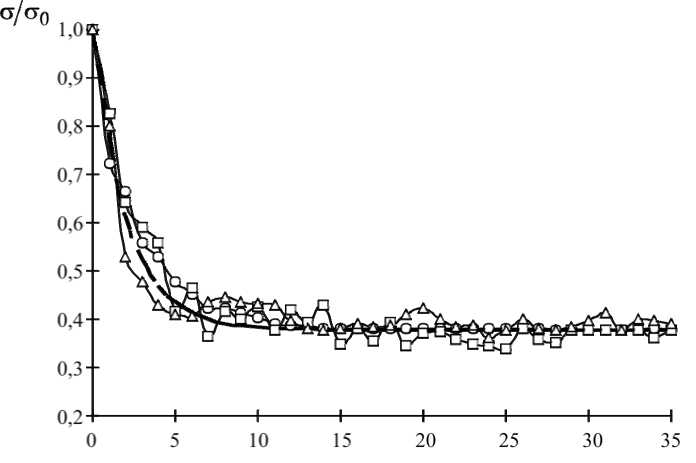
Рис. 1. Зависимость напряжения от времени (релаксация) для кожи. Экспериментальные данные: ○ – при σ 0 = 750 кПа; □ – при σ 0 = 150 кПа; ∆ – при σ 0 = 50 кПа. Пунктирная кривая построена по формуле (10) при значениях параметров δ _c и τ _c (см. табл. 1)

t, с

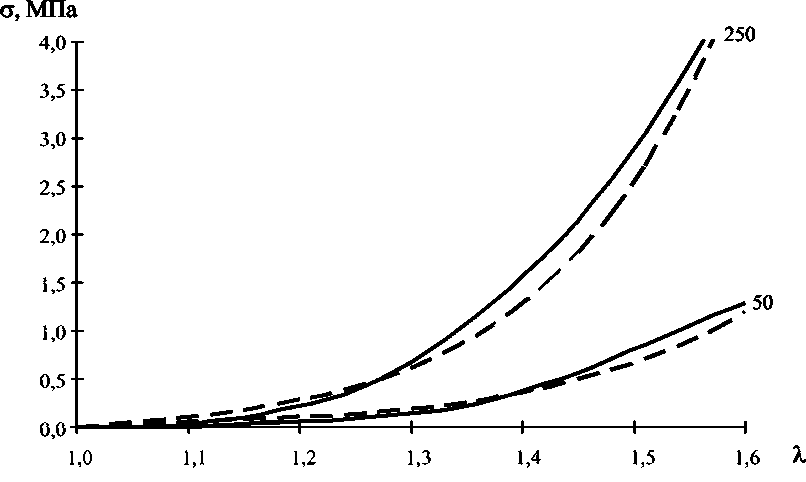
Рис. 2. Диаграммы растяжения кожи. Числа у кривых соответствуют скорости растяжения в мм/мин. Пунктирная кривая построена по формулам (8) и (9) при значениях параметров δ c , τ c (см. табл. 1), µ c , α c (табл. 2)

По диаграмме растяжения определяется только начальный модуль сдвига µ. В табл. 2 в скобках приведены значения µ, полученные в результате минимизации функции (12) при α = 2, а также значения коэффициентов Фишера для расчетных зависимостей σ теор ( λ ), полученных при использовании потенциала Трелоара.

Данные табл. 2 позволяют сделать вывод о том, что математическая модель, основанная на использовании потенциала Огдена, с приемлемой ( F экс < 0,03) точностью описывает процесс деформирования кожи человека в одноосном напряженном состоянии. При использовании потенциала Трелоара погрешность прогноза

Таблица 1

Идентификация параметров модели по диаграмме релаксации

σ 0 , кПа	F экс	δ	τ, мс	δ c	τ c , мс
50	0,011	0,61 ± 0,10	1,93 ± 0,42	0,61 ± 0,10	1,94 ± 0,45
150	0,023	0,59 ± 0,09	1,77 ± 0,28
750	0,009	0,62 ± 0,04	2,06 ± 0,33

Таблица 2

Идентификация параметров модели по диаграмме растяжения

v, мм/мин F экс µ, кПа α µс, кПа αс 50 0,015 (0,981) 342,61±54,46 (8205±1304) 12,42±1,97 337,54±64,11 11,86±2,53 250 0,024 (1,321) 337,54±64,11 (6018±1143) 11,52±2,19 напряжений в образце значительно (более чем в 50 раз) превышает погрешность при использовании потенциала Огдена. Относительная погрешность определения параметров µ и α принята равной средней (по N = 200 точкам экспериментальной диаграммы растяжения) относительной погрешности измерения напряжений. Из табл. 2 следует, что диапазоны варьирования параметров математической модели, определенных при различных скоростях растяжения, перекрываются. Данное обстоятельство позволяет объединить диапазоны варьирования параметров µ и α для различных скоростей v и определить независящие от скорости деформирования значения µс и αс (см. табл. 2).

Заключение

• 1.    В результате сопоставления расчетных и экспериментальных диаграмм растяжения и релаксации образцов кожи в области живота установлено, что совместное использование упругого потенциала и простого экспоненциального ядра релаксации позволяет с приемлемой точностью описать процессы деформирования исследуемой биоткани.

• 2.    Показана правомерность допущения о независимости параметров ядра релаксации от значений деформации и напряжения.

• 3.    Потенциал Огдена обеспечивает более точные расчетные оценки напряжений в образце, чем широко используемый в настоящее время для характеризации механического поведения кожи потенциал Трелоара.