Механические модели аппланационной тонометрии с учетом многослойности роговицы

Определение внутриглазного давления имеет большое значение при диагностике различных заболеваний глаза. Измерение внутриглазного давления производится путем регистрации деформации роговицы в ответ на механическое воздействие. Большинство применяемых методов измерения внутриглазного давления основано на принципе аппланации (тонометр Маклакова, Гольдмана) или импрессии (тонометр Шиотца) (рис. 1).

При аппланационном методе измерения внутриглазного давления роговица деформируется грузом с плоским основанием. По диаметру образованной зоны контакта (тонометр Маклакова) или по величине нагрузки при заданной зоне

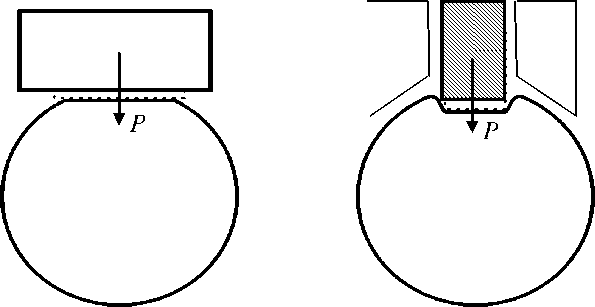
а                              б

Рис. 1. Деформация роговой оболочки при тонометрии: а – аппланационной, б – импрессионной

Карамшина Людмила Александровна, аспирант кафедры теоретической и прикладной механики, Санкт-Петербург контакта груза и роговицы (тонометр Гольдмана) определяют внутриглазное давление с помощью специальных таблиц, которые прилагаются к приборам. Тонометры Гольдмана и Маклакова могут быть описаны одной математической моделью.

При измерении внутриглазного давления тонометрами происходит нагружение наружной оболочки глаза и, как следствие, повышение давления. Это давление, фиксируемое тонометром, получило название «тонометрического». Реальное давление (до нагружении роговицы) называется истинным.

Одна из математических моделей измерения внутриглазного давления по тонометру Маклакова была представлена в работе [2]. Корнеосклеральная оболочка глаза моделировалась двумя сферическими сегментами. Роговица рассматривалась как мягкая оболочка (не сопротивляющаяся изгибным деформациям). При принятых предположениях деформация части оболочки, моделирующей роговицу, описывалась, как и предполагалось первоначально в аппланационной тонометрии, соотношением p t = W / S , где p t – тонометрическое внутриглазное давление, W – вес тонометра, S – площадь контакта. Последнее соотношение справедливо только для бесконечно тонких, мягких оболочек.

Расчеты, проведенные в [2] при различных параметрах роговицы и склеры, дают результаты, которые хорошо согласуются с данными, представленными в калибровочных таблицах [6], и слабо зависят от геометрических и механических параметров оболочек глаза. Однако представленная в [2] модель не может объяснить высокую чувствительность тонометра Гольдмана к значению толщины роговицы в центральной зоне и влияние параметров рефракционных операций на показатели внутриглазного давления [8], так как рассматривает роговицу как абсолютно мягкую оболочку. В связи с этим в работе [1] было выполнено конечно-элементное моделирование задачи в программном пакете Аnsys . Упругая система роговица–склера моделировалась двумя трансверсально-изотропными сферическими оболочками с разными диаметрами и разными упругими свойствами, модуль упругости в направлении толщины обеих оболочек принимался существенно меньшим, чем модуль упругости в тангенциальном направлении. Расчеты, проведенные в [1], показали существенное влияние толщины роговицы на изгибные деформации оболочки. Отмечено, что чем меньше зона контакта груза и оболочки (за счет величины груза или высокого внутреннего давления), тем больше доля усилий, идущих на изгибные деформации.

В данной работе представлено конечно-элементное моделирование аналогичной задачи в программном пакете Аnsys с учетом многослойности роговицы. Исследуется зависимость диаметра площади контакта груза и роговицы (или нагрузки при заданной зоне контакта) от упругих свойств ее слоев и сопряженной с ней склеры при одном и том же внутриглазном давлении. Полученные результаты сравниваются с результатами, полученными при таком же истинном давлении, но для однородной роговицы с осредненным значением упругих свойств составляющих ее слоев.

Некоторые сведения о строении склеры и роговицы

Согласно анатомическому строению глаза склера и роговица имеют форму сферических сегментов разного радиуса.

Экспериментальные исследования свидетельствуют о том, что материал роговицы, как и материал склеры, отличается биомеханической анизотропией и неоднородностью. При нагрузке, соответствующей нижней границе нормального внутриглазного давления (10 мм рт. ст.), тангенциальный модуль упругости роговицы составляет 0,34 ÷ 0,54 МПа [5]. Модуль Юнга склеры в направлении толщины составляет в среднем 0,5 МПа, тогда как в тангенциальном направлении этот показатель меняется в пределах 3–40 МП [5].

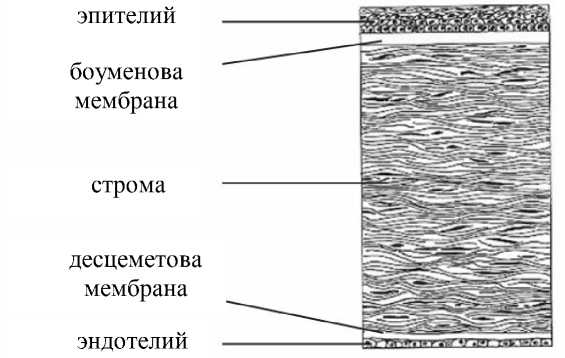
Рис. 2. Структура роговицы

Кроме того, роговица имеет сложную многослойную неоднородную структуру. В роговице выделяют пять основных слоев, которые различаются как по толщине, так и по своей структуре, а, следовательно, обладают различными упругими свойствами (рис. 2).

Эпителий представляет собой наружный мягкий слой роговой оболочки глаза толщиной примерно 10% от всей толщины роговицы.

Основное вещество роговицы на 90% состоит из прозрачной соединительной ткани – стромы. Спереди и сзади к строме прилегают две более жесткие прочные пограничные мембраны – боуменова и десцеметова оболочки толщиной в среднем 12 и 10 мм.

Эндотелий роговицы, задний эпителий роговицы – монослой специализированных плоских клеток, выстилающих заднюю поверхность роговицы, а также всю переднюю камеру глаза. Толщина этого слоя составляет в среднем 10 мкм.

Постановка задачи

Корнеосклеральная оболочка глаза моделируется сопряженными сферическими сегментами с разными диаметрами и разными упругими свойствами (рис. 3). Составная оболочка до нагружения заполнена несжимаемой жидкостью с давлением p (истинное давление).

Диаметр глазного яблока человека варьируется в очень малых пределах и составляет 24 мм. Толщина склеры и роговицы h ≤ 1 мм. Исходя из этих данных (величина h / R << 1) оболочки моделируются тонкостенными (двумерными) упругими оболочками.

Роговица моделируется сегментом меньшего радиуса, который разбивается на четыре слоя (рис. 4): первый (внешний) слой отвечает биомеханическим свойствам эпителия ( L 1 ), второй – боуменовой оболочки ( L 2 ), третий – стромы ( L 3 ), четвертый (внутренний) слой – свойствам десцементовой оболочки ( L 4 ). Склера моделируется однородным сегментом большего радиуса ( L 5 ).

По данным [4, 5], склеру и роговицу можно рассматривать как трансверсальноизотропные оболочки. В связи с этим на упругие коэффициенты оболочек накладывались следующие ограничения [7]:

Ivi| <( EJEf, -1 < Vi < 1 - 2 (V’)2 (E/E), (E,> 0, E,> 0), i = 1,...,5, где Ei и Ei - соответствующие модули упругости при растяжении-сжатии на поверхности изотропии и в направлении, перпендикулярном к ней; vi и vi -коэффициенты Пуассона.

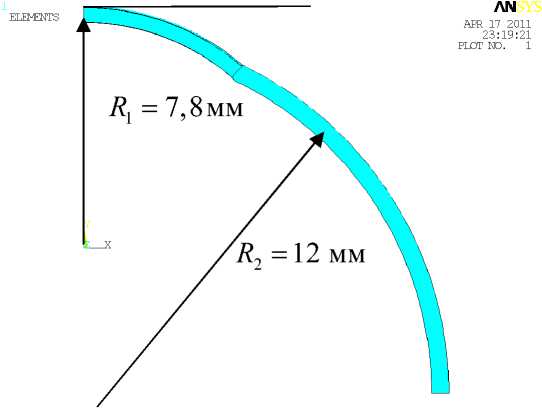
Рис. 3. Склера и роговица моделируются сопряженными оболочками

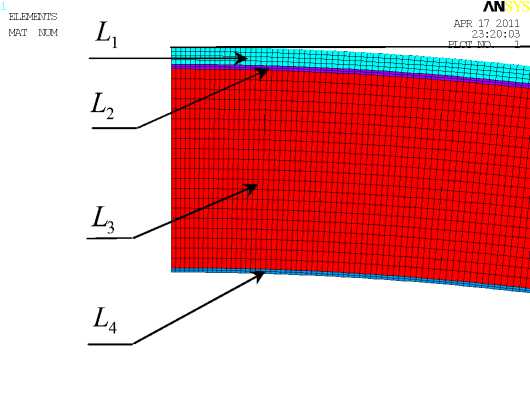
Рис. 4. Материал роговицы разбивается на четыре слоя

Рис. 5. Создание контактной пары «поверхность – поверхность»

Модуль сдвига для поверхности изотропии определяется соотношением G , = E , /2 ( 1 + v , ) .

Предполагается, что роговичная и склеральная ткани близки к несжимаемым, поэтому в расчетах коэффициент Пуассона ( v , ) в тангенциальном направлении принимался равным 0,499.

При измерении внутриглазного давления тонометром Маклакова на роговицу глаза помещается груз с плоским основанием весом 10 г. Под действием груза роговица деформируется, при этом регистрируется диаметр площади контакта груза с роговицей.

Метод Гольдмана основан на измерении силы, которую необходимо приложить для сплющивания фиксированной центральной области роговой оболочки. Сила в (граммах) умножается на десять и полагается внутриглазным давлением. Уплощенная область должна быть диаметром 3,06 мм, так как для этой величины диаметра нагрузка в 0,1 г соответствует внутриглазному давлению в 1 мм рт. ст.

Измерение внутриглазного давления тонометрами Маклакова и Гольдмана моделируется контактными задачами в программном пакете Ansys (рис. 5). На первом шаге прикладывается внутреннее давление, на втором шаге прикладывается сила F = mg , где m – масса груза, g – ускорение свободного давления. В первой задаче к штампу прикладывалась сила, равная 10 г (0,1 H), и фиксировалась площадка контакта. Во второй задаче величина силы давления груза варьировалась таким образом, чтобы зона контакта составляла 3,06 мм.

Для каждой серии расчетов проводится сравнение результатов с расчетом, проведенным для однородной роговицы с осредненными значениями упругих параметров составляющих ее слоев. Осредненные значения модулей упругости для всей роговицы в тангенциальном направлении E ив направлении толщины E' определяются из соотношений [3]:

E =

( 1 ^{- v}2 )

n

Z h i

i = 1

n

Z i=1

E_ih_i ν _i

^{1 - v 2}

E ' =

n

Z h .

i = 1

( 1 -v' ²

i = 1

EM i - v , '²

i = 1,...,4,

где v , v' - осредненные коэффициенты Пуассона, v=Г   П1

ra - v 2/ ^Z

E i h i

^{1 - v} i ²

, ^E , h v '

^1.' /Z

Ei h

1 - v '²"

Соотношения (1), (2) позволяют оценить влияние многослойного строения роговицы на обобщенные параметры всей роговицы (толщину, модуль упругости и коэффициент Пуассона), следовательно, и на изменение показателей внутриглазного давления.

Результаты расчетов

Чтобы оценить влияние многослойности роговицы на показатели внутриглазного давления, варьировались только упругие параметры ее слоев ( E_i и E ' , i = 1,..., 4), при этом толщина каждого слоя, упругие параметры и толщина склеры оставались неизменными. Проводились осесимметричные нелинейные расчеты для разных упругих параметров роговицы, склеры при разных значениях истинного внутриглазного давления. Для модулей упругости использовались данные, представленные в [4, 5]. Для каждой серии расчетов проводилось сравнение полученных результатов с результатами, полученными для однородной роговицы с осредненными значениями упругих параметров составляющих ее слоев.

На рис. 6, 7 представлены распределения контактных напряжений при измерении внутриглазного давления тонометрами Гольдмана и Маклакова (10 г) для корнеосклеральной оболочки, у которой модули упругости каждого слоя роговицы в направлении толщины оболочки в 20 раз меньше тангенциальных модулей, модули роговицы на порядок меньше, чем модули склеры. Истинное внутреннее давление на представленных рисунках 15 мм рт. ст. Значения упругих коэффициентов роговицы и склеры представлены в таблице.

Значения толщины и упругих коэффициентов основных слоев роговицы и склеры

Параметры	Роговица				Склера
	Эпителий	Боуменова оболочка	Строма	Десцеметова оболочка
i	1	2	3	4	5
hi , мм	0,043	0,012	0,5	0,010	0,6
Ei , МПа	0,06	0,6	0,3	0,9	5,0
E , МПа	0,29949				5,0
E ' / E i = 0,05 МПа	0,003	0,03	0,015	0,045	0,5

б

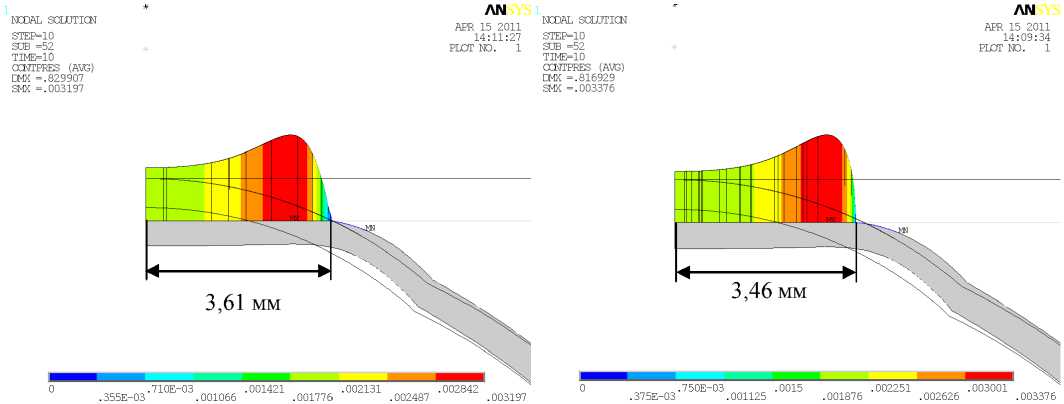
Рис. 6. Распределение контактных напряжений при измерении внутриглазного давления тонометром Маклакова (груз 10 г): а - для многослойной роговицы E / E = 0,05,

= 1,

…, 4; б – для однородной роговицы E = E , = 1,

…, 4, E = 0,2995 МПа и

E' / E = 0,05

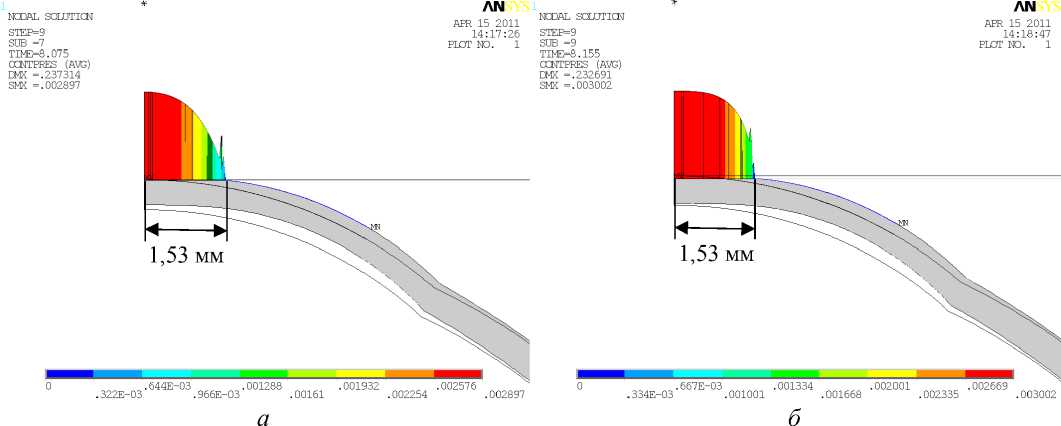
Рис. 7. Распределение контактных напряжений при измерении внутриглазного давления тонометром Гольдмана: а - для многослойной роговицы E ' / E = 0,05, г = 1, „., 4;

б - для однородной роговицы E = E , г = 1, ..., 4, E = 0,2995 МПа и E ' / E = 0,05

На поверхности изотропии коэффициенты Пуассона роговицы и склеры принимались v i = 0,499, i' = 1,..., 5, а в направлении толщины вычислялись согласно соотношениям (1) и (2), и принимались v '= 0,01. Значения для модулей сдвига: G i = 0,9, G' = 0,1, i = 1,...,5.

Выводы

Так как строма составляет 90% всей роговицы, то упругие параметры роговицы как в тангенциальном направлении E и v , так и в направлении толщины E' и v ' в основном определяются упругими параметрами стромы. Вклад более жестких слоев (боуменовой и десцементовой оболочек) в «осредненные» значения упругих параметров целой роговицы за счет их малой толщины оказывается несущественным.

Проведенные расчеты показали, что жесткость этих оболочек оказывает влияние на распределения контактных напряжений и на размеры контактной поверхности.

Сравнение результатов, полученных для тонометра Маклакова (груз 10 г) при многослойной роговице, с результатами, полученными для однородной роговицы, но с осредненными значениями упругих параметров составляющих ее слоев, показало, что зона контакта в первом случае больше, т.е. величина тонометрического давления меньше. Аналогичные результаты получаются для тонометра Гольдмана. В этом случае зоны контакты имеют фиксированное значение 3,06 мм, но величина силы, необходимой для деформации многослойной роговицы с неоднородными по толщине упругими свойствами, меньше, чем величина силы, необходимой для деформации однородной роговицы с «осредненными» упругими свойствами. Таким образом, учет неоднородности по толщине упругих свойств основных слоев роговицы делает более близкими значения тонометрического и истинного внутриглазного давления.

Расчеты, проведенные с учетом многослойности роговицы, так же как и исследования, проведенные в работе [1], показали, что чем меньше зона контакта груза и оболочки, тем больше доля усилий, идущих на изгибные деформации.

В результате моделирования измерения внутриглазного давления тонометром Маклакова, особенно грузом 10 г, отмечается значительное увеличение зоны контакта и влияние склеральной оболочки на процесс деформирования. Так как при измерении внутриглазного давления тонометром Гольдмана диаметр зоны контакта 3,06 мм, а при измерении тонометром Маклакова (5 и 10 г) при «средних» давлениях (от 10 до 30 мм рт. ст.) диаметр зоны контакта больше, то показатели внутриглазного давления при измерении тонометром Гольдмана оказываются существенно более чувствительными к изменению толщины роговицы, чем показатели внутриглазного давления при измерении тонометром Маклакова. Также влияние толщины роговицы на показатели внутриглазного давления при измерении тонометром Маклакова весом 5 г больше, чем на показатели внутриглазного давления при измерении тонометром 10 г, что согласуется и с экспериментальными данными [1].