Механические модели в стабилометрии

Одним из основных инструментов постурологии служит стабилометрическая платформа. Такая платформа имеет датчики силы, которые измеряют только вертикальные компоненты усилий. Вместе с компьютерным комплексом преобразования и обработки сигналов такая платформа образует стабилоанализатор (стабилограф).

Механические модели удержания человеком вертикальной позы строились уже на самых ранних стадиях развития стабилометрии. В литературе известна интерпретация результатов исследования удержания человеком вертикальной позы на основе модели перевернутого маятника [3, 18]. Для описания фронтальных движений корректнее использовать более сложные модели. Обзор различных задач удержания человеком вертикальной позы на основании механических моделей приведен в диссертациях [4] и [14]. Подобные модели используются для обсуждения результатов стабилометрических исследований. Изложение вопроса о связи этих моделей

Кручинин Павел Анатольевич, к.ф.-м.н., доцент кафедры прикладной механики и управления, Москва с показаниями стабилоанализатора часто бывает недостаточно аккуратным и содержит неточности. Необходимую аккуратность выводов позволяет сделать механический анализ, основанный на исследовании физической модели. Подобный анализ частично проведен в статье [16], однако указанная работа практически недоступна и известна в основном по ссылкам. В то же время популярные издания, посвященные анализу стабилометрических исследований [2, 13, 15], не рассматривают этот вопрос, что в ряде случаев затрудняет понимание и интерпретацию результатов стабилометрических исследований. В связи с вышеизложенным представляется полезным подробное изложение и анализ соотношений указанной механической модели.

Не описывая подробно принципов работы стабилометрической платформы, укажем, что основной информацией, которая выдается программным обеспечением стабилоанализатора, являются фронтальная x s и сагиттальная y s координаты точки O n приложения равнодействующей N сил вертикальных реакций, действующих в опорах платформы, а также величина этой равнодействующей.

Рассмотрим описание малых колебаний человека относительно положения равновесия в окрестности вертикальной позы. В этом случае углы отклонения от вертикали сегментов тела человека допустимо считать малыми и рассматривать задачи анализа колебаний в сагиттальной и фронтальной плоскостях раздельно, не учитывая влияния крутильных колебаний вокруг вертикальной оси. Такой подход традиционен и применяется во всех цитируемых в этой статье источниках.

Модель движений в сагиттальной плоскости

Задача описания движений человека в сагиттальной плоскости рассматривалась многократно. Однако при ее анализе часто опускают некоторые особенности, связанные с пренебрежением при моделировании малыми параметрами. В связи с этим обсудим здесь аккуратное обоснование этой традиционной модели.

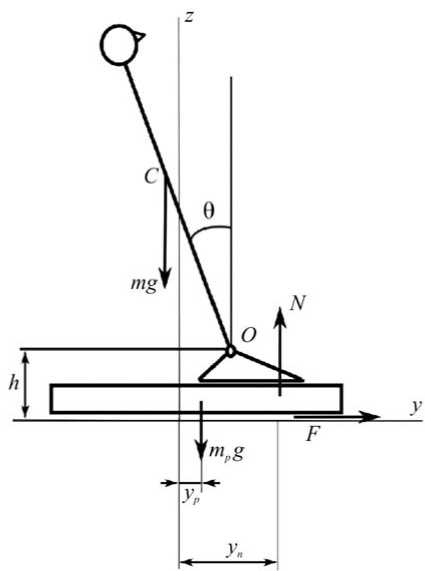
Для описания колебаний человека в сагиттальной плоскости примем традиционную модель перевернутого маятника, изображенную на рис. 1. Традиционно предполагаем, что тело человека в ходе теста допустимо моделировать недеформируемым стержнем массой m , закрепленным шарнирно в точке O , соответствующей голеностопному суставу. В более сложном случае антропоморфного многозвенника такая модель будет описывать наиболее значимую – первую – форму колебаний [9, 14].

Центр масс стержня расположен в точке C , удаленной от точки O на расстояние l_c . Момент инерции стержня относительно фронтальной оси, проходящей через точку О , равен J . Отклонение стержня от вертикали опишем углом θ. Будем считать, что обследуемый ориентирован так, что сагиттальная плоскость человека параллельна оси чувствительности платформы, а его стопа неподвижна относительно платформы.

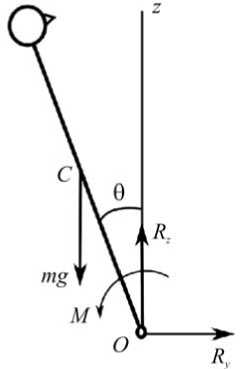
Уравнения движения для малых значений угла θ и скорости его изменения запишем из уравнений плоскопараллельного движения тела [1] в соответствии со схемой рис. 1, б :

ml c ⁹ =- R y ,

< 0 = R z - mg , (1)

_ J 9 = ml c g 9 + M x .

Третье уравнение этой системы полностью описывает движение тела человека и традиционно используется для описания движения:

9 = ml c g 9 + M x . (2)

JJ

а

б

в

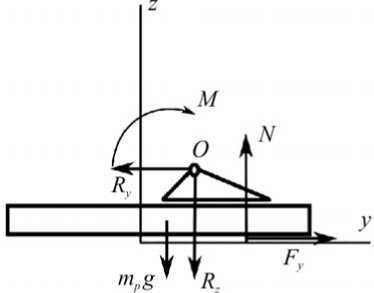
Рис. 1. Модель движений человека в сагиттальной плоскости. Внешние силы, действующие: a – на систему человек – платформа; б – на модель стержня, имитирующего тело человека; в – на систему стопы ног – платформа стабилоанализатора

Для записи соотношений для сагиттальной стабилограммы рассмотрим равновесие системы платформа – стопа под действием силы тяжести m p g этой системы, составляющих N и F y равнодействующей сил в опорах, реакций R y и R z связи в голеностопном суставе и момента M x мышц в голеностопном суставе, приложенных как показано на рис. 1, в .

Уравнения равновесия этой системы имеют вид

[ F y - R y = 0.

• N - R z - m p g = 0,                                    (3)

_ Ny n + F y h ^- M x ^- m p gy p = 0.

где y n – сагиттальная координата центра давления; h – расстояние от точки О до плоскости, образованной чувствительными элементами сенсоров; y p – координата центра масс объединенной системы.

Выражение для измерений стабилоанализатора получим, преобразовав уравнения систем (1) и (3):

Ny n = M x ^- F y h + m p gy p

= M 1 + x

mlch

^^^^^^^e

J

m ² gl_c ² h J

^{9 +} m p gy p •

Для грубой оценки предполагаем, что момент инерции J можно приближенно считать равным моменту инерции стержня длиной 2 l c , что соответствует известным антропометрическим данным [6]:

I 1 3h

Ny„ = Mx 1+ 77

4 l

mgh

-7- ^{9 +} m p gy p •

Таким образом, переменная составляющая сагиттальной стабилограммы совпадает с переменной составляющей величины

s

M x

। m„ mg 1 +— p

m

3 h

4 l

^h l c θ .

m

4 1 + - p l c

m J

c

В этом соотношении l_c θ – расстояние вдоль оси y от оси голеностопного сустава до проекции центра масс человека.

Чтобы сравнить слагаемые в соответствии с теорией размерностей [8, 12],

M приведем это соотношение к безразмерному виду, перейдя к переменным 5 M = —— , M x *

y θ

5 y = — и 59 = —. В качестве характерных значений 9 * , у* и M * примем величину y _*             θ _*

амплитуды изменения угла θ, отклонение y* центра давления и модуль момента в голеностопном суставе при равновесии системы 9 = 9*:

= l c 9 * и M * = mgl c 9 * .

Для этих переменных выражение (4) примет вид

3 h

1+

4 l

5у =----- m

• 1    + - p m

5 M, - x

h

c

m

• 4 1 +

V m )

δθ.

Учитывая соотношения, бесспорно выполняющиеся для взрослых обследуемых, mp       h

—- << 1 и — << 1 и отбросив постоянные слагаемые, получим основное соотношение m          lc переменной составляющей сагиттальной

5у = 5Mx, которое для размерной стабилограммы эквивалентно выражению

A y

A M x

,

mg где AMx - изменение момента в голеностопном суставе.

^mp h

Это соотношение выполняется с погрешностью порядка max < —-, — > для m L

c

любых по темпу движений. Таким образом, сагиттальная стабилограмма в большей степени описывает нормированное изменение момента в голеностопном суставе. Погрешность этого представления для человека среднего телосложения не превышает 10%.

Модель движений во фронтальной плоскости

Как отмечалось еще в работе [3], простая модель перевернутого маятника не описывает полностью удержание человеком вертикальной позы во фронтальной плоскости. Наличие двух опор во фронтальной плоскости и незначительные величины фронтальных моментов, развиваемых мышцами в голеностопном суставе, существенно меняют механическую схему, которую необходимо использовать при моделировании движения. Эта схема зависит от постановки ног [4, 5]. При постановке единственной ноги на платформу стабилоанализатора изменение фронтальной стабилограммы, аналогично модели измерений в сагиттальной плоскости, описывает фронтальный момент в голеностопном суставе [4].

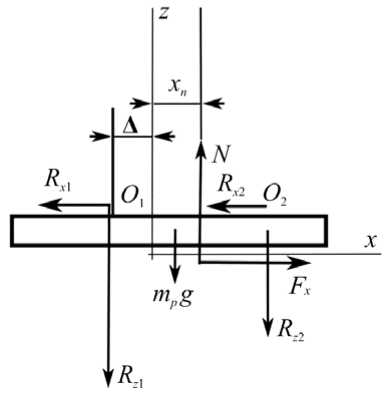
При установке обеих ног на платформу стабилоанализатора задача существенно усложняется. Для упрощения рассмотрим только один случай движения человека, когда ступни располагаются под тазобедренными суставами. Будем считать, что опора ноги о плоскость точечная и центры тазобедренных суставов A 1 , A 2 и точки опоры ног О 1 , О 2 образуют параллелограмм, как показано на рис. 2. Такое положение приближенно соответствует позе «ноги на ширине плеч».

Пусть M1 и М2 – моменты, создаваемые мышцами в правом и левом голеностопных суставах соответственно; l – «длина ноги» OiAi; mb – масса туловища с головой и руками; mf – масса одной ноги, т.е. масса человека m = mb + 2mf.

Примем гипотезу из работы [4] о том, что удержание позы во фронтальной плоскости осуществляется за счет мышц тазобедренного сустава. В качестве обобщенной координаты выберем угол φ, образованный ногой O i A i с вертикалью.

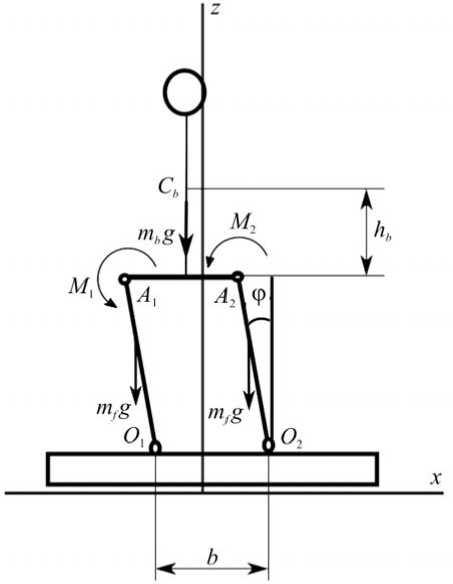
б

а

Рис. 2. Модель движений человека во фронтальной плоскости. Активные силы, действующие в системе человек – платформа ( a ), и внешние силы, действующие на платформу стабилоанализатора ( б )

Уравнения движения такой системы запишем с помощью уравнения Лагранжа [1]. Кинетическая энергия системы имеет вид

T = 2 JJL + ml, 22

где J f – момент инерции ноги относительно сагиттальной оси, проходящей через точку O i , а v b – скорость центра масс «туловища».

Используем для вычисления моментов инерции J f соотношения для моментов инерции стержня. Тогда для малых значений угла φ

T = | m f + m b 1 ²ф². I 3 2 J

Обобщенную силу в этих же предположениях запишем в виде

Q = ( m_b + m_f ) gl ф + M 1 + M2.

Тогда уравнение движения системы с использованием уравнения Лагранжа запишем в виде

Ф =

m     g ф ₊

2l mb + 3 mf

M 1 + M ₂

Ё2 m b ⁺ 3 m f 1 ¹

Это уравнение приближенно описывает движение стоящего человека во фронтальной плоскости и имеет тот же вид, что и уравнение (2), описывающее движение в сагиттальной плоскости.

Для выражения фронтальной составляющей стабилограммы потребуются данные о горизонтальных R_{x 1} , R_{x 2} и вертикальных R_{z 1} , R_{z 2} составляющих реакции опорной поверхности. Для их отыскания воспользуемся теоремой о движении центра масс системы, показанной на рис. 2, a , в проекциях на горизонтальную и вертикальную оси:

^mf v 1 ⁺ m f v2 ⁺ mbV b = - ^Rx 1 - ^Rx 2 ,

0 = Rz 1 + Rz2 -(mb + 2mf ) g, и теоремой об изменении кинетического момента [1] этой системы относительно точки O1:

^d^ ( Kb + Kf i + Kf 2 ) = ^ Mmg + ^ Mr , где v1 и v2 – горизонтальные составляющие скорости центров масс ног; vb – скорость поступательного движения, совершаемого туловищем; Kb, Kf1, Kf2 – кинетические моменты каждого из тел системы относительно фронтальной оси, проходящей через точку O1; E Mmg, E mr - суммы моментов сил тяжести и реакций связей относительно фронтальной оси, проходящей через точку O1.

С учетом малости угла φ, скорости и ускорения его изменения запишем эти соотношения в линеаризованном виде:

( m b + m f ) l ф = ^- R x 1 ^- R x 2 ,

■ ⁰ = ^Rz 1 + ^Rz 2 - ( m b + ² m f ) g ,

2 ,A mb (l + hb) + 3 mfl 1lФ = — (mb + 2 mf) gb + (mb + mf) glФ + 2 Rz 2 b, где hb

высота центра масс «туловища» над тазобедренными суставами; b – расстояние O1O2.

Из двух последних уравнений системы (8) и уравнения (7) выразим вертикальные реакции опорных поверхностей в виде

( m b + ² m f ) g   ф A              2    ,2 Az        x g/ ф

R, = --------------mJ (l + h,) +—mJ +(m, + mf\---, z 1          2          2 b ( b b 3 f J b f) 2 b

( m b + ² m f ) g ф A            2 _a Az         \gl ф

R.^ = ---------- —I-- mJ ( l + h ) + — mJ -I m_h + m_f)--- .

z 2          2         2 b (               3 ^f J ^V b ^f’ 2 b

Показания стабилоанализатора выразим из этих реакций, рассматривая уравнения равновесия платформы для схемы, представленной на рис. 2, б , так же, как и для сагиттальных колебаний

Уравнения равновесия имеют вид

' F x - R x 1 - R x 2 = 0,

< N - R_z 1 - R z 2 - m p g = 0,                                        (10)

Nx + Fh - R Д- R ?(A + 2 b)-m gx = 0, n x p      z 1         z2                    pO p , где xn – фронтальная координата центра давления; Fx – проекция реакций опор платформы на горизонтальную ось фронтальной плоскости; hp – расстояние от точки Оi до плоскости, образованной чувствительными элементами сенсоров платформы; Δ – фронтальная координата точки O1 в осях стабилоанализатора (на рис. 2, б изображено отрицательное значение параметра Δ).

Используем эти соотношения и выражения (8)–(9) для того, чтобы получить выражение для измерений стабилоанализатора в виде

Nxn =( mb + 2 mf) g (b + A) + mpgxp-(mb + mf) gl Ф + mb ( b + hp ) + 3 mfl + ( mb + mf ) hp lФ •

Выразим угловое ускорение из (7) и нормальную реакцию с помощью вторых уравнений систем (8) и (10), а также используем соотношение для масс (6). Отбросив постоянные слагаемые, получим соотношение для величины x s , изменение которой описывает переменную составляющую фронтальной стабилограммы:

xs

mlg

A M h

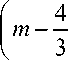
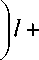
( m - 2 m f ) h_b + ( m - m f ) h_p

m — m

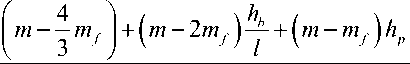
m — m

- 1

A

1 -

^mf "

m v

l φ,

где A M -

–

изменение суммарного момента в тазобедренных суставах,

а

mf

1-- — l ф - фронтальное перемещение центра масс.

m )

Выражение (11) для

фронтальной составляющей содержит «хороший» малый

hp параметр —p«1 и

mf отношение *0,2, которое также в первом приближении m

можно считать малым.

h

Пренебрегая этими величинами и учитывая, что -р <  0,5, получим грубую оценку для

величины x s в виде

AM. L - | , xs *  1 1 + 1 + hb ф .

mg V l J

Чтобы сравнить слагаемые в соответствии с теорией размерностей [8, 12],

A M приведем это соотношение к безразмерному виду, перейдя к переменным о M =---- ,

M _*

5 x s = -xs- и 5ф = —. В качестве характерных значений ф * и M * примем величину l φ _*            φ _*

амплитуды изменения угла φ и модуль момента в тазобедренном суставе, которое обеспечивает равновесие системы при ф = ф * .

M * = ( m - m_f ) gl ф * * mgl ф * .

Для этих переменных выражение (12) примет вид

( кА к

5 x * 5 M I 1 + h b | + h b 5ф .

s I l l

h

Поскольку b- <  0,5, вклад изменения момента в тазобедренном суставе по крайней мере втрое превышает вклад прочих факторов. Таким образом, и фронтальную координату центра давления также можно использовать для грубой оценки изменений момента в тазобедренном суставе.

Обсуждение

Итак, в силу принятых предположений колебания во фронтальном и сагиттальном направлениях управляются группами мышц тазобедренного и голеностопного суставов соответственно.

Несмотря на значительные различия в структуре механической схемы для сагиттальных и фронтальных движений, приближенные уравнения (2) и (7), описывающие эти движения, однотипны. Постоянные времени для этих уравнений

имеют вид

T = 1-^- и T =А s 3g f

m b ⁺ 3 m f l m b + m f g

.

В соответствии с данными [6] для человека ростом 1,7 м эти постоянные времени близки по величине и приближенно составляют 0,16 и 0,2 с. Таким образом, уравнения, описывающие удержание человеком вертикальной позы, совпадают с уравнениями колебаний активно стабилизируемого перевернутого маятника с небольшой асимметрией свойств во фронтальном и сагиттальном направлениях.

Соотношения (4) и (11) для изменения сагиттальной и фронтальной стабилограмм совпадают по форме. Однако весовой вклад слагаемых, определяемых положением центра масс и моментом в суставе, в них различен. Если для сагиттальных колебаний показания стабилоанализатора в соответствии с (5) хорошо отображают изменение момента в голеностопном суставе, то для фронтальной плоскости подобное утверждение носит сильно приближенный характер. Тем не менее в первом приближении стабилограмму целесообразно рассматривать как измерение нормированной величины моментов. Погрешности такого представления вряд ли сильно превышают погрешности определения центра масс человека в результате приближенных громоздких процедур, описанных в [17]. Отметим, что приведенная оценка справедлива для произвольных движений человека, в то время как оценки для движения центра масс часто справедливы только для медленных составляющих, характерных для спокойного стояния.

Такой подход позволяет объяснить, например, «ухудшение устойчивости» у некоторых больных в процессе реабилитации и части космонавтов в ходе послеполетной реабилитации (см., например, [10, 11]). С этим же фактором связаны проблемы использования стабилоанализатора при анализе движений [7].

Можно предположить, что такой эффект связан с тем, что в начале реабилитационного периода у указанных пациентов ослаблена мышечная система, а нервная система, хотя тоже возможно «разбалансирована», но адаптируется быстрее и в итоге осуществляет стабилизацию вертикальной позы меньшими усилиями. В ходе реабилитации мышечная система восстанавливается, и пациент может позволить затрачивать большие усилия на стабилизацию вертикальной позы, так как минимизация суммарных моментов в суставах, в соответствии с гипотезой из работы [3], не является главной целью системы управления вертикальной позой человека.

Благодарности

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант 12-01-00839).