Механические свойства сжатого бетона с армированием ограничительной сеткой

Объектом исследования данной работы являются сжатые железобетонные конструкции с косвенным армированием сетками. В мировой практике строительства все больше возводится многоэтажных каркасных зданий с укрупненной сеткой колонн. Вместе с этим существенно возрастают нагрузки на вертикальные несущие конструкции. Актуальным становится повышение эффективности железобетонных колонн. Под эффективностью здесь понимается способность выдерживать максимально большие нагрузки при минимальных размерах поперечного сечения. Из-за повышенной хрупкости и высокой стоимости высокопрочного бетона его использование для этой цели имеет свои ограничения. Одним из наиболее приемлемых способов достижения такой эффективности считается создание объемно-напряженного состояния в бетоне за счет косвенного армирования [1-3]. Косвенное армирование, ограничивая поперечные деформации, повышает прочность и предельную деформативность бетона при сжатии [4-9]. Энергии для разрушения конструкций с косвенным армированием требуется существенно больше по сравнению с обычными железобетонными конструкциями [10-15]. В результате значительно повышается живучесть каркасов зданий и сооружений, что делает их более устойчивыми к прогрессирующему обрушению при землетрясениях, взрывах и других аварийных ситуациях.

Большая часть научных исследований, посвященных разработке методов расчета прочности сжатых элементов с косвенным армированием, базируется на экспериментальных зависимостях [16, 17]. Такие зависимости получены для определенных условий конкретных опытов и поэтому имеют ограниченную область применения. Кроме того, они не всегда верно отражают физическую суть силового сопротивления конструкций и могут приводить к значительным погрешностям в расчетах. Поэтому актуальна разработка универсального метода расчета несущей способности сжатых элементов с косвенным армированием, адекватно учитывающего основные особенности их конструктивного решения и напряженно-деформированного состояния.

В работе [18] показано, что достоверный расчет прочности коротких сжатых элементов с косвенным армированием можно выполнить на базе нелинейной деформационной модели железобетона. В таком расчете используются диаграммы состояния материалов, в частности криволинейные диаграммы деформирования объемно сжатого бетона. В ряде публикаций [19, 20] отмечается, что параметры этой диаграммы, в основном, зависят от координат ее вершины – максимального напряжения и соответствующей деформации. При этом в проанализированных публикациях прочность и деформативность объемно сжатого бетона оцениваются по эмпирическим зависимостям, что существенно снижает область их практического применения.

Предметом исследования являются прочность и деформативность сжатого бетона с косвенным армированием сетками. Целью данного исследования является определение зависимостей, позволяющих наиболее достоверно вычислять координаты вершины криволинейной диаграммы состояния объемно сжатого бетона с косвенным армированием сетками. Для достижения этой цели решались следующие задачи:

• -    краткий анализ известных зависимостей для вычисления прочности и деформативности бетона с косвенным армированием сетками;

• -    выбор формулы для расчета прочности объемно сжатого бетонного ядра;

• -    вывод формулы для вычисления деформации бетонного ядра при максимальном сжимающем напряжении;

• -    сопоставление результатов расчета деформации в вершине диаграммы объемно сжатого бетона по полученной формуле с опубликованными опытными данными.

2    Методы

Для достижения поставленной цели использован аналитический метод. Достоверность полученных зависимостей проверена по результатам сопоставления результатов расчета с известными экспериментальными данными.

В нашей стране в настоящее время для определения прочности R_b3 и деформации е _Ь03 в вершине диаграммы деформирования бетона с косвенным армированием сетками предлагаются следующие формулы:

^Rb3    ^Rb + ^ф • R xy • ^Rs,xy >

^b03   ^b0 + 0.02 • Cred, где Rs,xy - расчетное сопротивление растяжению арматуры сеток косвенного армирования;

R_b - расчетное сопротивление бетона сжатию;

е _Ь0 - деформации неармированного бетона, соответствующие вершине диаграммы сжатия;

ц_ху - коэффициент косвенного армирования сетками;

Ф и a_red - коэффициенты, определяемые по формулам (3) и (4):

0.23 + a_red '

R xy • ^Rs,xy

“red= Rb + 1

В формулу (4) R_s , _xy и R_b подставляют в МПа.

Приведенные выше зависимости получены по результатам экспериментальных исследований Е.А. Чистякова и К.К. Бакирова [1]. Авторы [2, 6, 8, 13, 15, 17], как правило, за основу принимают эмпирические формулы, полученные еще в 1929 г. американскими исследователями Ф. Ричартом, А. Брандцаегом и Р. Брауном и имеющие следующий вид:

^Rb3 — ^Rb + kff br ;

£Ь03

-г ^ь„ (1 ⁺ /с,у.

где о_Ьт - поперечное напряжение сжатия в бетонном ядре в предельном состоянии по способности;

к - эмпирический коэффициент, чаще принимаемый равным 4.1 или 4.0 [13, 20];

к_Е - эмпирический коэффициент, принимаемый разными исследователями в интервале от 17.5 до 20.5 [6].

В ряде более современных исследований [21-24] показано, что данные формулы далеко не всегда имеют приемлемую точность. В работе [25] на базе теоретических исследований академика Н.И. Карпенко выполнена аналитическая оценка влияния бокового давления на прочность бетона. При этом использованы предложения Дж. Мандера по учету влияния неравномерности обжатия бетона из-за дискретного расположения косвенной арматуры. В результате получена зависимость, которую можно представить в следующем виде:

Rb3 - WbRb, где Wb - параметр, определяющий увеличение прочности бетона за счет обжатия боковым давлением оь,ху и вычисляемый по формуле

1 — о

Wb    ,

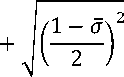
+ m_b

В формуле (8):

m_b - коэффициент материала, устанавливаемый на основании опытов (для тяжелого бетона рекомендуется принимать m_b - 9 , для мелкозернистого бетона - m_b- 7 );

о - относительная величина бокового давления ( о - o_b,_xy/R_b ), которую для конструкций с косвенным армированием сетками предлагается вычислять по формуле:

о-0.5^ь^ ^     ^Rb

,

где ф_ь - коэффициент неравномерности бокового обжатия бетонного ядра (для прямоугольного сечения ф_ь - 0.75 ).

Согласно данным работы [24] лучшую сходимость с данными опытов по определению деформаций в вершине диаграммы состояния объемно сжатого бетона е_Ь03 демонстрирует подход M. Аттарда [21], который предложил использовать следующие зависимости:

(                    ^Ь03 - е^п • £ьо;

)                                     ,    _о х (0.3124+0.0022й_ь)

.

{и - (2.9224 — 0.00408Rb) (0.9^)

Однако следует заметить, что данный подход целиком основывается на результатах статистической обработки опытных данных. Отсутствие физического смысла делает зависимости (10) не очень подходящими для практического применения.

Европейские нормы проектирования (ЕN 1994-1-1. Eurocode 2: Design of Concrete Structures) для расчета деформаций г_Ь03 рекомендуют более простую формулу

ЕЬ03

^- ^ Ь0

(^

Хотя формула (11) менее точна по сравнению (10), она имеет четкое логическое обоснование. Здесь учитывается известный факт того, что рост предельной деформации напрямую связан с ростом прочности бетона. Правда при этом остаются неучтенными такие важные факторы, влияющие на деформативность бетона, как его исходная прочность и начальный модуль упругости.

3    Результаты и обсуждение 3.1    Вывод формулы для определения деформаций объемно сжатого бетона

В этой связи актуальна задача получения новой формулы для расчета е _Ь03 на основе феноменологического подхода. Для чего рассмотрим графические зависимости o_bz - £_bz одноосно и объемно сжатого бетона (рисунок 1). Полную деформацию бетона при любом напряжении для обеих зависимостей можно представить как сумму упругих ( £_el и £'_el ) и неупругих ( е _р1 и е^ ) деформаций.

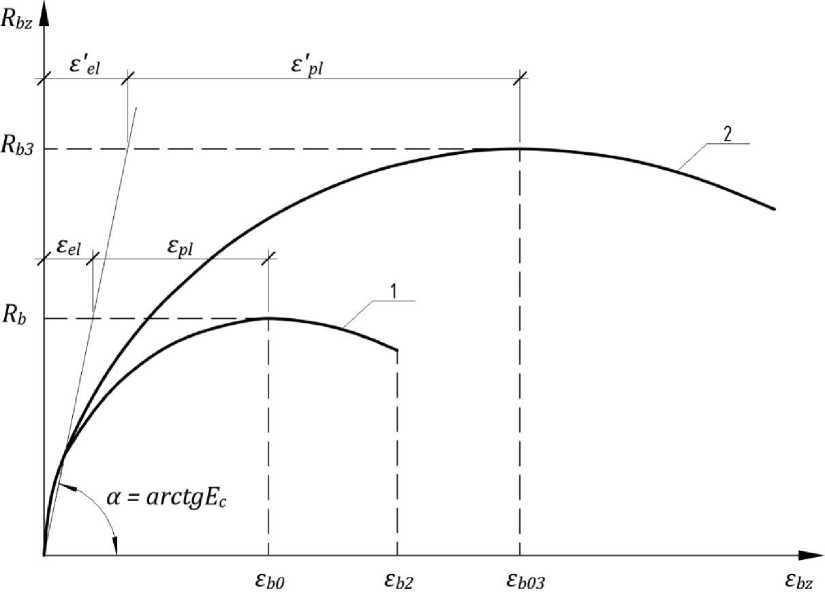
Рис. 1 - Диаграммы деформирования одноосно сжатого (1) и объемно сжатого (2) бетона Fig. 1 - Diagrams of deformation of uniaxially compressed (1) and volumetric compressed (2) concrete

В соответствии с этим запишем

^£b03 = ^£'el + ^£'pl ,                                                 (12)

где е’ _el - упругие деформации объемно сжатого бетона, которые связаны с соответствующими деформациями одноосно сжатого бетона следующей зависимостью:

£'el = £ el ^ 3 .                                              (13)

Rb

Пластические деформации объемно сжатого бетона  е'р1  также можно связать с деформациями ер1 одноосно сжатого бетона. Для этого запишем следующее уравнение:

( R

^£ ьо -"Ё^/ ^Х "                                           ⁽¹⁴⁾

Зависимость (14) показывает, что неупругие деформации при объемном сжатии отличаются от аналогичных деформаций при одноосном сжатии в х раз. Логично предположить, что число х , в основном зависит от соотношения прочностей объемно и одноосно сжатого бетона и определяется по формуле

Х = ^ ь^п .                                             (15)

После подстановки (13), (14), (15) в исходное уравнение (12) и небольших преобразований получаем следующую формулу

^ b03 = ^ b0 • W b" • [1--^(1 - И/ „^М "' )].                          (16)

L     ^£b0 k b

Первоначально было сделано предположение, что показатель степени и в формулах (15) и (16) может быть принят постоянным числом. Статистический анализ показал, что в этом случае лучшему совпадению с экспериментальными данными соответствует значение и * 2.5. Однако дальнейшие расчеты показали, что лучшего совпадения с опытами можно достигнуть, если не принимать показатель степени и постоянным числом. При известной из опытов деформации еЬ03 значение и вычисляется по формуле и =

/и(

^£Ь03 • ^Eb ^{— R}b3 ' ^£Ь0 • Е ь - Rb '

lnWb

После статистической обработки опытных данных выявлено, что на значение и наиболее заметное влияние оказывают два параметра: прочность объемно сжатого бетона и прирост этой прочности за счет косвенного армирования. По результатам двухфакторного анализа опубликованных опытных данных [1, 4, 5, 9], включающих разные варианты геометрических и конструктивных параметров сжатых железобетонных элементов с косвенным армированием сетками, получена следующая зависимость:

и = 8.8 - 1.6W_b - 0.1R_b3 + 0.0007R_b3²,

в которую R_b3 подставляют в МПа.

Графическое представление этой зависимости дано на рисунке 2.

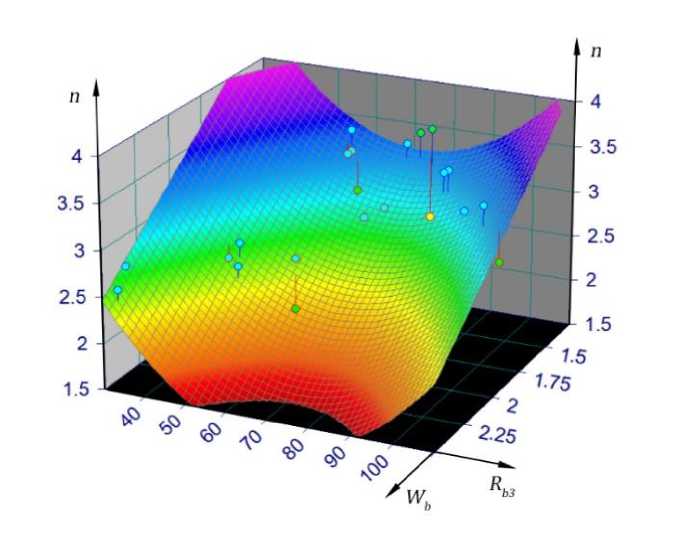
Рис. 2 - Графическое представление статистической зависимости п от R _b3 и W _b Fig. 2 - A graphical representation of the statistical dependence of п on R _b3 and W _b

• 3.2    Сопоставление теории с экспериментом

Очевидно, что формулы (7) – (9), (16) и (18) отражают основные факторы, влияющие на прочность и предельные деформации объемно сжатого бетона. Относительно достоверности предложенных формул можно отметить следующее.

В работе [24] выполнен анализ большого числа зависимостей, предлагаемых для расчета напряжения в вершине диаграммы объемно сжатого бетона. Для верификации данных зависимостей были обработаны существующие экспериментальные данные более 300 сжатых образцов, усиленных сетками косвенного армирования. Показано, что при определении прочности бетона наибольшую достоверность демонстрируют зависимости (7) – (9).

Сопоставление результатов расчета деформации в вершине диаграммы объемно сжатого бетона по формулам (2), (10), (11) и (16) выполнено в таблице 1. Оно свидетельствует о большей точности формулы (16) с переменным значением п , определяемым по формуле (18). При ее использовании получились заметно лучше все сравниваемые показатели статистического анализа: максимальное и минимальное отклонения от опытов (+29/-23%), среднее значение отклонения (1%) и стандартное отклонение (7%).

Таблица 1. Сопоставление данных экспериментальных исследований с результатами расчетов Table 1. Comparison of experimental research data with calculation results

№	Й Ь	М ху	Й5	ЙЬ3	« Ь	с оп гЬ03	оп гЬ03	оп гЬ03	оп гЬ03	оп гЬ03
							теор [2] ЬЬ03	теор[10] ЬЬ03	теор [11] ЬЬ03	теор[16] ЬЬ03
					J.	Henzel [9]
1	13.1	0.0402	575	36.6	2.79	0.01340	1.04	1.36	0.61	1.07
2	23.8	0.0402	575	50.3	2.11	0.00890	0.86	1.16	0.57	1.10
3	30.9	0.0402	575	58.9	1.91	0.00680	0.75	0.97	0.51	0.99
4	13.1	0.0452	575	35.0	2.67	0.01300	0.95	1.22	0.53	1.12
5	23.8	0.0452	575	52.3	2.20	0.00870	0.79	1.06	0.50	1.09
6	30.9	0.0452	575	66.8	2.16	0.00580	0.60	0.78	0.39	0.84
М. Шериф [5]
7	42.7	0.0205	447	76.0	1.78	0.00430	0.88	1.00	0.61	1.07
8	58.0	0.0202	445	83.0	1.43	0.00440	1.07	1.06	0.57	1.10
9	58.0	0.0520	455	98.6	1.70	0.00600	0.95	1.00	0.51	0.99
10	58.0	0.1020	440	119.3	2.06	0.00800	0.71	0.97	0.53	1.12
11	58.0	0.0751	460	89.8	1.55	0.00810	0.95	1.13	0.50	1.09
Е.А. Чистяков, К.К. Бакиров [1]
12	42.0	0.0186	400	59.3	1.41	0.00430	0.93	1.07	0.88	0.99
13	42.0	0.0186	400	58.8	1.40	0.00450	0.98	1.12	0.92	1.03
14	41.2	0.0186	400	59.8	1.45	0.00430	0.93	1.07	0.88	0.98
15	42.2	0.0419	400	65.8	1.56	0.00550	1.20	1.00	0.65	0.99
					Ю.Н	. Карнет [4]
16	56.3	0.0260	300	81.5	1.45	0.00416	1.04	1.05	0.88	1.04
17	53.4	0.0260	300	80.8	1.51	0.00415	1.01	1.04	0.92	1.02
18	58.5	0.0260	300	86.5	1.48	0.00365	0.94	0.92	0.88	0.92
19	46.0	0.0519	300	93.7	2.04	0.00523	0.90	1.00	0.65	0.99
20	57.2	0.0519	300	100.8	1.76	0.00526	1.03	1.04	0.95	1.05
21	58.1	0.0519	300	100.8	1.73	0.00526	1.05	1.05	0.92	1.05
Максимальная величина							1.20	1.36	0.96	1.12

№    Rb    R xy      Rs	Rb3	« ь	c оп bb03	оп bb03	оп bb03	оп bb03	оп bb03
				теор [2] bb03	теор[10] bb03	теор [11] bb03	теор[16] bb03
Минимальная величина				0.60	0.78	0.39	0.84
Среднее значение				0.93	1.05	0.72	1.01
Стандартное отклонение				0.14	0.11	0.17	0.07

Причем, в отличие от формулы (11), формула (16) устанавливает зависимость деформации b_b03 не только от величины прироста прочности бетона при трехосном сжатии, но также от прочности и начального модуля упругости исходного одноосно сжатого бетона. Данное обстоятельство несомненно соответствует физическому смыслу рассматриваемого процесса работы сжатого элемента с косвенным армированием, что и позволило заметно уточнить расчет деформаций.

4    Заключение

• 1.    Предложенные зависимости для определения напряжения и деформации в вершине диаграммы состояния бетона с косвенным армированием сетками обеспечивают более высокую точность, по сравнению с широко используемыми в настоящее время. При их использовании основные показатели статистического анализа результатов сопоставления с данными опытов получаются заметно лучше, чем при расчет по другим известным зависимостям.

• 2.    Выполненное исследование поможет обеспечить большую достоверность деформационному расчету прочности сжатых железобетонных элементов с сетками косвенного армирования.