Механика жидкости в периваскулярном пространстве

Эксперименты Гадашека и соавт. ( Hadaczek et al. ) [9] выявили, что артериальные пульсации играют важную роль в транспортировке молекул лекарственных веществ в мозг при конвекционно-усиленной доставке лекарств ( convection enhanced delivery ). Конвекционно-усиленная доставка – это метод локальной доставки лекарств для лечения неврологических заболеваний [3]. Согласно этому методу лекарства впрыскиваются непосредственно в ткань через иглу или катетер. Гадашек и соавт. ( Hadaczek et al. ) [9] обнаружили, что у крыс без сердечных сокращений наблюдается значительно меньший объем распределения полученных лекарств, чем у живых крыс. Нивс и соавт. ( Neeves et al. ) [16], а также Фоли и соавт. ( Foley et al. ) [7] показали, что наночастицы, добавленные в мозг, двигаются преимущественно через периваскулярное пространство, а не внешнеклеточный матрикс. Главная цель данной работы – исследовать с помощью методов математического моделирования механику жидкости в периваскулярном пространстве, индуцированной перистальтическим движением стенок кровеносных сосудов, и показать его влияние на транспортировку жидкостей и растворов в периваскулярном пространстве.

Течение жидкости, вызванное перистальтикой, активно изучается в литературе. Классический обзор может быть найден в работе [12]. Для математической

Ванг Пенг, аспирант факультета химической и биомолекулярной инженерии, Университет Корнелл, Итака Олбрихт Уильям Л., профессор, кафедра биомедицинской инженерии, Университет Корнелл, Итака формулировки и упрощений большинство исследователей рассматривают перистальтические волны как бесконечный набор синусоид. Если отношение амплитуды волны к полуширине пути прохождения предположить малым, то можно использовать пертурбационные подходы, основанные на разложениях в ряд Тейлора, и можно получить получисленные решения. Если отношение длины волны к полуширине пути прохождения большое, тогда могут применяться теории смазки и при некоторых условиях могут быть получены аналитические решения. Численные методы в исследованиях динамики жидкостей позволили напрямую решать уравнения Навье–Стокса со сложной геометрией границ и граничными условиями (например, сложные формы перистальтических волн [1]). Более того, эти методы позволили лучше понять влияние перистальтики на течение жидкостей. Большое число предыдущих работ было посвящено описанию различных биологических и физиологических процессов. Например, полученная в работе Шапиро и соавт. (Shapiro et al.) [21] математическая модель применялась для описания системы мочеточника и обсуждались физиологические влияния на феномены рефлюкса и запирания жидкости. Мишра (Mishra) и Рао (Rao) [14] предложили подход для моделирования течения жидкости в желудочно-кишечном тракте с учетом изучения перистальтического движения в канале с пористым периферическим слоем. В работе Билстона и соавт. (Bilston et al.) [1] был проведен детализированный численный анализ движения спинномозговой жидкости вдоль периваскулярного пространства в спинном мозге с использованием численных методов. В работе Склея и соавт. (Schley et al.) [20] была построена математическая модель для проверки гипотезы о том, что периваскулярный дренаж интерстициальной жидкости и растворов из тканей мозга был вызван пульсациями стенок кровеносных сосудов. В данной работе предложена новая модель для описания течения жидкости, индуцированного перистальтическим движением стенок кровеносных сосудов в периваскулярном пространстве мозга, и изучены физиологические и терапевтические воздействия на эти движения в рамках метода конвекционно-усиленной доставки лекарств.

Математическая модель

Периваскулярное пространство моделируется как пористая среда, окружающая кровеносный сосуд (рис. 1). Естественно, мы выбираем цилиндрическую систему координат, чтобы ось z совпадала с центральной линией. Поперечное сечение периваскулярного русла является кольцом. Для упрощения математической формулировки задачи сделаем несколько допущений. Внешняя и внутренняя стенки цилиндра считаются непроницаемыми. Внешняя стенка кольца закреплена при r = R 2 , а внутренняя стенка осциллирует по закону

h ( t , z ) = R 1 + b sin

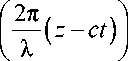
где h ( t , z ) – радиальная координата точки с осевой координатой z на внутренней стенке во время t . Форма колебаний на внутренней стенке представляет собой синусоидальную перистальтическую волну с половиной амплитуды b , длиной волны λ и скоростью волны c , которая двигается по внутренней стенке (чей средний радиус равен R 1 ) в положительном направлении оси z . Частота этой волны равна f = c / λ. Периваскулярное пространство задается как пористая среда с постоянной пористостью ε и проницаемостью κ. Жидкость считается ньютоновской и несжимаемой с постоянной вязкостью µ и плотностью ρ. В табл. 1 приведены основные обозначения, используемые в данной работе. В табл. 2 представлены значения параметров, используемых в данной работе.

В инерциальной системе отсчета, в которой пористая среда движется со скоростью v med , определяющим соотношением является обобщённое уравнение Бринкмана (дополненное уравнение Дарси) [4, 16, 17]

fd v       ^         8Ц

Р I + v - V v I = ^{- V} p ^-    ( v - v med ) .

V d t           )           к

Учитывая, что уравнение (1) справедливо в любой инерциальной системе отсчета (в отличие от оригинального уравнения Бринкмана–Дарси, которое справедливо только в том случае, когда пористая среда неподвижна в выбранной системе отсчета).

Уравнение неразрывности записывается в виде

V - v = 0.

В решении задач, связанных с перистальтикой, удобно применять преобразование координат [21]. Вместо рассмотрения отсчетной конфигурации Σ, в которой пористая среда (периваскулярное пространство) неподвижна, а перистальтическая волна перемещается, перейдём к волновой системе отсчета,

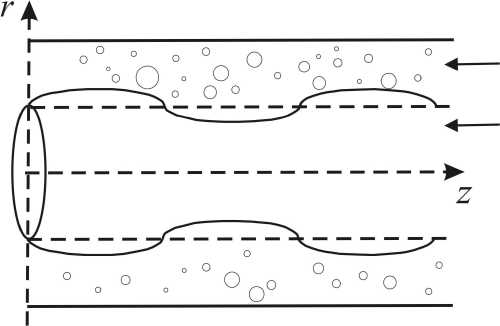
Периваскулярное пространство

Кровеносный сосуд

Рис. 1. Геометрическая область задачи

Таблица 1

Обозначение параметров и переменных

Символ	Физический смысл	Символ	Физический смысл
R 2	Внешний радиус	f	Частота волны
R 1	Средний внутренний радиус	T	Период волны
b	Половина амплитуды	ρ	Плотность жидкости
λ	Длина волны	v	Истинная скорость жидкости (в отличие от скорости поверхности)
c	Скорость волны	p	Давление жидкости
κ	Проницаемость Дарси	ε	Пористость среды
K	Гидравлическая проницаемость (= κ/µ)	h	Радиальная координата внутренней стенки

Таблица 2

Значения параметров, входящих в модель

Параметр	Значение	Ссылка
R 1	1∙10 –5 м	[13]
R 2	1,1∙10 –5 м	[11]
b	5∙10 –7 м 2,5 ∙ 10 –7 м 1,25 ∙ 10 –7 м	[1]
c	1 м∙с –1	[8, 10, 13]
f	5 Гц	[9]
µ	9 ∙ 10 –4 Па∙с	[2]
K	2 ∙ 10 –12 м 4 ∙Н –1 ∙с –1 2 ∙ 10 –11 м 4 ∙Н –1 ∙с –1 2 ∙ 10 –10 м 4 ∙Н –1 ∙с –1	[15, 22]
ε	0,26	[18, 19]

θ'

в которой перистальтическая волна оказывается неподвижной, а пористая среда осуществляет движение. Замена координат – r′ = r, θ′ = θ, z′ = z-ct, t′ = t , а соответствующие замены скоростей – vr = vr, vθ = vθ, v z = vz -c . При переходе к волновой системе отсчета Σ′ появляется преимущество в том, что форма волны

Г 2п ,) внутренней стенке описывается выражением h(t , z ) = R1 + b sin I —z I, которое v ^ / зависит от времени (нет зависимости от t ). Другим преимуществом перехода к является то, что периодическое движение в Σ становится стационарным течением в [21]. Эти два преимущества значительно упрощают задачу.

на

не

Σ′

Σ′

Определяющие соотношения в Σ′ для осесимметричной задачи, для которой ∂ справедливы vθ' = 0 и ∂θ′ = 0, записываются в виде для компоненты r :

ρ

∂v     ∂v vr r +vz r

∂ r      ∂ z

∂p εµ v -;

r ;

∂ r   κ

для компоненты z :

ρ

∂v     ∂v vr z +vz z

∂ r      ∂ z

∂ p εµ εµ c - v -∂ z κ ^z κ

Далее используется теория смазки. Эта теория была впервые предложена для тонкопленочного течения в пустом пространстве (в отличие от пористой среды). ρ c κ            R

Однако можно показать, что при Re =     ≪ 1 и β = ² ≪ 1 , согласно значениям,

µλ           λ взятым из табл. 2, определяющие соотношения могут быть упрощены

^ _ 0, д r'

др! _ _- ^гЦ v- д z’      к ^z '

Уравнение (5) приводится к виду

εµ c κ

.

p ' = p ‘ ( z ') .

Уравнение (6) приводится к виду и к dp' v z ' ( z' )^_-TV^- c . εµ dz

В волновой системе отсчета S' объемная скорость течения жидкости является R 2

постоянной, равной Q' _ J h ( v_z , ■ 2п r'dr' и не зависящей от z [21]. Подставляя (8) в вышеуказанное уравнение и проводя интегрирование, получим

Q _ n [ R 2 - h ² ( z' ) ]

\- _А dp; V гц dz'

)

c

.

dp'

Выразим : dz'

dp'_ гц ----_-- < dz' κ

Q'

. n [ R 2 - h ² ( z' ) ]

+ c

.

Так как h ( z´ ) является периодической функцией от z´ с периодом λ, то из (10) dp'

следует, что    тоже является периодической функцией от z´ с периодом λ. Интеграл dz'

dp'

от --- по z на любом интервале с длиной к должен быть равен Арх вне зависимости dz'                                                                           λ от начальной точки интервала. После некоторых прямых преобразований получим

, 8 С цк ^А p к ^_ — <  κ

Q ' 4π cR ₂ ²

1 - R ¹

Г b

+

R 2 )

V R 2 7

¹ + R ¹

v ^R 2 7

В начальной системе отсчета Σ изменение давления А p _к _ А p{ , а объемная скорость течения за время t через координатой z равна

R 2                          R 2                                1

Q ( t , z ) _ 2п     г vrdr _ 2пг       v ,,( z' ) + c\rdr =—

h ( t , z ) ^z                       h ( t , z ) ^{z '}                                2

где h _ h ( t , z ) _ R 1 + b sin

выражение для Q ( t , z )

r b

- 1

V ^R 2 7

на длине волны равно поперечное сечение с

г Q' + пг c ( R ₂ ² - h ² ) ,

. Подставляя эти соотношения в (11), получим

2πε cR

, 2 Г K\p.

к +1

Q ( t , z ) = в

_V s c цХ    ₇

+ ns c ( R2 - h ² ) .

¹ в R ¹

V R 2 7

Г b

+

V ^R 2 7

¹ + R ¹

V    R 2 7

Г ь

V ^R 2 7

Обозначим среднюю по времени

скорость

течения

1T как Q (z )=-j Q (t, z) dt.

T ₀

После небольших вычислений получим

Q = ns cR 22 <

1 в R ¹

2( в K^ P x

εcµλ

Г ь

+

+ 1

в

( р А

R-

V R 2 7

в

Г ь

² V R 2 7

V ^R 2 7

1 + R L

Г ь

V ^R 2 7

Учтем, что Q является константой, не зависящей от z .

Результаты и обсуждение

На первый взгляд, теория смазки линеаризует определяющие соотношения и стремится решить проблему с помощью принципа суперпозиции, т.е. полная объемная скорость течения является сумной вкладов от градиента давления и перистальтического движения границы. В волновой системе координат Σ’ полученное определяющее соотношение является неоднородным (6), в то время как в начальной системе отсчета граница является подвижной. Эти факты делают принцип суперпозиции неприменимым в любой системе отсчета. Как результат, градиент давления и перистальтическая волна объединены в решении. Чтобы прояснить ситуацию, был рассмотрен особый случай, в котором очень мало. В данном случае были

R 2

использованы разложение в ряд Тейлора относительно правой части уравнения (13) R 2

и аппроксимация результата с сохранением слагаемых до второго порядка: R 2

Q - ns cR 22 <

1 в

IT

V R 2 7

1 + 3 R L

2 1

в

V

. V ^R 2 7 .

( R A

R ¹

V R 2 7

Г ь)

V ^R 2 7

( в K^PX в 1) + 1 в ε c µλ

с р л

V R 2 7

Г b

² V R 2 7

^ . (14)

Уравнение (14) может быть записано в следующем виде:

Q - ns cR 2 <

-

R 1

-

κΔ p _λ

2 R ¹

V

V ^R 2 7

_V s c цХ ₇

+

V ^R 2 7

b

1 + 3 R ¹

-

R 1

V ^R 2 7

+

V ^R 2 7

b

κ ∆ p _λ

V ^R 2 7

2 1

-

R 1

\

_V R 2 ) s c цХ

^ . (15)

V

V ^R 2 7

Первое слагаемое в правой части уравнения (15) зависит от градиента давления (положим b = 0 в (15)). Второе слагаемое зависит от перистальтической волны с очень маленькой амплитудой (положим ∆pλ = 0 в уравнении (13) и разложим выражение в ряд Тейлора относительно ). Третье слагаемое учитывает совместный вклад R2

градиента давления и перистальтической волны. Этот член необязательно является малым по сравнению со вторым слагаемым, так как на величину ∆pλ не накладывались какие-либо ограничения. Однако при условии, что мало, третий член всегда

R 2

меньше по сравнению с первым слагаемым вне зависимости от величины ∆ p _λ .

Интересно сравнить наши результаты с данными, полученными в работе

Билстона и соавт. (Bilston et al.) [1]. В статье было проведено численное моделирование динамики течения жидкости в периваскулярном пространстве спинного мозга. В работе считалось, что периваскулярное пространство в спинном мозге – пустое пространство (в отличие от пористой среды). Из (13) видно, что в нашей модели скорость течения линейно зависит от градиента давления, что также отмечалось в работе [1]. В отсутствие градиента давления и при маленькой амплитуде волны скорость течения

( R 1

равна

V ^R 2 7

Г ь Y

-

( R i

V R 2 7

⋅ π cR ₂² ,

которая пропорциональна скорости распространения

V R 2 7

волны, как было показано в [1]. Однако тот факт, что скорость течения пропорциональна квадрату амплитуды волны, отличается от линейной зависимости, предложенной в работе Билстона и соавт. (Bilston et al.) [1]. В нашей модели учитывается скачок градиента давления, при котором скорость течения падает до нуля. Вычисление критического скачка градиента давления проводилось при b = 1, 25⋅10-7м и K = 2 ⋅10-10 м4 ⋅ Н-1 ⋅ с-1 , взятых из табл. 2. Приравнивая к нулю Q в уравнении (13), можно получить величину градиента давления, равную 9, 4⋅106Па ⋅ м-1 . Большее значение b и/или меньшее значение K дает гораздо большую величину критического градиента давления. В работе Билстона и соавт. (Bilston et al.) [1] эта величина равна 1,4⋅107Па⋅м-1.

В работе Склея и соавт. (Schley et al.) [20] была предложена математическая модель, описывающая обратный периваскулярный транспорт амилоида-β из мозга. В нашей модели может быть показано, что перемещение любой частицы, осредненное по времени, всегда положительно вне зависимости от ее начального положения, тем самым обратный транспорт веществ не учитывается. В нашей модели периваскулярное пространство в мозге моделируется как пористая среда (частично заполненная и поддерживаемая клетками) с заданной шириной 1 мкм [11] (зависящей от размера кровеносного сосуда). Уравнение (1) используется для изучения объемного течения жидкости в этой пористой среде. Течение жидкости в пограничном слое не может быть изучено с помощью уравнения (1), так как в нем не учитывается важное слагаемое (т.е. слагаемое, учитывающее вязкость жидкости) для исследования пограничного слоя [5]. Толщина пограничного слоя порядка κ , которая равна 42 нм при K = 2 ■Ю-12 м4 ■ Н-1 ■ с-1 и 420 нм при K = 2 ЛО-10 м4 ■ Н-1 ■ с-1. Так как толщина слоя сопоставима с размерами пор в среде, то можно смоделировать этот слой как непористую среду и использовать уравнение Навье–Стокса для исследования эффектов в этом слое (что и было сделано в работе Склея и соавт. (Schley et al.) [20], где периваскулярное пространство моделировалось как пустое кольцевое пространство с шириной 100–150 нм). Следовательно, в данном случае нет никаких противоречий между нашей моделью и их моделью.

Как было ранее упомянуто во введении, комбинированные эффекты перистальтического движения стенки кровеносного сосуда и влияние лечения по методу конвекционно-усиленной доставки лекарств представляют наибольший интерес. При лечении данным методом лекарства впрыскиваются непосредственно в мозговую ткань (серое вещество) через иглу или катетер. Макроскопическое давление, приложенное к точке от источника впрыскивания [15], имеет следующий вид:

p ( r ) = P-a , (16)

R где P0 – давление в полости, заполненной жидкостью с радиусом a, окружающим источник, а R – расстояние от источника. Типичным значением для P0 является 7 кПа, а для a – 13 мкм [15].

В зоне R градиент микроскопического давления вдоль направления R равен dP _ P0 ■ a

dR " 1R

Взаимодействие между перистальтическим движением стенок кровеносного сосуда и внешним градиентом давления вследствие конвекционно-усиленной доставки зависит от расположения кровеносного сосуда. Например, если кровеносный сосуд в области R расположен перпендикулярно к направлению R , то градиент внешнего давления будет оказывать незначительное влияние на градиент давления в периваскулярном пространстве вдоль направления кровеносного сосуда. Для авторов интересен случай, при котором кровеносный сосуд ориентирован вдоль направления R при рассмотрении этой области, перистальтическая волна распространяется кнаружи. В этом случае изменение давления на длине волны A p _л в уравнении (13) может быть

P ■ a .

вычислено как — ■ л , тогда

R ²

Q ( 1 ) _ ns cR ₂ ² <

R 1

г

R 2 )

2( κ P ₀ a ε c µ R ²

b

+

^- 1)

+ 1

г

-

R 1

V ¹ 2 )

^ ( ^b 1 ² V ¹ 2 )

^ . (18)

V R 2 )

¹ + it

V R 2 )

г

b

V ¹ 2 )

Отметим, что Q зависит от рассмотрения расположения зоны R относительно кровеносного сосуда. Для сравнения эффектов терапии при конвекционно-усиленной доставке лекарств в присутствии и отсутствии перистальтического движения стенок кровеносного сосуда введем следующее безразмерное число:

log R, мкм

a

б

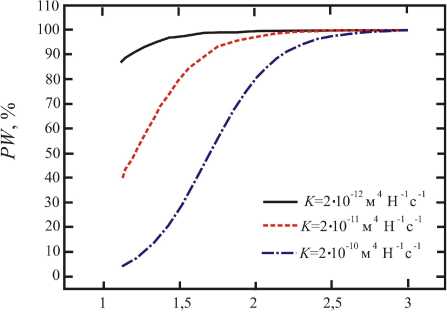
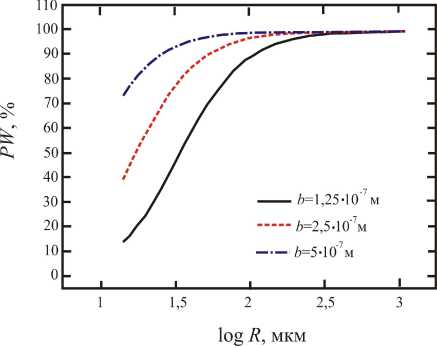
Рис. 2. Зависимости PW oт log R : a – при трех различных значениях K с асимптотой, равной b ; б – при трех различных значениях b с асимптотой, равной значению K

PW ( R ) = Q ⁽ R ^Q^b = 0 1⁰⁰%, (19)

где PW – сокращение от “ peristaltic wave ” («перистальтическая волна»). Это число характеризует вклад доставки жидкости от перистальтической волны. Можно показать, что величина PW всегда неотрицательная.

На данном этапе авторы испытывают необходимость в экспериментальных данных для непосредственного сравнения с теоретическими результатами. Следовательно, необходимо провести анализ чувствительности к параметрам, принятым в модели. Выберем b и K как варьируемые параметры и зафиксируем остальные параметры, поскольку в литературе наблюдается их разброс согласно приведенным данным. Зависимости PW от log R показаны на рис. 2, где R меняется от a до 1000 мкм. На рис. 2, a была построена зависимость PW (%) от log R (мкм) для трех различных значений K с асимптотой b, а на рис. 2, б зависимости PW (%) от log R (мкм) строились для трех различных значений b c асимптотой K. Как можно увидеть из рис. 2, транспортировка жидкости в периваскулярное пространство в большей степени обеспечивается конвекционно-усиленной добавкой, так и перистальтическая волна чувствительна к расположению R и, в частности, к значению b и K. Во всех случаях, изображенных на рис. 2, в зоне, которая находится далеко от источника впрыскивания лекарства (~1000 мкм) транспортирование жидкости главным образом осуществляется за счет перистальтической волны. Рядом с источником впрыскивания перистальтическая волна играет важную роль или не зависит от выбора значений параметров. В некоторых случаях даже рядом с источником впрыскивания перистальтическая волна может всё ещё вносить большой вклад (например, её показатель равен 80% рядом с R = a при b = 2,5· 10–7 м и K = 2· 10–12 м4/(Н·с)). Поскольку K – гидравлическая проницаемость периваскулярного пространства, её снижение должно привести к увеличению процентного вклада перистальтической волны, что согласуется с рис. 2, а. Так как b – половина амплитуды волны, то при увеличении значения b, вклад перистальтической волны должен увеличиваться, что согласуется с рис. 2, б. Отметим, что при анализе чувствительности параметры b увеличивались в 2 раза, в то время как параметры K – в 10 раз. Авторам кажется, что система уравнений больше чувствительна к изменению b, чем к изменению K. Как обсуждалось выше, при некоторых условиях система является аддитивной (см. (15)). Чувствительность PW к значениям b и K можно интерпретировать, учитывая, что скорость течения жидкости вследствие конвекционно-усиленной доставки пропорциональна К (первое слагаемое в правой части (15)), в то время как скорость течения вследствие перистальтической волны (второе слагаемое в правой части (15)) пропорциональна b2.