Механико-математическая модель интрастромальной коррекции формы роговицы глаза при кератоконусе
Автор: Никитин И.С., Журавлев А.Б., Ирошников Н.Г., Ларичев А.В., Никитин А.Д.
Журнал: Российский журнал биомеханики @journal-biomech
Статья в выпуске: 4 (78) т.21, 2017 года.
Бесплатный доступ
Предложена механико-математическая модель коррекции кератоконуса роговицы глаза, которая позволяет численно моделировать деформацию и изменение формы роговицы при внедрении гибкого кольцевого импланта в заранее подготовленный для него микроканал. Импланты представляют собой два кольцевых сегмента с радиусом большим, чем радиус подготовленных каналов. Материал имплантов - полиметилметакрилат. С помощью этой хирургической операции возможно разглаживание дефекта роговицы (кератоконуса). В механико-математической модели коррекции кератоконуса решается задача совместного контактного деформирования гибких кольцевых сегментов и роговицы глаза. Для создания геометрической 3 D -модели роговицы использовались данные измерений, сделанных до и после операции коррекции кератоконуса у пациентов клиники микрохирургии глаза. Координаты реальных поверхностей роговицы были представлены в виде полиномов Цернике. На основе этой модели разработан программный комплекс, позволяющий рассчитывать изменение формы роговицы после внедрения имплантов. Предложенный метод моделирования операции коррекции кератоконуса дает возможность проводить численную оценку и оптимизацию механических свойств и геометрических параметров кольцевого импланта для достижения желаемого эффекта - исправления дефекта роговицы глаза.
Роговица глаза, кольцевой имплант, коррекция кератоконуса, механико-математическая модель, метод конечных элементов, полиномы цернике
Короткий адрес: https://sciup.org/146281835
IDR: 146281835 | УДК: 539.3 | DOI: 10.15593/RZhBiomeh/2017.4.07
Текст научной статьи Механико-математическая модель интрастромальной коррекции формы роговицы глаза при кератоконусе
Предложена механико-математическая модель интрастромальной коррекции формы роговицы глаза при кератоконусе – заболевании, при котором роговица принимает коническую форму. Кератоконус может привести к серьёзному ухудшению зрения.
Суть операции коррекции формы роговицы состоит в следующем. В ходе операции фемтосекундным лазером в структуре роговицы выполняют два полукруглых
Журавлев Алексей Борисович, к.ф.-м.н., с.н.с. лаборатории геомеханики, Москва
Ларичев Андрей Викторович, к.ф.-м.н., с.н.с. кафедры медицинской физики, Москва
Никитин Александр Дмитриевич, к.т.н., н.с. отдела математического моделирования, Москва микроканала для последующего помещения туда имплантов. Импланты представляют собой два кольцевых сегмента с радиусом большим, чем радиус подготовленных каналов. Материал имплантов – полиметилметакрилат. Эти гибкие кольцевые сегменты, вставленные в микроканалы, стремятся восстановить свою начальную форму, тем самым деформируя и растягивая роговицу. При этом разглаживается дефект ее формы – кератоконус.
Ранее в [1,2] рассматривалась модель этой операции с упрощенным описанием деформирования импланта обыкновенным дифференциальным уравнением изгиба Бернулли-Эйлера. Кроме того, не проводилось исследование и сравнение результатов расчета для актуальных форм роговицы до и после операций, проведенных с конкретными пациентами клиники микрохирургии глаза.
В предложенной механико-математической модели коррекции кератоконуса решается задача совместного контактного деформирования гибких кольцевых сегментов и роговицы глаза. Деформирование кольцевых сегментов описывается системой дифференциальных уравнений изгиба криволинейного кольцевого стержня [3]. Деформирование роговицы глаза с дефектом рассчитывается методом конечных элементов как трехмерная задача для квазисферического сегмента [4]. Для создания 3D-модели использовались данные измерений, сделанных до и после операции коррекции кератоконуса у пациентов клиники микрохирургии глаза. Координаты реальных поверхностей роговицы были представлены в виде полиномов Цернике [5].
На основе этой модели разработан программный комплекс, позволяющий рассчитывать изменение формы роговицы после внедрения имплантов. Основные расчеты проводились для треугольного сечения кольцевого сегмента, используемого в медицинской практике.
Поскольку поверхность модели строилась по точкам, полученным в результате измерений реальной роговицы, ее форма изначально включает деформации, вызванные воздействием внутриглазного давления. По этой причине внутриглазное давление в расчетах не прикладывается, исследеются изменение формы роговицы в результате операции.
Предложенная механико-математическая модель позволит оптимизировать геометрические и механические характеристики кольцевого сегмента, вставляемого в роговицу для коррекции дефекта.
Данные измерений
3D-модель роговицы глаза построена на основе данных измерений, сделанных офтальмологами Клиники глазных болезней (г. Москва) под руководством проф. М.Д. Пожарицкого. Были измерены координаты внешней и внутренней поверхностей роговицы для ряда пациентов клиники микрохирургии глаза до и после проведения операции коррекции кератоконуса. Данные получены с использованием современной медицинской аппаратуры Pentacam и представлены в виде коэффициентов (амплитуд) полиномов Цернике [5]. Такого рода представления в настоящее время широко используются при исследовании кривизны поверхностей и аберрации волнового фронта для решения задач дифференцированной диагностики оптических структур глаза.
Координаты поверхности роговицы задаются с помощью полиномов Цернике:
Z (p, 6)=E Ak • zk (p, 6),
k определенных в цилиндрической системе координат (рис. 1): ρ = r/R0, R0 – радиус области измерений, реальное значение R0 = 4 мм, Ak – измеряемые амплитуды полиномов. Используются первые 28 членов.
Для краткости в таблице представлены вид 10 полиномов и данные измерений внешней и внутренней поверхностей роговицы пациента А.К., полученных на Pentacam е.
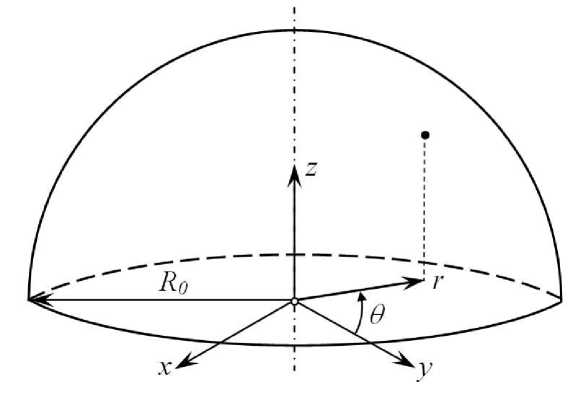
Рис. 1. Координаты точки поверхности роговицы
Данные измерений
|
k |
Полиномы Цернике zk |
Амплитуды полиномов Ak , мм |
|||
|
внешняя поверхность |
внутренняя поверхность |
||||
|
до операции |
после операции |
до операции |
после операции |
||
|
1 |
1 |
0,000000 |
0,000000 |
0,000000 |
0,000000 |
|
2 |
2 p cos 0 |
0,000000 |
0,000000 |
0,000000 |
0,000000 |
|
3 |
2 p sin 0 |
0,000000 |
0,000000 |
0,000000 |
0,000000 |
|
4 |
V3 ( 2 p 2 - 1 ) |
0,243014 |
0,227426 |
0,298931 |
0,276392 |
|
5 |
V6p 2 sin 2 0 |
0,004978 |
–0,001043 |
0,011428 |
-0,033586 |
|
6 |
V6p 2 cos 2 0 |
0,015242 |
0,014065 |
0,021741 |
0,053614 |
|
7 |
V8 ( 3 p 3 - 2 p ) sin 0 |
–0,003267 |
0,000218 |
–0,006042 |
–0,016666 |
|
8 |
V8 ( 3 p 3 - 2 p ) cos 0 |
0,007641 |
0,007726 |
0,009798 |
0,025392 |
|
9 |
V8 p 3 sin 3 0 |
0,000207 |
0,001766 |
0,001244 |
0,005499 |
|
10 |
V8 p 3 cos 3 0 |
–0,000363 |
0,000389 |
–0,003581 |
–0,007405 |
По данным таблицы могут быть найдены координаты точек поверхности.
Геометрическая модель роговицы
Согласно данным измерений профили поверхности реальной роговицы отличаются друг от друга при разных азимутальных углах θ , т.е. роговица, строго говоря, не является телом вращения.
Метод построения 3D-моделей таких тел заключается в создании максимального количества опорных профилей, т.е. контуров объекта в сечениях θ = const. Ограничивающие поверхности тела образуются «натягиванием» на опорные профили как на каркас. Поскольку такой метод весьма трудоемок, возникает вопрос о разумной достаточности количества опорных профилей.
Сравнение профилей роговицы при различных азимутальных углах и анализ зависимости от угла деформирующего воздействия импланта позволяют сделать вывод о допустимости ограничиться рассмотрением на данном этапе одной четвертой части полной развертки. Будет рассматриваться первый квадрант.
Для дальнейшего сопоставления данных измерений и расчета необходимо изначально установить соответствие начала отсчета углов при измерениях и положения импланта в расчете. Будем считать, что сечению, проходящему через центр импланта, соответствует опорный профиль, в котором уплощение роговицы минимально. Данное предположение основано на том факте, что в центре импланта минимально распирающее воздействие.
На основе полученных для внешней и внутренней поверхности до операции контуров были построены опорные профили. За пределами области измерений ( ρ ≥ 1) контуры пролонгируются касательными окружностями до общей высоты реального профиля 2,4 мм. Получившееся основание, для которого нет данных измерений, необходимо в дальнейшем для проведения микроканала под имплант и постановки условий крепления роговицы к склере.
Эскизы профилей располагаются в 10 вертикальных плоскостях, определяемых азимутальными углами θ k , далее создается 3D-модель по сечениям (рис. 2).
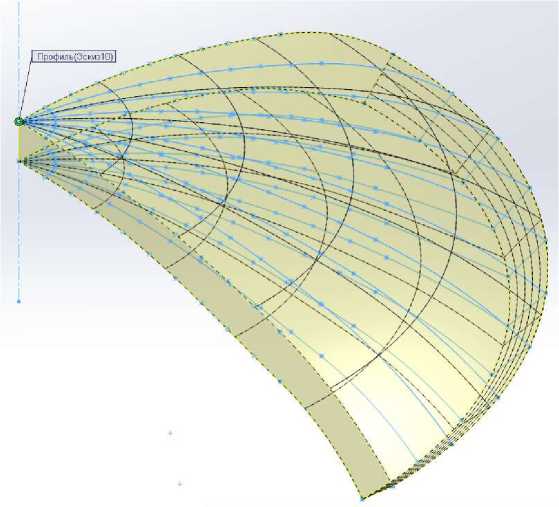
Рис. 2. 3D-модель роговицы
Механико-МАТЕМАТИЧЕСКАЯ модель деформирования роговицы
И ГИБКОГО КОЛЬЦЕВОГО СЕГМЕНТА
Система дифференциальных уравнений для изгиба плоского кольцевого тонкого упругого стержня имеет вид [3]
д N д Q Q д M
—+Q = 0,^ - N - qR = о —+QR = о, дф дф дф
„ EJ ди
M =---
R дф
и = - [ V
RI
д W ) д V+-- , W = —.
дф) дф
где N , Q – нормальная и перерезывающая силы соответственно; M – изгибающий момент в текущем сечении стержня в его плоскости; V , W – смещения стержня в тангенциальном и радиальном направлениях соответственно; q – внешние распределенные (погонные) нагрузки в плоском стержне, направленные по радиусу; E – модуль Юнга материала импланта; J – момент инерции его сечения; φ – угол, задающий координату срединной линии стержня с кольцевым радиусом R , сечению φ = 0 в силу симметрии соответствует середина кольцевого импланта, 0< φ < φmax .
Граничные условия для этой системы дифференциальных уравнений задают отсутствие воздействий при φ = φmax = γ :
Q = N = M = 0. (2)
Из системы уравнений (1) можно получить уравнение для смещения стержня в тангенциальном направлении:
д 6 V _д 4 V д 2 V R 4 / х
—7+2 —т +—7 = —q ( ф ) • дф 6 дф 4 дф 2 EJ v ’
Решение уравнения (3) для V состоит из общего решения однородного уравнения, частного решения неоднородного и имеет вид:
V(ф) = A0 + A1 sin ф + A2 cos ф + А3ф + A4фsinф + A5фcos ф + V0 (ф), где V, (ф) - частное решение неоднородного уравнения для V(ф).
Составляющие решения A 0 + A 1 sin ф + A 2 cos ф характеризуют смещения стержня как жесткого целого и при их отсутствии должны приравниваться нулю.
Неизвестную контактную нагрузку на кольцевой имплант со стороны роговицы в силу симметрии задачи по угловой координате φ будем искать в виде разложения по четным степеням φ :
q ( ф ) = q 0 + q 2ф2 /2! + q 4ф4 /4! + ....
Дифференциальное уравнение (3) с учетом граничных условий (2) можно решить аналитически. Выражения для радиальных смещений W k ( k = 0, 2, 4), соответствующих приложенными нагрузками вида q = 1, ф 2 /2! и ф4/4! (далее -«парциальные смещения» импланта), имеют вид
Wo =
R 4 2 EJ
(2 + sin у (sin ф + ф cos ф) + cos у (cos ф - ф sin ф)),
W =
R 4
2 EJ
W 4 =
ф2 - 4 + ( ( Y 2 / 2 — 1 ) sin Y + YcosY ) ( sinФ + ФcosФ )
+ ( ( Y 2 /2 - 1 ) cos y - YsinY ) ( cosФ - ФsinФ )
r 4 ф4 /12 - 2ф2 + 6 + ( ( y 4 /24 - Y 2 / 2 + 1 ) sin Y + ( Y 3 / 6 - Y ) cos Y ) ( sin ф + ф cos ф )
2 EJ
+( (y4 /24 - Y2 / 2 + 1)cos Y V
Y 3 / 6 - Y ) sin Y ) ( cos ф - ф sin ф )
Ограничиваясь тремя членами разложения, в силу линейности задачи деформирования кольцевого импланта его радиальное смещение можно представить в виде
W ( ф ) = qoWo ( ф )+q 2W2 ( ф )+q 4W4 ( ф ) •
Нагрузку на стенку микроканала в роговице, т.е. контактное давление предварительно напряженного импланта, также ищем в виде разложения по четным степеням φ, ограничиваясь тремя членами p (ф) = (qo + q 2ф2 / 2! + q 4ф4 / 4!) / h, где h – ширина стенки микроканала, испытывающей воздействие импланта.
Тогда, в силу линейности упругой задачи, радиальные смещения стенки канала представляют собой линейную комбинацию
U (ф) = qoUo (ф)+q 2U 2 (ф)+q 4U4 (ф) , где Uo, U2 и U4 - смещения, вызванные приложенными нагрузками вида q = 1, ф2 /2! и φ4 /4! соответственно (далее – «парциальные смещения» роговицы).
Угол ф определяет положение точки на стенке канала, отсчитывается от плоскости 0 = o ° , максимальный угол раствора импланта в медицинской практике имеет значение у = фт„ = 8o ° . max
γ
φ
Начальное состояние импланта
Микроканал в роговице
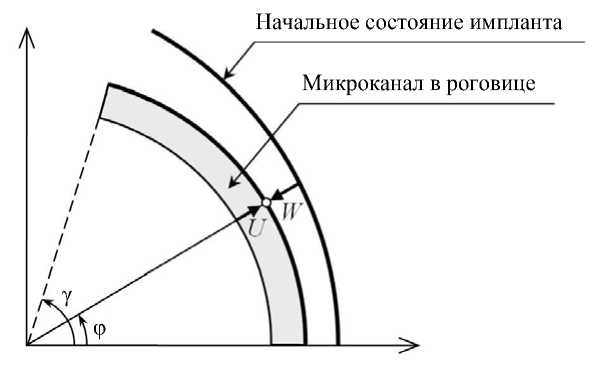
Рис.3. Геометрия смещений роговицы и импланта
Для определения контактных нагрузок следует использовать геометрическое условие совместности смещений импланта и роговицы (рис. 3):
U (ф) + W (ф) = Д W (ф).
Здесь Д W (ф) - радиальное расстояние между точками микроканала и кольцевого импланта в исходном недеформированном состоянии.
Из элементарного геометрического анализа в линейном приближении следует, что
Д W = R^ + r 1 2 - 2 R1 r cos ( ф - ф ) /2,
R1 = 2R sin(y /2), r1 = 2r()sin(ф /2), ф = г0ф / R, где r0 – радиус кривизны микроканала в сечении роговицы; R – радиус кривизны импланта (кольцевого сегмента) до операции.
Следовательно, с учетом принятой формы разложения по углу φ три неизвестные амплитуды qj , j = 0, 2, 4 могут быть определены из условия совместности смещений в трех точках контура канала, например, ф k = 0, у / 2, у (см. рис. 3):
qj(Ujk + Wjk) = Д w (ф k), где Wjk - определенные выше парциальные перемещения импланта в точках фk, Wjk = Wj (фk); Ujk - парциальные смещения стенки роговицы в точках фk, Ujk = Uj(фk).
Таким образом, расчет должен начинаться с решения трех вспомогательных задач линейной теории упругости с помощью метода конечных элементов для роговицы с микроканалом со стандартной формой нагрузок: q j = 1, ф2 /2! и ф 4 /4!. Расчет проводился с помощью прикладного метода конечных элементов пакета Astra [4]. Из этих численных решений были найдены ее парциальные смещения, определяющие, в свою очередь, амплитуды комбинированной нагрузки. Типичный пример расчета распределения нагрузки по стенке канала показан на рис. 4.
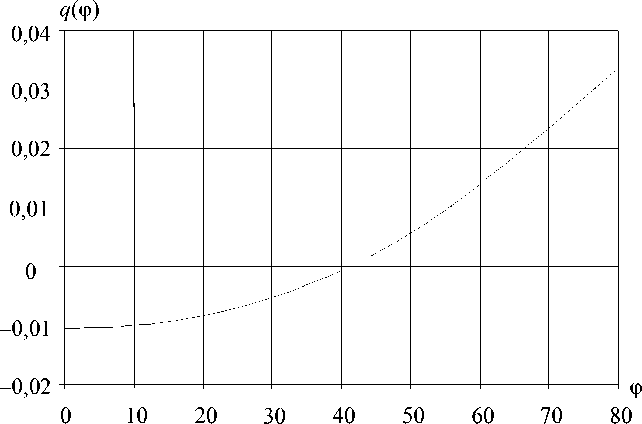
Рис. 4. Распределенная нагрузка от положения на стенке канала
Амплитуда нагрузки, разумеется, зависит от свойств материала и положения выреза, однако ее форма принципиально остается неизменной. Имеют место распор стенки канала на концах импланта и малое сжатие в центре.
Подготовка модели к расчету
Целью расчетов является исследование изменения формы роговицы в результате растягивающего воздействия кольцевого импланта и сопоставление полученных результатов с данными измерений формы поверхности роговицы до и после операции у реальных пациентов. С этой целью модель, способ построения которой описан выше, нагружается растягивающим давлением, соответствующим воздействию импланта. Имплант как часть конечно-элементной модели не рассматривается. Для моделирования его воздействия проводится полукольцевой микроканал, имеющий в поперечном сечении треугольную форму реального импланта, к боковой поверхности канала прикладывается распределенное давление.
Поскольку остается открытым вопрос о механических свойствах реальной роговицы, степени ее неоднородности, анизотропии свойств, возможности нелинейного деформирования, а также условиях закрепления на склере, расчетная модель должна давать возможность вариации перечисленных параметров. Не полностью определена также ориентация в пространстве операционного канала: расстояние от области измерений, степень горизонтальности его образующей.
Для обеспечения возможности варьировать прочностные свойства модели роговицы в разных ее частях, а также для более корректного задания распределенной нагрузки, имитирующей воздействие импланта, модель делится на четыре части: горизонтально – по плоскости измерений, вертикально – по сечению, соответствующему середине импланта, в данном случае азимутальный угол сечения составляет 40 ° .
Далее строится полукольцевой микроканал для приложения нагрузки. Его сечение совпадает с сечением кольцевого импланта и имеет форму треугольника. Вертикальное положение микроканала на практике определяется приблизительно на трети высоты роговицы. Микроканал проводится от фронтальной плоскости вращением вокруг вертикальной оси на 80 ° согласно форме импланта.
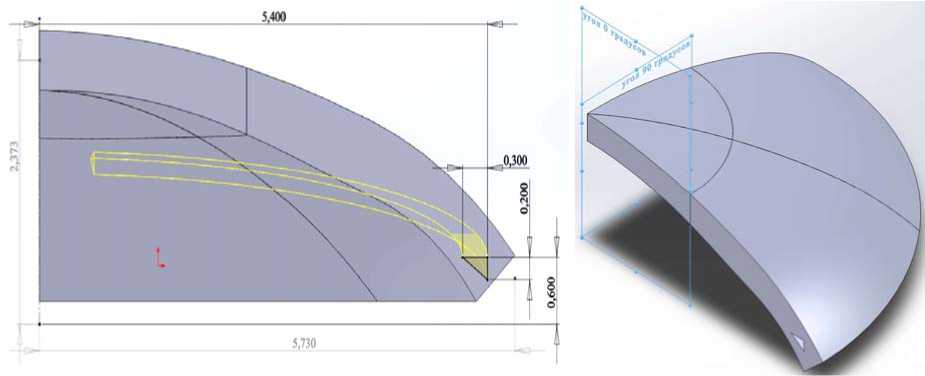
а б
Рис. 5. Модели: а – микроканал с наклоном;
б – 3D-модель роговицы с микроканалом
Было исследовано несколько вариантов высоты проведения канала. В результате тестовых расчетов было обнаружено, что имплант тем больше влияет на изменение формы роговицы (в области измерений), чем выше расположен микроканал. Исходя из сопоставления расчетов с данными измерений при различных азимутальных углах был сделан вывод, что реальный микроканал проведен наклонно. В окончательном варианте модели микроканал проведен в плоскости, повернутой относительно фронтальной на 10 ° (рис. 5).
Таким образом, микроканал находится далеко от области измерений в плоскости с азимутальным углом 9 = 0 ° и достаточно близко при 9 = 90 ° . В окончательной форме 3 D -модель представлена на рис. 5, б .
Обсуждение результатов расчета
Основной формой представления результатов будут графики профилей деформированной роговицы в сопоставлении с данными измерений. Графики построены в сечениях плоскостями 9 = 0 ° и 9 = 90 ° (рис. 6).
Данные по модулям упругости биоматериала роговицы были взяты из [6, 7]. О существенно анизотропных (ортотропных) упругих свойствах материала роговицы говорилось в [8].
Основные расчеты проводились для треугольного сечения кольцевого сегмента, используемого в медицинской практике. Стороны треугольника имели размеры h = 0,3 мм, d = 0,2 мм. Модуль Юнга импланта (полиметилметакрилат) равен Е имп = 2800 МПа. Для модуля Юнга роговицы существует большая неопределенность, отмеченная в [6]. В различных источниках приведены значения в широком диапазоне от Е рог = 1,2 МПа [7] до Е рог = 0,54 МПА [6, ссылка на Woo , 1972], и даже до Е рог = 0,34 МПа [6, ссылка на Hoeltzel, 1992]. Это можно объяснить как упругой анизотропией материала роговицы, так и неоднородностью его свойств по месту измерения, на которое обычно нет указаний. Естественно, играют роль и индивидуальные особенности пациента.
Приведем результаты расчета параметров послеоперационной роговицы при строго горизонтальном проведении микроканала. Рассматривался ортотропный материал с продольной жесткостью E rr = 1,0 МПа и поперечной E zz = 0,3 МПа, v = 0,49.
Сопоставляются различные вертикальные положения микроканала (см. рис. 6, а , б ).
Хорошо видно, что высоко проведенный микроканал в большей степени влияет на периферийную часть зоны измерений. Здесь распор слишком велик по сравнению
z ( r )
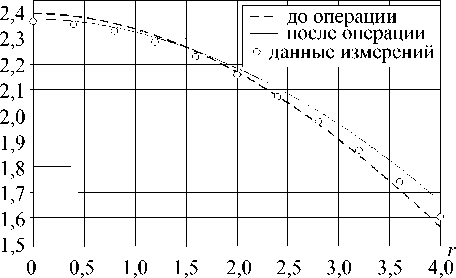
а
z ( r )
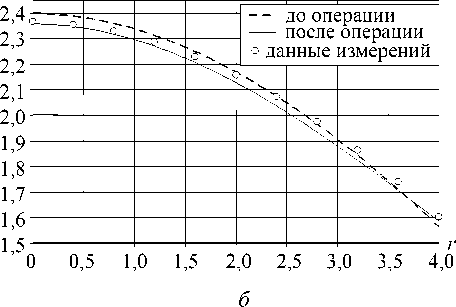
Рис. 6. Профили роговицы в сечении 9 = 90 ° : а – микроканал выше; б – микроканал ниже
с данными измерений. В то же время в центральной части просадка контура заметно ниже реальной.
При низко проведенном микроканале картина обратная: данные измерений в центре хорошо ложатся на расчетную кривую, однако периферия растянута недостаточно. Аналогичная картина наблюдается и в других сечениях.
Была исследована зависимость распределения перемещений роговицы при различных условиях закрепления внешнего контура: а) при полностью фиксированном внешнем контуре, б) при ограничении только на вертикальные перемещения опорной кромки, при этом допускается свободное проскальзывание в горизонтальной плоскости. Хотя картина смещений существенно меняется, однако оба варианта расчета значительно отличаются от данных измерений.
Перейдем к рассмотрению базовой конфигурации с наклонным каналом.
Наилучшее соответствие результатов измерений и расчета было достигнуто при учете не только анизотропных, но и неоднородных упругих свойствах роговицы. Фронтальная (полюсная) часть роговицы имеет пониженные упругие модули, что объясняет само развитие дефекта кератоконуса у пожилых людей ослаблением тканей в этой части роговицы
Рассматривался ортотропный неоднородный материал с продольной жесткостью верхней части Err = 0,5 МПа и поперечной Ezz = 0,4 МПа для основания: продольная жесткость Err = 1,3 МПа, поперечная Ezz = 0,6 МПа, ν = 0,49. С учетом исследования влияния условий закрепления выбрано условие закрепления посредством упругого основания с переменной жесткостью. При этом допускаются перемещения внешнего контура во всех направлениях и обеспечиваются условия равновесия.
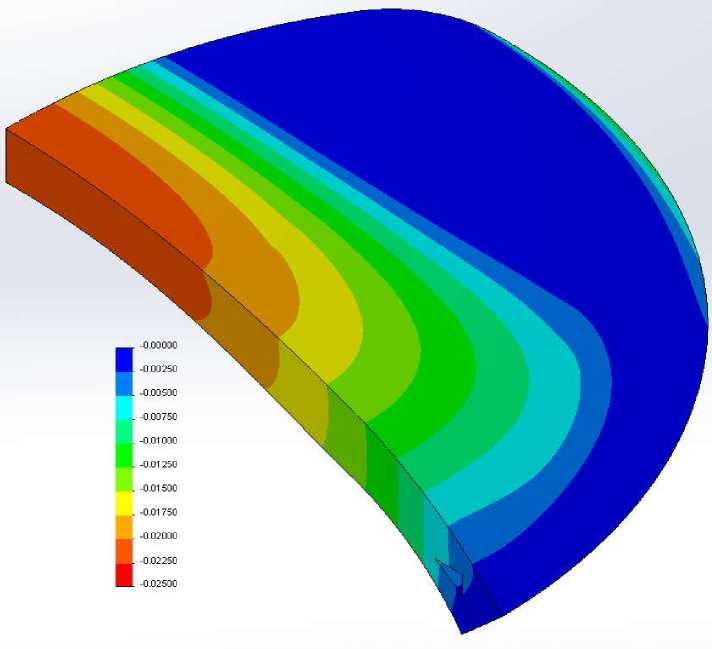
На рис. 7 представлены линии уровня перемещений.
В рассмотренной конфигурации максимум просадки располагается в центре роговицы, что соответствует данным измерений, значение его близко к фактическому. На внешнем контуре заметны отличные от нуля вертикальные перемещения. Этот результат, полученный благодаря применению условия упругого основания, соответствует реальности, поскольку роговица закреплена не жестко, а на податливой склере.
На рис. 8 представлены графики деформированного контура роговицы в сопоставлении с данными измерений.
Точки данных измерений удовлетворительно ложатся на расчетную кривую. Наилучшее совпадение получено на границе области измерений. Сближение значений просадки в центральной части роговицы может быть достигнуто вариациями продольной/поперечной жесткости.
Расхождение может быть обусловлено тем, что отсутствуют данные о габаритах роговицы, форме основания и радиальных смещениях точек контура в результате операции.
Результаты численных экспериментов показывают, что небольшие вариации модулей при соблюдении общего масштаба отличий в неоднородности слабо влияют на картину смещений роговицы. Точки измерений значительно лучше ложатся на сплошную расчетную кривую формы роговицы после операции на рис. 8 (неоднородный ортотропный случай), чем на рис. 6 (однородный ортотропный случай).
Также было исследовано возможное влияние нелинейно упругого деформирования на изменение контура роговицы. Рассматривается та же геометрическая модель при тех же нагрузках. Модуль упругости верхней части: E 1 = 0,5 МПа, модуль упругости основания: E 2 = 1,3 МПа, ν = 0,49.
Предполагалось, что при достижении порогового значения деформаций ε 0 материал начинает деформироваться нелинейно упруго, при этом модуль упрочнения остается постоянным и составляет 0,10 значения модуля упругости (билинейная диаграмма деформирования).
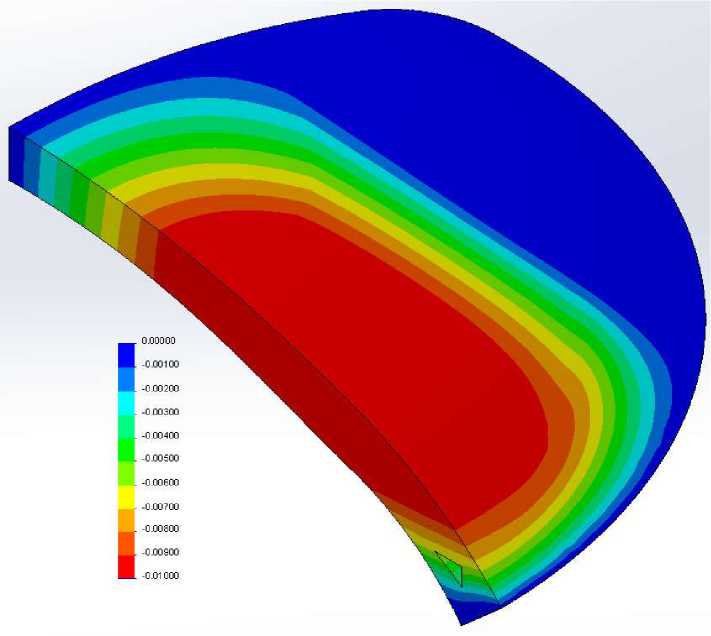
а
б
Рис. 7. Перемещения роговицы: а – горизонтальные; б – вертикальные
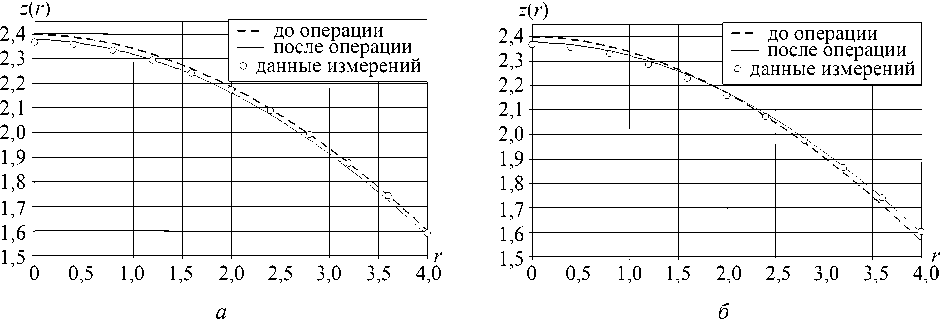
Рис. 8. Контур роговицы : а - сечение 9 = 0 ° ; б - сечение 9 = 90 °
С учетом достигаемого в упругом расчете уровня деформаций, были рассмотрены два варианта пороговых значений: s 0 = 0,005 и 0,0025.
В первом случае ε0 = 0,005 область нелинейного деформирования занимает малую окрестность участков максимального контактного давления, сжатия в центре импланта и растяжения на краю. В центральной части роговицы условия перехода к нелинейному деформированию не выполняются, поэтому распределение перемещений мало отличается от линейно упругого.
На рис. 9 представлены графики деформированного контура роговицы в сопоставлении с данными измерений, s 0 = 0,005.
В целом графики похожи на упругое решение (см. рис. 8). Просадка в центре несколько больше вследствие наличия области нелинейно упругого деформирования, заметное расхождение в основании связано с тем, что в нелинейной постановке невозможен расчет с использованием условия упругого основания.
Во втором случае при низком пороге s 0 = 0,0025 нелинейно упругим деформированием охвачена значительная часть объема. Полностью в области нелинейности верхняя часть роговицы. Это заметно сказывается на величине вертикальной постоперационной просадки, ее значения в центре значительно выше фактических. На рис. 10 представлены графики деформированного контура роговицы в сопоставлении с данными измерений, s 0 = 0,0025.
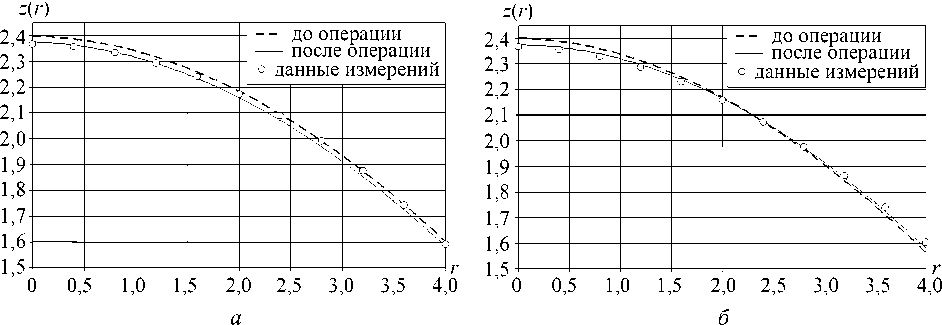
Рис. 9. Контур роговицы в сопоставлении с данными измерений, е 0 = 0,005: а - сечение 9 = 0 ° ; б - сечение 9 = 90 °
z ( r )
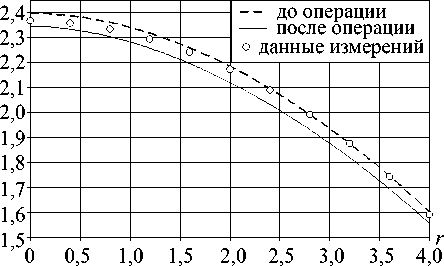
а
Рис. 10. Контур роговицы в сопоставлении с данными измерений, е 0 = 0,0025: а - сечение 0 = 0 ° ; б - сечение 0 = 90 °
z ( r )
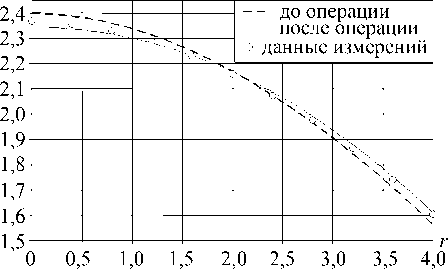
б
Точки данных измерений почти везде значительно отстоят от расчетной кривой. Совпадение на краю области измерений объясняется отсутствием условия упругого основания и использованием условия фиксации внешнего контура.
В целом модель с учетом нелинейного деформирования роговицы описывает реальную ситуацию хуже, чем линейная ортотропная.
Наилучшее совпадение результатов измерений и расчетов по предложенной модели получено для неоднородного ортотропного материала роговицы с условием упругого крепления к основанию.
Заключение
Предложенная механико-математическая модель позволяет численно моделировать деформацию и изменение формы роговицы глаза при внедрении гибкого кольцевого сегмента в заранее подготовленный для него канал. С помощью этой хирургической операции возможно исправление дефекта роговицы (кератоконуса).
В механико-математической модели коррекции кератоконуса решается задача совместного контактного деформирования гибких кольцевых сегментов и роговицы глаза. Деформирование кольцевых сегментов описывается системой дифференциальных уравнений изгиба криволинейного кольцевого стержня. Деформирование роговицы глаза с дефектом рассчитывается методом конечных элементов как трехмерная задача для квазисферического сегмента. Для создания геометрической 3 D -модели роговицы использовались данные измерений, сделанных до и после операции коррекции кератоконуса у пациентов клиники микрохирургии глаза. Координаты реальных поверхностей роговицы представлены в виде полиномов Цернике. На основе этой модели разработан программный комплекс, позволяющий рассчитывать изменение формы роговицы после внедрения имплантов.
Показано, что наилучшее совпадение результатов измерений и расчетов по предложенной модели получено для неоднородного ортотропного материала роговицы с условием упругого крепления к основанию (склере). Модель с учетом нелинейного деформирования роговицы описывает реальную ситуацию хуже, чем линейная ортотропная.
Предложенный метод моделирования операции коррекции кератоконуса позволяет проводить численную оценку и оптимизацию механических свойств и геометрических параметров кольцевого импланта для достижения желаемого эффекта – разглаживания дефекта роговицы глаза.
Благодарности
Работа выполнена в рамках проекта РФФИ № 15-29-03895офи_м.
Список литературы Механико-математическая модель интрастромальной коррекции формы роговицы глаза при кератоконусе
- Биргер И.А. Круглые пластинки и оболочки вращения. - М.: Оборонгиз, 1961. - 368 с.
- Бураго Н.Г., Кукуджанов В.Н. Численное решение упругопластических задач методом конечных элементов. Пакет программ АСТРА // Вычислительная механика твердого деформируемого тела. - М.: Наука, 1991. - Вып. 2. - С. 78-122.
- Никитин И.С., Журавлев А.Б., Ирошников Н.Г., Якушев В.Л. Математическая модель интрастромальной коррекции формы роговицы глаза // Современные проблемы механики сплошной среды: тр. XVIII Междунар. конф. (Ростов-на-Дону, 7-10 ноября 2016г.): в 2 т. - Ростов-н/Д: Изд-во Южню федер. ун-та, 2016. - Т. 2. - С. 141-145.
- Смотрич Е.А. Топография роговицы и распределение механических напряжений в ней при различных видах корнеальной хирургии: дис. … канд. мед. наук: 14.01.07. Глазные болезни. - М., 2014. - 85 с.
- Хусаинов Р.Р., Цибульский В.Р., Якушев В.Л. Моделирование деформации глаза при измерении внутриглазного давления оптическим методом // Журнал вычислительной математики и математической физики. - 2011. - Т. 51, № 2. - С. 349-362.
- Oliveira C.M., Ferreira A., Franco S. Wavefront analysis and Zernike polynomial decomposition for evaluation of corneal optical quality // J. Cataract. Refract. Surg. - 2012. - Vol. 38, № 2. - P. 343-356.
- Larichev A., Nikitin I., Yakushev V. Computer simulation of intrastromal correction shape of the cornea in keratoconus // Proceedings of 8th European Meeting on Visual and Physiological Optics. - Antwerp, 2016. - P. 50-52.
- Pandolfi A., Manganiello F. A model for the human cornea: Constitutive formulation and numerical analysis // Biomechanics and Modeling in Mechanobiology. - 2006. - № 5. - P. 237-246.


