Механизмы в структуре виброзащитных систем: математические модели, оценка динамических свойств (часть I)

Повышение требований к динамическому качеству машин, точности исполнения рабочих движений, обеспечению надежности работы деталей, узлов и сопряжений при знакопеременных нагрузках приводит к необходимости оценки, контроля и управления динамическим состоянием технической системы в целом и ее отдельных узлов. Надежность и безопасность функционирования машин закладывается в предпроектных исследованиях и обеспечивается на всех стадиях проектирования, производства и эксплуатации. Создание современных машин опирается на соответствующую научную основу, создаваемую в области машиноведения, теоретической механики, теории механизмов, динамики и прочности машин [1, 2].

Решение задач вибрационной защиты все чаще рассматривается как разработка способов и средств управления динамическим состоянием технических объектов, в структуру которых входят многочисленные узлы и механизмы, взаимодействующие между собой в условиях интенсивных внутренних и внешних периодических и ударных возмущений [3].

Для теоретических основ современного машиностроения и робототехники в частности характерна широкая интеграция теоретической механики, теории механизмов и машин, теории колебаний с методами теории автоматического управления и теории цепей. Структурные методы исследования механических колебательных систем, получившие развитие в последние десятилетия, создают возможность с единых позиций рассматривать динамические взаимодействия механизмов и устройств различной физической природы. Механические цепи в различных формах проявления, в том числе как механизмы, состоящие из взаимодействующих между собой звеньев в виде твердых тел и элементов, обладающих упругими и диссипативными свойствами, а также возможностями преобразования движения, позволяют создавать расчетные схемы, адекватные сложности современных машин. Вместе с тем механизмы обладают специфическими свойствами, что требует разработки специальных методов построения математических моделей и оценки динамических свойств виброзащитных систем [4].

В этом плане возникает ряд проблем, решение которых связано с необходимостью учета особенностей построения виброзащитных систем и конструктивно-технических форм реализации объектов защиты от внешних воздействий. Насыщение современных машин исполнительными механизмами различной физической природы, требования к регламентации параметров динамического состояния предопределяют актуальность научных исследований, направленных на поиск и разработку способов и средств обеспечения динамического качества технических объектов.

В предлагаемой статье развиваются методологические основы метода построения математических моделей виброзащитных систем, позволяющего решать задачи оценки возможностей динамических взаимодействий в механических колебательных системах дополнительных связей в виде механизмов.

Основой для решения задач динамики являются структурные методы, в рамках которых используются возможности аналитического аппарата теории автоматического управления, что обеспечивает в задачах динамического синтеза виброзащитных систем условия учета особенностей элементарных звеньев различной физической природы и особенностей их соединений и взаимодействия. Предложена и разработана методологическая основа методов построения математических моделей различных механических колебательных систем, отражающих специфику работы механических систем с учетом геометрических особенностей расположения элементов и многообразных форм их взаимодействия.

Применяемые средства защиты от вибраций в структуре виброзащитных систем становятся все более разнообразными, что отражает тенденции введения и использования в вибро-защитных системах широкого набора технических средств, имеющих упруго-диссипативные и массоинерционные свойства, в том числе возможности преобразования движений.

Общие положения. Постановка задачи исследования

Используемые механизмы могут иметь разнообразную физическую природу, что предопределяет интерес к обобщению задач вибрационной защиты и разработке методов оценки динамических взаимодействий элементов и учету особенностей систем с рычажными связями и рычажными механизмами.

Большим разнообразием отличаются расчетные схемы технологических машин и транспортных средств, если иметь в виду широкое использование в механических колебательных системах механизмов и устройств для преобразования движения.

Сравнительный анализ виброзащитных систем различного назначения позволяет выделить особую значимость рычажных связей и соответствующих механизмов в создании структуры систем и формирования их упруго-диссипативных и массоинерционных свойств. По существу, типовые элементы виброзащитных систем в виде пружин, демпферов и устройств для преобразования движения являются механизмами того или иного вида, которые реализуют соответствующие динамические свойства. Конструктивные формы реализации взаимодействий предполагают необходимость определения динамических усилий в контактах и разработку методической базы силовых расчетов для обеспечения надежности работы систем и безопасности их эксплуатации.

Задача исследования заключается в разработке детализированной технологии построения математических моделей, которые адекватны формам внешних воздействий и основаны на использовании аналитического аппарата теории автоматического управления.

Развитие подходов на основе структурных интерпретаций механических колебательных систем

Рассмотрим обобщенную постановку задач вибрационной защиты с использованием базовых моделей в виде систем, совершающих малые прямолинейные поступательные и угловые колебания. На рисунке 1 а показана расчетная схема виброзащитной системы (ВЗС) с расширенным набором типовых элементов, в частности с устройством для преобразования дви- жения.

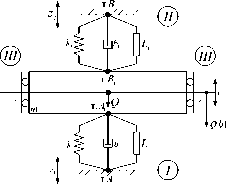
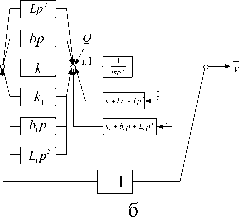
Рис. 1. Базовая расчетная схема с одной степенью свободы (а) и ее структурная схема (б); I и II – опорные поверхности

В рамках структурной теории виброзащитных систем [1] передаточные функции системы при различных наборах входных и выходных параметров имеют вид:

W ( p ) = 2 =_________ Lp ² + bp + k _________;

Q=0    z   (m + L + L)p2 +(b + b)p + kx + k’ z i =0

W ( p ) = 2 =_______ L i p ^{2 +} b p ^{+ k} i ;

Q=o    z i   (m + L + L) p2 +(b + b)p + k + k’ z=0

Wз( p ) = zi =0

z = 0

y

Q

(m + L + Lx)p2 + (b + b)p + kx + k’ где Q – силовое, а z ‒ кинематическое гармонические возмущения в изображениях по Лапласу; p = jω – комплексная переменная; k, k1 – жесткости пружин; b, b1 ‒ коэффициенты вязкого трения; L, L1 – приведенные массы устройств для преобразования движения; m – масса объекта защиты.

Выражения (1) могут быть получены из структурных схем на рисунке 1 б.

В [5] приводятся обоснования адекватности математических моделей структурного вида и дифференциальных уравнений, получаемых методом Лагранжа: разработаны правила преобразования структурных схем. Расчетная схема виброзащитной системы, совершающей угловые колебания, приведена на рисунке 2, на котором показаны возможности пространственного размещения отдельных типовых элементов системы.

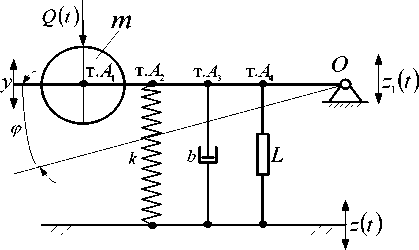
Рис. 2. Расчетная схема системы с раздельными точками крепления элементарных звеньев

Передаточная функция системы содержит информацию о параметрах точек закрепления элементов и имеет вид:

W'(p )=y

Q = 0 z z i = 0

Li 3 p + bi 2 p + ki i

( m + Li 3 ) p^ + bi 2 p + ki y

где ⁱ 3 = l j ; i 2 = у ; ⁱ 1 = l i

‒ передаточные отношения рычажных связей.

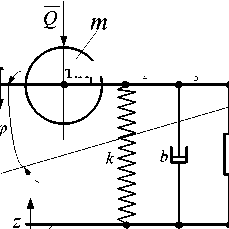
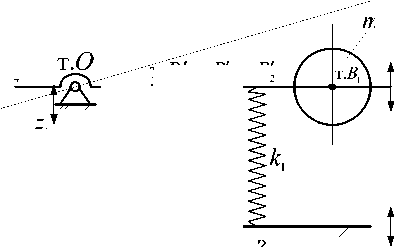
В [6] рассмотрены особенности расчета схем и виброзащиты (рис. 3) при угловых колебаниях с точкой опоры, обеспечивающей внешние воздействия разных типов (имеются в виду силовые и кинематические внешние возмущения).

y

т. A т. A т. A

‘ т.AX тA2' т. A3' T-A4

У '

z ₂

Рис. 3. Расчетная схема виброзащитной системы с разделением точек закрепления типовых элементов на невесомом стержне с промежуточным центром вращения т.B  т.B  т.B2

L

L 1      b ₁

т. B ' т. B‘' т . B '

Уравнение движения системы при использовании координаты у имеет вид: y • { p ² • [ m + m '( i ' ) ² + Li 2 + L ( i ' ) ² ] + p [ bi 2 + b ( i ' ) ² ] + ki 2 + k_x( i ' ) ² } =

= z 1 •<

[ - m '• i '• ( l - i ' ) - L₃ i ₃ • ( I - i ₃) + L_xi '• ( l + i ' )] • p ² +

+ p • [ — bi^ • ( 1 — i ₂) + b_x • i ' • ( 1 + i ' )] + k_xi ' • ( 1 + i ' ) — ki ( 1 — i_x ) + z • [ Li₃p ² + bi ₂ + ki ] + z 2 • [ — L_xi₃p ² — b • i ' p — k_x • i_x ].

H

Объект защиты, как следует из структурных моделей, отображается интегрирующим звеном второго порядка; на вход звена подается усилие, а выходным сигналом является смещение. Такая структурная интерпретация и функциональные различия между типовыми элементами структурной схемы исходной механической колебательной системой объясняются особенностями аналитического аппарата теории автоматического управления [1]. Что касается свойств массоинерционных элементов, то они могут проявляться в двух формах: массоинерционный элемент является объектом защиты (или управления) либо массоинерционный элемент работает как типовой элемент аналогично упругим и диссипативным звеньям.

Способом расширения набора типовых элементов может рассматриваться введение дополнительных связей, реализуемых различными механизмами.

В [7, 8] показано, что в математическом виде свойства дополнительных связей (или механизмов) интерпретируются типовым звеном, реализующим функции дифференцирующего звена второго порядка. Дальнейшее усложнение дополнительных связей, вводимых в базовую схему, приводит к структурам, которые имеют передаточные функции в виде дробно-рациональных выражений, что позволяет даже в простых моделях отображать сложные динамические взаимодействия реальных технических объектов с пространственной метрикой.

Характерными особенностями расчетных базовых схем виброзащиты с угловыми колебаниями является наличие рычага, имеющего пространственные размеры, поэтому существенное значение приобретают координаты точек закрепления типовых элементов, что формирует динамические взаимодействия, зависящие от геометрических параметров. Значимую роль приобретает и форма рычага, что предопределяет расположение элементов не только с одной стороны, но и с двух сторон от точки вращения, а это обеспечивает при суммировании силовых факторов возможности взаимной компенсации.

Исходная модель может быть трансформирована, если технический объект достаточно сложен и при его упрощениях приходится учитывать ряд конструктивно-технических особенностей (рис. 4) [2, 9, 10].

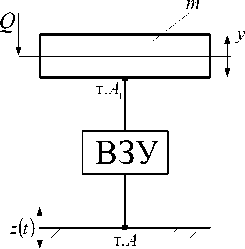
В точках контакта ВЗУ (рис. 4 а) с объектом защиты (т. А 1 ) и опорной поверхностью возникают динамические реакции. Кроме динамических в т. А , А 1 возникают и статические реакции, вызванные постоянными силами, в том числе силами тяжести объекта (и элементов ВЗУ). В общем случае реакции в т. А и А 1 не равны друг другу. К элементам ВЗУ также могут прикладываться внешние возмущения.

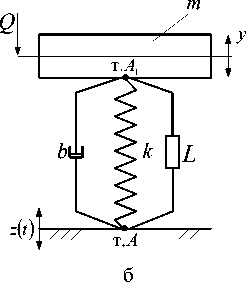
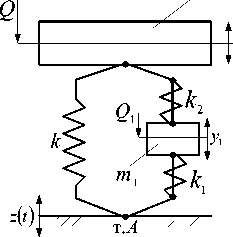
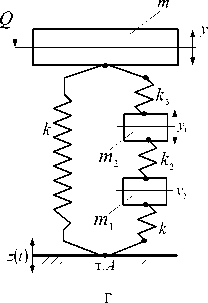
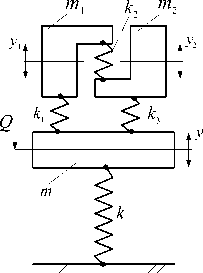
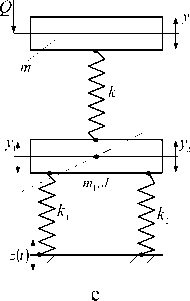
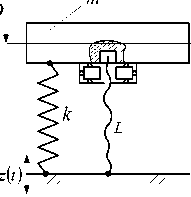
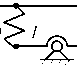
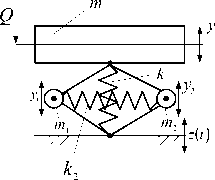
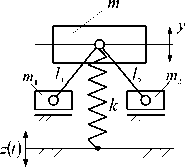
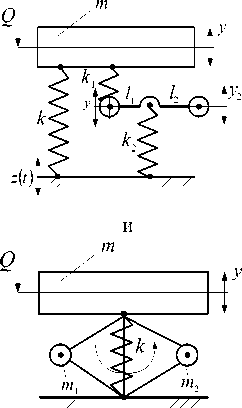
В простейшем виде ВЗУ может быть представлено (набором или поодиночке) типовыми элементарными звеньями в виде пружин, демпферов и устройств для преобразования движения, имеющих простые передаточные функции усилительного звена, а также дифференцирующих звеньев первого и второго порядков (рис. 4 б). Введение в структуру виброзащитной системы или в состав ВЗУ колебательных контуров (рис. 4 в-е) расширяет возможности решения задач вибрационной защиты за счет формирования дополнительных режимов динамического гашения колебаний [3, 4]. Введение механизмов в структуру виброзащитных систем в виде механизмов различных конструктивно-технических форм (рис. 4 и-м) достаточно подробно освещено в работах авторов [6-8], ряд конструктивно-технических предложений защищены российскими патентами [9, 10].

а

m

в

д

m

k

l ₂   ^m 2   y 2

y

k ₂

ж

з

л

м

Рис. 4. Варианты конструктивно-технического оформления виброзащитных устройств (ВЗУ) в системе поступательного прямолинейного движения объекта защиты с одной степенью свободы: а ‒ расчетная схема обобщенного вида; б ‒ виброзащитное устройство (ВЗУ) представлено типовыми элементами расширенного набора [5]; в ‒ ВЗУ имеет в своем составе колебательный контур m1, k1, k2; г ‒ ВЗУ имеет колебательный контур с двумя степенями свободы; д, е ‒ ВЗУ с колебательным контуром в виде замкнутой механической цепи; ж ‒ ВЗУ содержит винтовой несамотормозящийся механизм L; з ‒ ВЗУ имеет рычажный механизм с неподвижной опорой;

и ‒ ВЗУ с подпружиненной точкой опоры; к ‒ ВЗУ с рычажно-шарнирным механизмом; л ‒ ВЗУ с механизмами, имеющими поступательные кинематические пары; м ‒ ВЗУ с вращающимся шарнирно-рычажным механизмом

Заключение

Приведенные результаты составляют первую часть результатов, в которых нашли отражение представления о возможностях обобщения понятия виброзащитного устройства (ВЗУ) до структуры, включающей не только известные в практике пружины и демпферы, но и другие устройства. Такие устройства обеспечивают преобразование движения элементов системы, формируют систему их взаимного расположения в пространстве и создают новые динамические режимы. Виброзащитные устройства в такой постановке могут быть представлены различными механизмами, совершающими в составе структуры малые колебания относительно положения статического равновесия, т.е. от исходной конфигурации. При этом настроечные возможности ВЗУ определяются конструктивными особенностями механизмов.

Исследования выполнены по гранту в рамках Федеральной целевой программы «Научные и педагогические кадры инновационной России» на 2012–2013 гг. по теме «Мехатроника виброзащитных систем» (1.3.2. – естественные науки) № 14.132.21.1362.