Мета-анализ демографической реакции населения разных стран на распространение коронавируса COVID-19

Начавшаяся в конце 2019 г. в Китае эпидемия коронавируса COVID-19 (SARS-CoV-2) в течение 2020 г. переросла в пандемию и охватила все страны мира, оказав влияние на состояние экологии, экономики и социально-демографические характеристики жизни населения. Несмотря на предпринятые меры по изоляции, вакцинации и карантинные ограничения, пандемическая ситуация в мире в конце 2021 — начале 2022 гг. вновь обострилась. Ответная реакция общества и государства на эти события отличается в разных странах, как по особенностям принимаемых правительствами решений по управлению эпидемической ситуацией, так и по изменению популяционного здоровья населения, которое определяется многими факторами, включая генетическое, природно-климатическое и социально-экономическое влияние [1]. Подчеркивается, что пандемия — не только медицинское явление, а колоссальное воздействие на общество, приводящее к обострению социальных проблем [2]. Коллективная реакция (отклик, ответ, эффект, последствия) на такие воздействия населения выражается в изменении демографических характеристик под влиянием внешних факторов различной природы, особенно в кризисных ситуациях, к числу которых относятся риски и опасности, связанные с пандемией COVID-19 [3].

Количественные исследования реакции населения разных регионов и стран мира на инфицирование базируются на материалах статистической отчетности о числе подтверждённых случаев заболевания, выздоровления и смертности от COVID-19, которое отображает новые аспекты популяционной динамики [4; 5]. Демографическая реакция на изменение ситуации вследствие естественных причин и действий государственной власти может служить показателями оценки опасности и риска распространения инфекции, эффективности управления и особенностей поведения населения [6], подкреплённые данными социологических опросов [7]. Используемые в опросах анке- ты включают сведения о демографических показателях, владении знаниями об особенностях заболевания, по используемым источникам информации о вирусе, о следовании мерам предупреждения распространения болезни, трудностях, с которыми сталкивались респонденты в связи с пандемией [8]. Оценивались психосоциальные послед -ствия пандемии, связанные с закрытием образовательных учреждений, переходом на онлайн-обучение, изоляцией и иными карантинными мерами и так далее.

Многие социологические исследования касаются вопросов психологической нагрузки на людей в условиях пандемии COVID-19 [9]. Выявлено, что проживающие в городе, имели меньший уровень беспокойства, чем жители сельской местности, что связывается с различием уровня экономического развития, доступности культурных и образовательных ресурсов. Показано, что в богатых странах люди более тревожно реагируют на пандемию, чем в бедных, например, в Латинской Америке [10]. Следовательно, пандемия помимо высокого риска потери работы, физического здоровья и жизни, глобально повлияла на психическое здоровье населения. Пандемия COVID-19 привела к повышению беспокойства и тревожности населения всего мира, проявилась в реакции людей на разных уровнях от отдельного человека до населения стран; при этом эпидемический процесс статистически оценивается в показателях заболевания, вакцинирования, выздоровления и смертности.

С целью объединения результатов исследований разных территорий, обоснования и проверки научных гипотез предлагается использовать методы географического мета-анализа [11], которые в приложении к оценке демографической реакции населения разных стран на распространение заболевания COVID-19 позволят выявить общие закономерности эпидемического процесса [5] и представить их в форме математической модели его поэтапного развития для решения прямых и обратных задач моделирования и прогнозирования возникновения кризисных ситуаций.

Мета-анализ в научных исследованиях

Под мета-анализом понимается совокупность процедур сквозной научной методологии, заключающейся в объединении результатов ряда исследований методами статистики для проверки одной или нескольких взаимосвязанных научных гипотез. Мета-знание — чистое знание, абстрагированное от местных обстоятельств, территориальных особенностей. Высокая общность подхода, его междисциплинарный характер и учет условий среды позволяет рассматривать методологию мета-анализа на метатеоретическом уровне, предполагающем использование математических формул отображения знаний с фундаментальными содержательными ограничениями [11]. Наиболее широкое применение метаанализ нашёл в социальных, медицинских и биологических науках [12; 13], где он используется с целью выявления общих закономерностей, изучения и объяснения наблюдаемых различий вследствие неоднородности (гетерогенности) результатов исследований и, соответственно, увеличения точности оценки эффекта анализируемого вмешательства с применением статистической обработки имеющейся информации. Это позволяет более точно определять категории объектов и типы среды, для которых применимы полученные результаты [11].

Методология мета-анализа базируется на метатеоретической основе — гипотезе системного расслоения земной реальности на многообразии геоисторической среды. Локально процессы и явления описываются однотипными квалиметрическими уравнениями интеграции и генерализации данных, поэтому каждая ситуация сводится к свойствам типового слоя и универсальным уравнениям связи переменных [11]. Это позволяет понимать и исследовать различные объекты как один и тот же объект, и сопоставлять их путем сравнения с выбранным эталоном. Проведение мета-анализа состоит из нескольких последовательных процедур-этапов, важнейшие из которых [14]: 1) определение критериев включения оригинальных исследований в мета-анализ; 2) оценка неоднородности их результатов; 3) получение обобщённой оценки величины эффекта (зависимости); 4) анализ чувствительности выводов.

Критерием включения информационных материалов в мета-анализ является однотипность решаемых задач и изучаемой зависимости F ( x ) — системной тематической модели, отражающей причинно-следственные связи в форме воздействия факторных переменных x = { x . } на реакцию F ( x ) похожих объектов. Базовая гипотеза проведения мета-анализа состоит в том, что поверхность, задаваемая функцией F ( x ) , является многообразием, т.е. локально подобна касательным в точке F ( x о ) , x о = { x о . } плоскостям (слоям) MTx о к этой поверхности, описываемым линейными соотношениями:

5 F       . .5 F . .

F ( x ) = a ■ x + F ( a ) = a ■ ( x - x ₀ ) + F ( x ₀ ), a • x = Xy x . , a i ( x ₀ ) ⁼ ^~ ( x _о ), _i x_i                   x_i

F * ( a ) = - a ■ x + F ( x ) = - ^IFx_Oi + F ( x ₀). ^{0       0}      “ 8 x.  ⁰ i       ⁰

Все наблюдаемые неоднородные явления F ( x ) рассматриваются как расслоения MT = { MTx о } над точками многообразия F ( x о ) параметров внешней и внутренней среды x о = { x о . } . В смещённых (относительных) показателях f ( y ) = F ( x ) - F ( x о ) , У = { y i } = { x . ~ x о . } функции F ( x ) локально соответствует однородное билинейное уравнение по переменным у = { у . } и a = { a . } :

⁹ f f ⁽ y ) = a • y = L ay, ^ - y . / i i - 9 y i i

Здесь f ( y ) — универсальная мета-аналитическая функция, одинаковая для всех средовых условий, позволяющая в локальных координатах y = { y i } сводить разные зависимости F ( x ) к одному типовому соотношению f ( y ) , сравнивать их путем сопоставления (отождествления) разных точек касания ( F ( x о ) , x о ) , характеризующих среду.

Коэффициенты чувствительности a = { a i } и F * ( a ) уравнения (1) определяются по статистическим данным с помощью линейного регрессионного анализа для каждого наблюдения. Оценка однородности разных выборок проводится путем сравнения F * ( a ) с линейной зависимостью (2). Коэффициенты корреляции R или детерминации R ² указывают при R = 1 на полную однородность статистических материалов различных наблюдений, т.е. подтверждают факт их проведения в однотипной среде с параметрами ( F ( x о ) , x о ) , которые вычисляются по данным разных наблюдений на основе регрессии F * ( a ) на все a i в соответствие с уравнением (2). Обобщённая оценка величины эффекта (зависимости) получается в виде универсальной формулы (3). Анализ чувствительности выводов мета-анализа проводится с изменением различных параметров уравнений (1)-(3) и оценочными расчётами реакций F ( x ) = f ( y ) + F ( x о ) для иных условий x о .

Для моделирования развития эпидемии обычно используются классическая и обобщённая эпидемиологические модели SIR У. Кермака и А. МакКендрика 1927 г. [15]. Она описывает перераспределение числа восприимчивых ( S ), инфицированных ( I ), умерших ( D ) и изолированных ( R ) частей населения со временем t . Одним из альтернативных направлений моделирования является оценка опасности и риска [6], что формализуется в терминах теории вероятности и надёжности. Надёжность связывается с отсутствием отказов (утрат, потерь, жертв, аварий) — свойством объекта сохранять его работоспособность (жизнедеятельность) во времени. В эпидемическом процессе отказ связан со случаями инфицирования, потерей здоровья или смертью человека. Надёжность отражает ситуацию в относительных показателях, в их ожидаемом осреднённом поведении.

Развитие эпидемии COVID-19 описывается функцией надёжности P * ( t ) — вероятности безотказной работы общественной системы, сохранения популяционного здоровья к моменту времени t . Текущее, реальное время t считается в днях с 1 января 2020 г. (рис. 1). Функция кумулятивной вероятности накопления отказов (ненадёжности) равна F * ( t ) = 1- P * ( t ) , и в эпидемиологической модели SIR S ( t ) = S _о P * ( t ) , I ( t ) = S _о F * ( t ) , где S _о — потенциал заражения, заранее неизвестное число возможно инфицированных. На основе функции надёжности P * ( t ) рассчитываются другие показатели:

P ( t ) ₌ _ dPM , E ( t ) ₌ ^-ln P * ( t ) , E * ( t ) ₌ ^-ln F * ( t ) , p ( t ) = dE =       ,

dt                                                            dt P ( t )

где P ( t ) - функция плотности вероятности (распределения) отказов, в частности, доля количества подтверждённых случаев инфицирования за единицу времени (сутки); E ( t ) , E * ( t ) — интегрированная опасность, вероятность того, что процесс будет E ( t ) или не будет E * ( t ) продолжаться до момента t ; p ( t ) - интенсивность отказов, дифференцированная опасность, или риск, равный доле заболевших за единицу времени в численности чувствительного населения S ( t ) (заболеваемость).

Показано [5], что пандемические кривые первой волны по качественным и количественным показателям лучше описываются функциями вероятности экстремальных событий — функцией Фреше распределения максимальных значений:

F * ( z ) = exp ( - z “ ) , z >  0, a> 0при z “ = ± exp [ - а ( т-т m ) ] ,

где T = 0 ln ( t / t m ) + t m — собственное время популяционной системы, 1/ 0 — константа временнóго растяжения графиков. Увеличение значения θ относительных темпов хода собственного времени τ приводит к сокращению длительности эпидемического периода, что индивидуализирует процесс по странам. В момент т = t m будет т = т m и в окрестностях точки t = t m собственное время τ линейно приближается текущим временем т = 0 1п ( t / t m ) + t m » 0 ( t / t m -1 ) + t m ; при 0 = t m величина т = t .

Функция плотности распределения равна

P ( t ) = a exp [ - а ( т-т m ) ] exp ^ -exp [ - а ( т - т m ) ] } .

Значение коэффициента а находится по положению т m ( t m ) = t m максимума функции P ( т m ) = P m : a = eP m . Кривая подтверждённых случаев заболевания за сутки P ( т ) согласно уравнению (6) сначала быстро возрастает, а затем медленно опускается. Прослеживается несколько эпидемических волн, каждая из которых аппроксимируется уравнением (6) (рис. 1) в данном случае в линейном приближении хода времени. Различие констант 0 влияет на величину коэффициента ы ^ ыО / t m в зависимости P ( t ) от времени t .

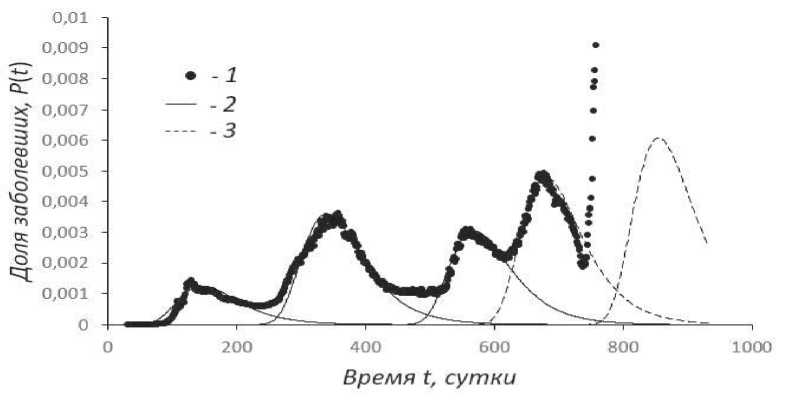
Рис. 1. Суточное изменение доли подтверждённых случаев заболевания СОVID-19 в России: 1 — исходные данные; 2 — кривые аппроксимации данных по формуле (6) при т = t; 3 — прогноз изменений при сохранении пандемической ситуации Fig. 1. Daily change in the proportion of COVID-19 confirmed cases in Russia: 1 — initial data; 2 — curves of data approximation according to the formula (6) when т = t ; 3 — forecast of changes while

maintaining the pandemic situation

Источник: ВОЗ: [сайт].— URL: (дата обращения: 30.10.2021).

Для функции Фреше интегрированная опасность E *( т ) = -In F * ( z ) = exp [ - а ( т - т m ) ] и риск заболеть (заболеваемость) p *( т ) = - dE *( т )/ d т=а ехр [ - а ( т - т m ) ] , где p * ( т m ) = а — приемлемый риск. Отсюда следует функция

P ( т ) / P m = eE *( т )ехр[- E *( т )],                             (7)

вид которой в координатах E *( т ) не зависит от средовых параметров ( т m , « ) , поэтому она может быть использована в процессе мета-анализа для выделения общих закономерностей. Нормированная кривая функции (7) проходит через начало координат (0, 0) при, E * ( t ) = 0 , F * ( т ) = 1 и точку максимума с координатами (1, 1) при E * ( т m ) = 1 .

Уравнения (4) для функции Фреше связаны с описанием механизма саморегулирования развития инфекционного процесса в показателях интегрированной опасности:

dE * ( т )/ d т = - a exp [ - а ( т - т m ) ] = - а E * ( т ), p *( т ) = а E * ( т ),                 ⁽⁸⁾

т.е. величины p*(т) и E *(т) пропорциональны с коэффициентом pm = а . Уравнение (8) показывает, как устойчивое уменьшение E *(т) с ходом времени т регулируется текущей опасностью инфицирования E *(т). Выражение p(т) = а.E *(т) является вариантом универсального уравнения (3) общего вида f (у )^ p (т)-pm = о[ E *(т)-E* (т m )] (9)

- линейной зависимостью риска и опасности заболеть. Этот факт может быть использован для оценки адекватности выбранной модели исходным данным и выявления степени изменчивости приемлемого риска p m = а по территориям.

Статистическая информация

Информационная основа исследования [5] базируется на статистических рядах данных по странам о фактах развития коронавирусной инфекции COVID-19, которые непрерывно формируются и хранятся в виде баз данных (БД) на нескольких международных серверах: сайты ВОЗ 1, Университета Джонса Хопкинса2 и Worldmeters.info3. Источником первичной информации являются тысячи официальных ресурсов о текущей ситуации по коронавирусу: правительств, министерств здравоохранения, региональных организаций, которые сопоставляются и верифицируются. В России сбор такой информации осуществляется через Министерство здравоохранения. Официальная статистическая информация по стране и отдельным регионам о количестве регистрируемых случаев заболевания, выздоровевших и умерших ежедневно публикуется на специальном сайте4. Содержание статистической информации о случаях заражения, выздоровления, летальности и др. зависит от орга- низации работы по её накоплению в каждой стране, поэтому оправдано применение в качестве показателей инфицирования относительных величин типа мер надёжности. Эффективность мета-анализа зависит от особенностей рядов эпидемиологических данных: есть гладкие ряды данных суточного прироста заболевших, удобные для обработки, и ряды данных с резкими изменениями значений, требующие предварительного сглаживания.

Данные по странам накапливаются и наглядно обрабатываются в электронных таблицах MS Excel по алгоритму описания статистического графика суточного прироста числа инфицированного COVID-19 населения за 2020-2022 годы. Рассчитывается вероятность потери здоровья (ненадёжности жизнедеятельности) чувствительным населением S о : F * ( t ) = S ( t ) / S о . В качестве S о принимается число заболевших на момент t (25.10.2021 г.) Вычисляется плотность распределения моментов заражения (подтверждённых случаев заболевания) — доля суточного прироста заболевших P ( t ) = F * ( t + 1 ) - F * ( t ) и другие показатели надёжности (2): интегрированная опасность E * ( t ) = -ln F * ( t ) ,риск p ( t ) = E * ( t + 1 ) - E * ( t ) . Суточные данные по плотности распределения доли заболевших P ( t ) по странам подставляются в таблицу MS Excel, и автоматически рассчитываются коэффициенты модели и кривые аппроксимации.

По информации 2020 г. выявлен индивидуальный характер динамики заболевания населения разных стран, выраженный в количественных показателях подготовленности и управляемости эпидемической ситуацией. По показателю опасности ln E ( t ) развития эпидемии коронавируса выясняется, что по сравнению с другими странами население России слабо реагирует на пандемическую ситуацию и не в полной мере осознаёт необходимость соблюдения мер противодействия эпидемии, и требуется введение более строгих мер профилактики [6].

Уточнение вида модели в терминах теории надёжности и проверка ее на массовом материале показали, что лучшую аппроксимацию кривых роста доли инфицированных обеспечивает функция Фреше (5) распределения максимальных значений, в данном случае — моментов t подтверждения случаев заболевания. По данным первой (весенне-летней) волны развития пандемического процесса 2020 г. по странам продемонстрировано существование двух связанных а = eP m показателей приемлемого риска а = 0,026/сутки и максимума P m = 0,0095/сутки кривой плотности распределения P ( t ) ежесуточного заражения по моментам времени t , величина которых одинаковая по территориям [5]. Это означает, что развитие пандемии по странам относится к одному типу явлений, что позволяет привести зависимость P ( t ) к одной типовой мета-аналитической модели P ( т ) с постоянными коэффициентами.

Четвёртая волна пандемии коронавируса COVID-19 осенью 2021 г. в России и во всем мире проходила на фоне сложной политико-экономической ситуации с особенностями, связанными с вакцинацией и появлением новых штаммов коронавируса, при заражении которыми болезнь быстрее развивается с сокращённым инкубационным периодом до 4,5-5 дней и быстрым утяжелением клинических проявлений в течение нескольких дней после появления первых симптомов. Больные стали более заразными и могут инфицировать больше людей, которые сами легче заражаются. Среди тяжёлых пациентов, которых не удаётся спасти, появились молодые люди старше 30 лет, у которых нет хронических заболеваний. Медики отмечают, что в красных зонах мало пациентов, которые сделали прививку — среди них умирают единицы с хроническими заболеваниями и солидным возрастом. Врачи считают, что в России практически не было серьезных ковидных ограничений, поэтому заболеваемость и смертность стремительно растут5.

Подъем пятой волны пандемии в России состоялся в середине января 2022 г. и связан с омикрон-штаммом SARS-CoV-2. Заболевание протекает легче или так же, как при заражении дельта-штаммом, но поражаются переболевшие и вакцинированные, дети и молодежь. Его быстрое распространение приводит к дополнительной нагрузке на систему здравоохранения. По данным статистики на 25.10.2021 число заболевших в России равно I=8,2 млн человек, умерших от COVID-19 — D =227,5 тыс. человек, т.е. летальность в среднем составила D/I=0,0279. С января 2021 г. летальность увеличилась почти в 2 раза с 1,87 до 3,60%, что совпало с началом массовой вакцинации и объясняется ростом тяжести заболевания по разным причинам. Летальность оказалась выше в 4 раза среди непривитых от коронавируса, чем вакцинированных. Общая смертность возросла на 18% по сравнению с прошлым годом. С января 2022 г. текущая летальность резко сократилась до 1,04%.

Мета-анализ рядов данных

Мета-зависимость (9) в виде p ( т ) = а Е * ( т ) + р достоверно проявляется в реакции населения РФ и удовлетворяет формуле (9) p ( т ) = 0,0217 Е *( т )-0,0169 с коэффициентом корреляции R=0,919. Коэффициент а = 0,0218 соответствует мере приемлемого риска, которая изменяется по странам, и в 24 из них при R>0,7 рассчитанный интервал а = 0,02270 ± 00178 включает значение а по России. В общем случае коэффициент а варьирует по странам и континентам р = -0,988 а + 0,00497 (R=0,761) согласно соотношению (2), когда по аналогии с уравнениями (1) и (9):

p ( т ) - 0,00497 = а [ Е * ( т ) - 0,988], (10)

то есть а является переменной величиной, когда зависимость p ( т ) от Е *( т ) представляет собой пучок линий с наклоном α по каждой стране и ситуации. Центр пучка [ p ( г m ) , Е * ( г m ) ] находится в точке [ 0,00497;0,988 ] . Уменьшение значения а соответствует увеличению длительности волны эпидемического процесса. Центральное положение соответствует Е * ( т m ) к 1 .

По формуле (7) нормированное значение P ( т ) отношением P n ( т ) = P ( т )/ P m в идеальном варианте должно определяться только величиной интегрированной опасности Е *( т ) . Для кривых отдельных волн эпидемии для приведения к общему виду эта величина трансформируется Е *( т ) ^ e *( т ) для каждой страны так, чтобы графики проходили через начало координат (0, 0), когда нормированное значение e *( т ) = 0 , и точку максимума (1,1) при P ( т ) / P m = 1 и e * ( т ) = 1 . Общее для всех стран уравнение преобразования e *( т ) = [1,61 Е *( т ) - 0,78] ’ , у = 1,45 показывает, что линейная при у = 1 зависимость (7) в общем случае нелинейна у = 1,45 , т.е. имеет место взаимодействие показателей опасности Е * ( т ) , обычно связанное с положительным эффектом самоорганизации.

Графическая зависимость P n ( т ) = P ( т ) / P m от e *( т ) (рис. 2) значений для отдельных стран соответствует расчетной кривой P n [ e * ] вида (7). Выявляется сходство графиков P n [ e * ] для населения разных стран (рис. 2в), что позволяет рассматривать разные зависимости (рис. 2а, б) как единую мета-закономерность, которая удовлетворяет уравнению (7) для нормированных значений Е *( т ) ^ e *( т ) и учитывает 94% точек на графике. Для России сходство эмпирических и теоретических показателей зависимости P n [ e * ] очень высокое (R=0,97).

При проведении мета-анализа происходит сжатие информации с выделением постоянных коэффициентов и общих закономерностей связи характеристик систем в «чистом» виде в центральной информативной части рядов данных одной волны. Минимальный разброс (однородность) данных вокруг графиков теоретических формул опре- деляет достоверность связей и позволяет их использовать в различных условиях для обработки рядов данных и решения задач прогнозирования. Графики на рис. 2 подтверждают работоспособность формулы (7), а значит и уравнений (5) и (6) в статистических исследованиях, но не обязательно их окончательно обосновывает, поскольку рекомендуемый вид формулы E *(т) = exp[-а(т - тm)] может быть иной. Подтверждением формулы становится линейная зависимость lnE *(т) = -а(т - тm) = -а.т + атm .

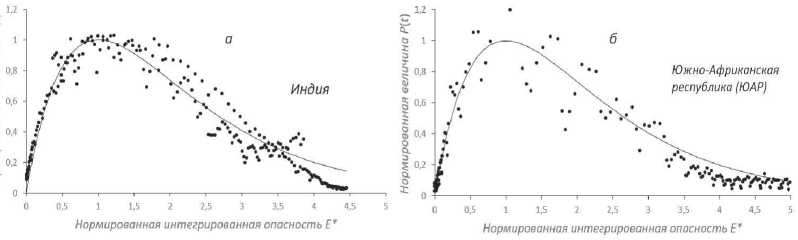
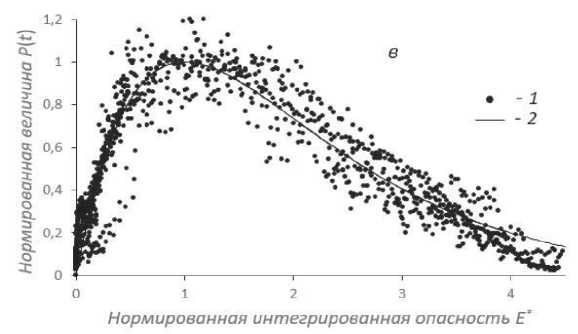
Рис. 2. Точечные графики зависимости нормированной доли P n ( т ) = P ( т )/ P m!

подтверждённых случаев второй волны заболевания коронавирусом СОVID-19 от величины е* ( т ) нормированной интегрированной опасности E* ( т ) в Индии (а) и ЮАР (б), а также с наложением графиков (в) для разных стран (Россия, США, ЮАР, Мексика, Индия, Казахстан, Канада): 1 — исходные данные; 2 — кривая аппроксимации данных по формуле (7).

Fig. 2. The dot plots of the dependence of the normalized proportion Pn(t) = P(t) / Pm of confirmed cases of the second wave of COVID-19 coronavirus disease on the value of e * (т) of standardized integrated hazard E * (т) in India (a) and South Africa (б), as well as with overlapping graphs of different countries (Russia, USA, South Africa, Mexico, India, Kazakhstan, Canada): 1 — initial data; 2 — the curve of data approximation according to the formula (7). Источник: по данным Информационного центра Университета Джона Хопкинса по коронавирусу: [сайт].— URL: (дата обращения: 30.10.2021).

В частности, для населения России при т = t в период первой волны пандемии получается ln E *( т ) = -0,0217 т + 4,072 , т m = 188 дней, R=0,99. Здесь коэффициент а = 0,0217 совпадает по значению с величиной, полученный по формуле (9) для российских рядов данных. Такое сходство просматривается и для других стран, что позволяет использовать уравнение (6) для дальнейших расчётов.

Для вычисления доли подтверждённых случаев заболевания коронавирусом COVID-19 в России Р к ( t ) (см. рис. 1) для каждой эпидемической волны к применяется уравнение (6) в реальном времени т = t с поправкой К к на амплитуду волны: P k ( t ) = K k P ( t ) . Коэффициенты уравнения равны а = 0,0217 и P m = 0,008 . Расположение сезонных пиков т m = t mk доли заболевших различается примерно на 179 дней, т.е. на полгода. Для прогнозирования необходимо заранее знать величину К к и расположение t mk (модальные значения) пиков инфицирования, что примерно определяется по тенденциям их роста: t mk = 170 к , К к = 0,139 к . В итоге появляется возможность рассчитать эпидемические кривые (см.рис.1), основываясь на мета-аналитической формуле (6) Р ( t ) = Р к ( t ) / К к с поправками на амплитуду К к и расположение t mk пиков эпидемических волн.

На рис. 1 показаны первые 4 волны эпидемии COVID-19 в России за два года и начало пятой волны: наблюдаемые данные и прогнозные расчеты демографической реакции населения, выполненные по уравнению (6). Расчеты (пунктирная кривая рис. 1) проводились на момент 25.10.2021 г. (666 день наблюдения) и до начала января 2022 г. подтверждались текущей статистикой по заболеваемости COVID-19. Однако с 14.01.2022 г. (747 день) тенденция нарушилась в связи с появлением нового омикрон-штамма коронавируса, эпидемия которого и по времени начала и по масштабу проявления коренным образом отличается.

Выводы

Кривые, описывающие реакцию населения разных стран на распространение коронавируса COVID-19, имеют различающуюся временную структуру, в которой проявляются скрытые мета-аналитические закономерности. Это позволяет рассматривать различные графики как один и тот же график, сопоставлять кривые путем сравнения их с эталоном, в качестве которого могут использоваться ряды данных по заболеваемости населения РФ. Метатеоретической основой мета-анализа является методология расслоения многообразия связей переменных, характеризующих ситуацию — разделения объектов по условиям среды реализации этих связей в различных временных и пространственных обстоятельствах. В каждом ситуационном слое эпидемические кривые описываются функциями надёжности — вероятности проявления экстремальных событий, а именно, — функцией Фреше распределения максимальных значений. Функция удовлетворяет дифференциальному уравнению, отражающему процесс саморегулирования ситуации в показателях изменения опасности заболевания населения и может быть уточнена с учетом нелинейного эффекта самоорганизации. Кривые инфицирования послойно сравниваются путём сопоставления модальных значений: временного расположения пиков эпидемических волн и их амплитуды по разным странам.

Статистическая проверка гипотез мета-анализа указывают на достоверность теоретической связи риска заразиться с опасностью заболеть коронавирусом COVID-19 и зависимости нормированной доли подтверждённых случаев заболевания в разных странах от интегрированной опасности. Эти связи позволяют аналитически аппроксимировать ряды данных и разрабатывать прогнозы развития пандемии, основы- ваясь на знании тенденций роста амплитуды и изменения положения волн эпидемического процесса. Мета-аналитические исследования направлены на выявление общих закономерностей в разнородных проявлениях этого процесса, получение функциональной оценки величины эффекта (зависимости), показывающей, что население разных стран одинаково реагирует на опасность. В исследовании представлена общая схема мета-анализа, которая необходима для дальнейшей обработки большого постоянно обновляющегося массива пространственно-временных эпидемиологических данных.

Практически решается обратная задача моделирования — выявление скрытых закономерностей развития пандемии для поиска мета-аналитического механизма регулирования, необходимого в разных странах для управления критической ситуацией, мерой сложности которой становится операционная единица, соответствующая опасности ситуации, что имеет важное значение для информационного обеспечения устойчивого развития общества.