Metagraph theory as a basis for modeling relevant media discourse

DOI:

Since the term “modeling” has a fairly broad meaning, note that in this article, by modeling, we will understand the use of a data model that allows representing and analyzing a media discourse.

The task of developing a data model for the formalization of textual and media discourse has been considered for a long time. The most well-known solution in this area is Mann and Thompson’s Rhetorical Structure Theory (RST) [Feng, 2023].

Currently, neural network solutions are mainly used for natural language processing, in which vector embeddings are used as a text representation model [Pilehvar, Camacho-Collados, 2020].

In particular, approaches such as word2vec and Glove are used to construct vectors of individual words, and the doc2vec approach is used to construct vectors of documents (text fragments) [Pilehvar, Camacho-Collados, 2020]. Explicit conversion of word vectors into text fragment vectors is not possible (this task requires building a separate model). Thus, the use of neural network models does not simplify the task of discourse modeling.

Currently, Large Language Models (LLM) are increasingly used for text analysis [Minaee et al., 2024]. At first glance, it may seem that the emergence of LLM models allows us to completely solve the problem of discourse modeling. The LLM model is capable of answering questions about the text, finding connections between text fragments and performing other complex actions on texts using the prompts mechanism (there is no need to go down to the level of vector embeddings). But the LLM model cannot be considered as a reliable discourse model, due to the fact that it is susceptible to hallucinations, which are features of model training and are difficult to diagnose and eliminate in practice [Yao et al., 2023].

Thus, despite significant advances in the field of neural network text processing, the task of modeling text and media discourse remains relevant.

In most of the previously proposed classical approaches, the task of modeling media discourse is reduced either to manipulating logical variables or to constructing a flat graph based on text fragments.

In this article the approach based on combination of a complex graph model and a multidimensional model is proposed.

The term “complex” in relation to graph models causes the greatest controversy. As a rule, the term “complex” is interpreted in two ways.

Option 1. Flat graphs (networks) of very large dimension. Such networks can include millions or more vertices. Edges connecting vertices can be undirected or directed. Sometimes a multigraph model is used, in which case two vertices can be connected not by one, but by several edges.

Option 2. Complex graphs that use a complex description of vertices, edges and/or their locations. Often in such models they abandon the flat arrangement of vertices and edges. It is these types of models that can be most useful when describing complex data models. Today, three version of complex graph models are known: hypergraph, hypernetwork, and metagraph. It is the metagraph model that is the most flexible and can be actively used for modeling complex subject areas, including in the humanities.

The core element of a metagraph model is a metavertex, which can include nested vertices, edges, and metavertices. The presence of metavertices with their own attributes and connections with other vertices is an important feature of metagraphs. This corresponds to the principle of emergence that is, giving the concept a new quality, the irreducibility of the concept to the sum of its component parts.

An extension of the metagraph model is a multidimensional metagraph model, which, using an OLAP-like approach, allows storing not just numerical data in hypercube cells, but descriptions of complex situations in metagraph form and process situations when convolving hypercube fragments.

It is a multidimensional metagraph model that is used in this article for representation of discourse based on various media.

Materials and ьethods

In this section, we will briefly consider the basics of the metagraph model, the multidimensional metagraph model and their capabilities for modeling media discourse.

The metagraph model was initially proposed by A. Basu and R. Blanning in 2007 [Basu, Blanning, 2007], the model later received a number of extensions independently offered by various groups of researchers. Further in the article, by the metagraph model, we will understand the annotating metagraph model that is discussed in detail in [Gapanyuk, 2021].

The Brief Definition of the Annotating Metagraph Model. The metagraph may be described as follows: MG = V , MV , E , ME} , where MG – metagraph; V – set of metagraph vertices; MV – set of metagraph metavertices; E – set of metagraph edges; ME – set of metagraph metaedges.

Metagraph vertex is described by a set of attributes: v_i = { atr k } , v i e V , where v i - metagraph vertex; atr_k – attribute.

Metagraph edge is described by a set of attributes, the source, and destination vertices:

e_i = v s , , v E , { atr k }) , e i e E , where e i - metagraph edge; v_S – source vertex (metavertex) of the edge; v_E – destination vertex (metavertex) of the edge; atr_k – attribute.

The metagraph fragment: MG i = { ev j } , ev j e ( V о E о MV о ME ), where MG i - metagraph fragment; ev_j – an element that belongs to the union of vertices, edges, metavertices, and metaedges of metagraph.

The metagraph metavertex: mv i = ({ atr k } , MG j , mv i e MV , where mv i - metagraph metavertex belongs to a set of metagraph metavertices MV ; atr_k – attribute, MG_j – metagraph fragment.

Thus, metavertex, in addition to the attributes, includes a fragment of the metagraph. The presence of private attributes and connections for metavertex is a distinguishing feature of the metagraph. It makes the definition of metagraph holonic – metavertex may include a number of lower-level elements and, in turn, may be included in a number of higher-level elements.

The proposed kind of metagraph model is called the annotating metagraph model because the same set of vertices and edges can be included in several different metavertices, which can represent different situations and can be annotated with different attributes. In other versions of the metagraph model, such metavertices were forcibly combined into single metavertex.

The example of metagraph is shown in Figure 1. The example contains three metavertices: mv₁ , mv_{2 ,} and mv₃ . Metavertex mv₁ contains vertices v₁ , v₂ , v₃ and connecting them edges e₁ , e₂ , e₃ .

Metavertices mv₂ and mv₂ ’ contains vertices v₄ , v_{5 ,} and connecting them edge e₆ . The identical

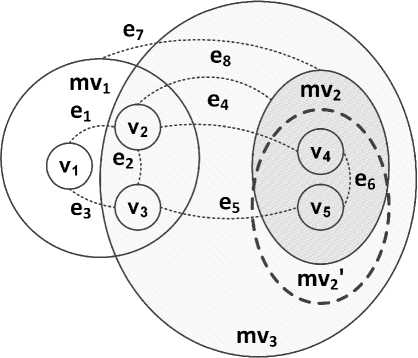
Fig. 1. The example of metagraph

contents of the metavertices mv₂ and mv₂ ’ emphasize the annotating feature of the proposed model.

Edges e₄ , e₅ are examples of edges connecting vertices v₂-v₄ and v₃-v₅ are contained in different metavertices mv₁ and mv₂ .

Edge e₇ is an example of the edge connecting metavertices mv₁ and mv₂ .

Edge e₈ is an example of the edge connecting vertex v₂ and metavertex mv₂. Metavertex mv₃ contains metavertices mv₂ and mv₂ ’ vertices v₂ , v_{3 ,} and edge e₂ from metavertex mv₁ and also edges e₄ , e₅ , e_{8 ,} showing the holonic nature of the metagraph structure.

Thus, in the metagraph model, a metavertex can contain both vertices and edges.

The vertices, edges, and metavertices are used for data description while the metaedges are used for process description. The metagraph metaedge: mei= Vs,, vE ,{atr}, MGoD ’ mei e ME,MGORD = {MGj}, where mei -metagraph metaedge belongs to set of metagraph metaedges ME; vS – source vertex (metavertex) of the metaedge; vE – destination vertex (metavertex) of the metaedge; atrk – attribute, MGORD – ordered set of metagraph fragments MGj. Each metagraph fragment MGj can also contain nested metaedges, which makes the description of the metaedge recursive.

The example of a metaedge me1 is shown in Figure 2. The metaedge contains metavertices mvS, ... mvi, ... mvE and connecting them edges. The source metavertex contains a nested metagraph fragment. During the transition to the destination metavertex, the nested metagraph fragment became more complex, new vertices, edges, and inner metavertices may are added. In case of Figure 2 the source metagraph fragment is sequentially annotated with metavertices mv2 and mv2’.

The Brief Definition of the Metagraph Agents. In order to ensure the transformation of metagraphs, metagraph agents ( ag^MG ) are used. Basically two kinds of metagraph agents are proposed: the metagraph function agent ( ag^F ) and the metagraph rule agent ( ag^R ). Thus, ag^MG = ag^F | ag^R .

The metagraph function agent serves as a function with input and output parameters in the form of metagraph: ag^F = MGG_m, MG_OUT, AST }, where ag^F – metagraph function agent; MG_IN – input parameter metagraph; MG_OUT – output parameter metagraph; AST – abstract syntax tree of metagraph function agent in the form of metagraph.

The metagraph rule agent is rule-based: ag R = MMG , R , AG^ST }, R = { r i } , r i : MG j ^ OP^MG , where ag^R – metagraph rule agent; MG – working metagraph, a metagraph on the basis of which the rules of the agent are performed; R – set of rules r_i ; AG^ST – start condition (either metagraph fragment for checking start rule, or start rule); MG_j – a metagraph fragment on the basis of which the rule is performed; OP^MG – set of actions performed on metagraph.

The antecedent of the rule is a condition over the metagraph fragment. The consequent of the rule is a set of actions performed on the metagraph.

Rules can be divided into open and closed.

The consequent of the open rule is not permitted to change the metagraph fragment

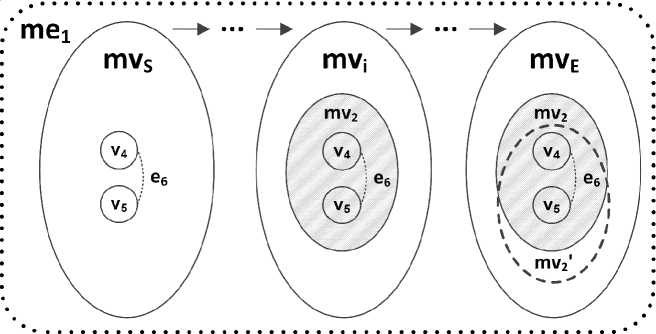
Fig. 2. The example of metaedge

occurring in the rule antecedent. In this case, the input and output metagraph fragments may be separated. The open rule is similar to the template that generates the output metagraph based on the input metagraph.

The consequent of the closed rule is permitted to change the metagraph fragment occurring in the rule antecedent. The metagraph fragment changing in rule consequent causes to trigger the antecedents of other rules bound to the same metagraph fragment. But incorrectly designed closed rules systems can cause an infinite loop of metagraph rule agents.

Thus, the metagraph rule agent can generate the output metagraph based on the input metagraph (using open rules) or can modify the single meta graph (using closed rules).

The Brief Formalization of the Multidimensional Data Model. The classical multidimensional data model, proposed by Edgar F. Codd, allows working with numerical data (measures) binding them to the hierarchical taxonomies (dimensions) [Codd, 1993]. The multidimensional data model is a core for OLAP (online analytical processing) information systems.

In this section, we use our own simplified version of the formalization of multidimensional data model according to [Gapanyuk, 2019], which will help to describe multidimensional metagraph model, proposed in the next section.

Multidimensional hypercube may be described as follows: HC = (MSR,HCD,HCF,HCR), MSR = { msr i } , HCD = { hcd i } , HCF = { hcf i } , HCR = { hcr i } , where HC - hypercube; MSR -set of hypercube measures ( msr_i – measure); HCD – set of hypercube dimensions ( hcd_i – dimension); HCF – set of hypercube facts ( hcf_i – fact); HCR – set of hypercube aggregation rules ( hcr_i – rule).

In the case of the classical multidimensional data model, it is assumed that a measure can store only numerical values.

Hypercube dimension: hcd i = { h hcd k } , ^, where hcd' k - hypercube dimension element; x -a partial order on the set of hypercube dimension elements. Partial order organization for dimension is more suitable than tree structure organization because partial order organization allows describing ragged hierarchies, in case of the time dimension, e.g. the “month ^ week ^ day” and

“month ^ decade ^ day” hierarchies are allowed to exist simultaneously in one dimension.

Hypercube fact: hcf j = ^{ hcd e } , { msr n }) , where hcd_i^ref – a reference to the dimension element; msr_n – measure. In the case of low-level hypercube fact, the set { hcd rf } contains references to low-level elements of all hypercube dimensions. In the case of aggregated hypercube fact { hcd rf } e P ( HCD ), the set { hcd' e } belongs to the powerset P of all hypercube dimensions because aggregation rules may exclude dimensions during the aggregation process. Simultaneously, during aggregation, elements hcd_i^ref roll up upon their hierarchies, providing data aggregation on higher levels of hierarchies.

Hypercube aggregation rule: hcr_k : { hcf OUT } = = agf ( { hcf _IN } , HCD ^ag ) , HCD ^ag c HCD , where hcf_OUT – output (aggregated) facts; agf – aggregation function; hcf_IN – input (nonaggregated) facts; HCD^ag – a subset of hypercube dimensions used in aggregation.

Aggregation rules allow calculating aggregated facts on the base of non-aggregated or low-level aggregated facts and hypercube dimensions. The typical aggregation functions are count , sum , min , max , and other numerical functions. Depending on the multidimensional system implementation, aggregation rules may be bound to the particular dimensions or the whole hypercube.

Today the multidimensional model is widely used. However, this model is oriented to numerical measures usage which may be considered as a significant limitation. Textual or object-oriented information is not considered for use as measures.

In [Gapanyuk, 2019] the multidimensional metagraph model is proposed which allows storing fragments of metagraphs in hypercube cells in order to overcome the limitations of the classical multidimensional model.

The Brief Formalization of the Multidimensional Metagraph Model. The formalization of the multidimensional metagraph model is based on the multidimensional data model formalization.

In this case the definition of a multidimensional metagraph hypercube remains the same: HC_MG = MSSR , HCD , HCF , HCR} , but the elements of all sets included in the definition acquire a metagraph interpretation.

The measure is considered as a metagraph fragment: msr = MG j where msr i - measure; MG_j – metagraph fragment. This means that a hypercube cell can contain not only a numeric value but any complex data structure described by the metagraph.

The hypercube dimension: hcd i (J hcd' k }, ^, hcd i e MV , hcd k е ( V и MV ), where hcd i -hypercube dimension; hcd_i ^k – hypercube dimension element; ч - a partial order on the set of hypercube dimension elements; MV – set of metagraph metavertices; V – set of metagraph vertices. The hypercube dimension may be represented in the form of a hierarchically organized metavertex. The hypercube dimension elements that correspond to leaves of the tree can be represented as vertices, while the elements of the higher levels as metavertices.

The hypercube fact: hcf j = ^ { hcd 'ef } , { msr n } ^ , hcd tf = e i , e i e E , msr n = MG j , where hcd tf -reference to the dimension element; msr_n – measure; e_i – metagraph edge that belongs to the set of metagraph edges E ; MG_j – metagraph fragment. The hypercube fact may be represented in form of metagraph. Measure is considered as a metagraph fragment. The reference to the dimension element may be represented as edge, connecting measure element and dimension element.

In the definition of the hypercube aggregation rule the metagraph agent (using open rules) is used in process of aggregation instead of aggregation function: hcr k : { hcf OUT } = = ag ( { hcf_m } , HCD ag ) , HCD ag a HCD , where hcf_OUT – output (aggregated) facts; ag^MG – the metagraph agent used for aggregation; hcf_IN – input (non-aggregated) facts; HCD^ag – the subset of hypercube dimensions used in aggregation.

The aggregation example is shown in Figure 3. There is a simple hypercube with two dimensions hcd₁ and hcd₂ . The hypercube facts correspond to the hypercube dimension elements combinations hcd₁¹¹-hcd₂¹¹ , hcd₁¹¹-hcd₂¹² , hcd₁¹²-hcd₂¹¹ , hcd₁¹²-hcd₂¹² are lower-level hypercube facts. The combination hcd₁¹-hcd₂¹ corresponds to the aggregated hypercube fact. In the process of aggregation, not only quantitative characteristics change but also the metagraph structure of cells corresponding to the facts of the hypercube.

Since, according to the definition, a measure is considered as a metagraph fragment, it is possible to create metaedges that are based on several cells of a hypercube. As an example, metaedge me₁ (firstly presented in Figure 2) is shown in Figure 3 as a dotted arrow.

Thus, the proposed approach allows storing in hypercube facts and aggregate not only numerical values but any complex data structures. This allows formally working with extracted from texts knowledge graphs.

The Metagraph-based Model of Text and Media Discourse. Based on multidimensional metagraph model the model of text discourse may be considered as multidimensional metagraph hypercube HC_MG .

The only service axis in a multidimensional hypercube is the “narrative time axis” or “model time axis”. The presence of this axis allows organizing the facts extracted from the text. Facts may or may not be linked to the realtime axis.

Example sentence: First unpack the laptop, then plug it into an outlet, then press the power button on the laptop.

This sentence contains three facts, ordered among themselves (using model time axis), but not linked to the real-time axis: unpacking the laptop, plugging it into an outlet, pressing the power button on the laptop.

An important issue is the construction of the axes of a multidimensional metagraph hypercube. The following three options can be offered for the construction of axes:

• –    “Axes construction 1”. Axis elements can be dynamically extracted from the text during its parsing;

• –    “Axes construction 2”. Pre-formed axes can be used that have been extracted from previously analyzed texts or created manually from thesauri;

• –    “Axes construction 3”. Pre-formed axes can be used, which are updated during text parsing.

From the point of view of the metagraph model, the following elements can be considered as metavertices:

• –    a separate axis of the hypercube;

• –    a fact extracted from the text;

• –    a fact linked to the axis elements characterizing it.

Consider the following example of two text fragments.

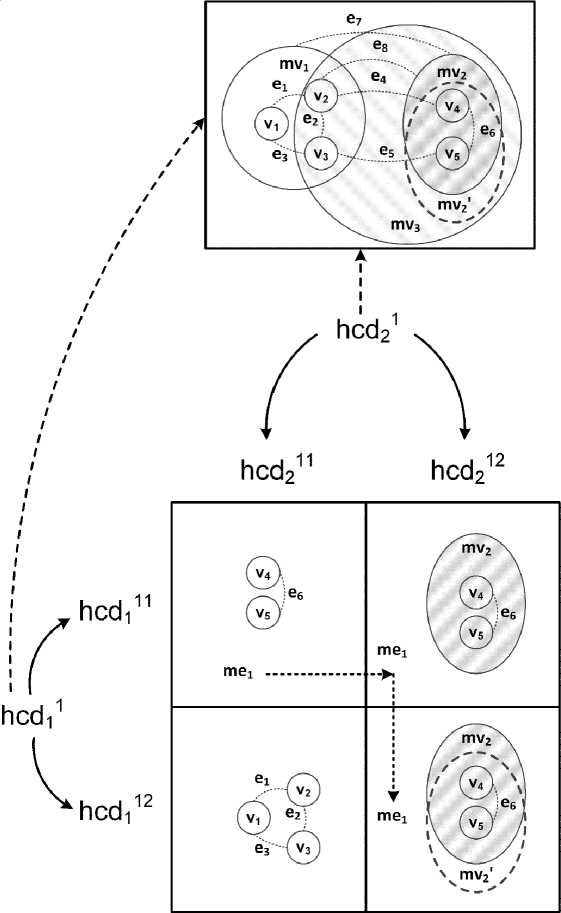
Fig. 3. The aggregation example

Text 1: In the morning the worker was repairing the window, and in the afternoon, he was repairing the roof.

Text 2: From 10 to 12 am, a worker strengthened the window frame using a screwdriver and self-tapping screws. From 14 to 16 pm, a worker was strengthening the roof using self-tapping screws and an electric screwdriver.

Both fragments consider a situation consisting of two facts: “a worker repairs a window”, “a worker repairs a roof”.

Using “Axes construction 1” approach we can extract the following axes from this text fragments:

Text 1:

• 1.    Time axis: “morning”, “afternoon”.

• 2.    Object axis: “window”, “roof”.

Text 2:

• 1.    Time axis: “from 10 to 12 am”, “from 14 to 16 pm”.

• 2.    Object axis: “window”, “roof”.

• 3.    Tool axis: “screwdriver”, “screws”, “electric screwdriver”.

Analyzing the axes of texts 1 and 2, we can draw the following conclusions:

• 1.    The object axis in both fragments is presented identically.

• 2.    The time axis in text 2 is considered in more detail than in text 1.

• 3.    Only text 2 contains elements of an instrumental axis.

Note that from the point of view of the metagraph model, the element “from 10 to 12 am” can be represented as a metavertex containing nested vertices of the beginning and end of work.

In general, the proposed approach allows solving the following problems:

– If different sources are evaluated, it is possible to understand whether their meanings are comparable by comparing the coincidence of the axes. If the axes of text 1 are a subset of the axes of text 2, then text 2 contains a qualitatively more detailed description of situations compared to text 1.

– For models constructed within the framework of coinciding axes, the following comparisons are possible:

• 1    . Comparison of generality/detail of descriptions (the most detailed descriptions correspond to leaf measurement concepts).

• 2.    Comparison of the order of facts (events) using the time dimension.

• 3.    Comparison of descriptions of the same situation obtained from different sources.

This approach can be used to analyze not only text discourse, but also media discourse. In this case, the multidimensional metagraph hypercube is extracted not from text, but from video (text captions can also be considered). The sequence of video frames naturally defines the “narrative time axis”.

In this case, each frame can be considered as a metavertex, and a sequence of frames as a metaedge.

The Architecture of a Metagraph Based Media Discourse Analysis System. The proposed approach can be implemented in the form of a media discourse analysis system. The architecture of this system is shown in Figure 4.

The kernel of the system is the multidimensional metagraph model storage, that is used for storing elements of the multidimensional metagraph model: axes and facts.

The system contains three large modules:

• 1.    The media parsing module.

• 2.    The text generation module.

• 3.    The metagraph modeling module.

The operation of the system consists of nine main steps (shown in Figure 4):

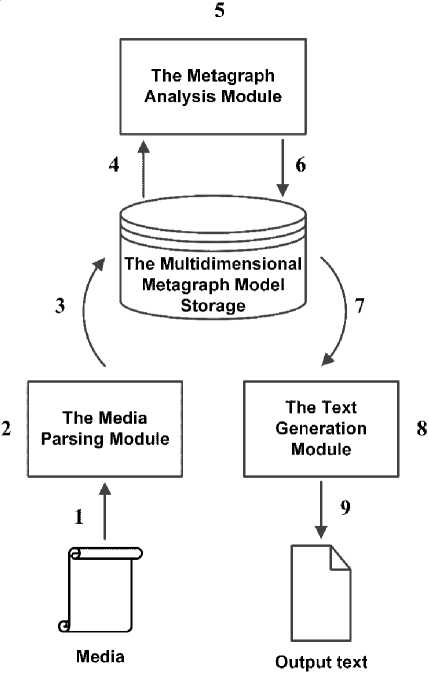
Fig. 4. The architecture of a metagraph based media discourse analysis system

• 1.    The media files are being prepared for parsing.

• 2.    The media files are parsed using deep learning methods. The elements of the multidimensional metagraph model are extracted.

• 3.    The extracted facts and axes elements are recorded into multidimensional metagraph model storage.

• 4.    The metagraph analysis module receives the data for analysis.

• 5.    The analysis is performed. The source fragments of metagraph are annotated with new metavertices. The output fragments of metagraph are created.

• 6.    The results of analysis are recorded into multidimensional metagraph model storage.

• 7.    The text generation module receives the destination metagraph fragment from the multidimensional metagraph model storage.

• 8.    The text generation module transforms destination metagraph fragment into text form.

• 9.    The output text document is generated.

An important feature of the system is that texts and video fragments in various languages can be considered as input data. The extracted metagraph fragments are combined into a single model in the multidimensional metagraph model storage.

Discussion

Formal models of discourse analysis is a topic that has been increasingly attracting the attention of researchers. A modern review of works on this topic is given in [Feng, 2023].

In particular, in [Feng, 2023], an approach based on the construction of logical predicates is revised in order to establish a causal relationship between the events under consideration. But the predicate-based approach is poorly designed to compare different text fragments with each other.

Also, in [Feng, 2023] the Rhetorical Structure Theory (RST) and the Cross-document Structure Theory (SCT) are considered.

In [Liu et al., 2019] it is noted that the Mann and Thompson’s Rhetorical Structure Theory (RST) “is one of the most influential theories of discourse, which posits a tree structure (called discourse tree or RS-tree) to represent a text.” [Liu et al., 2019, p. 2].

In [Liu et al., 2019], the issues of automated RST discourse construction using neural networks are mainly considered, and a more detailed description of the RST model is given in [Hou, Zhang, Fei, 2020].

According to [Hou, Zhang, Fei, 2020] the minimal unit in RST approach is “Elementary Discourse Unit” (EDU) which is “functionally a simple sentence or a clause in a complex sentence.” [Hou, Zhang, Fei, 2020, p. 2].

EDU are linked using Rhetorical Relation (RR) that “holds between two non-overlapping text spans and reflects how they link together to be a whole” [Hou, Zhang, Fei, 2020, p. 3]. The consistency of EDU linking is controlled by schemes (RST approach propose five kinds of schemes).

The Rhetorical Structure Tree (or RS-tree) is a “tree representation of a document under the framework of RST. The leaf nodes of an RS-tree are EDUs. Each internal node is characterized by a rhetorical relation and corresponds to a contiguous text span” [Hou, Zhang, Fei, 2020, p. 3].

From the point of view of the metagraph model, EDU may be represented as vertices and RR as edges. The RST model is based on flat graphs (tree graph model) and therefore, within the framework of this model it is impossible to describe such complex relationships as in the framework of the metagraph model. The consistency checking model (RTS schemes) may be implemented using metagraph agents.

The Cross-document Structure Theory (SCT) [Maziero, Jorge, Pardo, 2014] propose representing documents with levels: word level, phrase level, sentence/paragraph level, document level. Semantic links can be established between elements of all levels. The proposed hierarchy can be considered as an analogue of a set of nested metavertices. But the use of a multidimensional model is not proposed in this approach.

It is also necessary to mention such a project as Penn Discourse TreeBank (PDTB) which is now in version 3.0 [Webber et al., 2019]. This dataset contains about 53 thousand text fragments, as well as semantic links between them. The data model of this project is also flat graph, the disadvantages of which were already noted above.

Thus, in the reviewed sources, no approaches were found that, in order to formalize discourse, would simultaneously use a graph model (especially based on complex graphs) and a multidimensional model.

It should also be noted that the multidimensional metagraph model has a distant analogue that is called “Graph OLAP” [Schuetz, et al., 2021]. The main difference between the classical multidimensional model and the graph OLAP model is that instead of the hypercube aggregation operation, the graph aggregation operation is used [Khalil, Belaissaoui, 2022]. The Graph OLAP approach is an attempt to adapt the standard multidimensional model to graph data. This approach inherits the main problem of the classical multidimensional model. Unlike the multidimensional metagraph model, graph OLAP does not allow changing the type and structure of the data in the aggregation process, and therefore it is poorly suited for the discourse modelling.

Results

This article is based on a number of results obtained in the field of research of complex graphs, such as the annotating metagraph model, the metagraph agent approach, the multidimensional metagraph model.

The article shows that the multidimensional metagraph model can naturally be considered as a model of both text and media discourse.

At the same time, each analyzed media fragment should be simultaneously considered as both a metagraph of the situation representation and as a carrier of the set of axes elements of a multidimensional metagraph model. Axis elements can be dynamically extracted from the text during its parsing, or set of pre-formed axes can be used, or pre-formed axes can be updated during text parsing.

The proposed approach makes it possible to analyze and compare the discourses of several texts, while two fundamentally different cases can be distinguished: when the set of axes of a multidimensional metagraph model cube differs, and when it coincides. If the axes of text 1 are a subset of the axes of text 2, then text 2 contains a qualitatively more detailed description of situations compared to text 1. In case of coinciding axes, the following comparisons are possible: comparison of generality/detail of descriptions, comparison of the order of facts using the time dimension, comparison of descriptions of the same situation obtained from different sources.

Based on the multidimensional metagraph model, the architecture of a metagraph based media discourse analysis system is proposed. The usage of multidimensional metagraph model allows mixing information in different languages, initially presented both in text form and in video form (possibly using subtitles).

Conclusion

Based on the multidimensional metagraph model, the proposed approach allows storing and analyzing discourse presented in different languages and in various media forms.

The main drawback of the current version of the proposed model is the lack of a system of semantic checks of discourse, similar to schemes in RST. The designing of a system of such checks is the main direction for the development of further research.