Metal Artifact Reduction from Computed Tomography (CT) Images using Directional Restoration Filter

Published Online May 2014 in MECS

Now a day’s medical image processing is a most important task in diagnosis of diseases. Computed tomography (CT) [1] is highly noninvasive compared to other medical imaging modalities (e.g. Ultrasound imaging, Magnetic resonance). Unfortunately, CT image is corrupted by metal artifact when stent wire is used in cardiac functionalities. We are interested in metal artifact reduction in computed tomography (CT) reconstruction. The application subcontext is that of vascular imaging in the presence of a metal stent. Metal artifact reduction is one of the most important preprocessing tasks in the computed tomography processing field and it is a very complex and critical preprocessing step for feature extraction, segmentation, classification, registration from medical CT images.

Various artifact reduction techniques have been proposed, namely, statistical reconstruction algorithms [2] are more robust to the data inconsistencies that cause these artifacts. Most modern scanners implement various data preprocessing techniques to reduce these artifacts, many of which can amplify data noise [3]. [4] Used statistical reconstruction procedure on a sinogram that had been preprocessed by a metal artifact method. Moreover, metal artifact reduction by sinogram subtraction and simplistic interpolation may induce other artifacts in reconstructed images [5]. Many image denoising methods are proposed basis on wavelet, local statistics, contourlet transform, non-linear adaptive thresholding [6-34]. Extra-Energy Reduction (EER) [20] function is formulated based on local degree of unsmooth pixels in order to imperative results as well as create stable and equilibrium state in the entire images. Laplacian pyramid-base nonlinear diffusion (LPND) method [35] used for speckle reduction and edge preservation. The automatic determination of the gradient threshold used in the LPND. LPND method used MAD (Median Absolute Deviation) operator [36] for determination of the gradient threshold. An edge sensitive diffusion method [37] [i.e. speckle reducing anisotropic diffusion (SRAD)] is the speckle reducing anisotropic nonlinear diffusion filtering approach to spatial adaptive filtering as well as it demonstrates effective results of denoising in homogeneous regions in an image.

Our proposed method is based on the intersection fuzzy logic and iterative reconstruction in getting data set from the directional image data structure. The method does not require a lot of memory to run and does not require a lot of time to converge final consequences. The introducing method is more convenient for real life application and provides large amount of clinical benefits and faster algorithm for reducing metal artifact from CT images as well. The prime purpose of our investigated method is to reduce metal artifact from CT images.

This paper is structured as follows. In Section 2, the theoretical background of the proposed method, including structural representation of the filtering technique, is presented. Section 3 describes evaluation criteria for checking performance with other state-of-the-art algorithms (e.g. Perona-Malik (P-M) [34], SRAD [37], LPND [35] and EER [20]). Section 4 shows experimental visual results and graphical representation for performance testing. Section 5 offers concluding remarks.

• II.    Proposed Method

We proposed direction oriented iterative reconstruction filtering process with Fuzzy logic for reducing metal artifact from CT images. Our investigated method based on a fully automated intensity variation while iterative method is used for estimating metal artifact pixel values from the experimental images. We create two sets by iteration process and these sets will be sorted in ascending order. After sorting we take two elements from two data sets at the target point. The tracking both elements will be selected from the second position of those sorting arrays. Then Fuzzy intersection logic will be executed between two selected elements and Gaussian convolution operation will be performed in the entire image. In figure 1, we consider A and B direction oriented data sets which are generated from the original CT image I(x,y) , where image size is X X Y .

Set A is generated by following procedure:

r /2

A = R   I ^{( x} + i , y )                             (1)

i =- ( r /2)

And similarly set B is generated by following procedure:

r /2

B = R   I ( x , y + j )                          (2)

j =- ( r /2)

Where big- R is the iterative operator and it has been adopted and implemented in Real-Time Process Algebra (RTPA) [38] and r is the total number of element of the data sets in each step of filter execution. Where r = 5 and it is a positive odd integer number.

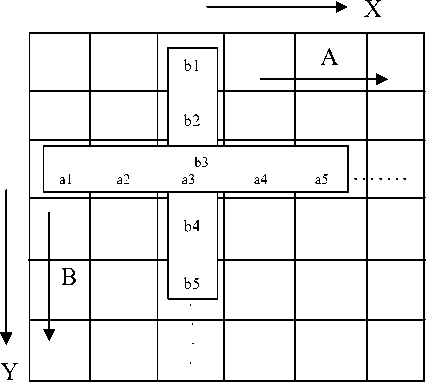
Fig. 1. structural representation of the filter mechanism

Now A and B are sorted data array in ascending order which are getting from A and B respectively. We track second position data element that are A_s (2) and B_s (2) . We apply intersection Fuzzy logic between A (2) and B (2) . If intersection Fuzzy set is C ,

M e ( t ) = ^mm ( M A, ⁽ t ), Mb, ⁽ t ) )

= ma_s ⁽ t ) л Mb, ⁽ t )

I" ^{+ 1}( x , y ) = I" ( x , y ) = M e ( t )                      (4)

Where superscript n is the number of iteration and t =2 is the target point in the selected data array, which is the most important task for getting significant desire result. We know metal artifact is mainly occurred in the high intensity gray level of the CT images, so we have to take appropriate decision about target point selection for super artifact reduction from CT images.

Let us consider a rectangular filtered image domain Q := [0, q1] x [0, q2] with boundary Г : =dQ and let a gray-scale filtered image I be represented by a real-valued mapping I e L ” ( q ) . A widely-used way to smooth I is by calculating the convolution

⁽ K . * I ^{)( x} ) ^: = J K . ^{( x} - y ) I ⁽ y "dy (5) n

Where K . denotes the two-dimensional Gaussian of width (standard deviation) σ>0:

K . ^{( x} ) ^: =

2пст .■

(

■ exp

V

Hl 1

2 . ²

Gaussian convolution mainly is used for smoothing an image and the standard deviation is the degree of smoothness in the image. If we consider large standard deviation then we need large kernel size for better result because large standard deviation provides higher degree of smoothness.

• III. Evaluation Criteria

We investigate the filter performance by applying two metrics Mean Square Error (MSE) [20] and Edge Preservation Factor (EPF) [20].The edge preservation ability of the filter is compared by Edge Preservation Factor and it is computed using (EPF):

EPF =   ^ (Д / ^-Д / ⁾⁽ Д / ^ -A I ^)

,/ ^ ( Л /-Ы )²( A I_d -А /_d )^{2        1} ’

Where Δ I and Δ I d are the high pass filtered versions of images I and I d , obtained with a 3x3 pixel standard approximation of the Laplacian operator. The larger value of EPF means more ability to preserve edges.

Mean Square Error (MSE):

z x :ⁱ z ;y i < x . y ) - I, ( x , y »2

MxN

Where the image size is M × N . x means row, y means column, I means original image and I d means filtered image.

• IV.    Experimental Result

  The proposed method has been applied to 2-D axial CT image with have been corrupted by metal artifact. The computation is carried out on MATLAB 7.12.0.635(R2011a) in a Core i5 2.50GHz and 4GB RAM laptop having a Windows 7 operating system. Here, we show the filtered images and try to depict the performance of filters about metal artifact reduction in Table 1-4 and Visual performance is also shown in figure 1-7 respectively.

Here, we represent our experimental result in subjective about artifact reduction in axial CT images. Filtered images are given below for making sense about filter performance:

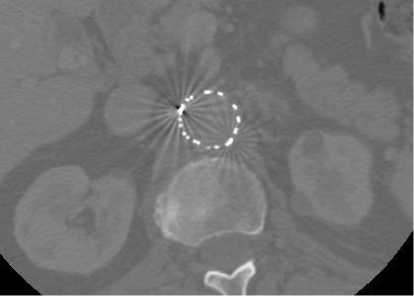
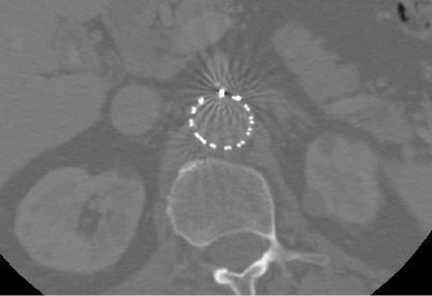
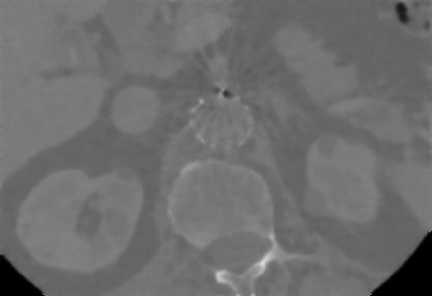
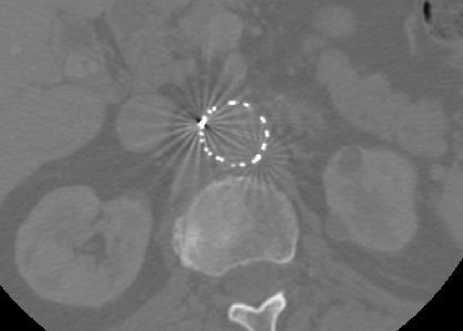
From figure 2 and 3, we see that filtered images are more stable and clear rather than previous metal artifacts affected images and the huge amount of artifact is reduced from the original images as well as the investigated filter creates the highly smoothing and better visual quality in the same time as well. So, we can say that filter is more powerful and efficient for artifact reduction for making stabilized filtered images.

(a)

(a)

(b)

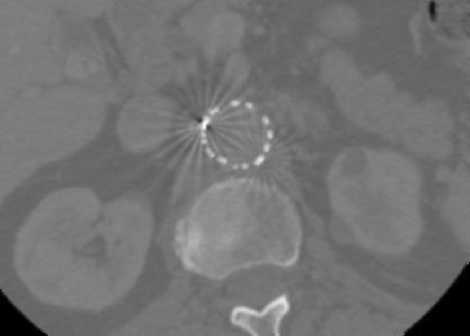
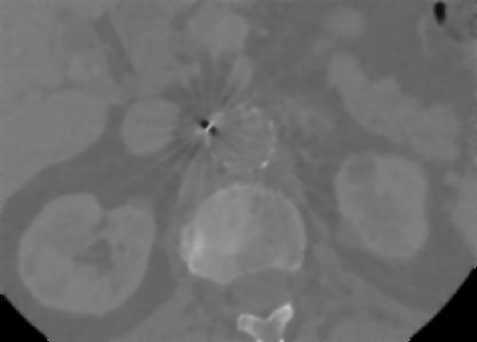
Fig. 3. 2-D axial CT image2 with artifacts present in fenestrated superior mesenteric stent, (a) before filtering image and (b) after filtering image

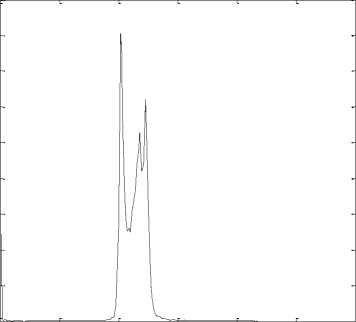
Graphical representation is the most important scientific parameter for judgments of the any types of imaging operation and the contrast measurement is another valuable approach for image quality judgment. If in the filtered images remain small amount of variation which reflects in the measurement curve then this filter suitability must be better for any kinds of imaging operations. Histogram of original images and filtered images are given below:

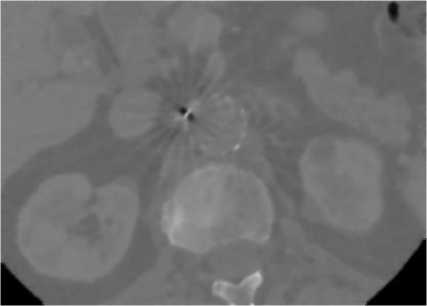
(b)

Fig. 2. 2-D axial CT image1 with artifacts present in fenestrated superior mesenteric stent, (a) before filtering image and (b) after filtering image

Original image

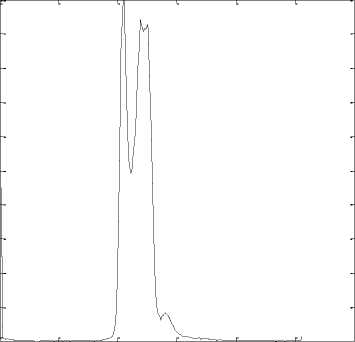
0      50      100     150     200     250     300

(a)

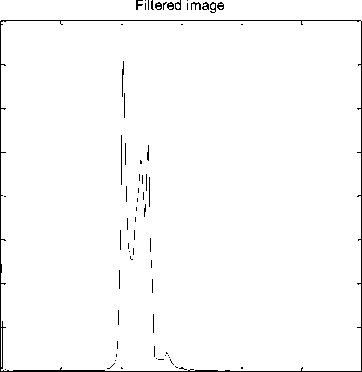
0      50      100     150     200     250     300

(b)

From figure 4 and 5, we see that filtered images are maintained structural view and enhance the contrast of the artifact corrupted images by reducing metal artifact from the axial CT images.

Statistical comparisons among some state-of-the-art algorithms are given below:

Table 1. Statistical performance of filters for 10 iterations

Methods	axial CT image1		axial CT image2
	EPF	MSE	EPF	MSE
Perona-Malik	0.9767	33.1962	0.9777	32.7307
SRAD	0.9658	39.5125	0.9665	38.5421
LPND	0.8841	62.3937	0.8892	62.3974
EER	0.9738	6.4990	0.9793	6.4801
Proposed	0.9796	0.0757	0.9828	0.0747

Fig. 4. 2-D axial CT image1, (a) Original image histogram and (b) Filtered image histogram

Original image

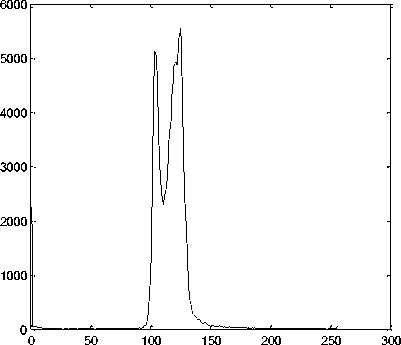
Table 2. Statistical performance of filters for 30 iterations

Methods	Stent wire image1		Stent wire image2
	EPF	MSE	EPF	MSE
Perona-Malik	0.9383	93.0890	0.9580	92.4121
SRAD	0.9257	41.1252	0.9274	41.2351
LPND	0.8830	62.5916	0.8885	62.6194
EER	0.9761	6.4981	0.9799	6.3806
Proposed	0.9796	0.0757	0.9828	0.0747

(a)

Filtered image

0       50      100      150     200     250      300

Table 3. Statistical performance of filters for 50 iterations

Methods	Stent wire image1		Stent wire image2
	EPF	MSE	EPF	MSE
Perona-Malik	0.8712	115.6091	0.9123	116.2183
SRAD	0.9058	43.9022	0.9064	44.6547
LPND	0.8822	62.7793	0.8878	62.8186
EER	0.9781	6.4901	0.9803	6.1302
Proposed	0.9796	0.0757	0.9828	0.0747

(b)

Fig. 5. 2-D axial CT image2, (a) Original image histogram and (b) Filtered image histogram

Table 4. Statistical performance of filters for 100 iterations

Methods	Stent wire image1		Stent wire image2
	EPF	MSE	EPF	MSE
Perona-Malik	0.8652	138.9465	0.8871	141.5765
SRAD	0.8740	45.7412	0.8714	47.9514
LPND	0.8798	63.1864	0.8858	63.2603
EER	0.9778	6.4851	0.9781	7.2805
Proposed	0.9796	0.0757	0.9828	0.0747

CT images than others existing well defined algorithms. The investigated method can reduce artifact significantly while edges, textures and point targets are smoothed as well as preserved without loss of any clinical information. Our filter alleviate artifact but do not make additional errors or noises in the filtered image which thing is mentionable with respect to others filter performance comparatively. In this experiment we did not use iteration for our filter but other filters are iterative.

Visual comparisons are given below with respect to our filter:

(b)

(c)

(d)

(f)

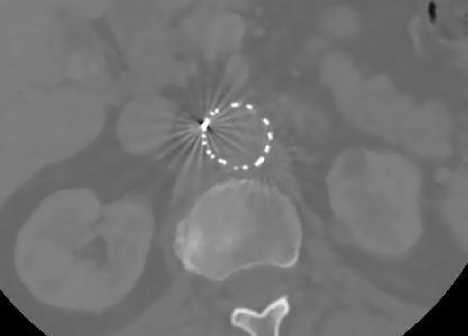
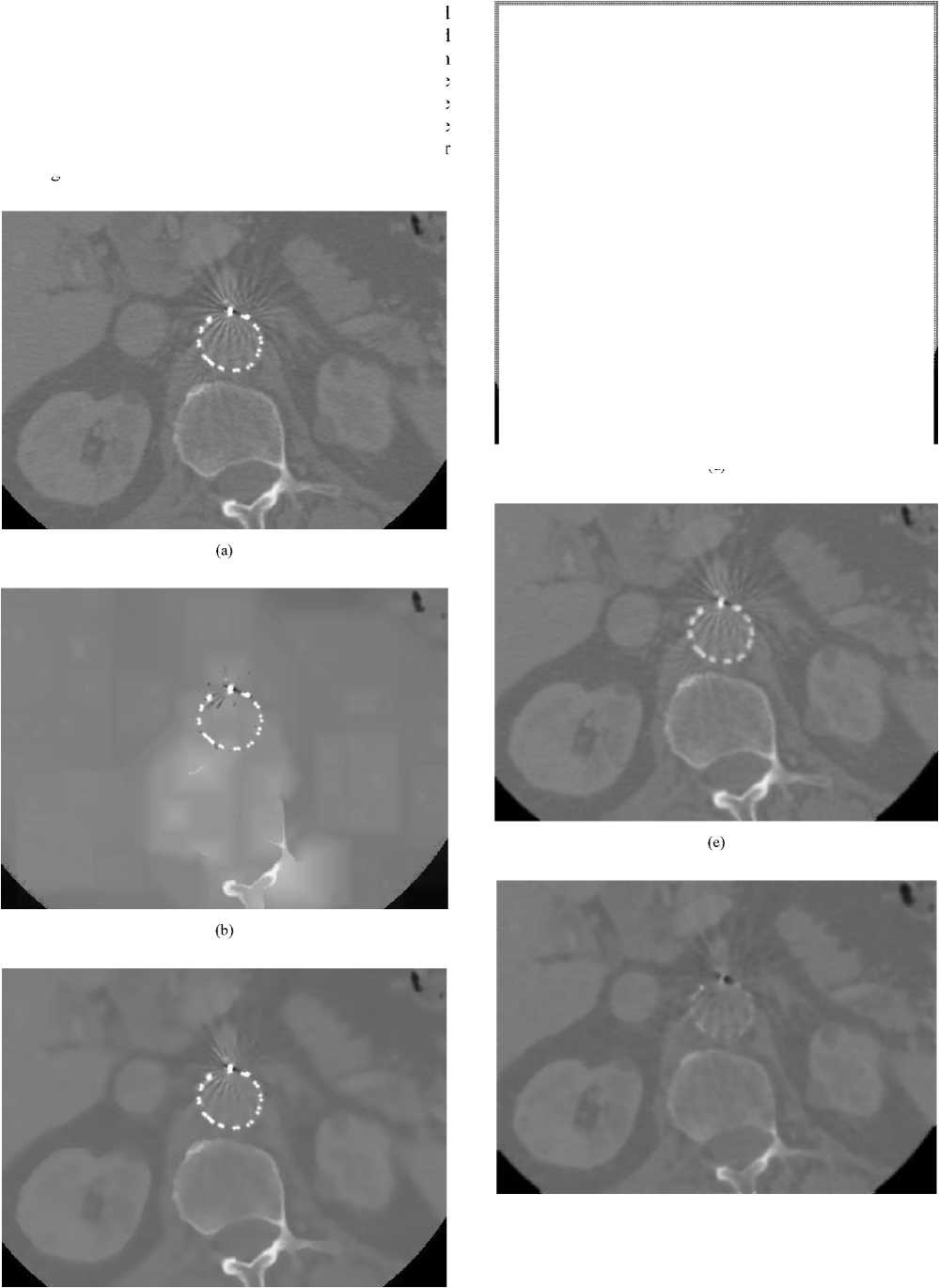
Fig. 6. (a) 2-D axial CT image1 with artifacts present in fenestrated superior mesenteric stent, (b) Perona-Malik (λ=4), (c) SRAD, (d) LPND, (e) EER, (f) Proposed method. The number of iterations is 50 in (b)-(e) except only (f).

(f)

(c)

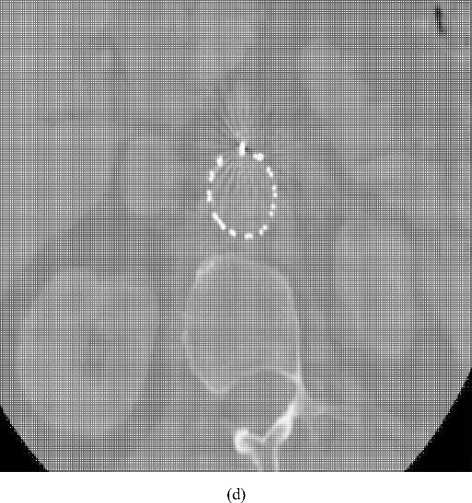
Fig. 7. (a) 2-D axial CT image2 with artifacts present in fenestrated superior mesenteric stent, (b) Perona-Malik (λ=4), (c) SRAD, (d) LPND, (e) EER, (f) Proposed method. The number of iterations is 100 in (b)-(e) except only (f).

From figure 6 and 7, we can see that our proposed filtered image is much clearer than other existing filtered images that mean noise reduction capability is very high of the proposed method in homogeneous and edge portions. Existing filters are unable to reduce excessive edge noises and in the mean time those filters blur the image and lose the clinical information only except our investigated method.

• V.    Conclusion

In this paper, we proposed direction oriented iterative reconstruction filter with fuzzy logic which is depends on automated intensity of CT image for metal artifact reduction. The Experimental results on CT images show that the proposed method can reduce artifact effectively and significantly while edges, textures and point targets are smoothed as well as preserved. Simulated artifact corrupted CT images show better visual quality. This method mainly depends on the signal direction according to the magnitude variation in the CT images. Our proposed method is especially effective for highly inhomogeneous image and can be used widely for artifact and the calcification plaque strongly reduction and the enhancement of the structure of artifact affected CT images.

Acknowledgement

We would like to thanks professor Dr. Zhonghua Sun for providing these images.