Method for optimization of information security systems behavior under conditions of influences

• І.    I NTRODUCTION

  The development of modern informative and communicative technologies influences on all spheres of human activity, rising their effectiveness, and simultaneously causing a set of uncontrolled threats, also including in informational sphere. Due to this, requirements for security of crucial important informational resources rise constantly. Today, key and crucial international laws in informational security (hereinafter referred to as “ISec”) management sphere and information security are series of standards ISO 27k. According to them, the main procedures for organization an effective system of ISec management are resources management, communication and operation management, risks management, work persistence management, ISec incidents management etc. Incidents management, according to international standard ISO/IEC 27035:2011, allows to reveal, analyze and investigate effectively, and in proper time, ISec incidents for minimization negative consequences for informational systems (hereinafter

referred to as “IS”) and organizations in general. Besides mentioned international standard, today there are many trade laws, and also practical recommendations and guides, that are based on the best world incidentmanagement practices. According to these documents, carrying out a procedure of incidents management is entrusted to specialized groups of fast reaction, which according to their functional peculiarities, provide for their clients certain services. Among basic services, should be mentioned identification and incidents analysis, reaction to incidents and their investigation, IS threats analysis, and also examining their endurance by simulation of attacks and impacts. Taking into consideration that success of realization of informational impact on the system, depends on its vulnerabilities, and in worse case turns into an incident, the investigation of system behavior under the influence of informational impacts, from the point of information security, is actual area for scientific research.

• II.    Related Works

Let’s review modern approaches to modeling of impacts on IS, we will mention input and output data of every criterion, main operations and also their advantages and drawbacks [1-3,5,8] (Table 1). The carried out research of modern methods of impacts simulation on informational systems has provided a possibility to define the most effective approaches (they are marked using grey color in the table 1) and to use them in order to optimize parameters of security systems. Taking into consideration the carried out research, today many tasks have left, and the task of solving them, have scientific and practical value. From this point of view, the designing and research of optimization methods of security systems indicators under conditions of influences are actual scientific task. Taking into consideration this point, the purpose of this work is security systems behavior under conditions of designing a method of optimization of information informational influences.

Table 1. Analysis of methods of impacts modeling on IS

No.	Name	Input data	Output data	Main operations (mathematical tool)	Advantages	Drawbacks
1.	The Mukchin-Volokita model [8]	Statistical data selection	Calculation of threats impacts on information	Expert estimations, graph theory	High accuracy of impact detection	A need of statistical data, dependence on competence of experts
2.	The Bell–LaPadula model and Biba model [8]	Sets of objects and subjects, and also their states, requests	A level of integrity breach	Sets theory, Boolean algebra	Simplicity of realization, integrity control	Taking into account only integrity; a possibility of creating of two-way information flow, and as a result is necessary to create trustful flows
3.	The Hartson model (five-dimensional model) [6]	Resources and their states; users and their responsibilities	A sphere of system security	A Cartesian product	A possibility of obtaining quantitative values	Abstract formalization of attack process
4.	A model on base of neuron Markov chains [3]	Statistical data for learning neuron networks, and specifying matrixes of probabilities conversions of Information Security System (ISS)	Identifying viruses, spam and attacks on Web-services	A theory of neuron networks; Markov’s chains theory	Adaptive identifications of attack and information security	A need for statistical data set for dynamical functioning
5.	A model on base of Petri-Markov networks [1]	Informational states of system (more then 3)	A possibility of realization of threats impact on information	Petri network theory and Markov chains theory	Quantitative estimation with taking into consideration time parameters	Difficulties of calculations for practical realization
6.	Differential gaming one-criterion column model [3]	The set of IS states	Optimal strategy of information security	A column theory, differentialgaming simulation	It allows to carry out distribution of informational resources, that are assigned to informational security	It doesn’t show general dynamics of influence on information
7.	Differential-gaming spectral one-criterion models [3]	The set of IS states	Optimal strategy and price of the game (guaranteed level of security)	Differentialgaming simulation	Low calculating difficulty, taking into account non-stationary processes	Not accurate step-by-step process of influence on information
8.	Differential-gaming Teylor model [3]	Flow intensity of protective and attacking actions	Trajectory and price of the game	Differential conversions of Teylor type	Accurate description of attack on information	High calculating difficulty, low level of scientific-technical researches
9.	Hybrid differentialgaming model [3]	Reliability and security indicators, threats probability, time parameters	Optimal distribution of security resources	Differentialgaming simulation	Taking into account an indicator of ISS qualitative functioning; high accuracy even in uncertain cases	Accuracy is reached only with using certain mathematical methods (consecutively)
10.	Constant discrete differential-gaming model [3]	Ultimate set of system state	Optimal security resources distribution in real time	Numeral-analytical simulation, differential conversions	Extension of simulation range of impact on information, low calculating difficulty	It doesn’t take into consideration all criteria (comparing with multicriteria models)
11.	Multi-criteria differential-gaming model on base of integral optimality [3]	Strategies of opposing parties, time parameters	Optimal players strategies, price of the game (guaranteed security level)	Differentialgaming simulation, a theory of decision making	A possibility of information security under condition of conflict of partial criteria, and unauthorized distribution of informational resources of attacking party	Limitations on partial criteria of quality
12.	Multi-criteria differential-gaming model on base of non-linear scheme of compromises [2,3]	Intensity of resources distribution flow of opposing parties, time characteristics	Optimal strategies of opposing parties	Differential conversions, a theory of support of decision making	Realization simplicity, adaptability to different situations	Notable drawbacks haven’t been found

• III.    Theoretical Basis of Optimization Methods of Security Systems Indicators under Conditions of Influences

A typical task of ISS behavior research under conditions of influences on information, is optimal resources distribution of player of security in correspondence with player of influence. Let suppose two systems. One of the system is system of influence (SI) is a player, that influences on information of another system (Information security system, hereinafter referred to as “ISS”), a player, that ensures security.

To carry out this task, SI uses certain amount of methods and influential means. The influential means of SI consist of S types, and they are in certain conventional units, quantity of means of m -th type is equal to a . The total attacking potential of SI M is a

S 1

value, that is equal to M_x = ^ a_m .

m = 1

The information that should be protected, has n informational blocks         , besides the value of -th i,..., n                                                       i block is evaluated by certain conditional value v, where i = 1,...,n . Let mention that the informational blocks B.,...,Bn, are sorted by their value, i.e. v > • • • > v.

Let suppose that every unprotected informational block B during influence on information and realization of single influence using means of m -th type, loses its characteristics – integrity, availability and confidence. The value of losses from influence on information in ISS on B. -th informational block is evaluated by value v s_m .

The total losses of integrity, availability and confidence of information I ( 2 , ц) , which define its security in ISS, only if availability of influences and opposition can be evaluated by value, proportional to difference of their total quantity, if it is positively defined, and equal to zero in opposite case, i.e.

I ( 2 , ц )

n                  S 1

^ v i max к £ e_m

I = 1                m = 1

(

^ im к

^ ² mj ² ij j = 1         )

where ц is an intensity of flow of informational influences, that are assigned by SI to influence on B -th informational block using means of influence of m -th type;

2 is an intensity of flow of actions, that are assigned by ISS for ensuring security of B -th informational block using means of ensuring security of j -th type;

2 is an intensity of flow of actions, that are assigned by ISS for preventing influence from means of m -th type, using means of ensuring security of j -th type.

The distribution of means of ensuring security of j -th type, that are assigned by ISS for preventing influence

S 1 from means of m -th type on condition that ^ 2_mj = 1, m = 1

• 1    <  j <  S^ and 1 <  m <  S_x , can be showed in matrix view:

^л=IM               (2)

using correspondence limitations

0 <  2 mj <  2 m max                 (3)

where 2 max is maximum intensity of flow of actions, considering ensuring security 2 ._max = 1.

Let the total value of losses of information in ISS I(2, ц) (1) be the main characteristic of informational conflict, and its source is opposition of interests of ISS and SI. However, ISS tries to improve the information security by reducing the value of total losses (1), that are caused by actions of SI’s influences. The goal of SI is the opposite, that’s why the function (1) can be accepted as a fee of information security ensuring system for SI. As a result, the task of synthesis of optimal behavior in the system “security-influence” comes to antagonistic game of two players with convex function by one variable 2 and function of win I(2, ц) (1), when the second variable ц has arbitrary fixed value.

Proceeding from a methodology of finding the solutions of antagonistic games for convex function by one variable of function of win [2,4,7], let’s form a task of synthesis of optimal behavior in “security-influence” system in view of the following a theorem.

• A.    Theorem 1

Let a fee I ( 2 , ц ) be persistent function of win with two variables 2 and ц for antagonistic game, which is strictly convex by 2 for each arbitrary fixed ц , and has on single range first derivative by 2 . Then only one optimal protective strategy exists for ISS Z op , that is stepped function of fee I(2^pt , ц ), and 2^pt = const , and the only answer of equation is

I(2^opt , ц ) = max I(2^opt , ц )           (4)

0 < ц < 1

If two players – SI and ISS have chosen the optimal strategies д ^opt and 2^opt , then the price of the game I * can be defined as

I * = min max I ( 2^opt , ц^opt )            (5)

0 < 2 < 10 < ц < 1 ^{x           7}

• B.    Proof

Optimal strategy of player of influence дopt can be defined depending on value of optimal strategy of player who ensures security Xop . If the player, who ensures security, chooses one of the optimal strategy:

[1,

X°Pp = ^      , 8X     X(6)

, ^{1 ( л}"' • ^"' ⁾ > 0,

I then player of influence will choose the following strategy popP = const, that will satisfy the conditions

0 < popP < 1(7)

and expression (5).

If the player who ensures security evades sticking to the optimal strategy X^opP in range 0 <  X < 1 , then the player of influence will choose the strategy like

p ( a ) = aI ( X, p₁ ) + ( 1 - a ) / ( X, p₂ )          (8)

where a , p , p are arbitrary constants, that meet the conditions

Taking into consideration the equation (10), SI chooses mixed optimal strategy p ( a ) , that is certain convex combination of finite quantity of pure strategies.

Let’s bring in some designations. Let X i = | ^p i i ,-,P iS ₁ ||, Y = || ^X i 1 -- A s 2||, ^z = | V^ 1 - • У ^s ₁ ||. Then the fee (10) with considering accepted designations can be showed in matrix view:

n

I ( X , p ) = S max { 0, Z ' ( X i -Л Y, )}       (11)

i = 1

where Z ' is transposed matrix to matrix Z ■

Due to the reason, that function of fee I ( X , p ) (1) is convex by X for every arbitrary fixed p , then SI during forming the optimal strategy p ^opP can use randomized strategy only among those pure strategies, that are the tops of simplex:

popP

S 1

'I S 4

0 <  a <  1 , 0 <  p ₁ <  1, 0 <  p ₂ <  1

ILv',P1 )=ILv',P2)= I, d1    ’P1)>0, dX

^{8 1} (^⁾ <  0, a ⁸ I (F ^ + ( 1 - a ) ⁸ ’   ■ P 2 ⁾ = 0

ЭX              ЭX     v '    ЭX

S where 5; > 0 , S 8i = 1 ■ i=1

And the fee (1) with considering (12) acquires the following view

(          ^

S 1

I ( X , p ) = IX , S ^a i. < S 5 i I ( X , a^

v    i = ¹      7

i = 1

C. Note

Used requirements in function of fee I(X, p) (1) can be weakened.

First, it is possible to neglect the conditions of existing the derivatives. But in this case, is supposed the existing of single sided derivative functions I(X, p) at every point of interval of its defining. Then the conditions, that are put on the derivatives

dIX, P1) and 8I(XopP, P2 ) 8X           8X are

interchanged by corresponding conditions for single sided derivatives at the indicated points.

Second, the condition of strict convex of function of win I(X, p) is possible to weaken, by interchanging it by condition, that it is convex. But it leads to situation, that optimal strategies as for the first popP, and as for the second XopP player, are not the only.

On base of theorem 1 and taking into consideration the note, the optimal strategy for ensuring security of ISS XopP can defined from equation inf sup I(X, p) = sup I(XopP, p) = I       (10)

X p           p

Let’s mark by Im a part of price of the game I* , which can be obtained by SI on account of using the means of influence of m -th type, that

S 1

S I m = I * m = 1

and

Q = p,■■■,aSi  . Then, for defining the strategy of ensuring security of B -th informational block for ISS, according to stated theorem no. 1, we obtain the matrix equation

Q -л Y = I i             (14)

To solve this matrix equation (14) is worth using generalized inverse matrix of Moore–Penrose, first time implemented in work [9].

Let for rectangular matrix Л [9] exist generalized inverse matrix of Moore-Penrose Л + , for which the following conditions are true [9]:

ЛЛ + Л = Л , Л + ЛЛ + = Л +

( лл⁺ ) * = ЛЛ + , ( л⁺л ) * = Л + Л         (15)

where Л * is the conjugate transposed matrix, which for matrix Л in range of real numbers is transposed, i.e.

*

Л = Л ' .

Thus, for non-particular square matrix Л (2) is defined generalized inversed matrix Л⁺ , which matches with ordinary inversed matrix Л ^-1, i.e. Л⁺ = Л ¹ = || ^ ||.

Taking into consideration the peculiarities of generalized inversed matrix (13) from matrix equation (14) we receive

^d 1        ^dS 1

V ^{( 1 )} ”"’ w ( ⁵ 2 )

, W = I ¹

^ 1

^IS 1

^s s 1

proceeding from accepted designations, let’s go over from the equation (20) to its matrix form

Л⁺ W = 5 ( л ⁺ Q - R )             (21)

Y i =Л⁺ ( Q - Ji)              (16)

After using the peculiarities of generalized inverse matrix (15) from the expression (21) after simplification, we have

where the strategy of ensuring security of B -th informational block by means of ensuring security of j -th type of ISS ^ , that defines the intensity of actions flow considering ensuring security, with taking into account accepted above designations, acquires the view

W = Л 5 ( л ⁺ Q - R )             (22)

where the part of price of the game I , that is the fee of ISS for losses of the most valuable information, is defined as

[

^ ij = Z в jm I a m

I m  I

V^ m J

I

m

S ₂

J

^m Z T j=1 LV( j )

S 1

W ^{( j} ) Z L a m

^- d j

Let’s presume, that ISS places its means of preventing of j -th type among the most valuable information w ( j ) , i.e.

4 ( J ) + 1, J = ^ ( j ) + 2, J = ... = ^ , j = 0        (18)

The SI will act optimally, if it influences on the most valuable information w = max w ( J ) , which the ISS ensures security with certain probability p . Besides the price of the game for SI can be defined as

Summarizing the values (17) by all n informational blocks B ,..., B and taking into account the presumption (18), we define the strategy for player in case of ensuring security for the most valuable information:

S ₁            S ₁   S ₂                       S ₁

I * =Z Im =ZZ ^m^m" V( J )Z Pjmam - dj m=1       m=1 j=1   V (j) _      m=1

D. A conclusion from the theorem 1

V (j)                51                        51

Z L W(J )Z Mm - Lv(j)Z L™( i=1            m =1                 m=1

V ^{( j} ) j ^{where L} v 0) ⁼ Z“ .

i = 1 ^V i

Mathematical expectation of win by all means of influence on every block of information B , for which is ensured security by all means of ensuring security by ISS, doesn’t depend on number of informational block i , i.e. PV = c = const . Taking into consideration the condition

V ^{( j} )

As Z ^j = dj , according to presumption, and taking i = 1

V of settings Z Pi = 1, we have pt = < i=1

у ,1 <  i <  v ; /v?

0, i >  v ,

where c =

into consideration (19), we have

S 1 Z P j-im = m = 1      b m	1 L V ( J )	Г v ( J )Z ' в jm a m _       m = 1		dJ J	(20)
	V ( 1 ) L v ( 1 )	0      ...	0
Let’s designate	... 0	V ( 2 ) ... L V ( 2 ) ...      ... 0      ...	0 ... W ( 5 2 ) L V ( 5 2 )	,

[:Z 7

V i = 1 ^V i

- 1

J

.

^L V

Thus, the synthesis of optimal behavior of ISS-SI, is defined by optimal strategies of the players in informational conflict, the expressions (6) and (12) correspondingly.

E. Example

Let the ISS choose arbitrary strategy for ensuring security, but it is not optimal (6), then the choice of optimal strategy (12) by SI, guarantees its win in fee E not less than the price of the game I ^* (24), i.e.

=

L v

S 1

v

E1 = I i=1

m

^V i^L V m = 1

S 1

I S m a

S 2 S 1

II P jm a m ^ mj j = 1 m = 1

S 2

S 1

S ₂

^: m ^— I ^A mj ^A ij j = 1

V ₁   S 1       S 2

— I T ISm I Aj i=1   V m=1     j =1

S1

E 2 = ViI Sm Ц —I Am m =1

S1                S2

< V i { I S m [ a m — II Mmj m = 1             j = 1 m = 1

P jm\ a m

—

Im

<

ViSm

^ISm I V( j)IPjmUmXmj m =1    j=1 _      m=1

S 1

—

L v ( j )

S ₁        S ₂

I S m I j- m = 1     j = 1 L V ^{( j} )

S 1                 S 2    S 1

< V i { I S m [ a m — II P jm a m A mj + m = 1             j = 1 m = 1

S ₁   S ₂

= II; ' m v ( j ) I M.

m = 1 j = 1    V ^{( j} ) _       m = 1

m

—

d j

= I *

= vi

S 1

Es a mm m=1

^-

S 1                  S 1

^m mm m = 1            m = 1 v i

> = I (26)

Let suppose that the strategy of influence of SI is not optimal, then proceeding from the matrix equation (11), the losses of information in ISS don’t exceed the values

Proceeding from these ratios, is followed the truth of stated according to the theorem no. 1 expressions. Thus, the theorem n 1 has been proved.

^E 2 ^:

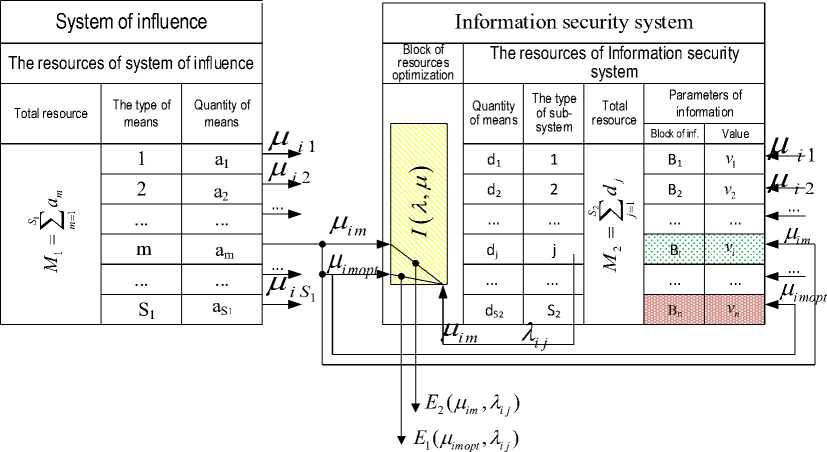
Fig.1. A scheme of representing the method of optimization of information security systems behavior under conditions of influences

The suggested method of optimization of information security systems behavior under conditions of influences is represented in fig. 1. A typical task of research of behavior of security system under the conditions of influences is optimal resources distribution of player of security, corresponding resources of player of influence.

• IV. Experimental Research of Method of Optimization of Security System Indicators under Conditions of Influences

• A. Estimation of predicted and current level of informational resources security for different strategies of forming system security

The task of synthesis of optimal behavior with using developed software, allows to evaluate the predicted I (Apt, ^pp) current I (A, ^) levels of informational resource security, depending on strategies A and ц , that are chosen by players – the subjects of conflict on defined interval [t0, T], where t0 a moment of time at the beginning of informational conflict, T the time of its ending. The procedure of evaluating comes to simulation of antagonistic game of two players.

In this work is researched three strategies of forming system security [3, 12, 13]: a strategy of forming of echelon security system with n barriers of security, a strategy of withdrawal of player of influence to erroneous informational resource with further involving it in informational conflict, and a strategy of estimation of security level using a pattern of normal system behavior.

According to description of method of optimization of security system behavior under conditions of influences, the security level, depending on chosen strategies of forming such systems, in general view is defined according to (1). Besides, for different strategies of security system security, that are chosen by player of security, the predicted I (A o^¹ , ц ^орр ) and current I ( A , ц )

levels of security of informational resource, acquire the values, that vary in range i _G [ 0,1 ) . Let’s evaluate the predicted and current level of informational resources security for each of them.

The strategy of forming of echelon security system with n barriers of security is described in works [3, 5, 15]. In fig. 2 is described a graph model of attacking process (impact) on echelon security system.

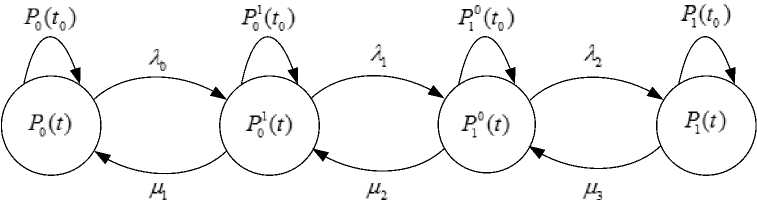
Fig.2. A graph model of attacking process (impact) on echelon security system

In fig. 2 P ( t ) is a probability of stay of security system under the influence of unauthorized access (hereinafter referred to as “UA”), P ₀¹ ( t ) is a probability of stay of security system under the influence of UA means during action of securitize methods, P ₁⁰ ( t ) is a probability of stay of security system under the influence of security during action methods of UA, P ₁( t ) is a probability of stay of security system under the influence of security methods, A , A , A , д , д , д are intensities of flow of securitize actions and informational attacks under corresponding probabilities. P ( t ) , P ₀¹( t ₀) , P ₁⁰ ( t ₀ ), P ( t ) are starting conditions for corresponding probabilities.

For this strategy in work [3, 13] was shown, that during using of echelon security system with 4 barriers of security (n = 4) and arbitrary strategies of security and influence, the expression of evaluation (1) acquires the view:

I ( A ), ^a i , ^д ) ua = 1 - “A)T ⁺7 ^ 0 ( A )^{+ д ) t 2} - 26

• - ~ ^{A ( a} 0 ^{+ 2 A} 0 ^д 1 ^{+ A} 1 ^д 1 ^{+ д 2} ) T 3 .

On base of shown expression and step of change of A parameters (the intensity of securitize actions per unit of time), д (the intensity of influences per unit of time) and time t , and using software «Optima – 2014 v.1.0», we have received the following dependences of security level (table 2).

Table 2. The security level of security system during using the echelon security system

λ	μ	T=0,2 sec	T=0,4 sec	T=0,6 sec	T=0,8 sec	T=1 sec
0,00	1,00	1,000	1,000	1,000	1,000	1,000
0,25	0,00	0,975	0,952	0,929	0,906	0,885
0,25	0,25	0,976	0,953	0,932	0,912	0,893
0,25	0,50	0,976	0,955	0,935	0,917	0,900
0,25	0,75	0,977	0,956	0,938	0,921	0,906
0,25	1,00	0,977	0,957	0,940	0,925	0,911
0,50	0,00	0,952	0,906	0,864	0,824	0,786
0,50	0,25	0,952	0,909	0,870	0,834	0,801
0,50	0,50	0,953	0,912	0,876	0,843	0,813
0,50	0,75	0,954	0,915	0,880	0,850	0,822
0,50	1,00	0,955	0,917	0,885	0,856	0,828
0,75	0,00	0,929	0,864	0,805	0,751	0,701
0,75	0,25	0,930	0,868	0,813	0,764	0,719
0,75	0,50	0,931	0,872	0,821	0,775	0,732
0,75	0,75	0,932	0,876	0,827	0,784	0,742
0,75	1,00	0,933	0,879	0,833	0,791	0,748
1,00	0,00	0,906	0,824	0,751	0,685	0,625
1,00	0,25	0,908	0,829	0,761	0,700	0,643
1,00	0,50	0,909	0,834	0,770	0,712	0,656
1,00	0,75	0,911	0,839	0,777	0,721	0,664
1,00	1,00	0,912	0,843	0,784	0,728	0,667

In fig. 3 is shown the dependence of security level I ( Я , ц) on time t .

As it is seen from the table 2 and fig. 3, if the players have chosen the optimal strategies of security and influence correspondingly, the predicted level of informational resource security using the echelon security system will be equal to 0,667 (for T = 1sec ), i.e. I(Я^рР , Ц ^оР ) = 0.667. For the rest of occurrences, when the players evade from optimal strategies, this value varies in range of specified limitations.

In fig. 4 P0 (t) is a probability of stay of security system under the influence of UA, P01 (t) is a probability of stay of security system under the influence of UA when security methods are active, P10(t) is a probability of stay of security system under the influence of security methods when methods of UA are active, P1 (t) is a probability of stay of security system under the influence of security methods, Я, Я, Я, Ц, Ц, Ц are the intensities of flows of security actions and informational attacks for corresponding probabilities.

For this strategy in work [3, 5, 14] was shown, that in case of arbitrary security strategies and influence the expression of evaluation (1) acquires the view:

I ^{( я} 1 , ^Я 2 , ^ц 1 , ^ц 2 ) UA

= ¹ - ~ ^{( Я} 1 + ^Я 2 ) T +

- ((я1 + Я2 )2 + Я1Ц + Яц2 У2 - ~ (( (Я1 + Я Х(Я1 + Я )2 + 6                          24

^{+ Яц} 1 + Я ^ц 2 ^{+ Яц} 1 ^{( 2} Я ^{+ Я + Ц} 1 ^{) + Я} 2 ^ 2 ^{( 2 Я} 1 ^{+ Я} 2 ⁺ ^ 2 ) .

On base of this expression and step of change of Я parameters (the intensity of security actions per unit of time), ц (the intensity of influences per unit of time) and time t , and using software «Optima – 2014 v.1.0», we have received the following dependences of security level (table 3).

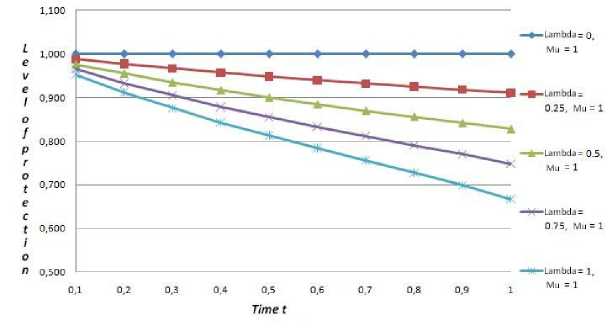
Fig.3. The dependence of security level I ( Я , ц ) on time t in case of using the echelon security system

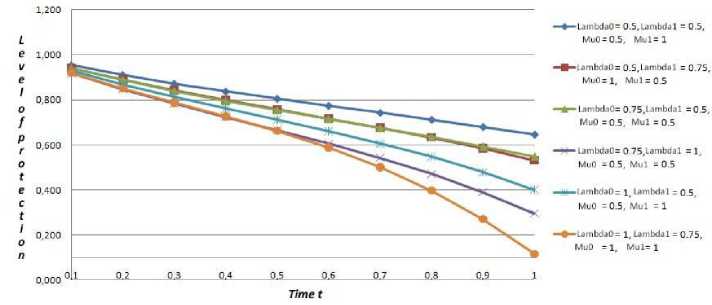
Fig.4. The dependence of security level I ( Я , ц ) on time t in case of using the strategy of withdrawal of player of influence to erroneous informational resource with further involving it in informational conflict

As it is seen from the table 3 and fig. 4, if the players have chosen the optimal strategies of security and influence correspondingly, the predicted level of informational resource security using the strategy of withdrawal of player of influence to erroneous informational resource with further involving it in informational conflict, will be equal to 0,6044 (for T = 1sec ), i.e. I(ЯрР,^pp) ® 0.6044 . For the rest of occurrences, when the players evade from optimal strategies, this value varies in range of specified limitations.

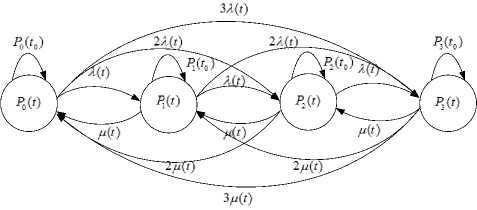
Fig.5. A graph model of process of attack on security system, that uses the strategy of estimation of security level using a pattern of normal system behavior

The strategy of estimation of security level using a pattern of normal system behavior is described in works [3, 5, 10, 16]. In fig. 5 is shown a graph model of process of influence (attack) on security system, that uses the strategy of estimation of security level using a pattern of normal system behavior.

In fig. 5 P ( t ) is a probability of system failure under the influence of attack, P ( t ) is a probability of stay of system under the influence of attack when information security methods are active, P ( t ) is a probability of stay of server under the influence of information security methods when attack is active, P ( t ) is a probability of stay of server under the influence of information security methods, ^ ( t ) , ^ ( t ) are the intensities of flows of protective actions and informational attacks, that are chosen by players of conflict.

Table 3. The security level of security system during using strategy of withdrawal of player of influence to erroneous informational resource with further involving it in informational conflict

λ 1	λ 2	μ 1	μ 2	T=0,6 sec	T=0,8 sec	T=1 sec
0,00	0,00	1,00	1,00	1,000	1,000	1,000
0,50	0,50	0,50	0,50	0,768	0,707	0,646
0,50	0,50	0,50	1,00	0,774	0,712	0,646
0,50	0,50	1,00	0,50	0,774	0,712	0,646
0,50	0,50	1,00	1,00	0,780	0,717	0,646
0,50	0,75	0,50	0,50	0,715	0,636	0,549
0,50	0,75	0,50	1,00	0,720	0,633	0,529
0,50	0,75	1,00	0,50	0,717	0,633	0,532
0,50	0,75	1,00	1,00	0,722	0,630	0,512
0,50	1,00	0,50	0,50	0,663	0,560	0,438
0,50	1,00	0,50	1,00	0,662	0,541	0,380
0,50	1,00	1,00	0,50	0,661	0,547	0,401
0,50	1,00	1,00	1,00	0,660	0,528	0,344
0,75	0,50	0,50	0,50	0,715	0,636	0,549
0,75	0,50	0,50	1,00	0,717	0,633	0,532
0,75	0,50	1,00	0,50	0,720	0,633	0,529
0,75	0,50	1,00	1,00	0,722	0,630	0,512
0,75	0,75	0,50	0,50	0,662	0,558	0,434
0,75	0,75	0,50	1,00	0,660	0,541	0,385
0,75	0,75	1,00	0,50	0,660	0,541	0,385
0,75	0,75	1,00	1,00	0,659	0,524	0,336
0,75	1,00	0,50	0,50	0,606	0,472	0,296
0,75	1,00	0,50	1,00	0,597	0,432	0,197
0,75	1,00	1,00	0,50	0,598	0,438	0,215
0,75	1,00	1,00	1,00	0,589	0,398	0,116
1,00	0,50	0,50	0,50	0,663	0,560	0,438
1,00	0,50	0,50	1,00	0,661	0,547	0,401
1,00	0,50	1,00	0,50	0,662	0,541	0,380
1,00	0,50	1,00	1,00	0,660	0,528	0,344
1,00	0,75	0,50	0,50	0,606	0,472	0,296
1,00	0,75	0,50	1,00	0,598	0,438	0,215
1,00	0,75	1,00	0,50	0,597	0,432	0,197
1,00	0,75	1,00	1,00	0,589	0,398	0,116
1,00	1,00	0,50	0,50	0,547	0,371	0,125
1,00	1,00	0,50	1,00	0,528	0,307	0
1,00	1,00	1,00	0,50	0,528	0,307	0
1,00	1,00	1,00	1,00	0,508	0,243	0

For this strategy in work [4, 9] was shown, that that in case of arbitrary security strategies and influence the expression of evaluation (1) acquires the view:

I * A M ) U = 1 - A T 2 + ^ A ) (18- A + M T 4 —

• - 4- A [ 3A ( 18 A ) + 7 M ) ) + ' M ) ( 77 A ) + 53^ 0 )V 6 84 у 4 )

On base of this expression and step of change of A parameters (the intensity of protective actions per unit of time), m (the intensity of influences per unit of time) and time t , and using software «Optima – 2014 v.1.0», we have received the following dependences of security level (table 4).

As it is seen from the table 4 and fig. 7, if the players have chosen the optimal strategies of security and influence correspondingly, the predicted level of informational resource security using the strategy of estimation of security level using a pattern of normal system behavior, will be equal to ),6)44 (for T = 1sec ), i.e. I( A p , M op ) ~ )-215 . For the rest of occurrences, when the players evade from optimal strategies, this value varies in range of specified limitations.

Table 4. The security level of security system during using strategy of estimation of security level using a pattern of normal system behavior

λ	μ	T=0,2 sec	T=0,4 sec	T=0,6 sec	T=0,8 sec	T=1 sec
0,00	1,00	1,000	1,000	1,000	1,000	1,000
0,25	0,00	0,990	0,961	0,917	0,860	0,796
0,25	0,25	0,990	0,962	0,919	0,867	0,808
0,25	0,50	0,990	0,962	0,921	0,872	0,815
0,25	0,75	0,990	0,963	0,923	0,876	0,817
0,25	1,00	0,990	0,963	0,925	0,878	0,814
0,50	0,00	0,980	0,925	0,845	0,751	0,645
0,50	0,25	0,980	0,926	0,849	0,760	0,654
0,50	0,50	0,980	0,927	0,853	0,766	0,653
0,50	0,75	0,981	0,928	0,856	0,770	0,642
0,50	1,00	0,981	0,929	0,859	0,771	0,621
0,75	0,00	0,971	0,892	0,783	0,656	0,485
0,75	0,25	0,971	0,893	0,788	0,664	0,476
0,75	0,50	0,971	0,895	0,792	0,667	0,452
0,75	0,75	0,971	0,896	0,796	0,666	0,413
0,75	1,00	0,971	0,897	0,799	0,662	0,360
1,00	0,00	0,961	0,860	0,727	0,560	0,257
1,00	0,25	0,962	0,862	0,732	0,562	0,215
1,00	0,50	0,962	0,864	0,736	0,559	0,153
1,00	0,75	0,962	0,865	0,740	0,550	0,072
1,00	1,00	0,962	0,867	0,742	0,537	0

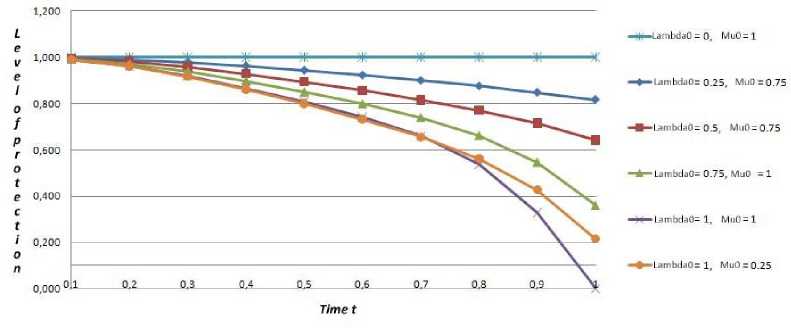
Fig.6. The dependence of security level I ( A , m ) on ti^me t in case of using the strategy of estimation of security level using a pattern of normal system behavior

Therefore, with help of software «Optima – 2014 v.1.0», has been evaluated the predicted and current level of informational resources security for three strategies of forming the security systems: the strategy of forming of echelon security system, the strategy of withdrawal of player of influence to erroneous informational resource with further involving it in informational conflict and the strategy of estimation of security level using a pattern of normal system behavior. In this work has been defined the predicted level of security of informational resource for each of examined strategies of forming the security system. As it is seen from results, the player of security can predict the security level and can optimize its resources, including those cases, when the player of influence uses optimal strategy.

In fig. 6 is shown the dependence of security level I(X, ц) on time t .

actions.

On base of plurality of identifications LI and set of linguistic links LC the plurality of rules has been formed for revealing vulnerabilities

ER ⁼ 1 U ER i 1

n

B . Simulation of current is states for checking a possibility of identification a vulnerability of informational systems in under the conditions of influences

where ER i ( i = 1, n ) - is a sub- plurality of possible rules for revealing i -th anomalous state, caused by i -th attack (influence), besides

For evaluating the vulnerabilities of IS the following parameters have been chosen: the intensity of actions ( I actions ), the capacity of used RAM ( V RAM ), CPU load ( P CPU ), the time of process preforming ( T proc ), the quantity of executable processes ( K ExProc ), the type of executable files of influence ( F type ), the quantity of failures and errors ( K faliures ), unusual processes ( K UnsualProc ).

In process of attack (influence), the violator, influences on the system, changes its certain parameters, creates or stops processes that are peculiar to it etc. All these actions are reflected on the state of the system. Evaluating these parameters is possible to reveal the fact of influence and to identify the vulnerability of IS under conditions of influences [4,9]. So far the process of revelation and identification of vulnerability happens in case of uncertainty, and above mentioned parameters have not clear character, then the functioning of this system has to be based on non-precise logic. For identification the violator is possible to use logic-linguistic approach and base model of parameters, partly described in [2, 10, 12], which have been the base of developed software.

With help of developed software, using experimental approach has been developed a model of standards of linguistic variables for non-precise parameters of violator identification among chosen plurality of parameters using a work [5, 13, 16, 18].

Using an experimental approach, the rules have been formed, that they are aimed at vulnerabilities identification under conditions of influences. These rules

n             n     r n

U ER . = U b ER j \ i = 1             i = 1 [ j = 1

= { ER_n,ER 12 ,...,ER 1 r } ,

where ER j ( i = 1, n , j = 1, r n ) - is a j -th rule of i -th sub- plurality of possible rules, and a r i ( i = 1, n ) a general number of possible rules, intended for revealing of i -th anomaly. According to the work [3, 11, 15] is followed

n

ri

ER=UU ER»j • i=1 I j=1

ⁿ         ri ,

=и Ю (

n      r i

U | U ERi, i = 1 I j = 1

n

ri

i = 1 I j = 1

= ( LCir,

LC irj ^

^l*A =

^ LI ir>

j

allow to reveal anomalous state of IS, caused by violator activity, on base of using the methods of non-precise logic, expert estimations and models of standards of parameters, that are necessary for revealing the violator. Forming the rules has been carried out with help of corresponding model [3,13], and for creating it, the plurality of linguistic identifications has been brought in

where ER_ir is r_j -th rule of revealing anomaly, caused by i -th, that word for word is interpreted as: “If LC_ir is true, then the level of anomalous state, that can be caused by i -th attack, will be LI_ir ”.

The developed software «Optima – 2014 v.1.0» allows to evaluate the predicted and current security level of informational resources for such strategies as the strategy of forming of echelon security system with n barriers of security; the strategy of withdrawal of player of influence to erroneous informational resource with further involving it in informational conflict; the strategy of estimation of security level using a pattern of normal system behavior. The received results have confirmed trustworthiness of developed method of optimization of information security systems behavior under conditions of influences.

d

is quantity of

plurality elements, that are necessary for representation of anomalous state, and LI i ( i = 1, d ) elements of LI, each of them assumes one of the test values, that characterize in linguistic form the level of anomalous state of the system, that can be caused by attacking

V. Conclusions

Thus, in this article has been developed a method of optimization of information security systems behavior, that due to taking into account the parameters of security system (the quantity of security means, type of security sub-system, total security resource and value of

information), allows to define optimal behavior in system “influence-security”. In addition, specialized software has been developed, that allows to verify the suggested method. The received results can be used for expansion of tools of groups of fast reaction to ISec incidents, ISec units of organization, and also for rising effectiveness of developing methods and information security systems.

Acknowledgement

This scientific work was supported by RAMECS and CCNU16A02015.