Method of selecting technologies of a manufacturing enterprise to carry out projects on their improvement on the basis of the theory of fuzzy sets

One of the crucial tasks of carrying out a policy of technical and technological improvement at a manufacturing enterprise is searching for advanced technologies, necessary to focus the engineers' attention on, to improve them.

Most often this problem is solved by means of analysing the previous operational background of the enterprise. We investigate one of the criterion K_i :

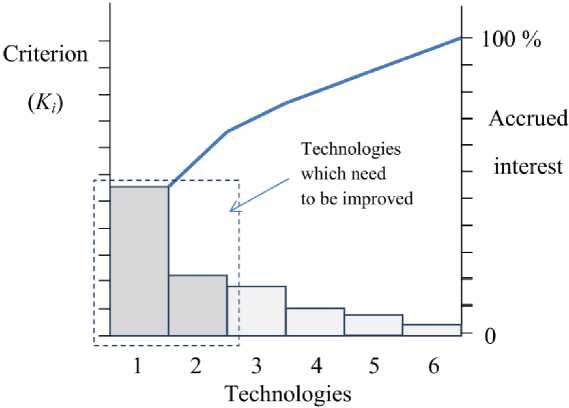
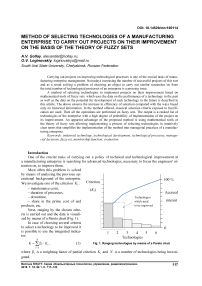
Fig. 1. Ranging technologies by means of a Pareto chart

– maintenance costs,

– duration of processes,

– downtime,

– share in the prime cost of end products, etc.

Next, ranging by the chosen criteria is carried out and the data is visualized by means of a Pareto chart (Fig. 1).

In case of choosing several criteria to select a technology to be improved it is possible to use the integrated indicator:

N

K = ∑ β i ⋅ K i ,                (1)

i = 1

where β _i is a weighting factor of partial criterion K_i and N is a number of technologies being investigated.

Краткие сообщения

Applicability

After defining a concern within the technology used, the project [3] on its improvement is initiated. Such projects can often fail in the end as researchers fail to receive a solution giving significant improvements. Therefore the task to increase the efficiency of the choice made to build a portfolio of projects of the enterprise in the area of technological improvements and increasing a share of successful projects is relevant.

Time

Fig. 2. Logistic (S-shaped) curve of development of technologies: I – onset phase, II – rapid growth phase, III – a maturity phase

Development of technologies curve

It is known that any technical system including technological processes follows the law of development in a logistic curve [10]. At the moment of its occurrence (Fig. 2, phase I), the technology possesses low characteristics. Further, when it begins to gain greater popularity, a large number of researchers contribute to its essential development (Fig. 2, phase II). When approaching the limits of physics principles on which the technology is based, the potential for possible improvements becomes extremely limited (Fig. 2, phase III). In the saturation phase, even large investments in improving this technology don't lead to a dramatic growth of its characteristics. Failures of projects of technological development at manufacturing enterprises which are guided only by past performance of the enterprise may account for this phenomenon.

Thus, the knowledge on regularity of development of technologies has to be used when building a portfolio of projects on improvement.

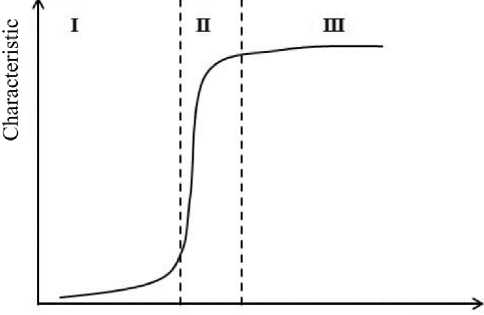
Let's consider a set of technologies which are available at the enterprise (Ω), (Fig. 3). As a result of selection based on historical record, it is possible to reveal a subset of “problem” technologies A ( A ⊂ Ω ) on set Ω. As stated above, subset A contains technologies having both essential and not essential potential for development (Fig. 3, a). For carrying out an analysis of available technologies from the point of view of the potential for improvement, we shall select subset B (B ⊂ Ω ) as a set of technologies having a high potential for improvement. Interception ( A ∩ B ) will represent a set of technologies having both an essential value for the enterprise and a high potential for improvement (Fig. 3, b). The efficiency of the projects aimed at improving technologies from subset ( A ∩ B ) will be higher.

a)                                                 b)

Fig. 3. Venn diagrams for the array of technologies of the enterprise: a) selection on the basis of historical data, b) selection on the basis of historical data and accounting the curve of development

Method of selecting technologies for their subsequent improvementon the basis of the theory of fuzzy sets

The task of selecting under investigation contains a considerable uncertainty owing to a set of factors influencing the performance of the enterprise. It is appropriate to express the information using fuzzy sets. The founder of the mathematical theory of fuzzy sets is L.A. Zadeh [15]. A significant contribution to its development was made by A.N. Borisov [1, 2], S.A. Orlovsky [9], H. Raif [12],

A. Coffman [5, 6], etc. Among the modern writers there are A. Piegat [11], S. Gotvald [4], A. Nedose-kin [8], V. Siler [14], A. Shatalov [13], D. Mukhamediyeva [7].

The most expedient algorithm to select the technologies for implementing projects on their improvement is as follows (Fig. 4).

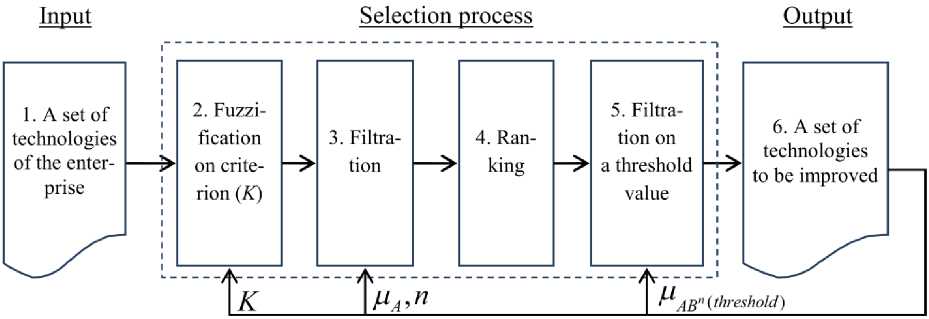
Fig. 4. Flowchart of selecting technologies for implementing projects on their improvement

Box 1 (Input). A set of technologies of the enterprise. Each manufacturing enterprise can be presented as a set of technologies whose identification and formalization is an important part of a managerial process. On the output of the process of selecting technologies, the whole set of technologies to select is given.

Box 2. Fuzzification on criterion ( K ). The importance of each technology being investigated can be estimated by the aggregated criterion K (1). Then it is necessary to carry out the procedure of fuzzification (interpreting it in the terms of fuzzy sets). For this purpose we shall define fuzzy set A by means of membership function ц A : А ^ [0,1]. Membership function ц A takes on values from 0 to 1 and shows a membership degree of element a g a to fuzzy set A . Usual set A is called a basic set.

Let basic set A be a set of technologies of the enterprise which need to be improved:

A = { «technology- 1 »,« technology 2 »,. . ,« technology N » } .                                         (2)

Then the fuzzy set of the technologies which need to be improved will be set as follows:

.4 = { («technology 1 », ц _a 1 ), («technology 2 », ц _a 2 ), . , («technology N », Ц a_N ) } ,                       (3)

where цa is a function of membership of i-technology to fuzzy set A, a1 is technology 1, a2 is tech- nology 2, etc.

If we choose such test of ranking ( K ) that the greater its value, the more the enterprise needs improvement of this technology, to describe the membership function we can choose the S -shaped function which is described by the following equations:

f 0,             a <51, s (a, 51,52,5g) = <

a ^-5 1 I (5 з —5 1 ) ,

1 - 2

a ^-5 3 (5 3 -5 1

5 1 <  a < 5 2 ,

5 2 <  a < 5 ₃ ,

1,

a >5 3 ,

where 5 2 =

5 1 +5 ₃

Generalizing the opinion of experts answering the following question: “At what value of criterion ( K ) does the technology needs to be improved first of all?”, it is possible to calculate the values and to construct the membership function (Fig. 5).

Краткие сообщения

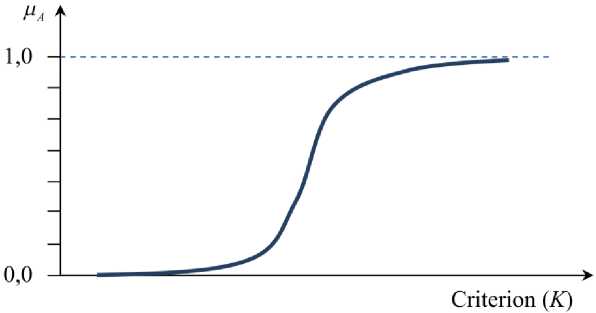
Fig. 5 The membership function showing the membership of technology to the set of “technologies which need to be improved” depending on the design criterion

Thus, at the output of this block there will be fuzzy set A in which membership function ц _a will be prescribed for each technology of the enterprise (3).

Box 3. Filtration. Let's address to Fig. 2 where it was shown that development of technologies occurs along an S-shaped curve. Phase II i.e. development (rapid growth) is of the greatest interest for implementing projects on improvement. Developing technologies in phase I is too risky and is inclined to high probability of failure. Development of technologies in phase III doesn't seem promising as the limits of physical laws are reached. In phase III it is necessary to conduct researches in order to replace a technology with a radically new one.

Let's address to the experts with a question whether the technologies belong to a phase of rapid development (in terms of the theory of fuzzy sets).

Let's introduce fuzzy set B as a set of technologies being in the stage of rapid development:

B = { («technology 1 », ц b ), («technology 2 », ц b 2 ), _ , (« technology N », ц b N ) } ,                      (5)

where ц b is a function of membership of i -technology to fuzzy set B i .

Next, to realize the filtration let's introduce an operation on the fuzzy sets of the following form:

ц AB =ц a(a) -ц B(b), ц 2 =ц A(a) -цВ(b),

AB                                                                                              (6)

ц AB " =ц A ⁽ a ) ^- ц В ^{( b ).}

In essence this operation represents using a filter once, twice and n times. The multiplicity of filter ( n ) depends on how important the researcher considers a factor of development of technology along an S -shaped curve of development.

At n = 0, цAB0 = цA (a) ■ ЦB (b) = ц A (a) ■1 = ц A (a),                                                            (7)

i.e. the filter isn't applied and ranking is made only taking criterion K into account.

Box 4. Ranking. Let's carry out ranking (ordering) of technologies according to decreasing membership function. The greater value, the more important (more “problem”) the technology for the enterprise and more promising (from the point of view of realization of potential for development) the technology is.

Box 5. Filtration on a threshold value. It is possible to introduce threshold value u n„. The tech-AB nologies having a membership function less than this value will be considered unpromising for implementation of projects on their improvement (Fig. 6).

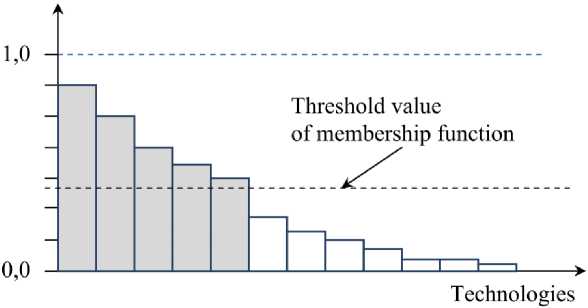
Fig. 6. Realization of ranking and filtration on threshold value of membership function µ n

AB

Box 6 (Output). A set of technologies to be improved. Following the end of a selection process, at the output we shall have a ranked list of technologies of the enterprise which can be used to build a portfolio of projects on improving the operational activity.

Adaptation of the method

While implementing the projects the adaptation of the offered method can be required. Here are the following parameters which can be changed in it:

– criterion K (partial criteria K_i ) – box 1,

• –    a function of membership of i -technology to a fuzzy set of technologies which need to be improved µ _A (Fig. 5) – box 3,

• –    multiplicity of filter n – box 3,

• –    threshold value of membership function µ _{n ( threshold )} – box 5.

Conclusions

The offered method of selecting technologies of the industrial enterprise allows increasing a share of successfully implemented projects on improvement of operation activities due to the selection using both the data on past periods of the performance of the enterprise and the knowledge of the stage of development of the technology. A definite advantage of the offered method is using mathematical tools of the theory of fuzzy sets allowing the process of selection of technologies in intuitively clear terms that simplifies implementing the method in the managerial practice of a manufacturing enterprise.