Methodological principles for the formation of a number of unified space communication satellite platforms

Developing rocket and space products is always carried out using the process stock of technical solutions and technologies, which means repeatability is an integral property of a new product. At the same time, its effectiveness and competitiveness depend on the product novelty. Therefore, developing space technology requires to find a compromise between the repeatability and variability (novelty) of their properties, that is to determine the appropriate level of development continuity [1].

The main methodological principles of the development continuity is the unification of products and their components, technological equipment and technological processes, which allows to reduce their diversity and range. Ordering the products range and their components is achieved by developing parametric and standard series with rationally chosen intervals between adjacent members of the series according to a complex criterion that links the indicator of the target efficiency of the product with the cost of its development. These methodological principles are actively implemented when spacecraft (SC) of information support is developed [2; 3].

Design model of the SC target efficiency

In the parametric analysis of the possibility to locate a new payload on a unified space platform (USP), the principle of maximum satisfaction of the payload resource needs (mass, power consumption) of the spacecraft is implemented in the form of a generalized payload mass М ПН.об [1– 7]:

M ПН.об = M ПН + K W ’ ^W nН = M ПН ’ ^а пн , ^а ПН = ¹ + K W , ПН ,

M _ПН

^M ПН.об                  ^M ПН

KПН = , .    = аМ аПН ,  аМ = ,,  ,

MКА              MКА where MПН и WПН – mass and power consumption of the payload; αПН – coefficient of partial cost of resources to meet the needs of the payload; KW – average coefficient of partial costs of the SC mass to generate electricity and discharging heat, kg/W; KПН – specific generalized coefficient of partial costs of SC resources to solve the target problem; МКА – SC mass; αм – cost coefficient of SC mass per payload.

In this occasion, the generalized payload mass М пн.об can be used as an indicator of the SC target efficiency [1; 3; 4].

In the first approximation, the costs to perform SC research and development are considered proportional to the costs of SC manufacturing (C изг ) due to the design methods [1]:

C ОКР = K ОКР ’ C изг .                                      (2)

The K ОКР coefficient value is determined by the novelty of the developed SC and its components, the performance of SC ground experimental method and its components (payload, space platform). The SC manufacturing cost, as total costs to manufacture its components and their integration into the spacecraft, depends on its target efficiency, reliability, mass, power consumption and others. Taking into account the fact that SC mass М КА is limited by the energy capabilities of the launch vehicle and it is completely used to achieve the target tasks with a given efficiency and reliability; in design research it is applied as an equivalent of the SC manufacturing cost [1; 3; 4]:

C изг   C уд.и ' M КА .

The value of the specific indicator C уд.и is determined based on processing the statistical data on SC analogues.

As a result, we obtain a functional dependence of the cost inputs to conduct SC research and development on its mass:

C ОКР = ^K ОКР ’ C уд.и ’ M КА .

The resulting system of equations makes it possible to form a single-criterion objective function of the Э КА scalar type, defined as the ratio of the target efficiency indicator (М ПН.об ) to the indicator of financial costs to develop spacecraft (С ОКР ) [4; 8]

Э КА =

M ПН об C ОКР

M ПН об

^K ОКР ’ C уд.и ’ M КА

In the case of developing a new spacecraft based on the USP of the base spacecraft (the index "б" refers to the base spacecraft, and the index "н" to the new one), we introduce a relative (dimensionless) criterion (assuming С уд.и the same values) [4]

н    н   бб

ЭКА  M ПН.обM КА KОКР н   б    б    нн

Э КА   M ПН.об M КА K ОКР

н

K об 1           м     н    н

, ^{Й Э}н = _н ■ _н - ¹ , K об - K нб ' K Э ;

KНБ KЭ кЭ =

н

KОКР б KОКР

.

With the help of the generated criterion, we evaluate the range of effective application of the modified USP for a new spacecraft for various options of constructive implementation [9; 10].

Methodology to assess the range of USP effective application

When designing a new spacecraft based on the USP, here is a necessity to refine it to meet the needs of the new ПН in resources (in terms of mass and power consumption).

To determine the resource budget of the new spacecraft in comparison with the base spacecraft, we use the following equations [3; 4]:

M КА = M УКП + M ПН + ^K 0 ’ 5 M УКП ;                       (7)

$ M УКП = ^а м ( M ПН ^- M ПН ) + ^Kw ( W nH ^- W nH ) ,

Where M ^б – base platform weight, M ^н and W ^б – mass and power consumption of the payload of the new spacecraft; K_o - modernization depth factor, K ₀ = 0 г 1.

After appropriate transformations, we obtain the following expression to determine the new SC mass нн

M На = K н - M бд, 5 M_H = —ПН - 1,   8 W_H = W H - 1,               (8)

КА   нб КА     н _M б          н _W б

K Нб = 1 + « М ( 1 + K о '« М ) 8 — _H + K о '« М ( « Пн - 1 ) 8 - н .

We are carrying out similar transformations to determine the relative indicator of the generalized resource costs

K 6 = — H = 4- [ 1 + 8 — н + ( « Пн - 1) ( 1 + 8 - н ) ] = 1 + 4- [8 — н + ( « Пн - 1) 8 - н ] • ^— ПН.об « пн                                « пн

Introducing the resulting dependencies to K ^н и K ^н to the inequation (6), we obtain

^{8 —} н ^{[ 1   K} Э ^-« м ’«пн ( 1 ^{+ K} о « м ) ] ^—« пн ( ^K Э   1 )   ^{8 W} h ( « пн 1 )( 1   ^K 0 ■ ^K Э ^- « М ’^а пн ) .

Using the proposed SC design model and the selected single-criteria objective function δЭ , we evaluate the ranges of effective application of the basic USP for two options to implement the payload.

Option 1: the needs of ПН in resources are met by the USP in excess

^м M _ПН

м ^б к ^— пн

< 1,

^м W _ПН

W ПН

^

< 1 J

that

is the modifications of the USP are minimal (the creation of interfaces with the ПН), therefore, we assume

ИР                        ИР

K 0 = 0, 8 — ИР = 1 - -П^н = -8 — н , 8 W иp = 1 - - пн = - 5 W h •

M ПН               W ПН

Using the USP of a base spacecraft with an excess resource (UCP-ИР) for the ПН creates the prerequisites for the accelerated development of a SC with a new ПН, reduces the financial costs of its development ( K Ир <  1); however, it simultaneously reduces SC mission effectiveness Qsc ).

Taking into account the above information, equations (8)–(10) will take the following form:

KИР = 1 -«М-8—ИР      0<8—ИР < 1     0<8-ИР < 1;(11)

«пн 'Kоб; = «пн-8—ир-(«пн - 1)8-ир;(12)

(1 -KИР)«Пн -(«пн -1)8-ир —8—ир (1 -KИР -аМ Чн).(13)

We estimate the range of parameter changes 8—ИР и 8 —ИР, investigating inequality (13) due to the criterion K

« ^б _пн ( 1 - K ₃ИР )

• 1)    8 - ир = 0,     8 — ир <   -Р         = 8 — Иp .

  
  

¹ K Э ' « М ' « пн

«Lт-1

Assuming 8 — 0 <  1, we obtain K ИР —----^-н----r = K И, .

’                       « Пн ( 1 "« б, )

2) 8 — ир = 0,

^б - ^^ИР

8 - ир <--- i= 8 - Ир .

« пн ^{- 1}

Taking as 8 - °, < 1 , we obtain K И — -4 = K ИР .

« пн

Solving equations (13)–(15) together, we obtain a generalized expression for the range of parameter variation в ^ИР s вMИР

8 W p    ^в M И р.1

0 <8 W _OT< 1,  0 <8 M _ИР <  1.

K ИР <  ^а ПН   ⁸ M ^{ИР   ( а} П ^{н   1) 8} W P ,   — ИИР <  — ИИР <  К ИИИР <  1.            (16)

а Пн ( 1 -а М -8 M ир )           '       '

If we transform inequality (13) into equality (one-sided constraint) and introduce the resulting dependence 8 Wup от 8Mир

into the equation (12), we obtain formulae to assess the dependence of integral indicators only on 8Миp < 8M°p:

^— НБ = ^{1 а} М ’^{8 M} ИР ,     K ИР = ( 1 ^а М ^{-8 M} ИР ) K Эр = K НБ ’ K Эр ,

1 -а б < К ИР <  1,0 , 1 -а б < -об < 1,0.                       (17)

м    НБ              м      _и р

Option 2: to meet the increased requirements of ПН in resources, the improvement of the USP (USP-M) is needed, therefore, we believe — ₀ = 1.

Using USP-M for a launcher with an increased resource creates the prerequisites to increase the target efficiency of a spacecraft (Э ) with a new ПН, but simultaneously increases the financial costs for its development ( — Ир >  1).

In this occasion, the equations (8)–(10) are becoming:

мм

^M ПН             ^W ПН

⁸ M M “л ^б    ¹ ,      ⁸ W M = б ^{1 ;}

M ПН             W ПН

—Мб = 1 + аМ (1 + аМ)8MM + аМ (абПн -1)8Wm > 1;(18)

—Об = 1 + — [8Mm + (аПн -1)8Wm Ъ1;(19)

а

8Мм[1 - —М-аМ-аПн-(1 + аМ)]>аПн(—М -1)-8Wm (аПн -1)(1 - —М-аМ-аПн).(20)

Analysis of the resulting inequality (20) allows to formulate the following system of constraints:

1) 8 W m = 0,

M

'   ^{( — М -} 1)    , _=S<

МЧ Чн ( 1 + « М )    М

1+ Г а8

Assuming 8 М⁰_М <  1, we obtain — М <        ^Пн    = — М ;

^{1 + а} м ( 1 ^{+ а} м )

а П _н ( — ^М - 1 )

= 8 W M .

• 2)    ^{8 М}м = ⁰ ,    ⁸ W M =               м^^

( ^а Пн 1 )( 1   ^— Э ^-а М ’^а Пн )

2 а ?

Assuming Полагая 8 W ⁰ <  1, we obtain —^ <------у------у = —^ ,;

¹ + а М ( а П _н ^- 1 )      .

• 3)    assuming the positive value of the denominator in formula (21)

1 - — М - а б, - а б - (1 + а б,) >  0 , we obtain the constraint — М < —----= — М .

Э М ПН         М ,                                Э      _{б    б         б}        Э.3 .

^а м ^{- а} Пн ( 1 ^{+ а} м )

Solving equations (20)–(22) together, we obtain a generalized expression for the range of parameter variation

M г 1 - W , 0 <6 M м <  1, 0 <6 W м <  1,0,  1 < K Э < K М < K М < K М .

5 ^M м      ^{6 W} м

Introducing the obtained constraints into formulae (18), (19), we determine a two-sided constraint on the range of changes in integral indicators, taking into account their relationship, according to formula (6),

1 + « М ( « Пн — 1 ) 6 W^ <  K Нб <  1 + « М ( 1 + « М ) б MМ ;

1 +

«б^- ¹ 6 w 0 <  к м <  1 + ^{5 М}М б М     об        б

« ПН                « ПН

If we transform inequality (20) into equality (one-sided constraint) and introduce the resulting dependence 6WM от 6MM to equations (18) and (19), then we obtain formulae to estimate the de pendence of integral indicators only on 6MM мб к нб =1 + « М

« Пн ( K Э   1 ) ^{+ 6 M}M ’ « М

( 1   K Э • ^а М • ^а Пн )

> 1;

_м      ( к м - 1 ) +6 M m • к м •« М -« М

^об                      м б     б

( 1 ^к _э •« М - « ПН )

The obtained formulae to estimate the range of effective application of the modified USP for a new spacecraft are used to develop methodological principles to form a parametric series of basic spacecraft and basic USPs.

Methodological principles to form a parametric series of basic spacecraft (SC) and USP

Ordering the range of products and their components achieves due to developing parametric and standard series with rationally chosen intervals among adjacent members of the series according to a complex criterion linking the target efficiency indicator of the product with the cost of its creation [1; 11; 12].

A parametric series is a set of numerical values of the main parameter of a product. In the standard range, the main parameter is the geometric dimension. On the basis of these rows, a number of structurally similar (of the same type) product designs are created.

The process to determine the optimal composition and structure of the parametric series includes the sequential solution of three problems:

• –    determining the boundaries of the parametric series, highlighting the ranges of possible changes in the parameters of products;

• –    establishing regularities in the construction of series of the main and subordinate product parameters, assuming the identified boundaries;

• –    determining the optimal construction of a parametric series due to the criterion "efficiency -costs".

Developing a parametric series, as a rule, is based on the data of complex engineering forecasting of the development of products, methods and means of manufacture and deals with the main trends in their development identified in this occasion.

Assessing the possibilities while implementing a parametric series is carried out taking into account the sufficiency of technical and technological solutions, that results in forming a strategy to implement this series.

The boundaries of the parametric series are not stable and can change in both directions with the desired preservation of the regularities of the series construction.

Establishing regularities in the construction of a parametric series is performed on the basis of the choice of the nomenclature of the main parameters, which are weakly dependent on the design features and manufacturing technology of the product.

We are considering the application of these methodological principles to form a parametric series of SC information support (SCIS=КАИО) using the methodology to assess the range of effective application of USP. Based on USP, a number of structurally similar (of the same type) versions of the spacecraft are developed, therefore, the standard size range of the USP makes it possible to develop on their basis a continuous series of standard sizes of the spacecraft of various functional values, including the basic spacecraft for which these USPs have been developed. It is proposed to take the mass of the base spacecraft and the generalized mass of the payload as the main parameter of the SCIS parametric series.

The geometric model of the parametric series is shown in fig. 1, which demonstrates two basic spacecraft, the mass of which satisfies the condition

MМИР = MКИР -MКБМ >0.(27)

The basic SC with mass M ^БИР and the generalized payload mass M ^БИР is used to develop a new SC based on USP with an excess resource; the SC obtains the characteristics

ИР     БИР   ИР        ИР       БИРир

M КА = M КА ’ KНБ ,    Mпн.об = Mпн.об ' Kоб .(28)

The basic SC with mass M ^БМ and the generalized payload mass M ^БМ is used to develop a new SC based on USP with with insufficient resources; the SC obtains the characteristics

М    БМ  М        м      БМм

MКА = MКА ' KНБ ,     Mпн.об = Mпн.об ' Kоб .(29)

The value of the mass margin between the base spacecraft is derived from the following equation:

МИР

М    ИР    БМ  М    БИР  ИР          M КА M КА

Mu = MКА MКА = MКА ' KНБ  MКА ' KНБ ,  °Mu = , ,БМ л/БИР'100 %.(30)

^M КМ - ^M КАР

The condition M_u >  0 and 5 M_u >  0 provides the continuity of the series.

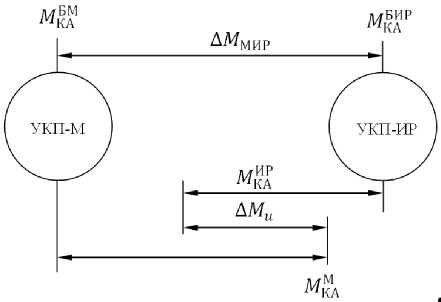
Рис. 1. Фрагмент параметрического ряда КА ИО с УКП: М – числовое значение главного параметра

Fig.1. Fragment of the parametric series of SCIS with USP:

M - numerical value of the main parameter

The margin for the generalized mass between the base spacecraft is derived from the equation:

M об = M М.об

—

ИР     БМ    М    БИР   ИР

M пн.об = M пн.об ' K об   M пн.об ' K пн.об ,

ш = MМ.об - MИоб об м™-мр™

■ 100 %.

пн.об      пн.об

The conditions M_{o б} > 0 and 5 M _oб > 0 provides the continuity of the series.

Therefore, using the information support as the main parameters of the SC parametric series (the mass of the base SC and the generalized mass of the payload of the base SC) permits to form a two-parameter criterion for the continuity of the series in terms of the margin of the main parameters between adjacent base SCs from the series.

We evaluate the effectiveness of the developed methodological principles to form a number of unified space platforms for communication satellites developed on the basis of the basic “Express-1000” and “Express-2000” USPs [13–15].

Estimated characteristics of the effectiveness range of the use of various basic USPs of geostationary communication satellites are given in Table 1.

When choosing the values of the relative cost indicator (K^ ) , the recommendation from [1] was used: Kм = 1,1, and Kир = 0,8. However, due to the constraints, these values have been refined in several cases.

Table 1

Efficiency range of USP application of geostationary communication satellites

Диапазон эффективности применения УКП геостационарных спутников связи

№ п/п		Луч-5А	Э-АТ2	Э-АТ1	Амос-5
1	USP type, row number	Э-1000А (1)	Э-1000К (2)	Э1000НТВ (3)	Э-1000Н (4)	Э-2000В (5)	Э-2000А (6)
2	M КА	1200	1350	1672	2100	2700	3550
3	M ПН	550	250	329	670	1193	1300
4	W ПН	1200	3000	5792	5880	10000	12100
5	M ПН об	670	490	712	1175	1775	2004
6	a м	0,458	0,185	0,197	0,319	0,442	0,366
7	а пн	1,22	1,96	2,16	1,76	1,490	1,541
8	K Эм	1,05	1,1	1,1	1,05	1,015	1,05
9	5 M М	0,422	0,37	0,49	0,396	0,619	0,403
10	м K нб	1,28	1,08	1,116	1,166	1,395	1,202
11	M КмА	1536	1460	1866	2450	3766	4266
12	м K об	1,346	1,19	1,227	1,225	1,415	1,262
13	M пмн об	902	582	874	1439	2512	2528
14	K Эир	0,80	0,80	0,80	0,85	0,85	0,80
15	5 M ир	0,44	0,55	0,653	0,504	0,510	0,562
16	K нибр	0,80	0,90	0,87	0,839	0,766	0,795
17	M КирА	957	1215	1459	1762	2094	2820
18	K оибр	0,64	0,72	0,70	0,714	0,656	0,635
19	M пинр об	428	352	497	838	1167	1273

The resulting array of information from the table 1 is used to build graphs to estimate the USP efficiency ranges and estimate the completeness of geostationary communication satellites with USP (Fig. 2, Table 2).

The resulting array of information from table 1 is used to build graphs to estimate the ranges of USP efficiency and estimate the completeness of geostationary communication satellites with USP (Fig. 2, Table 2).

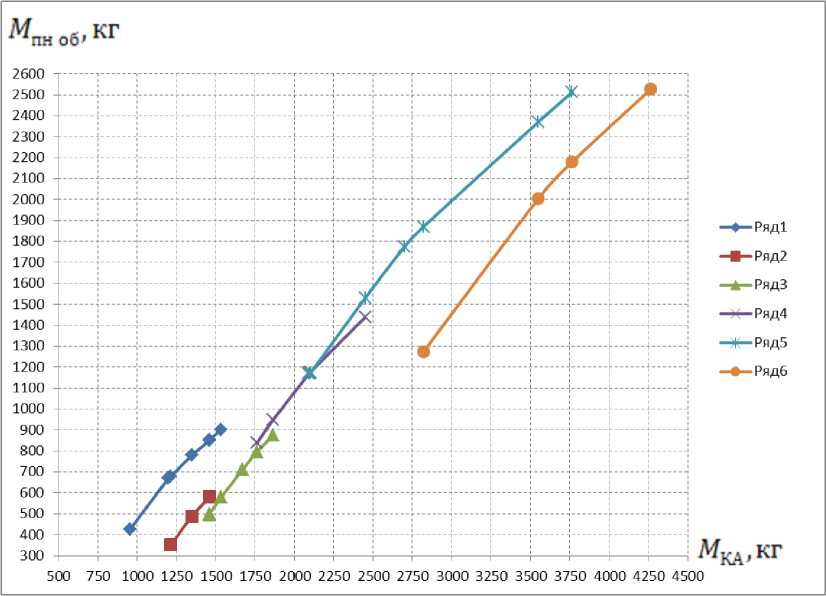
Рис. 2. Графики зависимости обобщенной массы ПН от массы КА для различных типоразмеров УКП и КА

Fig. 2. Curves of the generalized ПН payload mass dependencies on spacecraft mass for various USP sizes and SC

Table 2

Characteristics of geostationary communication satellites with USP

Характеристики ряда геостационарных спутников связи с УКП

№ п/п		Луч-5А	Э-АТ2	Э-АТ1	Амос-5
1	Type, data	Э-1000А (2011)	Э-1000К (2014)	Э1000НТВ (2014)	Э-1000Н (2011)	Э-2000В	Э-2000А
2	M КА	1200	1350	1672	2100	2700	3550
3	M ПН	550	250	329	670	1193	1300
4	W ПН	1200	3000	5792	5880	10000	12100
5	M ПН об	670	490	712	1175	1775	2004
6	K Эм	1,05	1,1	1,1	1,05	1,015	1,05
7	M КмА	1536	1460	1866	2450	3766	4266
8	M пмн об	902	582	874	1439	2512	2528
9	K Эир	0,80	0,80	0,80	0,85	0,85	0,80
10	M КирА	957	1215	1459	1762	2094	2820
11	ир пн об	428	352	497	838	1167	1273
12	M МИР		150	472	428	600	850

13	δ M u		214	16	24	59	111

The information analysis presented in table 2 reveals the following:

– it confirms the completeness of geostationary communication satellites developed by ISS “JSC”;

– the range of effective application of the “Э-1000K” USP is covered by the “Э-1000A” USP-M and “Э-1000НТВ” USP-ИР.

Conclusion

• 1.    The significant problem is formulated to formalize the methodological principles to find a compromise between the repeatability and variability (novelty) of the properties of new space technology samples - communication satellites.

• 2.    A design model has been developed and criteria for choosing the standard size of a universal space platform have been determined.

• 3.    Methodological principles for evaluating the effectiveness of the use of a universal space platform have been developed, that leads to estimate the resource requirements (in terms of mass and energy consumption) for a payload in a wide range of values.

• 4.    Methodical principles for the formation of a parametric series of basic spacecraft and USP have been developed using a two-parameter criterion to assess the completeness (continuity) of a series in terms of the margin in terms of the main parameters (spacecraft mass and generalized payload mass) between neighboring base spacecraft from a series.

• 5.    The developed methodological principles to form a number of unified space platforms made it possible to confirm the completeness of geostationary communication satellites developed by ISS “JSC”.