Метод блоков восстановления для повышения надежности программного обеспечения: сравнение с мультиверсионным программированием

DOI:

На сегодняшний день вычислительные машины являются распространенной частью нашего быта. Во многих сферах деятельности человека требуется высококачественное программное обеспечение (ПО) систем управления. Такое ПО может использоваться, например, в транспортной сфере, медицине, энергетической отрасли, финансовой и банковской сферах, космической и научно-исследовательской отраслях [1,2,3], причём список сфер, где применяются программные системы управления не ограничен лишь приведёнными выше пунктами. Однако существуют такие сферы человеческой жизнедеятельно, как, например, атомная энергетика или космические полёты, где надёжность ПО важна критически, поскольку полезный эффект от его работы за всё время использования может быть несоизмеримо мал по сравнению с негативными последствиями, ставшими результатом ошибки в этом программном обеспечении. Именно поэтому на сегодняшний день существует множество подходов и методов для повышения надёжности программного обеспечения, а само повышение надежности является актуальной задачей.

При безотказной работе аппаратной части причиной нарушения работы различного рода информационных систем могут служить конфликты между исходными данными и их обработчиком, то есть обработчик может некорректно обработать поступившие ему данные, особенно, если сами данные были некорректны [4]. Поэтому повышение надежности зачастую происходит путем усовершенствования программной части, хотя и валидности данных также уделяется большое внимание.

Любое программное решение должно обладать тремя ключевыми особенностями, для того чтобы считаться допустимым:

• •      Уметь диагностировать ошибку до того, как будет нанесен непоправимый

уровень повреждений.

• •     Уметь отбросить ложную информацию, возникшую впоследствии ошибки,

и вернуть систему в функционирующий режим работы.

• •      Уметь продолжить работу, ожидая, что последующая работа будет

выполнена [5].

Существует множество способов повышения надёжности программного обеспечения и его защиты от влияния ошибок, главным образом все эти механизмы используют тот или иной вид избыточности (временная, информационная или программная) [6]. Судя по количеству публикаций и активности авторов [7,8], на данный момент одним из популярных методов повышения надёжности ПО являются мультиверсионное программирование, основанное на программной избыточности [9].

Однако методу блоков восстановления уделяется, по мнению авторов, незаслуженно меньше внимания в научной литературе, хотя и его эффективность также остаётся достаточно высокой. Поэтому в данной работе рассматривается именно метод блоков восстановления для повышения надёжности ПО, а также сравниваются результаты его работы с классическим для мультиверсионного ПО алгоритмом голосования абсолютным большинством [10, 11].

ОПИСАНИЕ МЕТОДА БЛОКОВ ВОССТАНОВЛЕНИЯ

Метод блоков восстановления был предложен в 1974 году Джеймсом Хорнингом для возможности исправления ошибок и автоматизированного восстановления функциональности программы [12].

Суть метода блоков восстановления заключается в том, что для каждого программного компонента задаётся тест, проверяющий корректность его работы после каждого запуска. В случае возникновения ошибки или отказа одного из компонентов ПО, поочерёдно запускаются другие компоненты, функционально эквивалентные данному, то есть, каждый модуль содержит несколько версий, блоков, выполняющих одну функцию, но реализованных по-разному, каждый следующий блок запускается, если предыдущий не справился. Таким образом, отказ ПО с реализованным методом блоков восстановления возможен в случаях, если тест какого-либо блока даст сбой и пропустит ошибку или если закончатся блоки с алгоритмами.

Более наглядно упрощённая схема работы блоков восстановления представлена на рисунке 1.

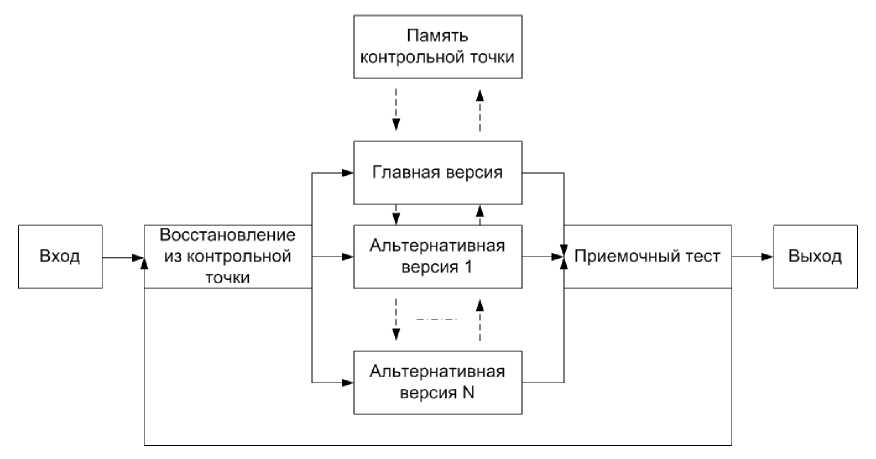
Рисунок 1. Модель блоков восстановления.

Figure 1. Recovery block model.

Как видно на схеме, данные подаются на вход, производится их запоминание на контрольной точке и последующая обработка на главной версии алгоритма, первым способом. Над итогом вычислений проводится тест и, в случае успешного прохождения теста передается на выход, но в случае, если тест не пройден, данные восстанавливаются на контрольной точке и проходят обработку на альтернативной версии алгоритма. Снова проводится тест и, по его результатам, данные либо подаются на выход, либо снова идут на контрольную точку.

МАТЕРИАЛЫ И МЕТОДЫ

Для проведения эксперимента, который смог бы показать эффективность подхода блоков восстановления, была создана база данных, состоящая из набора таблиц, код создания которых приведён в листинге 1.

Листинг 1. Структура базы данных для эксперимента.

CREATE TABLE module (

"id" integer primary key autoincrement not null,

"name" varchar(255) not null,

"round_to" integer not null, "min_out_val" real not null, "max_out_val" real null); CREATE TABLE version (

"id" integer primary key autoincrement not null, "name" varchar(255) not null, "reliability" real not null, "module" integer null, foreign key ("module") references module(id)) CREATE TABLE experiment_data (

"id" integer primary key autoincrement not null, version_id integer not null, version_name varchar(255), version_reliability real not null, version_answer real not null, correct_answer real not null, module_id integer not null, module_name varchar(255), module_iteration_num int not null, experiment_name varchar(31) not null, foreign key ("version_id") references version(id), foreign key ("module_id") references module(id));

Для проведения эксперимента были сгенерированы тестовые данные, которые имитировали работу двух мультиверсионных модулей, состоящих из 3 и 5 мультиверсий. Соотнесение версий с их априорными надёжностями (вероятностями безотказной работы) приведено ниже:

• 1.    V1 – 0.99;

• 2.    V2 – 0.98;

• 3.    V3 – 0.87;

• 4.    V4 – 0.999;

• 5.    V5 – 0.8.

В модуль, состоящий из 5 версий, входят все перечисленные выше версии, а в модуль, состоящий из 3 версий – только первые 3.

Поскольку тематика данной статьи не затрагивает вопрос получения корректных данных от мультиверсий, то и запрос, позволивший сгенерировать тестовые данные для этого эксперимента в статье, не приводится.

Для проверки гипотезы о не худшей эффективности блоков восстановления по сравнению с мультиверсионным подходом было проведено 2 эксперимента, в ходе которых были сгенерированы данные, выдаваемые описанными выше модулями. Эти данные имитируют реальную работу модулей, определяя, какой ответ будет выдан каждой мультиверсией, при этом определяется и верный ответ для каждой итерации. Каждый из модулей был запущен 1000 раз. В итоге для каждой итерации определялся верный ответ, который будет принят за ответ всего модуля, с помощью двух указанных выше подходов.

SQL-код, реализующий алгоритм голосования абсолютным большинством в контексте мультиверсионной парадигмы, и код, реализующий работу блоков восстановления, приведены в листингах 2 и 3, соответственно.

Листинг 2. Код алгоритма голосования абсолютным большинством.

• -- Голосование абсолютным большинством

select *, count(module_id) over() whole_answers_count, sum(is_correct_module_answer) over() whole_correct_answers, count(module_answers) over (PARTITION BY experiment_name) experiment_answers_count, sum(is_correct_module_answer) over (PARTITION BY experiment_name) experiment_correct_answers from (select distinct module_id, module_iteration_num, experiment_name, version_answer, correct_answer, version_answer_num, module_answers ,        case        when

CAST(max_version_answer_num as REAL) > CAST(module_answers as real) / cast(2 as real) then 1 else 0 end is_correct_module_answer from (select *, max(version_answer_num) over (partition by experiment_name, module_iteration_num) max_version_answer_num from (select id, version_id, version_reliability, version_answer, correct_answer, module_id, module_iteration_num, experiment_name, row_number() over (PARTITION BY experiment_name, module_iteration_num, version_answer) version_answer_num, count (version_answer) over (partition     by     experiment_name,     module_iteration_num)

module_answers from experiment_data where experiment_name in ('M3_I1000', 'M5_I1000')

) t

) tt where max_version_answer_num = version_answer_num ) ttt;

Листинг 2. Код алгоритма реализации подхода блоков восстановления.

• -- Блоки восстановления

select *, count(module_id) over() whole_answers_count, sum(is_correct_module_answer) over() whole_correct_answers

, count(version_answer) over (PARTITION BY experiment_name) experiment_answers_count, sum(is_correct_module_answer) over (PARTITION BY experiment_name) experiment_correct_answers from (select * , min(tt.version_id) over (PARTITION BY experiment_name, module_iteration_num) min_correct_version_id, abs(version_answer - correct_answer) < 0.00000001 is_correct_module_answer from (select *, t.version_reliability > t.test_pass_probability test_passed from (select id, version_name, version_id, round(cast(version_reliability * 1000 as INTEGER)) version_reliability, version_answer, correct_answer, module_id,        module_iteration_num,        experiment_name, round(cast(abs(random() % 1000) as INTEGER)) test_pass_probability from experiment_data where experiment_name in ('M3_I1000', 'M5_I1000')

) t

) tt where tt.test_passed = 1

) ttt where ttt.version_id = min_correct_version_id;

Стоит отметить, что в коде, реализующем работу блоков восстановления, для имитации прохождения версией проверки после её исполнения используется априорное значение надёжности версии – генерируется случайное число, значение которого сравнивается со значением надёжности версии, если оно не превышает значения надёжности, то тест считается пройденным, иначе, выход мультиверсии помечается как ошибочный вне зависимости от того, выдала версия правильный ответ или нет.

В качестве СУБД для проведения эксперимента была выбрана SQLite по причине своей легковесности, возможности быстрого развёртывания и переносимости.

РЕЗУЛЬТАТЫ

В результате проведённого выше эксперимента были получены данные, которые отражают количество успешно определённых верных ответов из общего количества обработанных групп ответов (итераций запуска мультиверсий).

Алгоритм голосования абсолютным большинством в эксперименте из 1000 итераций модуля, состоящего из 3 мультиверсий, определил корректно верное решение в 999 случаях, а для модуля, состоящего из 5 версий на выборке той же размерности – в 997 случаях. Итого, из 2000 обработанных итераций алгоритм голосования абсолютным большинством верно определил правильный ответ в 1996 случаях.

Подход повышения надёжности, использующий блоки восстановления показал себя следующим образом: в 996 случаях из 1000 при обработки данных модуля, состоящего из 3 версий, были выданы корректные результаты, а при обработке выборки аналогичного объема, представляющей собой результаты работы модуля, состоящего из 5 мультиверсий, корректно правильный ответ был определён в 997 случаях. Общим итогом работы данного алгоритма можно считать верное определение правильного ответа в 1993 случаях из 2000.

ОБСУЖДЕНИЕ

Из проведённого эксперимента видно, что результат работы алгоритма блоков восстановления сопоставим с результатом алгоритма голосования абсолютным большинством. При этом результат прохождения версией теста определялся случайным образом, а не реальным тестом, что также вероятно снизило показатель количества верных выходов модуля при использовании блоков восстановления.

Также стоит отметить, что при использовании мультиверсионного подхода версии зачастую выполняются параллельно, что может служить причиной взаимного влияния их друг на друга и, соответственно, возникновения взаимозависимых сбоев [13]. Поэтому монопольное исполнение одной версии в один момент времени, как при использовании блоков восстановления, в данном контексте является наиболее предпочтительным.

ЗАКЛЮЧЕНИЕ

Метод блоков восстановления позволяет значительно сократить количество используемых ресурсов при исполнении программы по сравнению с мультиверсионным подходом, поскольку если все тесты были пройдены успешно у первой версии, использование альтернативных алгоритмов не потребуется. Однако в случае нахождения ошибки временные издержки могут превышать таковые при использовании, например, метода мультиверсионного программирования.

Также, как уже было отмечено выше, последовательное исполнение блоков позволяет сократить количество используемых вычислительных мощностей, потребляемых в единицу времени, а также снизить вероятность возникновения взаимозависимых ошибок в исполняемых версиях за счёт отсутствия разделения ими общих ресурсов.

Другой сильной стороной метода блоков восстановления, в отличие от того же метода мультиверсионного программирования, является тот факт, что блокам восстановления не требуется программная разработка по единой спецификации, поскольку тесты для каждого блока пишутся индивидуально, что обеспечивает большую экономическую эффективность данного подхода. Кроме того, зачастую к алгоритмам голосования мультиверсионной среды исполнения предъявляются более жесткие требования, чем к приемочному тесту для блока восстановления [10].

Теоретический анализ метода блоков восстановления, а также проведённый эксперимент, показали, что данный подход обладает значительным количеством преимуществ по сравнению с другими подходами повышения надёжности ПО. Несмотря на то, что публикаций по данной тематике на сегодняшний день выходит относительно мало, по мнению авторов, данный метод имеет хорошие перспективы для дальнейшего развития и применения его для решения практических задач.