Метод дерева решений для расчета процента выполнения плана

Кузьмин О.В.; Малышева М.А.; Kuzmin O.V.; Malysheva M.A.

doi:10.18101/2304-5728-2024-1-28-36

Научные статьи \ Математика. Естественные науки \ Математика

Метод дерева решений для расчета процента выполнения плана

Автор: Кузьмин О.В., Малышева М.А.

Журнал: Вестник Бурятского государственного университета. Математика, информатика @vestnik-bsu-maths

Рубрика: Математическое моделирование и обработка данных

Статья в выпуске: 1, 2024 года.

Бесплатный доступ

Сегодня в условиях неопределенности и нестабильности экономической ситуации в мире для предприятий важным параметром является качественный финансово-хозяйственный анализ. Неотъемлемой частью данного анализа является сравнение плановых и фактических показателей компании, таких как доходы, расходы, прибыли, убытки. Наиболее сложным является сравнение прибылей (убытков) в относительных величинах (в процентах), так как именно данный показатель может быть положительным, отрицательным или нулевым. В ходе исследования получены формулы для расчета экономического показателя «процент выполнения плана» для всевозможных значений (положительных, отрицательных, нулевых) плановых и фактических данных с учетом различного соотношения их друг к другу. По результатам работы построена блок-схема, которая позволяет оперативно получать нужную формулу или заданное значение процента выполнения плана для любых входных данных.

Еще

Блок-схема, дерево решений, граф, план-фактный анализ, плановые показатели, фактические показатели, процент выполнения, соотношение плана и факта, экономический показатель, прибыль

Короткий адрес: https://sciup.org/148328494

IDR: 148328494 | УДК: 51-7, | DOI: 10.18101/2304-5728-2024-1-28-36

The decision tree method for calculating the percentage of plan completion

Today, in the face of uncertainty and economic instability worldwide, accurate financial and economic analysis is essential for businesses. One crucial part of this analysis involves comparing planned indicators with actual indicators from a business, such as income, expenses, profits, and losses. The most challenging aspect of this comparison lies in comparing profits or losses as percentages, as these figures can be positive, negative, or even zero. During our research, we developed formulas to calculate the economic indicator «percentage of plan completion» for all possible combinations of planned and actual data. Based on the results of the work, a flowchart has been created, which allows users to quickly calculate a required formula or set a percentage value for completion of a plan based on any given input data.

Еще

Текст научной статьи Метод дерева решений для расчета процента выполнения плана

В последние годы неуклонно растет интерес к теории «больших систем», с которыми приходится иметь дело в самых различных областях науки и техники. Важным направлением исследования таких «больших» или «сложных» систем является рассмотрение их как многоуровневых систем или систем с иерархической структурой [1; 2]. Процесс поэтапного построения решения многокритериальных задач с иерархическими структурами часто может быть интерпретирован как траектория на конечной решетке [3–5], описывающая соответствующее ему частично упорядоченное множество [6].

В монографии [7] предложена схема построения комбинаторных чисел и полиномов на основе иерархической пирамидальной структуры с весами, названной обобщенной пирамидой Паскаля. В [8] широко известная техника теории частично упорядоченных множеств Рота — Стенли [4] применяется для исследования целого ряда комбинаторных объектов, описываемых схемой [7].

Первые идеи создания «деревьев решений» восходят к работам П. Ховленда (P. Hoveland) и Е. Ханта (E. Hunt) конца 50-х гг. XX в. Самая ранняя и наиболее известная из них — основополагающая монография Ханта и др. [9], давшая импульс развитию этого направления.

Построение «деревьев решений» (классификации) — один из основных и наиболее эффективных в настоящее время инструментов интеллектуального анализа данных и предсказательной аналитики. Он помогает в решении задач классификации и регрессии, а также задач, в которых отсутствует априорная информация о виде зависимости между исследуемыми данными. Иерархическое строение дерева классификации — одно из наиболее важных его свойств. Деревья принятия решений с успехом применяются в задачах диагностики и прогнозирования [10–12].

В данной работе, относящейся к области разработки методов анализа иерархических систем и их приложений в задачах принятия решений в экономических задачах [13; 14], строится дерево решений для нахождения важного экономического показателя «процент выполнения плана».

1 Постановка задачи

Крупные компании в процессе своей финансово-хозяйственной деятельности занимаются не только составлением отчетов по фактическим данным, но и формируют финансовый план на определенный период, называемый бюджетом. В бюджете планируются все доходы и расходы, которые предполагает получить и понести соответственно компания в течение периода, на который составляется бюджет.

После утверждения бюджета у компании есть эталон развития событий, но это не значит, что финансово-хозяйственная деятельность компании будет следовать прописанному плану. Каждый месяц компания делает так называемый план-фактный анализ, то есть сравнивает отклонения факта от плана и разбирает причины этих отклонений.

Отклонения бывают в абсолютных величинах и в относительных (процентах). И если в абсолюте вариант расчета только один — факт минус план, то при расчете относительного показателя компания сталкивается со сложностями из-за различного отношения к нулю и друг к другу пла- нового и фактического показателей. В основном это касается показателей прибыли (убытка), так как сами по себе доходы всегда больше нуля, а расходы всегда меньше нуля. Относительный показатель может выражаться либо в процентах выполнения плана, либо в приросте от плана. Показатель прироста получается путем вычитания ста процентов (100%) из процента выполнения. В данной статье получены формулы для расчета процента выполнения.

2 Построение дерева принятия решений

В таблице 1 представлены варианты того, как могут соотноситься показатели плана и факта (P — План, F — Факт):

Таблица 1

№	P	F	Соотношение P и F
1	>0	>0	P=F
2	>0	>0	PHF
3	>0	<0	1 P=FI
4	>0	<0	PHF
5	>0	=0
6	<0	=0
7	<0	>0	1 P=F\|
8	<0	>0	1 p^FI
9	<0	<0	P=F
10	<0	<0	PHF
11	=0	=0
12	=0	>0
13	=0	<0

Итак, возможно 13 вариантов развития событий. Как можно заметить, три из них (а именно, когда факт равен плану: № 1, 9, 11) — это выполненный план, когда процент выполнения равен 100% (табл. 2).

Таблица 2

№	P	F	Соотношение P и F	Расчет процента выполнения, %
1	>0	>0	P=F	100
2	>0	>0	PHF
3	>0	<0	1 P=F\|
4	>0	<0	1 Pffl
5	>0	=0
6	<0	=0
7	<0	>0	1P=F I
8	<0	>0	1P HF I
9	<0	<0	P=F	100

№	P	F	Соотношение P и F	Расчет процента выполнения, %
10	<0	<0	PHF
11	=0	=0		100
12	=0	>0
13	=0	<0

Следующими вариантами для рассмотрения будут случаи, когда один из двух показателей равен нулю, а другой — нет (№ 5, 6, 12, 13). Возьмем за истину то, что если ожидаемая сумма положительная, а факт равен нулю, то процент выполнения будет равным 0%. Если же план отрицательный, а факт привели к нулю, то процент выполнения возьмем за 200%.

Если же получаем варианты, когда планировали показатель, равный нулю, а получили отличный от нуля, то при положительном показателе факта процент выполнения равен 200%, а при отрицательном — (-100%) (табл. 3).

Таблица 3

№	P	F	Соотношение P и F	Расчет процента выполнения, %
1	>0	>0	P=F	100
2	>0	>0	P^F
3	>0	<0	1PHFI
4	>0	<0	1 PHFI
5	>0	=0		0
6	<0	=0		200
7	<0	>0	1 PHFI
8	<0	>0	1 PHFI
9	<0	<0	P=F	100
10	<0	<0	PHF
11	=0	=0		100
12	=0	>0		200
13	=0	<0		–100

Далее рассмотрим вариант, когда план и факт имеют разные знаки (№ 3, 4, 7, 8). Отдельно выделим пограничные случаи, при которых план и факт равны по модулю. Исходя из всего вышесказанного, получаем, что в случае, когда положительным числом являются плановые данные, выполнение плана будет равно -200% (т. е. произошло ухудшение ожидаемых данных ровно на столько, на сколько должно было произойти его выполнение). А в случае, когда план отрицательный, а факт положительный, выполнение плана равно 300%. Эти же результаты можно получить, используя формулы соответственно:

F-P

------x 100 , (1)

P ^,

P-F ------+ 1 x 100 . (2)

P )

Применяя данные формулы, получаем расчеты для вариантов 4 и 8 соответственно (табл. 4).

Таблица 4

№	P	F	Соотношение P и F	Расчет процента выполнения, %
1	>0	>0	P=F	100
2	>0	>0	P≠F
3	>0	<0	\|P\|=\|F\|	F-P - 200 =-----x 100 P
4	>0	<0	\|P\|≠\|F\|	F-P -----x 100 P
5	>0	=0		0
6	<0	=0		200
7	<0	>0	\|P\|=\|F\|	(P-F 300 = -----+ 1 x 100 I P )
8	<0	>0	\|P\|≠\|F\|	(P-F -----+ 1 x 100 I P )
9	<0	<0	P=F	100
10	<0	<0	P≠F
11	=0	=0		100
12	=0	>0		200
13	=0	<0		–100

Остались варианты развития событий, когда плановый и фактический показатели одного знака (либо положительные, либо отрицательные). В случае, когда оба показателя больше нуля, используем стандартную формулу для нахождения отклонения в процентах:

— x 100 . (3)

Заметим, что формула (3) подходит и для вариантов 1 и 9.

Случай, когда оба показателя (план и факт) меньше нуля, разбиваем на 2 варианта: |P|>|F| и |P|<|F|. Для первого работает формула (2), а для второго (выделим его в № 10.1) применима формула:

F-pS

1-- x 100 . (4)

— )

Заполним оставшиеся ячейки в таблице 5.

Таблица 5

№	P	F	Соотношение P и F	Расчет процента выполнения, %
1	>0	>0	P=F	F 100 = — x 100 P
2	>0	>0	P≠F	F — x 100 P
3	>0	<0	1 P=FI	-200
4	>0	<0	1P №F\|	F-P -----x 100 P
5	>0	=0		0
6	<0	=0		200
7	<0	>0	1P=F 1	300
8	<0	>0	1P №1	(P-F -----+1 x 100 I P )
9	<0	<0	P=F	F 100 = — x 100 P
10	<0	<0	\|P\|>\|F\|	(P-F -----+1 x 100 I P )
10.1	<0	<0	\|P\|<\|F\|	( F-PA 1-- x 100 I — )
11	=0	=0		100
12	=0	>0		200
13	=0	<0		-100

Для проверки адекватности получаемых результатов при использовании формул и значений процентов выполнения, приведем дополнительный столбец, в котором обозначим ожидаемые проценты выполнения при данных показателях плана и факта:

Таблица 6

№	P	F	Соотношение P и F	Расчет процента выполнения, %	Ожидаемый про цент выполнения
1	>0	>0	P=F	100	[100%]
2	>0	>0	P#F	F — x 100 P	[>0% и #100%]
3	>0	<0	1P=F 1	F-P -----x 100 P	[-200%]

№	P	F	Соотношение P и F	Расчет процента выполнения, %	Ожидаемый про цент выполнения
4	>0	<0	1 P MF\|	F-P -----x 100 P	[<-200%]или [>-200% и <-100%]
5	>0	=0		0	[0%]
6	<0	=0		200	[200%]
7	<0	>0	1 P=F\|	(P-F -----+ 1 x 100 I P )	[300%]
8	<0	>0	1 P^FI	(P-F -----+ 1 x 100 I P )	[>200% и #300%]
9	<0	<0	P=F	100	[100%]
10	<0	<0	1P MF 1	(P-F -----+ 1 x 100 I P )	[>100% и <200%]
10.1	<0	<0	1P	( f-pA 1-- x 100 I F )	[>0% и <100%]
11	=0	=0		100	[100%]
12	=0	>0		200	[200%]
13	=0	<0		-100	[-100%]

Таким образом, получили несколько вариантов нахождения показателя «процент выполнения плана» в зависимости от соотношения плановых и фактических показателей по отношению друг к другу и к нулю, но табличный вид неудобен для оперативного расчета. Поэтому построим на основе разбора всех возможных случаев и получения исчерпывающих

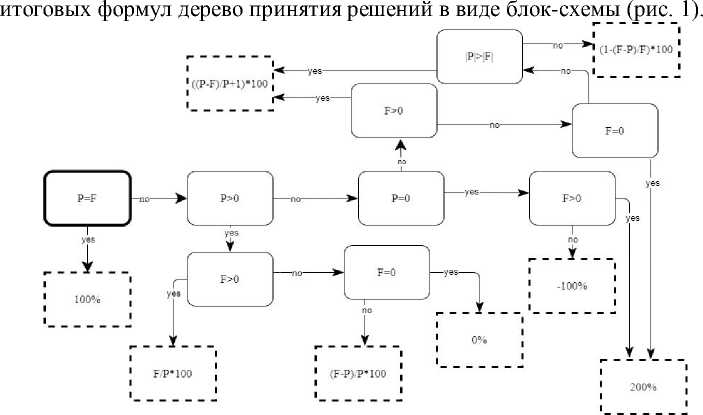
Рис. 1. Дерево принятия решений для расчета показателя «процент выполнения плана»

Ячейка, выделенная жирным — это начало расчета. Ячейки, выделенные пунктиром, — это конечные значения или формулы для расчета показателя «процент выполнения плана». Ветви дерева обозначены двумя значениями: «yes» или «no». Для того чтобы рассчитать показатель «процент выполнения плана», необходимо задать значения плана (P) и факта (F) и пройти по узлам дерева, отвечая «ИСТИНА» (yes) или «ЛОЖЬ» (no) для заданных значений выражения в узлах дерева.

Заключение

Результатом исследования стало построение дерева решений в виде блок-схемы, с помощью которого возможен расчет экономического показателя «процент выполнения плана» при любых заданных плановых и фактических значениях. В работе приведено конечное и исчерпывающее количество формул и значений рассматриваемого показателя. Интегрируя данное дерево принятия решений в финансово-хозяйственный анализ, компания оперативно может получать план-фактный анализ процента выполнения плана по любому экономическому показателю (например, по прибыли) с любым объемом данных. Дальнейшее развитие исследования состоит в разработке программы для ЭВМ по построению данной экономической модели на основе дерева решений.

Список литературы Метод дерева решений для расчета процента выполнения плана

Месарович М., Мако Д., Такахара И. Теория иерархических многоуровневых систем. Москва: Мир, 1973. 344 с.
Саати Т. Принятие решений. Метод анализа иерархий. Москва: Радио и связь, 1993. 278 с.
Стенли Р. Перечислительная комбинаторика. Москва: Мир, 1990. 434 с.
Биркгоф Г. Теория решеток. Москва: Наука, 1984. 568 с.
Гретцер Г. Общая теория решеток. Москва: Мир, 1982. 456 с.
Балагура А. А., Кузьмин О. В. Обобщенная пирамида Паскаля и частично упорядоченные множества // Обозрение приклад. и пром. математики. 2007. Т. 14, Вып. 1. С. 88–91.
Кузьмин О. В. Обобщенные пирамиды Паскаля и их приложения. Новосибирск: Наука. Сиб. издат. фирма РАН, 2000. 294 с.
Kuzmin O. V., Balagura A. A., Kuzmina V. V., Khudonogov I. A. Partially ordered sets and combinatory objects of the pyramidal structure. Advances and Applications in Discrete Mathematics. 2019; 20 (2): 229–242.
Hunt E. B., Janet Marin, Philip J. S. Experiments in Induction. N. Y.: Academic Press, 1966. 247 p.
Кузьмин О. В., Голиков В. А. Применение метода «Дерево решений» в диагностике неисправности двигателя внутреннего сгорания автомобиля // Современные технологии. Системный анализ. Моделирование. 2021. № 2 (70). С. 113–120. DOI: 10.26731/1813-9108.2021.2(70).113-120.
Кузьмин О. В., Мартьянов В. И. Комбинаторно-логические методы анализа иерархических структур и разработка интеллектуальных систем поддержки принятия решений. Иркутск: Изд-во Иркут. гос. ун-та, 2022. 199 с.
Kuzmin O. V. Generalized Pascal's pyramids and decision trees. Advances and Ap- plications in Discrete Mathematics. 2022; 34: 1–15. DOI: 10.17654/0974165822039.
Вотякова Л. Р., Нурумбетова Л. Р. Применение дерева принятия решений в экономических задачах // Тенденции развития науки и образования. 2019. Вып. 49–2. С. 29–32. DOI: 10.18411/lj-05-2019-75.
Панягина А. Е. Использование метода «дерево решений» для оценки кредитного риска // Экономика и менеджмент инновационных технологий. 2013. № 9. URL: https://ekonomika.snauka.ru/2013/09/2978 (дата обращения: 10.02.2024).

Еще