Метод для согласованного выполнения семейства распределенных асинхронно взаимосвязанных транзакций

• 1.    Введение

• 2.    Обзор работ по тематике исследования

  • 2.1.    Свойства алгоритмов ТП

• 2.2.    Обнаружение конфликтов конкурентного выполнения распределенных транзакций

В 90-х годах прошлого века M. Herlihy и J. E. B. Moss описали оригинальную аппаратную реализацию [1] синхронизации доступа нескольких процессоров к разделяемой памяти: конкурентные операции чтения/записи разделяемой памяти процессора могут объединяться в некоторый атомарный (неделимый) набор действий — транзакцию — и выполняться совершенно независимо от операций других процессоров. Предложенный механизм синхронизации, который в настоящее время является объектом активных научных исследований, был назван транзакционной памятью, ТП (англ. transactional memory, TM). Однако можно отметить, что сама идея не так уж и нова: впервые применять подобный механизм синхронизации для любых вычислительных процессов вообще, а не только для управления доступом к данным в базах данных (БД), предложил D. B. Lomet. В своей работе [2] Lomet описал концепцию атомарных действий (англ. atomic actions), позже реализованную Liskov и Scheifler в языке распределенного программирования Argus [3]. Появление идеи транзакционной памяти стало результатом обработки и осмысления многолетних исследований в области традиционной синхронизации вычислительных процессов и моделей согласованности памяти с одной стороны: схожие принципы и соответствующие конструкции можно встретить у Хоара — концепция мониторов [4], и с другой стороны — в области теории транзакционной обработки данных в базах данных.

В настоящее время актуальными являются исследования возможностей и преимуществ применения механизмов транзакционной памяти для масштабируемых вычислительных систем с распределенной памятью, в первую очередь для кластерных вычислительных систем. В силу своих особенностей ТП может оказаться более эффективным и масштабируемым по сравнению с традиционными решениями на основе алгоритмов распределенного взаимного исключения подходом к синхронизации в таких системах, что уже подтверждает ряд имеющихся исследований [5–7].

Свойством живости [8] для алгоритмов транзакционной обработки данных является критерий согласованного выполнения транзакций или просто критерий согласованности.

Примером может служить классический критерий сериализуемости транзакций БД [9]. Однако, из-за существующих различий между транзакциями в БД и транзакциями памяти, прежде всего из-за большей автономности последних, традиционного критерия сериализуемости, который является основополагающим для транзакций БД, не хватает для определения корректности выполнения набора транзакций памяти. В нем рассматриваются лишь зафиксированные транзакции и не затрагивается вопрос корректности выполнения “живых”, еще не зафиксированных транзакций. При использовании оптимистичных методов синхронизации такой критерий подходит только для полностью контролируемых сред или песочниц, какой является для транзакций СУБД, и не является удовлетворительным для транзакций памяти. Действительно, при конкурентном выполнении набора транзакций возможны ситуации гонок и, как следствие, несогласованные чтения: как из-за чередования конкурентных операций, так и, возможно, из-за несогласованного состояния памяти в случае использования клонирования (кэширования) данных, либо механизма откатов (см. классические проблемы конкурентного выполнения транзакций [10]), а валидация (обнаружение конфликтов по данным) происходит только перед самой фиксацией транзакции. Транзакции, выполняемые в еще не обнаруженном состоянии гонок, называются транзакциями-зомби [11] или обреченными (англ. doomed).

С целью избежания подобных ситуаций для алгоритмов ТП был предложен более строгий в плане корректности выполнения критерий, который является вариантом строгой сериализуемости, названный критерием скрытности (англ. opacity) [12]. Он предполагает, что: а) все операции, выполненные каждой зафиксированной транзакцией, представляются так, как если бы они были выполнены в одной неделимой точке жизненного цикла транзакции; б) ни одна операция любой прерванной транзакции не должна быть видна другим, в том числе выполняющимся транзакциям; в) каждая транзакция в любой момент времени наблюдает согласованное состояние системы (невозможны несогласованные чтения). Можно сказать, что критерий скрытности последовательно упорядочивает не только зафиксированные, но и прерванные транзакции, без наблюдения результатов их выполнения другими транзакциями набора. Таким образом, при возникновении конфликт должен быть сразу обнаружен (например, с помощью проверки на наличие изменений версий прочитанных ранее значений), и одна из конфликтующих транзакций прервана и перевыполнена заново.

Одним из самых важных вопросов помимо выбора стратегии обнаружения и разрешения конфликтов конкурентного выполнения набора транзакций является реализация метода обнаружения конфликтов. При использовании отложенной стратегии обновления данных существует необходимость в обнаружении только RW-конфликтов, т.к. для записи используется промежуточный буфер (WR-конфликты невозможны), а сама память изменяется только в момент фиксации транзакции. Возникающие при этом “отложенные” WW-конфликты зачастую разрешаются на основе правила “первая фиксация побеждает” (англ. first committer wins, FCW): в момент фиксации транзакция проверяет перезаписываемые ею данные на наличие обновлений, сделанных конкурентными транзакциями, и, при обнаружении таких обновлений, откатывается. Для оптимистичных механизмов синхронизации [13] основной процедурой методов обнаружения конфликтов является валидация (проверка) множества считанных транзакцией значений Rset. Но то, как и когда данную процедуру использовать, зависит от реализуемого для отслеживания конкурентных обновлений разделяемых данных метода обнаружения конфликтов. Подходы, которые применяются в алгоритмах для мультипроцессорных систем, нельзя напрямую использовать для мультикомпьютерной или распределенной транзакционной памяти, РТП (англ. distributed software transactional memory, DSTM).

В работе [6] был предложен метод обнаружения RW-конфликтов с использованием версий для данных и валидации множества Rset путем отслеживания причинно-следственного порядка между операцией чтения транзакции и операциями записи остальных транзакций системы. Для этого авторы предложили специального вида логические часы [14], которые реализованы в виде целочисленного счетчика и подчиняются следующим правилам:

• 1.    если a — успешное событие фиксации транзакции T i ∈ T , выполняемой на узле системы N k , то часы

• 2.    пусть a — событие приема на узле системы N _k сообщения q , с назначенной меткой времени, равной значению часов узла системы N _m в момент события b отправления сообщения q: t _q = C m (b) ; тогда после события a часы C k устанавливаются в значение большее среди текущего значения часов C k и метки t _q :

C k (a) ^ C k ^ C k + 1                            ⁽¹⁾

C k ^ max(C k ,t q )                                 (2)

Сам метод обнаружения конфликтов, названный методом продвижения транзакции (англ. transaction forwarding ) заключается в следующем:

• •    при старте транзакция T i , выполняемая на узле N _k считывает текущее значение часов C _k и сохраняет его в переменной wv ;

• •    транзакция T i продвигает свое стартовое время wv до значения wv ' > wv , т.е. делает присваивание wv = wv ' , только в случае успешной валидации Rset: для всех объектов в Rset их текущая версия сравнивается с wv и, если версия какого-либо объекта превышает wv , то валидация заканчивается неуспешно, а транзакция откатывается;

• •    для чтения удаленного объекта транзакция T i посылает сообщение-запрос на узел расположения объекта N _m ; при получении ответного сообщения q к посланному ранее сообщению-запросу с текущей версией объекта транзакции необходимо продвинуть свое стартовое время wv до значения t q в случае, если wv < t q (см. выражение 2 для логических часов); если же wv ≥ t q , то объект может быть считан безопасно;

• •    при чтении локального объекта, расположенного на узле выполнения транзакции, его версия проверяется и, если она больше, чем wv , то транзакция откатывается;

• •    в момент фиксации транзакция наращивает часы C _k (см. выражение 1) и назначает новую версию для всех перезаписываемых объектов равную новому значению часов C k .

• 3.    Разработка метода обнаружения RW-конфликтов по данным в распределенной системе

  • 3.1.    Модель системы

На базе предложенного метода авторами разработан алгоритм TFA, который по производительности превосходит все существующие конкурентные решения [6] и, как заявлено авторами, соответствуют критерию скрытности транзакций. Однако это не совсем так. Представим ситуацию, иллюстрация к которой изображена на рисунке. В системе из четырех узлов: ( N i , N 2 , N 3 , N 4 ) выполняются две транзакции T и T 2- При этом транзакция T 2 перезаписывает между R i (z) и R i (v) считанный ранее T объект у , но в момент чтения R 1 ( v ) продвижения транзакции и, следовательно валидации Rset не происходит, в силу того, что wv i = C 4. В результате чтение R i (v) получается несогласованным.

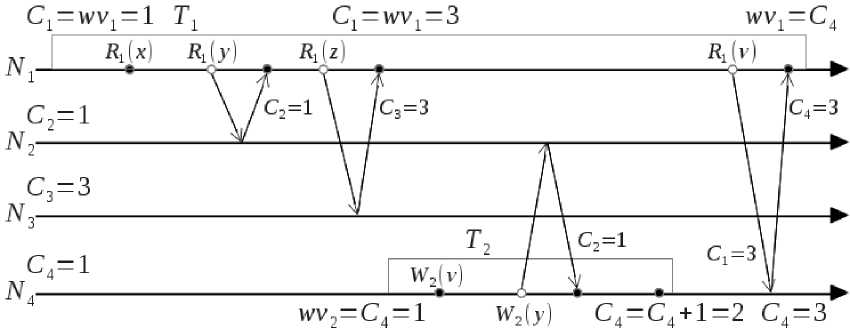
Ситуация несогласованного чтения при использовании метода продвижения транзакции

Кроме этого, недостатком предложенного подхода является его ориентированность на распределенные протоколы когерентности кэша (например Relay [15]), которые плохо масштабируются, и предоставление всего одной перезаписываемой копии объекта транзакциями системы. В работе [7] авторами был предложен подход и ряд принципов для эффективной реализации программно-организуемой транзакционной памяти на основе модели PGAS и односторонних коммуникаций. Предложенный подход был реализован в системе Cluster-STM, хорошо масштабируемой на кластерной системе с сотнями вычислительных узлов. Основной недостаток Cluster-STM — отсутствие поддержки динамического параллелизма на уровне потоков, ограничение “один процессор, одна транзакция” — был устранен в системе GTM [16], также построенной на основе модели PGAS и SPMD-подхода, но вместе с этим предоставляющей поддержку динамического параллелизма на уровне потоков и удаленного вызова процедур. Недостатком обоих систем является предоставление только лишь гарантии сериализуемости; вопрос возможного возникновения гонок и, как следствие некорректное выполнение программы, не рассматривается.

Кроме вышерассмотренных существует ряд подходов, основанных на репликации и мно-говерсионности данных и предоставляющих более слабые по сравнению со скрытностью гарантии согласованности: GMU [17], SCORe [18] и др. Репликация позволяет только читающим транзакциям выполняться локально, без генерации сетевого трафика и валидации удаленных данных. В GMU применяется многоверсионная схема данных, векторные логические часы [19] для отслеживания причинно-следственной связи между событиями, а также частичная истинная схема репликации данных. GMU предоставляет слабый критерий согласованности EUS (англ. extended update-serializability), согласно которому различные только читающие транзакции могут видеть результат обновления неконфликтующих пищущих транзакций в различном порядке. Улучшенная версия протокола частичной истинной репликации данных, который назван SCORe, гарантирует более строгий критерий выполнимой сериализуемости одной копии (англ. executing one-copy serializability, 1CS) [18]. Протокол SCORe достаточно хорошо масштабируем и эффективен за счет использования локальной мультиверсионной схемы данных, позволяющей только читающим транзакциям всегда выполняться без отката, и за счет масштабируемой схемы синхронизации логических часов, в которой связанные транзакции обмениваются лишь одним скалярным числом — меткой часов.

Таким образом, можно сделать вывод, что в настоящий момент не разработано методов и алгоритмов РТП, гарантирующих выполнение критерия скрытности. Разработанные ал- горитмы, дающие более слабые гарантии, реализуются на основе динамических, интерпретируемых языков, таких как Java, которые позволяют обнаружить и, возможно, устранить исключительные ситуации, возникающие из-за несогласованных чтений. Для более популярных в области выскопроизводительных вычислений не динамических языков, таких как C/C++ представлено всего несколько программных средств: Cluster-STM и DMV [20], гарантирующие сериализуемость, и HyflowCPP [21] — программный фреймворк, реализующий алгоритм TFA, который как было показано выше не предоставляет гарантию выполнения критерия скрытности.

Пусть N = { n i , П 2 ,..., n N } — множество узлов распределенной асинхронной вычислительной системы без сбоев [8], а T = { T i , T 2 ,..., Tm } — множество распределенных в системе транзакций . Кроме транзакций система также включает в себя память с последовательной моделью согласованности, с помощью которой транзакции взаимодействуют. Будем подразделять память на два вида:

• 1.    Plmk — приватная , доступная только транзакции T k G T , k = 1,M и относящаяся к или выделенная на узле выполнения T k : n j G N , j = 1,N память. Множество L представляет собой совокупность всей локальной памяти в системе: L = Plm i U Plm 2 U ... U Р1т м ;

• 2.    G — разделяемая , доступная всем транзакциям системы память такая, что G = Pgm i U Pgm 2 U ... U Pgm N , где Pgm j — часть разделяемой памяти, выделенная на узле n j G N , j = 1, N .

Будем считать, что сами транзакции неподвижны и выполняются на том же самом узле, где были инициированы, а удаленные данные при этом могут перемещаться и кэшироваться на узле выполнения транзакции. Подобная модель, которая была предложена в работе [22], называется моделью с потоком данных . Также будем считать, что транзакции используют отложенную стратегию обновления данных.

Память представляет из себя множество специальных объектов — ячеек . Каждой ячейке памяти x соответствует некоторое определенное значение, задаваемое отображением V(x) . Обозначим символом V множество всех возможных значений, которые могут принимать ячейки памяти. Совокупность всех ячеек системы будем обозначать символом M : M = L U G . Будем говорить, что множество ячеек M i равно множеству M 2, когда:

| M 1 | = M Л ( V x G M i 3 !y G M 2 : x = y Л V(x) = V(y))

Для описания системы взаимодействующих распределенных транзакций воспользуемся по аналогии рядом базирующихся на понятии машины состояний определений, предложенных в [8], и адаптируем их для распределенной системы:

Определение 3.1. Локальным алгоритмом транзакции будем называть пятерку (Z, I, bi, br, bw), в которой Z — множество состояний, I — это некоторое подмножества множества Z, bi — отношение на множестве Z х Z, br — отношение на множестве Z х M х Z, bw — отношение на множестве Z х M х V х Z. Двуместное отношение b на множестве Z определяется соотношением:

c b d     (c,d) e b i V3 x E M ((c, x, d) E H r ) V 3 x E M, 3 v E V ((c, x, v, d) E b w )

Отношение H i представляет собой переход между состояниями, связанный с внутренними событиями транзакции T k E T, отношение H r — событиями чтения значения из ячейки памяти, а b w — событиями записи значения в ячейку памяти. Транзакция T k E T может выполняться на любом узле n E N вычислительной системы (ВС). Выполнение транзакции T k — выполнение системы переходов ( Z k , I k , b k , b k , b W ) . Состояние транзакции S T _k описывается собственно состоянием транзакции c T _k и состоянием или слепком доступной ей локальной памяти Plm k : S T k = ( c T _k , Plm k ) . Внутренние события и события чтения, которые описываются с помощью отношений b k , b k соответственно, могут изменять собственно состояние транзакции, а события записи в том числе и состояние доступной ей памяти: как локальной, так и глобальной.

Для описания распределенной системы в целом введем понятие распределенного алгоритма , составленного из соответствующих компонент транзакций, и системы переходов, которую данный алгоритм порождает:

Определение 3.2. Распределенным алгоритмом семейства транзакций T = { T i , T 2 ,..., Tm } будем называть совокупность локальных алгоритмов, каждый из которых соответствует в точности одной транзакции из T .

Состояние семейства транзакций T будем называть конфигурацией . Каждая конфигурация системы определяется состояниями всех транзакций и состоянием разделяемой памяти G .

Поведение распределенного алгоритма семейства транзакций T описывается с помощью системы переходов, определяемой следующим образом:

Определение 3.3. Пусть задано семейство транзакций T =  {T1, T2,..., Tm}, а локальный алгоритм каждой транзакции Tk представлен пятеркой (ZTk, 1тк, bTk, bTk, bTk). Будем говорить, что система переходов S = (C, ^, I) порождена распределенным алгоритмом для семейства асинхронно взаимосвязанных транзакций T, если выполнены следующие соотношения:

• 1.    C = {( S T 1 ,. ..,St _m , G) : ( V T E T : S t E Zt ) A ( V x E L, V y E G : V (x), V (y) E V ) } , где C — множество конфигураций семейства транзакций;

• 2.    ^ = ( [Jt_g t ^ t ) , где символом ^ т обозначаются переходы, которые соответствуют изменениям состояния транзакции T, т.е. ^ T i — множество всех пар вида

(STi, ...,STk , • . . , STm , Gi), (STi,. ..,STk ,•• - , STm ,G2), таких, что выполняется одно из следующих условий:

• •    (S T k ,S T k ) Eb T k и M l = M 2;

• •    для некоторой ячейки x E M i имеется событие чтения ( S T k ,x, S T ) E b T и M i = M 2 ;

• •    для некоторой ячейки x E M i и значения v E V имеется событие записи ( S _{T k} ,x, v, S T _k ) E b T k так, что | M ₁ | = | M ₂ | и 3 !y E M 2 : x = y A V(y) = v;

• 3.    I = { ( St i ,.. .,S t M ,G) :^k(W E T : St E It )

A ( V x E L, V y E G : V (x) = V o (x),V (y) = V o (y),V (x),V (y) EV ) } , где I — множество начальных конфигураций семейства транзакций, а V o (x) : V x E L U G — задает начальные значения ячеек памяти.

Соответственно выполнением распределенного алгоритма называется всякое выполнение системы переходов, которая порождена этим алгоритмом. Конкретное выполнение E задается в видет последовательности конфигураций, через которые система проходит в данном выполнении: E = ( y o , Y i , • • • ) • Выполнение может быть либо конечным, если для него имеется заключительная конфигурация, т.е. такая конфигурация y € C : ^ | Y ^ ^ , либо бесконечным, если для него заключительной конфигурации не существует. С выполнением E связана последовательность событий E = (e o ,e 1 ,...) , где e i — некоторое допустимое событие, обозначающее преобразование конфигурации Y i в Y i +1: e i (Y i ) = Y i +1.

Очевидно, что если два последовательных события в выполнении влияют на не пересекающиеся подмножества конфигураций, то эти события независимы и могут “выполняться” в другом порядке. В противном случае, если события нельзя поменять местами, то между ними существует причинно-следственная зависимость . Для любой последовательности событий E , связанной с некоторым выполнением E выделим три вида такой зависимости.

Определение 3.4. Будем говорить, что между двумя событиями e i , e j € E существует:

• 1.    истинная зависимость: e i 4^wr e j ^^ событие e i — событие записи в некоторую ячейку x € M значения v € V , а событие e j — последующее после e i событие чтения из ячейки x значения v;

• 2.    выходная зависимость: e i 4 ^ww e j ^^ событие e i — событие записи в некоторую ячейку x € M значения v 1 € V , а событие e j — последующее после e i событие записи в эту же ячейку x значения V 2 € V ;

• 3.    антизависимость: e i 4 ^rw e j ^^ событие e i — событие чтения из некоторой ячейки x € M значения v i € V , а событие e j — последующее после e i событие записи в эту же ячейку значения v 2 € V .

По аналогии с отношением причинно-следственного порядка, которое Лэмпорт ввел для систем с асинхронным обменом сообщениями [14], зададим такое же отношение для описанной выше асинхронной системы с распределенной общей памятью.

Определение 3.5. Причинно-следственное отношение частичного порядка Ч на множестве событий системы E выполнения E — это такое наименьшее отношение, удовлетворяющее следующим трем условиям:

• 1.    если e и f — два события одной транзакции и e произошло раньше, чем f , тогда e Ч f; 2. пусть e и f два разных события, тогда если e Ч^ШТ f V e 4 ^ww f V e 4 ^rw f, то e Ч f;

• 3.    отношение Ч транзитивно, то есть если e Ч g и g Ч f, то e Ч f.

• 3 .2. Метод обнаружения RW-конфликтов по данным в распределенной системе

Определим два вида специальных событий, допустимых при выполнении распределенного алгоритма семейства транзакций. Первый вид событий — событие отката A k : такое допустимое событие в последовательности событий транзакции T k Е т _к = ( e o , • • •, e i , A k , e 0 ,...) | Е т _к C E , представленное парой A k = ( S T , S T ) €H T , что A k (Y i +i ) = Y o, где Y o = ( St i ,• • •, S T _k ,•••, St m ,G^ : S T _k € L j k \ ( V x € Plm k : V ( x ) = V o ( x ) € V ) • Второй вид специальных событий — событие фиксации C k транзакции T k : такое допустимое событие в последовательности событий Е т _к = (e o , • • •, e i , C k ) , представленное парой C k = ( Sir , ST ) € Ну, , что S T — заключительное состояние T k в выполнении E .

T k T k       T k          T k

Будем считать, что с каждой ячейкой x : x G G связана некоторая версия или метка ts X : ts k G TSset , присвоенная x транзакцией T k . Определим на множестве TSset функцию TS такую, что:

TS : TSset ^ {(j, tsn) : j G Z+, tsn G Z^o} , где j — целое положительное число, номер узла ВС n G N, а tsn — целое неотрицательное число, которое является отметкой времени часов узла nj .

Определим, аналогично тому, как это сделано в работе [6], логические часы CLK _m для узла ВС n m G N:

• 1.    если C k — успешное событие фиксации транзакции T k G T, выполняемой на узле системы n _m , то

• 2.    пусть e — событие чтения ячейки x G G транзакцией T k G T, выполняемой на узле системы n m ; при этом если ячейке назначена версия ts x : TS ( ts x ) = ( j, tsn ) , тогда после события e часы CLK _m устанавливаются в значение большее среди текущего значения часов CLK _m и отметки tsn версии ts _x :

CLK m ( C k ) ^ CLK m ^ CLK m + 1                  (3)

CLK m ^ max(CLK m , tsn)                        (4)

Установим следующие соотношения для всех возможных значений версий ячеек ts i G TSset. Пусть V ts 1 ,ts ₂ G TSset : TS ( ts 1 ) = ( j 1 ,tsn 1 ) Л TS ( ts 2 ) = ( j ₂ ,tsn ₂ ) , тогда выполяня-ется:

ts 1 =, <, > ts ₂ ^^ tsn 1 =, <, >  tsn ₂ , ts 1 < , >  ts ₂ ^^ tsn 1 < , >  tsn ₂ , ts 1 = ts ₂ ^^ tsn 1 = tsn ₂ Л j 1 = j ₂ , ts 1 ^, ^ ts ₂ ^^ ts 1 <, >  ts ₂ V ts 1 = ts ₂

Определим множество прочитанных ячеек транзакции T k как: Rset k = { x | x G G Л 3 e : e G Е т _к Л e — событие чтения ячейки x } . На множестве Rset k зададим функцию RS k : Rset k ^ { ts | ts G TSset } — версия ячейки, которой соответствует некоторое значение v G V . Таким образом RS k ( x ) = ts x .

Определим для каждой транзакции T k вектор VC k : | VC k | = | N | = N так, что j — й элемент вектора равен VC k [j] = tsn — некоторой отметке времени логических часов узла с номером равным j . Предлагаемый метод обнаружения RW-конфликтов в распределенной системе предполагает использование отложенной стратегия обновления данных и заключается в следующем:

• •    при старте транзакции T k , выполняемой на узле n m , вектор VC k инициализируется нулевыми значениями: VC k [i] ^ 0, V i = 1, N ;

• •    при чтении значения ячейки x G G с соответствующей версией ts x G TSset : TS ( ts x ) = ( j, tsn ) проверяется, если VC k [j] <  tsn, то производится валидация объектов Rset k и присваивание VC k [ j ] ^ tsn, а также изменяются часы CLK m (см. выражение 4 для логических часов); конфликты отсутствуют и объект может быть считан безопасно только в случае успешной валидации после чего в Rset k добавляется x : RS k (x) = ts x ;

• •    при записи ячейки x G G производится определение ее текущей версии и при необходимости изменяются часы CLK m согласно выражению 4, а новое значение v сохраняется в буфере для последующей записи во время фиксации (отложенная стратегия обновления данных);

• •    валидация производится для всех объектов x чьи версии сохранены ранее в Rset k путем сравнения текущей версии объекта ts ' x относительно сохраненной в Rset k версии ts x : RS k (x) = ts x и если ts ' x >  ts x , то валидация заканчивается неуспешно ;

• •    в момент события C k фиксации транзакции T k , выполняемой на узле n m , наращиваются часы CLK _m (см. выражение 3), а все объекты атомарно перезаписываются новым значением v ' с новой версией равной ts k = ( m, CLK m (C k ) ) .

• 4.    Программная реализация предложенного метода

Сформулируем и докажем следующее утверждение:

Теорема 3.1. Предложенный метод при условии атомарной перезаписи новыми значениями ячеек памяти во время фиксации транзакций позволяет гарантированно обнаруживать во время выполнения распределенного семейства асинхронно взаимосвязанных транзакций RW-конфликты по данным, которые могут привести к ситуации несогласованного чтения.

Доказательство. Допустим, что это не так. Тогда для некоторой транзакции T _k узла ВС n _m в выполнении E распределенного алгоритма, реализующего предложенный метод, существует событие несогласованного чтения e" ячейки y G G с версией ts y G TSset : TS ( ts y ) = ( j, tsn s ) и VC k [ j ] >  tsn s , т.о. после e " валидация Rset k не производится. При этом в выполнении E для T k есть также предшествующее событие чтения е ' ячейки x G G с версией, созданной транзакцией T r , ts rx G TSset : TS ( ts ^r x ) = ( i,tsn r ) такое, что e ' -< e " .

Существование события несогласованного чтения e " ячейки y G G означает то, что 3 два события записи f ' и f " транзакции T s узла n : f ' — событие записи ячейки x G G , а f" — событие записи ячейки y G G с соответствующими версиями ts X ,ts y G TSset : TS(tsX) = TS ( ts y ) = ( j, tsn s ) Л ts X > ts rx . Причем при условии атомарности перезаписи новыми значениями ячеек памяти во время фиксации транзакций выполняется: 1) e ' ^ rw f ' , e" ^^тш f '' , либо 2) e ' ^ rw f ' , f '' X w e". При этом f ' -< f ” V f '' -< f ' . В первом случае событие e '' не является событием несогласованного чтения, что противоречит первоначальному условию.

Во втором случае, так как после события чтения e '' выполняется соотношение VC k [j] >  tsn s , то для транзакции T k должно 3 событие чтения g ячейки z G G с версией ts Z G TSset : TS ( ts⁴ q ) = ( j, tsn q ) Л VC k [ j ] = tsn q >  tsn s . Т.е. ts Z произведена некоторой транзакцией T q . Тогда, если tsn ^q = tsn ^s , то T q — это и есть транзакция T _s , поэтому при чтении ячейки z G G валидация Rset _k должна отследить изменение версии ячейки x G G и дальнейшее событие несогласованного чтения e " невозможно: т.о. приходим к противоречию. Если tsn q > tsn s , то T _q и T _s разные транзакции одного узла ВС n j , но T _q завершилась позже T _s , следовательно, валидация Rset k после события чтения g также должна отследить изменение версии и ячейки x G G , следовательно дальнейшее событие несогласованного чтения e '' невозможно. Опять приходим к противоречию.

Стоит отметить, что условие атомарной перезаписи ячеек памяти при фиксации транзакции обычно выполняется в силу использования специальных протоколов фиксации, таких как двухфазный протокол фиксации (2PC).

На основе разработанного метода предложены алгоритмы и создана программная система распределенной транзакционной памяти DSTM_P1 [23, 24]. Данная система реализована на языке C++ и предназначена для запуска и контроля над выполнением многопоточных приложений, написанных на языке Си с использованием метода синхронизации на основе распределенной кэшируемой программно-организуемой транзакционной памяти, на кластерных вычислительных системах под управлением операционной системы Linux.

DSTM_P1 можно условно разделить на две основные части: среду выполнения приложений и прикладной программный интерфейс (API), доступный для написания многопоточных приложений. Среда выполнения является своего рода программной “песочницей” для приложений пользователя и, по выбору пользователя. API системы DSTM_P1 подразделяется на:

• •    интерфейс для работы с распределенной разделяемой памятью Idstm_mal loc;

• •    интерфейс для запуска и управления выполнением распределенных потоков Idstm_pthread;

• •    интерфейс для барьерной синхронизации распределенных потоков Idstm_barrier.

• 5.    Заключение

Общая схема работы DSTM_P1 может быть описана следующим образом: (1) пользователь системы загружает исходные коды многопоточного приложения, написанного на языке C с использованием библиотеки Pthread и применением атомарных конструкций (__tm_atomic) в местах доступа к разделяемым данным; (2) приложение компилируется с помощью DTMC [8] в язык промежуточного представления; (3) далее полученное представление трансформируется в представление, содержащее соответствующие вызовы функций библиотеки транзакционной памяти для всех инструкций доступа к памяти атомарного блока; (4) представление, полученное на предыдущем шаге линкуется с необходимыми библиотеками (транзакционной памяти, «обертками» системных библиотек pthread и malloc); (5) на лету компилируется и исполняется main-функция приложения; (6) все вызовы функций библиотеки pthread и malloc переадресуются в соответствующие вызовы функций библиотек «оберток». Во время исполнения main-функции при вызове pthread_create определяется код функции потока, который распределяется в системе с помощью модуля балансировки нагрузки и исполняется в отдельном потоке на менее загруженном узле кластера.

С предварительными результатами экспериментальных исследований можно ознакомиться в [24].

В работе представлено описание метода, который может быть использован для разработки алгоритмов синхронизации конкурентного выполнения набора распределенных асинхронно взаимосвязанных транзакций. Отличительной особенностью метода является его соответствие строгому критерию согласованности транзакций: критерию скрытности.