Метод дополнительного поля для синтеза фокусаторов

Расчет Фазы фокусатора

Рассмотрение проводится в одномерном случае, хотя обобщение на двумерный случай не встречает дополнительных трудностей. Пусть требуется рассчитать функцию пропускания фазового элемента ехр[1ф(х)], где х£[-а,а], который плоскую волну фокусирует на расстоянии z в отрезок у £ [”b,b] с заданным распределением интенсивности 1(у). Пусть функция пропускания фокусатора и требуемая интенсивность связаны преобразованием Фурье вида a iф(х)   -1 т— ху

Ку) =

—/ е е Л dx

V Хг -а

Из (1) следует [8], что функция Ку) должна быть целой аналитической функ цией конечного порядка экспоненциального вида. Поэтому вместо функции Ку) нужно исходить из некоторой аналитической функции Ку), которая, во-первых, в избранных отсчетах совпадает с исходной функцией 1(у), а, во-вторых, имеет следующую асимптотику нулей

Az .

yn - 21 п " Ап где 1(уп) = 0- Добиться этого можно, например, используя теорему отсчетов Котельникова [8] .

Так как фаза поля в области фокусировки может быть произвольной ф(у), уб[-Ь,Ь], то получаем для комплексной амплитуды света в области фокусировки выражение

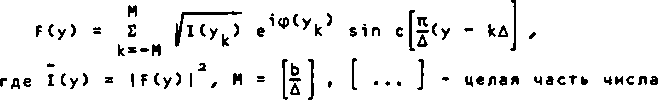
Фазу ф(у) лучше выбирать случайной величиной, что будет способствовать более равномерному распределению амплитуды в плоскости фокусатора.

Итак, вместо требуемой интенсивности в плоскости фокусировки должно формироваться поле F(y). Заметим, что поле F(y) не ограничено отрезком [-b,b]z а отлично от нуля на всей оси - ” <у< “ , то есть из ограниченного отрезка [-а,а] фокусатора нельзя полностью всю энергию сосредоточить в конечном отрезке [~b,b] . "Дефект" энергии, очевидно, равен величине

Ь_

D = / I(y)dy - /” I(y)dy.(4)

Обратный Фурье-образ поля F(y)

ie(x) „ i^xy

Ф(х) = А(х) е = / F(y)edy.

благодаря выбранной частоте отсчетов Д, будет финитной функцией и сосредоточен на отрезке [-а,а]. Однако нет гарантии, что поле Ф(х) будет чисто фазовым. Не постоянство амплитуды А(х) создает определенные трудности при создании оптических элементов с амплитудно-фазовой функцией пропускания ФСх) (см., например, [9]>.

Если амплитуда А(х) была бы постоянной величиной, то такой оптический эле мент можно было бы реализовать по технологии изготовления киноформов. Для того чтобы создать чисто фазовое пропускание фокусатора, введем дополнительное поле вида В(х)е , удовлетворяющее условию

А(х)е1в(х) ♦ В(х)е’шх = е1ф(х). (6)

Из (6) следует выражение для искомой фазовой функции фокусатора

ф(х) = arctg

А(х) sin 8 (х) * В(х) sin (ох) А(х) cos в (х) * В(х) cos (ox)

где В(х) = [1 - А3(х) sin2(6(x) - ох)]^ - А(х) cos (в(х) - ох).              (8)

Из (8) видно, что амплитуда дополнительного поля меняется в диапазоне О < В(х) £ 2/ если А(х) S 1.

Величина выбирается из условия неперекрытия Фурье-образов от полей А(х)е^^Х^ _ iox и Be и удовлетворяет неравенству о 5

4пЬ

Az

Если не проводить замену 1(у) на I Су) , то после первого Фурье-лреобразования (из области фокусировки в плоскость фокусатора) часть световой энергии попадет за пределы отрезка фокусатора [-а,а], а после второго Фурье-преобразования (из отрезка фокусатора в плоскость фокусировки) еще часть световой энергии попадет за пределы отрезка фокусировки [-b,b], что приведет к увеличению степени искажения восстановленного распределения интенсивности по сравнению с исходным.

Численные результаты

Предложенный метод апробировался численно. Исходная интенсивность выбиралась в виде

Ку) =

1. у £ [-Ь, Ь] о у У[-ь, ь] .

Дискретность в плоскости фокусатора равна Н = 0,1 мм, а в плоскости фокусировки И = (NH)-1 (N - общее число отсчетов в обеих плоскостях). Вместо Д в дискретном варианте выбиралась величина На = (2N1H)  , где 2N1H - ширина фокуса тора (ширина области фокусировки равна 2b = 2N Н1). Случайная фаза ф(у) моделировалась датчиком случайных чисел, равновероятно заполняющих отрезок значений

S S 1 7' 7]

. Последовательность действий следующая. Строятся отсчеты функции

F(y) по формуле (3), к F(y) применяется обратное быстрое преобразование Фурье и получаются отсчеты функции Ф(х), далее по формуле (7) определяются отсчеты фазы фокусатора ф(х), строится функция пропускания ехр[:ф(х)], к которой применяется прямое быстрое преобразование Фурье. Восстановленное распределение интенсивности сравнивается с исходным (10),

Так как фаза дополнительного поля выступает в качестве несущей частоты для Фазовой функции фокусатора, то на данном ниже рис.1а, б, в видно, что в плоскости Фокусировки формируется распределение интенсивности, состоящее из трех "порядков" дифракции. Минус первый порядок (левый на рис. 1) - это восстановленное исходное распределение интенсивности, нулевой порядок (центральный на рис. 1) -Фокусировка от дополнительного поля, плюс первый порядок (правый на рис. 1) -восстановленное исходное поле, искаженное из-за взаимодействия с дополнительным полем. На рис. 1 показано распределение интенсивности в плоскости фокусировки при следующих параметрах эксперимента: N =w128, N1 = 64, S = 10, со = 1 4 мм 1, Н = 0,1 мм, Na = 2 (рис. 1а), Na = 4 (рис. 16), Na = 8 (рис. 1в). Энергетическая эффективность, то есть процентное отношение энергии света, попавшей в область фокусировки шириной 2NaH1, ко всей энергии света, было равно 8% (см. рис. 1а), 12$ (см. рис. 16), 7% (см. рис. 1в).

На рис. 2 показана фаза фокусатора для случая, представленного на рис. 16. Причина искажения восстановленной интенсивности связана с интерференцией вторичных лепестков соседних порядков. Причина невысокой энергетической эффективности фокусировки в том, что амплитуда А(х) в пределах отрезка [-а,а] меняется в большом диапазоне значений от 0,01 до 1, а в тех точках, где АСх) мало, амплитуда В(х) приближается к своему максимальному значению. То есть, чем больше будет "провалов" функции А(х) до нуля, тем меньше будет энергетическая эффективность. Это подтверждает рис. За, б, где изображены сформированные фокусаторы Распределения интенсивности в плоскости фокусировки при следующих параметрах: N = 128, Na = 2, Н = 0,1 мм/ <о=5 мм-1, S = 15, N, = 64 (рис. За), N, = 32

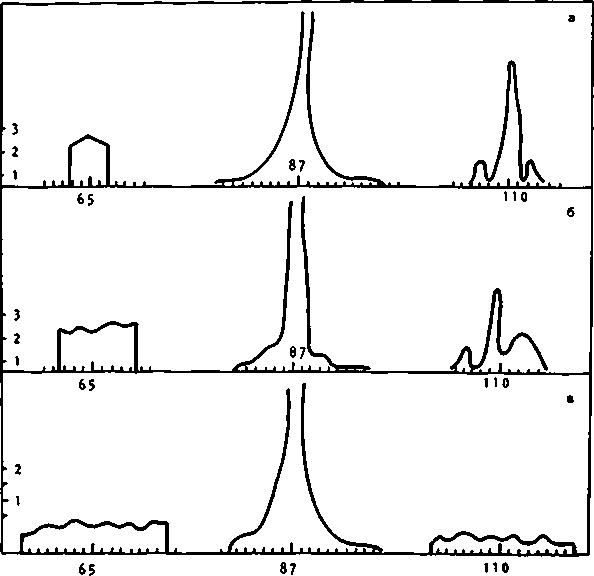
Рис . 1

- -2

■ -з

Рис. 2

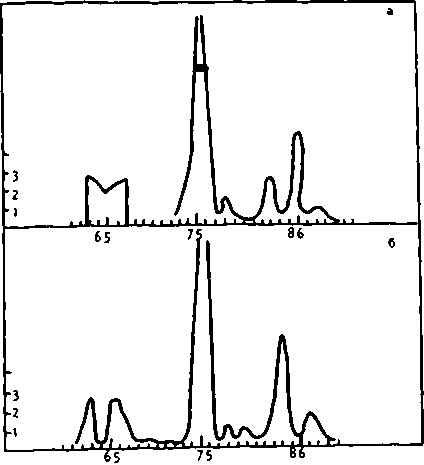
Рис. 3

(см. рис. 36). Энергетическая эффективност ь для случая, представленного на рис. За, составляет 123, на рис. 36 - 8%. Видно, что при уменьшении апертуры фокуса-тора эффективность растет, но увеличивается степень искажения вида исходной интенсивности. Эффективность растет при уменьшении N1, потому что на меньшем отрезке [-а,а] амплитуда А(х) меняется в меньшем диапазоне, а искажение вида интенсивности при уменьшении Ni происходит из-за того, что амплитуда А(х) становится отличной от нуля за пределами отрезка [-а,а].

Уменьшения диапазона изменения амплитуды А(х) в пределах отрезка [-а,а] и тем самым повышения эффективности фокусировки можно добиться увеличением дисперсии случайной фазы исходного поля, то есть увеличением величины S. На рис. 4а, б, в показаны только требуемые части восстановленной интенсивности в плоскости фокусировки при параметрах N₁ = 64, N₂ = 2, w = 14 мм ¹, S = 1 (рис. 4а) ,  5 = 4

(рис. 46), S = 10 (рис. 4в). Энергетическая эффективность соответственно равна 53, 5,4 и 73.

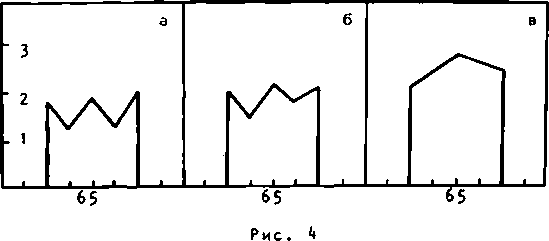
Заметим (см. рис. 1), что с наименьшими искажениями восстанавливается вид исходной интенсивности, когда область фокусировки близка к дифракционному пределу.