Метод фазово-частотного спектрального анализа электрокардиосигнала в задачах домашней телемедицины

Проблемы, относящиеся к сердечно-сосудистым заболеваниям, всегда носили злободневный характер и по статистике являются причиной 57 % общей смертности в России. В связи с этим задачи разработки высокоэффективных методов диагностики состояния сердца приобретают все большую актуальность.

Благодаря развитию систем автоматизированной обработки электрокардиосигнала (ЭКС), у нас есть возможность разработать концептуально новые медико-диагностические приборы, спроектировать и отладить канал связи для беспроводной передачи данных и проанализировать состояние сердца, используя портативный анализатор аритмий.

В данной работе рассматриваются ЭКС здоровых людей и людей, у которых присутствует нарушение сердечного ритма, а именно нарушение морфологии QRS-комплекса, которое принято называть экстрасистолой. А также другие параметры сердечного ритма, которые могут отличаться в зависимости от вида аритмии или состояния человека. Например, это могут быть параметры, характеризующие изменения P и T зубца и вариабельность сердечного ритма. В данной работе рассмотрим такие виды аритмий как бигеминия, тригеминия и пароксизмальная наджелудочковая тахикардия:

• •    Нарушение сердечного ритма называют бигеминией тогда, когда экстрасистолы следуют в строгом порядке за каждым циклом основного ритма,

то есть фиксируется чередования синусовых и экс-трасистолических циклов в соотношении 1:1.

• •    Тригеминия фиксируется в двух ее проявлениях, а именно:

• 1.    Две парные экстрасистолы, которые следуют подряд за одним циклом основного ритма. В таком случае фиксируется чередование синусовых и экстрасистолических циклов в соотношении 2:1. И данный вариант расценивается как наиболее опасный и более сложный вид патологии.

• 2.    Второй вариант, когда экстрасистолы идут подряд за двумя циклами основного сердечного ритма и фиксируется их соотношение 1:2.

• •    Пароксизмальная наджелудочковая (в дальнейшем ПНТ) тахикардия обладает признаками: ЧСС от 100–250 ударов в минуту. Зубец Р может предшествовать желудочковому комплексу, может сливаться с комплексом QRS или следовать за ним, а также может отличаться по форме, амплитуде и по полярности в сравнении с синусовым ритмом [4].

Для автоматического анализа ритма сердца необходимо владеть информацией не только о длительностях последовательных RR-интервалов, но и информацией о форме QRS-комплексов (морфологии). При этом, задача сводится к точному выявлению является ли очередной QRS-комплекс нормальным или же является патологическим [2].

Для разработки алгоритма различения ЭКГ-сигналов на основе спектральных параметров QRS-комплекса и параметров других элементов

LM^^e © щербакова Т.Ф. и др., 2019

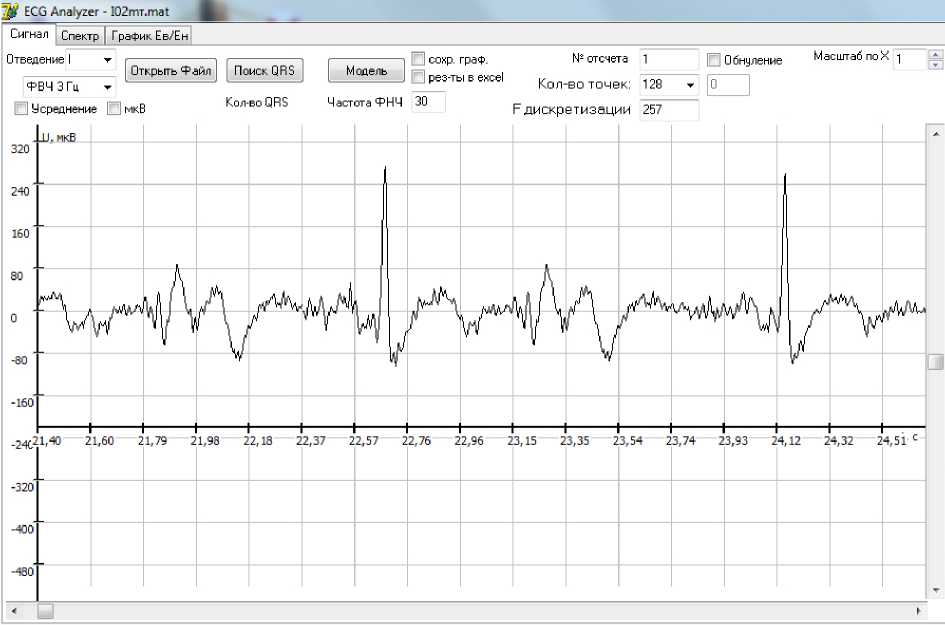
Рис. 1. Исходный ЭКГ сигнал (бигеминия)

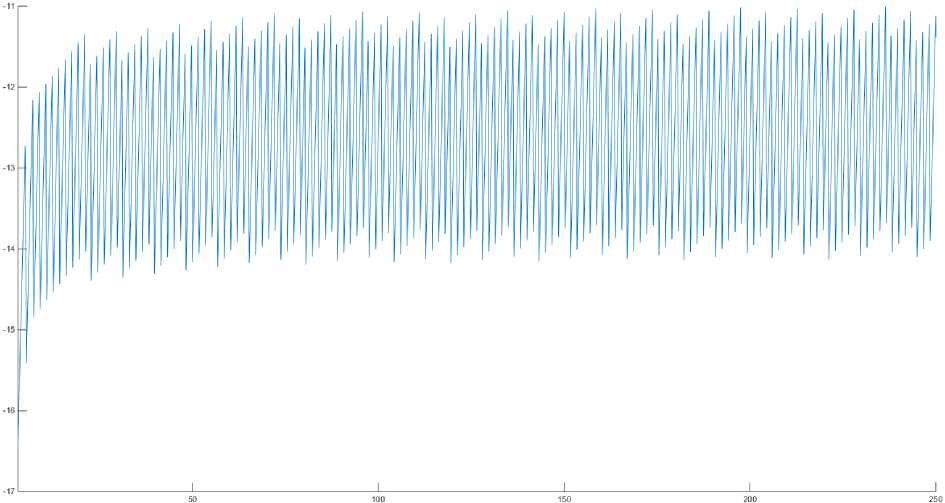
Рис. 2. Фазово-частотный спектр ЭКГ сигнала с бигеминией

ЭКС (Р и Т зубцы), а также параметров вариабельности сердечного ритма нужно определить пороги принятия решения [1].

Наш алгоритм обнаружения аритмий и дальнейшего их различения имеет следующий порядок действий:

• •    С помощью быстрого преобразования Фурье (БПФ), проводимого с участками ЭКС длительно-

• стью 1 минута, мы получили их спектры. Построение фазовых спектров проводилось для ЭКС с патологией и ЭКС здорового человека.

• •    Построение графиков отношения энергий высокочастотной (ВЧ) части спектра к низкочастотной (НЧ).

• •    Нахождение математических ожиданий и дисперсий отношений энергий ВЧ части спектра к НЧ.

  

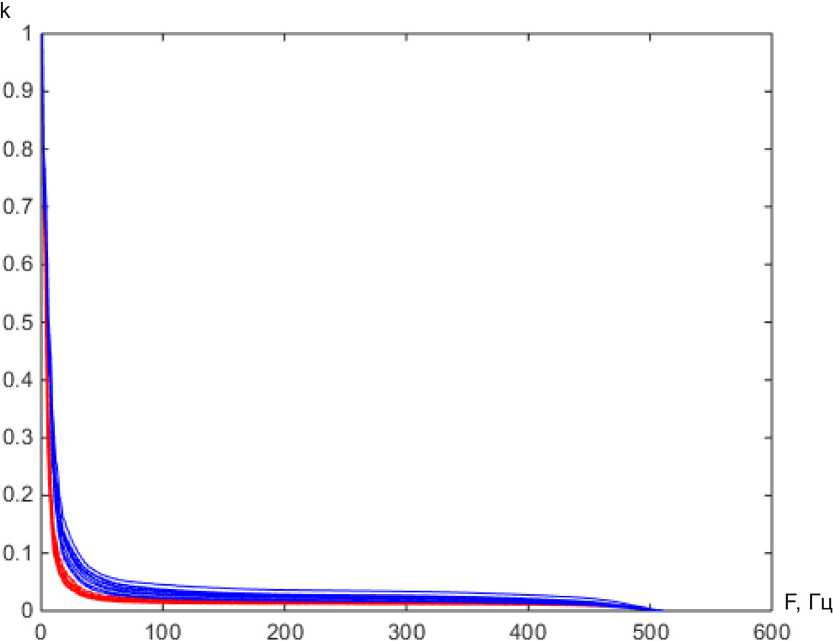
  Рис. 3. Изменения коэффициента K от f _гр. Верхняя группа – норма; нижняя – бигеминия

  
  

• Построение гистограмм распределений для непосредственного определения порога принятия решения.

• Реализация автоматического определения по- рога принятия решения с помощью аппаратных средств Matlab.

Для анализа использовали 40 реализаций ЭКС, взятых из базы данных ресурса PhysioNet [3]. При- мер исходного сигнала и его спектр представлены на рис. 1 и 2 соответственно.

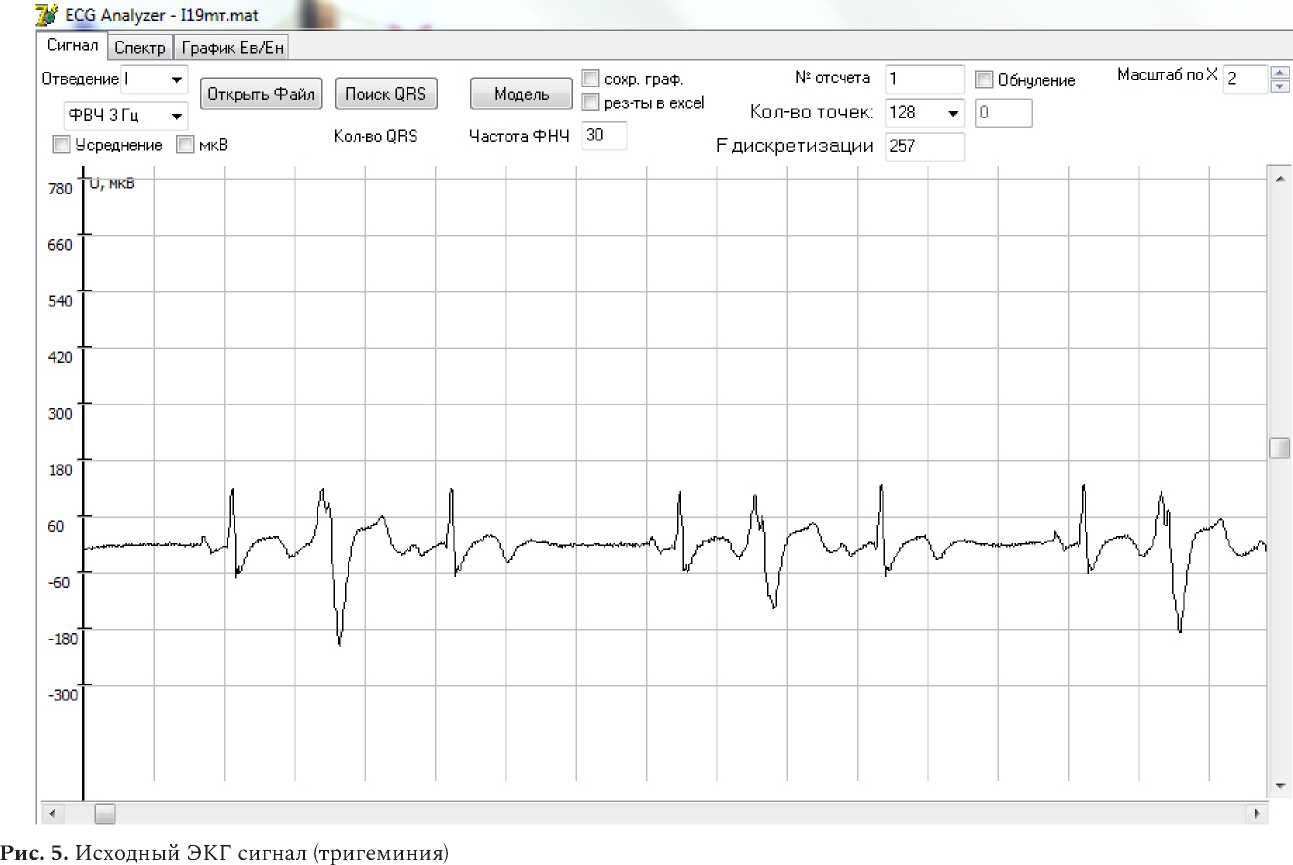
Как мы видим из иллюстраций, используемых ЭКГ-сигналов, чередование паталогических и нормальных QRS-комплексов фиксируется в соотношении 1:1, что доказывает наличие нарушения сердечного ритма, а именно наличие бигеминии [3].

Для автоматизированной фиксации различий в спектрах ЭКС в норме и с приведенными выше аритмиями, мы предлагаем ввести коэффициент, представляющий собой отношение суммарных амплитуд высокочастотной части спектра к его низкочастотной части:

f 'р

Z U i iz —   i = 0

K = -500—

Z Ui i - f'P+1

.

Значения этого коэффициента существенным образом зависят от граничной частоты f _гр между высокочастотной и низкочастотной частями спектра сигнала. Далее мы для каждого значения f _гр от 5 Гц до 150 Гц с шагом 1 Гц вычисляли коэффициенты K для всех исследуемых ЭКС. Зависимость

K от f _гр для двух классов представлены на рис. 3. Для каждой f _гр получаются разные распределения K для случаев нормы и бигеминии. Нам необходимо найти оптимальное значение f _гр, при котором распределения K наиболее значимо различаются.

Для решения этой задачи построим гистограммы распределений коэффициента K при каждой f _гр, и аппроксимируем гистограммы гауссовскими плотностями распределения вероятностей (рис. 4). Используем суммарную вероятность принятия ошибочного решения p ₂ в качестве численного критерия различия распределений K для разных классов ЭКС.

K пор + 3 ^ 0

p ₂ = p ( S ₀)    j w ( K | S ₀) dw +

K пор

K пор

+ P ( ^ i )    j w ( K | ^ i ) dw .

K пор - 3 ^ 1

Здесь S0 и S1 – классы ЭКС в норме и ЭКС с бигеминией; p(S0) и p(S1) – доли количества случаев нормы и бигеминии соответственно в общем ко- личестве исследованных случаев.

Мы полагаем оптимальным то значение граничной частоты f гр , при котором p ^ будет минимальным. Все построения мы провели с помощью программы Matlab, В результате получили оптимальную граничную частоту f 'р = 20 Гц. Гистограммы распределений коэффициента K для данного случая представлены на рис. 4.

Для распределений рис. 4 определим пороговое значение коэффициента K по критерию мак-

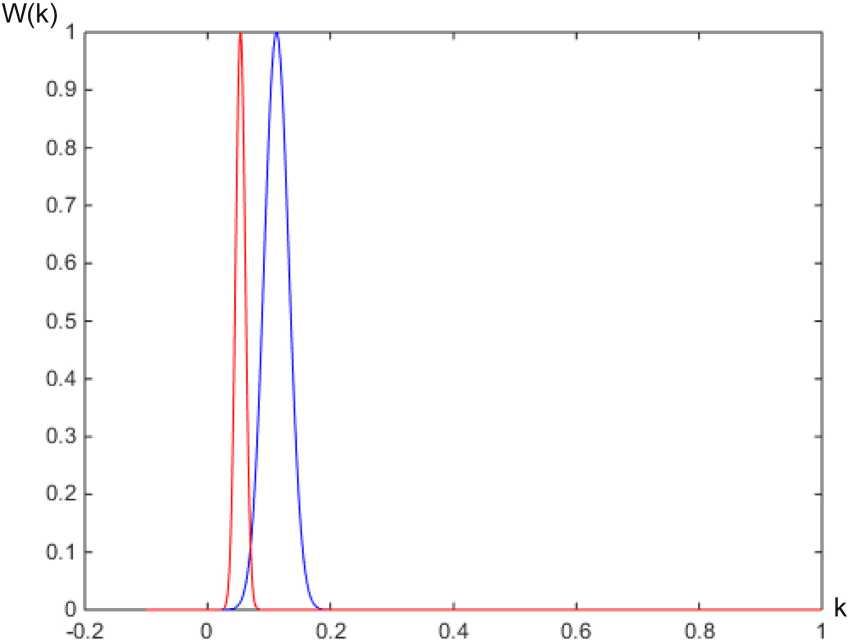
Рис. 4. Аппроксимация гистограмм распределений коэффициента K (справа норма, бигеминия слева)

симального правдоподобия. Оно соответствует точке пересечения распределений с координатами k _nop |^0,07;0,11084 ] . Суммарная вероятность принятия ошибочного решения при этом составит: составила p s о = 0,00089396; p s 1 = 0,00035393; P s общ = ^0,00035³⁹³.

Применим теперь точно такой же подход для определения тригеминии. Для анализа мы ис- пользовали 40 реализаций ЭКС с наличием данной аритмии, взятых из базы данных ресурса PhysioNet [4]. Один из сходных ЭКГ сигналов с тригеминией приведен на рис. 5.

Аналогичный анализ определения порога принятия решения был проведен для сравнения ЭКС здорового человека и человека с тригеминией. Были получены графики отношения ВЧ/НЧ, представленные на рис. 6.

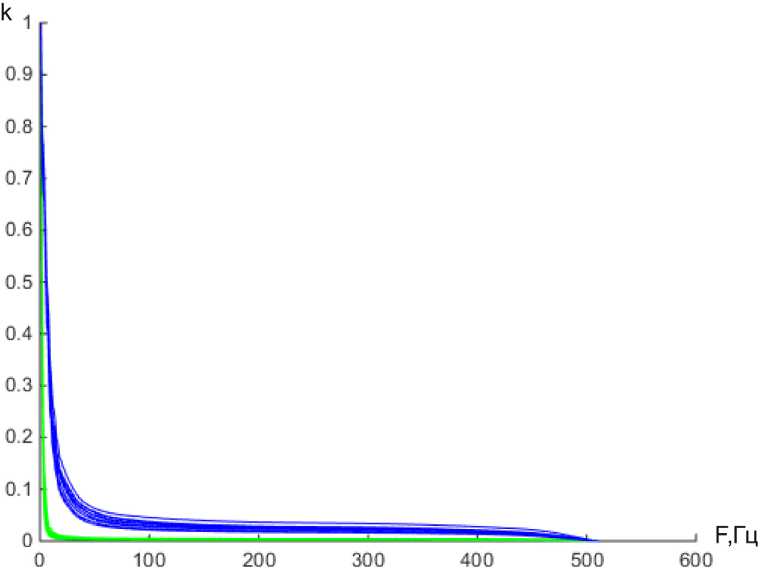
Рис. 6. Изменения коэффициента K от f _гр. Верхняя группа – норма; нижняя – тригеминия

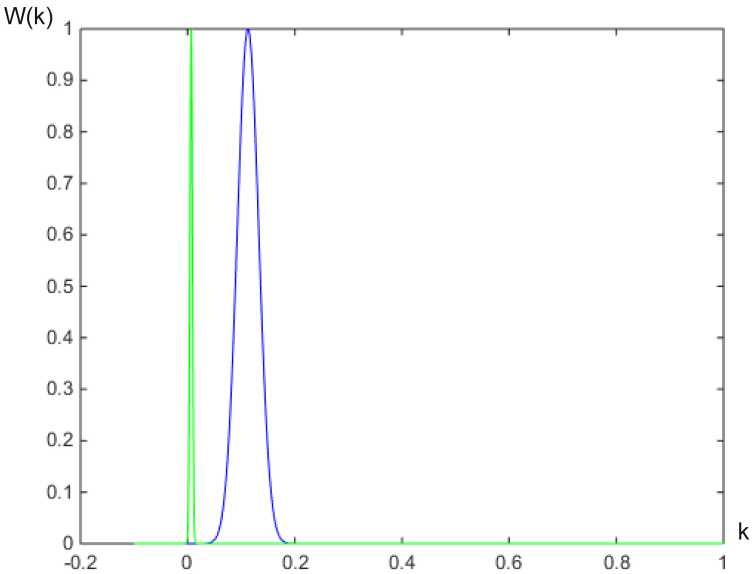
Рис. 7. Аппроксимация гистограмм распределений коэффициента K (справа – норма, слева – тригеминия)

Построим гистограммы распределений. Таким образом, мы эмпирически определили минимальную площадь под пересечением «кривых» и удалось достичь наилучшего различения групп сигналов при f _?р = 25 Гц. При этом точка пересечения распределений будет соответствовать точке с координатами к _по р [ 0,0169;0,00001334 ] . Вероятность ошибки для распределений рис. 7 составила p s ₀ = 0,0000078356; p s 1 = 0,0000085495; p_{s общ} = = 0,0000163851.

Аналогичным образом определим порог принятия решения между нормой и пароксизмальной наджелудочковой тахикардией. Графики отноше- ния высокочастотной части спектра к низкочастотной представлены на рис. 8.

Получим распределения плотностей вероятностей коэффициента K для двух классов S ₀ норма и S ₁ – пароксизмальная наджелудочковая тахикардия (рис. 9). Данный пример приведен также для случая минимальной суммарной вероятности принятия ошибочного решения при анализе ПНТ.

При этом p s 0 = 0,00005264; p s 1 = 0,000087451; p s _о б _щ = 0,00014009. Точка пересечения распределений имеет координаты к _по р [ 0,0403;0,0016648 ] . Суммарная вероятность ошибки для распределений рис. 10 при f _Г р = 23 Гц является минималь-

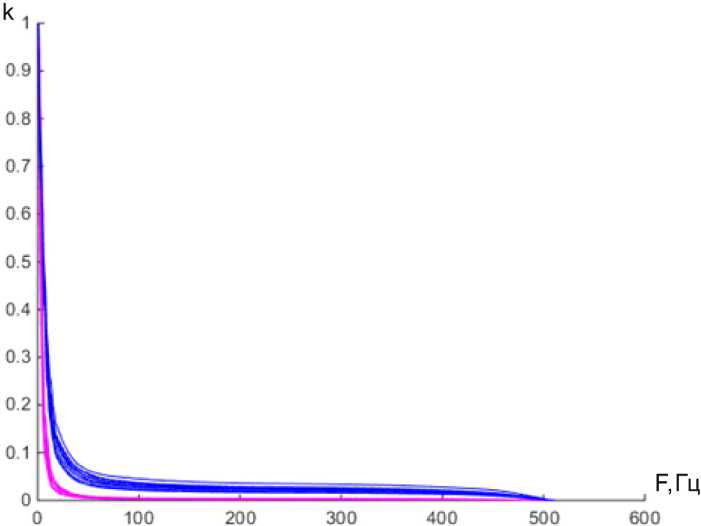
Рис. 8. Изменения коэффициента K от f _гр

. Верхняя группа – норма; нижняя – ПНТ

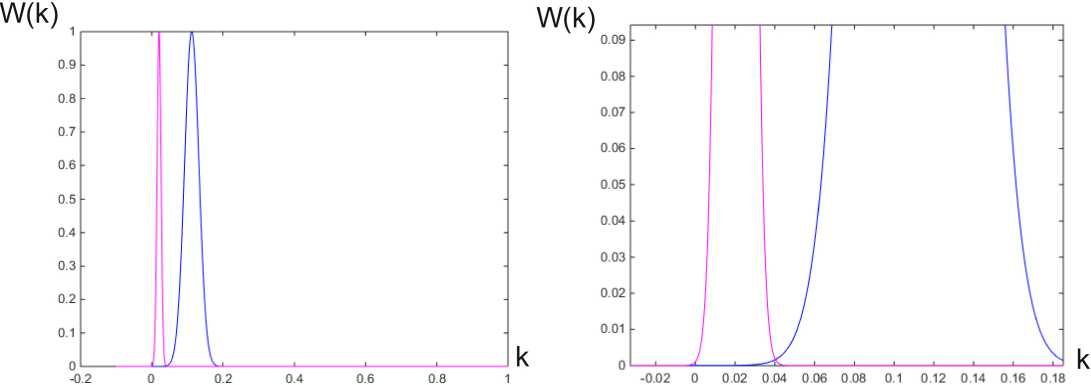
Рис. 9. Аппроксимация гистограмм распределений коэффициента K (справа – норма, слева – ПНТ)

Тригеминия ПНТ       Бигеминня Норма

Рис. 10. Положение порогов принятия решения на одной числовой оси ной. Поэтому соответствующее значение кпор считаем оптимальным для нашего исследования и принимаем его как исходное для дальнейших исследований данного вида аритмии.

Выделим диапазоны для точного принятия решения в пользу той или иной аритмии. Ранее было получено и показано, что в случае с бигеминией порог к = 0,07; в случае с тригеминией порог к = 0,0169; и в случае с пароксизмальной наджелудочковой тахикардией порог составлял к = 0,0403. Продемонстрируем это на одной числовой оси (рис. 10).

Все k , которые попадают в промежуток 0,0403 ^ 0,007 будут однозначно определять принадлежность отклонения сердечного ритма к бигеминии; коэффициенты k из промежутка 0,0169 ^ 0,0403 будут относиться к пароксизмальной наджелудочоковой тахикардии; и, соответственно, коэффициенты, попавшие на отрезок 0 ^ 0,0169, будут определять принадлежность к тригеминии.

Ранее нами было проведено исследование использования амплитудного спектра ЭКС для построения графиков отношения ВЧ/НЧ и их ап-

Таблица

Сравнительная таблица полученных результатов

Название аритмии Амплитудно-частотный спектральный анализ Фазово-частотный спектральный анализ Вероятность ошибки, pу Коэффициент, k Вероятность ошибки, pу Коэффициент, k Норма-Бигеминия ps общ = = 0,0025154 кпор[0,0698;0,11688] ps общ = = 0,00035393 k пор [0,07;0,11084] Норма-ПНТ ps общ = = 0,002118 кпор[0,0362;0,01794] ps общ = = 0,00014009 кпор [0,0169;0,00001334] Норма-Тригемния ps общ = = 0,0018325 кпор[0,0342;0,01617] ps общ = = 0,0000163851 кпор [0,0403;0,0016648] проксимации гистограммами распределений и результаты, полученные ранее, дали меньшую точность определения порога принятия решения.

В таблице приведены сравнительные результаты, полученные при амплитудно-частотном спектральном анализе и фазово-частотном.

Таким образом, в результате исследования были выявлены преимущества фазочастоных характеристик по сравнению с амплитудно-частотными характеристиками. А именно, повысилась точность принятия решения по причине уменьшения вероятности принятия ошибочного решения.