Метод гауссовской аппросимации пика спектраотражения волоконно-оптического брэгговского датчика

Волоконно-оптические брэгговские датчики [1] в настоящее время находят применение в различных научных исследованиях и технических приложениях. При этом наличие в настоящее время достаточно мощной вычислительной техники, в том числе цифровых сигнальных процессоров, даёт возможность повышать точность измерений и снижать влияние шума на результат измерений не только за счет совершенствования оптических и электронных узлов, но и за счёт применения специальных методов математической обработки экспериментальных данных.

Информацию о состоянии брэгговского датчика несёт положение брэгговского пика в спектре. Как следствие, основной задачей при обработке брэгговских спектров является задача высокоточного определения положения брэгговского пика в спектре. В качестве основных препятствий, стоящих на пути решения этой задачи, можно отметить две проблемы.

Первая проблема связана с тем, что вводимая в цифровую компьютерную систему информация о брэгговском спектре дискретна по координате. Эта дискретность может быть малой или большой, но полностью избавиться от неё невозможно. Хотя используемые в настоящее время фоточувствительные приборы (например, ПЗС-линейки и другие аналогичные устройства) обладают достаточ но высокой разрешающей способностью, требования к точности измерений нередко оказываются настолько высокими, что требуют определения смещения брэгговского пика с ошибкой на два-три порядка меньшей, чем размер светочувствительного пикселя ПЗС-линейки. Очевидно, что для решения такой задачи недостаточно лишь определить номер пикселя с максимальной освещённостью, здесь требуется применение каких-то специальных математических методов.

Здесь необходимо отметить особую важность исследования вопроса о таких ошибках определения смещения брэгговских пиков, которые не обусловлены шумом во входном сигнале, а принципиально свойственны тому или иному методу и являются реакцией данного метода на пространственную дискретность фоточувствительного прибора. Такие ошибки, для которых в дальнейшем будет использоваться термин ошибки метода, могут быть весьма опасными, так как, с одной стороны, эти ошибки являются систематическими во времени и не исчезают даже при нулевом уровне шума (поэтому их невозможно уменьшить путём усреднения по нескольким реализациям одного и того же спектра), а с другой стороны, величина этих ошибок меняется по мере смещения брэгговского пика вдоль линейки светочувствительных пикселей. Как следствие, ошибки метода могут приводить к тому, что после обработки экспериментальных данных в поведении брэгговского пика могут быть обнаружен некие осцилляторные эффекты, которые в ре альности отсутствуют.

Вторая проблема связана с шумом. Хот брэгговские спектры, как правило, характе ризуются достаточно высоким (30...40 дБ более) отношением сигнал/шум, влияни шума в брэгговских спектрах чаще всег нельзя считать пренебрежимо малым. Одни из путей снижения влияния шума на точност определения смещения брэгговских пико может быть применение каких-либо методо аппроксимации экспериментальных данных, как, например, представленный в данной работе метод гауссовской аппроксимации.

Другим путём снижения влияния шума может быть применение корреляционных методов определения смещения брэгговских пиков [2]. В этом случае алгоритм гауссовской аппроксимации может быть весьма полезен на одном из этапов корреляционных расчётов, а именно, на этапе обработки информации об опорном спектре.

Краткое описание центроид-метода

Так называемый центроид-метод является традиционным и широко применяемым методом обработки данных с волоконно-оптических брэгговских датчиков и, поскольку в дальнейшем результаты применения метода гауссовской аппроксимации (и корреляционных методов, представленных в работе [2]) будут сравниваться с результатами применения центроид-метода, необходимо привести краткое описание данного метода.

На рис.1 показан возможный пример зависимости освещённости от координаты для брэгговского пика. Экспериментальные данные об этом брэгговском пике, получаемые с помощью ПЗС-линейки или другого аналогичного устройства, можно представить в виде гистограммы, где ширина каждого столбца равна ширине пикселя ПЗС-линейки, а высота определяется уровнем освещённости, усреднённым по площади данного пикселя. Для того, чтобы определить положение максимума пика, предположим, что координата максимума совпадает с координатой центра

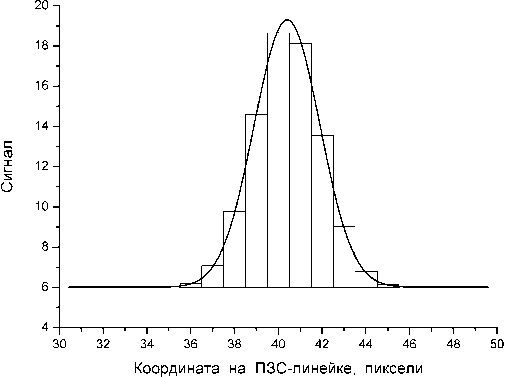
Рис.1. Пример зависимости освещённости от координаты для брэгговского пика и гистограмма, иллюстрирующая расчёт положения пика по центроид-методу

тяжести фигуры, образованной столбцами данной гистограммы, то есть xm

I XiUi

i

I Ui ’

i

где x_i ‒ координата, соответствующая середине i -ого столбца гистограммы, u_i ‒ высота i -ого столбца, то есть амплитуда сигнала с i -ого пикселя ПЗС-линейки.

Здесь необходимо уточнить, что вследствие особенностей схемы электронной части спектрального прибора нулевому уровню освещённости не обязательно должно соответствовать нулевое напряжение на входе АЦП. Поэтому специально необходимо оговорить, что здесь и далее под амплитудой сигнала с i -ого пикселя понимается разность между напряжением, получаемым при опросе этого пикселя, и напряжением, получаемым при опросе полностью затемнённого пикселя (нулевым уровнем или “уровнем чёрного”). На рис.1 этот “уровень чёрного” соответствует шести относительным единицам. Таким образом, амплитуда сигнала, снимаемого с наиболее освещённого пикселя (пиксель № 40) составляет приблизительно 12,7 относительных единиц.

Как будет показано в разделе, посвящённом анализу результатов моделирования, предположение о совпадении координаты максимума пика с координатой центра тяже- сти гистограммы является вполне адекватным и при достаточно большом числе столбцов гистограммы центроид-метод позволяет весьма точно рассчитать положение максимума пика. Кроме того, нельзя не отметить простоту центроид-метода и, как следствие, экономию машинного времени, что особенно важно при счёте “в реальном времени”.

Однако, центроид-метод имеет серьёзный недостаток - достаточно высокую чувствительность к шуму во входном сигнале (конкретные цифры также будут приведены в разделе, посвящённом анализу результатов моделирования). Повышенная чувствительно сть центроид-метода к шуму заставляет искать другие методы обработки брэгговских спектров.

Метод гауссовской аппроксимации пиков брэгговского спектра

Для решения задачи гауссовской аппроксимации брэгговских пиков был применён метод наименьших квадратов. При этом для определения параметров аппроксимирующей функции был использован метод линеаризации задачи и проведение нескольких итераций для определения этих параметров с требуемой точностью. Метод линеаризации и проведения нескольких итераций был ранее успешно применён для обработки данных с измерительных линий СВЧ диапазона [3] и зарекомендовал себя как весьма удобный метод для решения задач аппроксимации с применением вычислительной техники.

Сначала рассмотрим задачу аппроксимации в общем виде.

Пусть имеется массив экспериментальных точек u(x) , где i принимает значения от 1 до N . Требуется найти некоторую функцию f(x, a 1 , a 2 , ..., a m ) , которая наилучшим образом аппроксимирует эти экспериментальные точки. Здесь x - аргумент функции; a 1 , a 2 ,..., a_m - некоторые параметры, которые определяют конкретный вид функции f и которые требуется вычислить в ходе процедуры аппроксимации.

Как известно, метод наименьших квадратов предусматривает в данном случае минимизацию величины х2

Q = £ ( f ⁽ x i , a i , a 2 , - , a m ) — u ⁽ x i ) ) , (2) i = 1

то есть поиск таких значений параметров a₁, a₂, ... , a_m , при которых Q принимает минимальное значение.

Для решения этой задачи требуется решить систему уравнений:

dQ = °. Q = о, ^d a i         d a 2

, IQ- = 0. (3) о a_m

m

Однако, эта система уравнений является нелинейной и её решение может оказаться весьма затруднительным.

Выход из создавшегося положения может быть следующим. На начальном этапе находится так называемое “нулевое приближение” для функции f , то есть без применения метода наименьших квадратов определяются грубые приближения для параметров a₁, a 2 , ... , a m . Эти грубые приближения можно обозначить как a₁₀, a₂₀, ..., a m ₀ .

Для определения более точных значений a1, a 2, ... , ak необходимо с помощью метода наименьших квадратов определить поправки 6^, 6a2,..., 6am, такие, что ai = ai0 + 6ai , a 2 = a 20 + 6a 2,

........., am = am0 + ^am •      (4)

Для определения этих поправок можно разложить функцию в ряд:

f ( x , a _w + 8 a i , a 20 +8 a 2 , ... , a m 0 +8 a m ) =

= f ⁽ x , a io , a 20 , ... , a m 0 ) ⁺

+ dai

a 1 = a 10

• 8 a i

+ f da 2

• 8 a 2 +

a 2 = a 20

d f ^d a m

• 8am am=am 0

Далее для краткости будут использованы следующие обозначения:

/г = f(xi,ai0,a20, ... ,am0), df dak

df dak ak=ak 0, x = Хг ui = u (xi) . (6)

При определении поправок с помощью метода наименьших квадратов необходимо будет выполнить условия минимизации величины

QL = ^ (fl + -/' 8a 1 +      8a 2 + i=1            д a i

+      +      8am - ui )

д am что потребует решения системы уравнений dQ=o, =o, 33axd3a

, -Q- = 0.(8)

ЭК

В отличие от (3), система уравнений (8) является линейной относительно 3a₁ , 3a ₂, ... , 3a_m и её решение не представляет никаких принципиальных сложностей, особенно если речь идёт о решении с применением вычислительной техники.

После определения поправок 3a₁ , 3a ₂, ... , 3a_m по формулам (4) могут быть вычислены уточнённые значения параметров a₁, a₂, ... , a_m , а затем, если это необходимо, может быть проведена новая итерация: полученные значения a₁, a₂, ... , a_m могут быть использованы как a₁₀, a₂₀, ... , a_m0 и описанным выше способом к ним могут быть вычислены новые поправки. Далее этот процесс можно повторить необходимое число раз.

Теперь рассмотрим более частный вариант этой задачи ‒ аппроксимацию брэгговского пика гауссовской функцией.

Определим функцию f как

f (x, ka , xm , °) = ka Ф(X, xm , о), (9) где ka ‒ амплитудный коэффициент, ф(x, xm, о) - функция Гаусса:

1 l x ^- X m

ф(X, Xm , G) =       e- 2 — , (10)

gV2n ^     7

x ‒ координата, измеренная вдоль ПЗС-линей- ки (будет использована безразмерная координата, где в качестве единицы длины использован шаг пикселей ПЗС-линейки), xm ‒ центр гауссовского распределения, характеризующий положение максимума брэгговского пика, о - дисперсия гауссовского распределения, характеризующая ширину брэгговского пика.

Таким образом, параметры k_a , x m , о - это и есть те параметры, которые необходимо определить в ходе процедуры аппроксимации.

“Нулевые приближения” этих параметров могут быть определены следующим образом. В качестве x_m0 может быть использована координата пикселя с максимальным значением амплитуды сигнала (эта амплитуда будет обозначена как A m ). В качестве О ₀ может быть использована величина

^О 0

^А wH 2

2 2 ln2

= 0,425 A w _1/2,

где Aw1/2 - ширина брэгговского пика по уровню 1/2 высоты, вычисленная как разность координат тех пикселей справа и слева от вершины пика, амплитуда сигнала с которых приблизительно равна половине Am . В качестве ka0 может быть использована величина ka 0 = Am О V2^ .

Тогда система уравнений (8) может быть записана в виде:

a113ka + a123xm + a133o = b1,

a 213ka + a223xm + a233o = b 2,     (13)

a ₃₁3k_a + a ₃₂ 3x_m + a₃₃3o = b 3 , где коэффициенты выражаются следующим образом:

nN

an =EФ^ , a12 = kao^Ф.^ ,

1=1      ,               i = 1     ^{d x} m ’

_ i N дф i ^a 13 k a o ^ ^ф i , i = 1     ^dG

V дФ a 21 =L Ф/д , 1=1   dxm ’

, v ^fдф i a 22 = k a o Z

_A ²

i = 1 V ^д x m

V¹ дф₁ a 31 = Z ф^г , ы    до ^,

v ^дф i  ^дф i

, a23 = kao Z^         , i=1 дxm до

v дф i дф i a32 = kao Z^    5"T, i=1 дxm до

После завершения итерационной процедуры по вычисленным значениям параметров k a , X_m , o может быть рассчитана аппроксимирующая функция для данного брэгговского пика:

a ₃₃

N

I ^{дф /} k a o Z l □ i = 1 V ^до )

app ( x )

k a         е 2 oV 2 п	(        3 X - X m	2 (18)
	о V        7

NN b1 = ZUiфi - kaoЕф2 = i =1                     i =1

N

= Е u i ф i — ^k a o a 11 i = 1

или опорная функция для корреляционных расчётов [3]:

д f ref ^{( X} ) = 3- = д X

X m   X   _ — ka   3 г— e 2 о 3 ч2п	(        3 X - X m	2 . (19)
	о <        7

N b 2 = Е ui i =1

^дф i ^д x m

-

N kao Ефi i =1

^дф i ^д x m

V дф i     .

= Z ^U i4k a o a 21 i = 1 ^д x m

Впрочем, необходимо отметить, что в том случае, когда корреляционные методы расчётов не используются, необходимости в расчёте аппроксимирующей функции после завершения итерационной процедуры, как правило, не возникает ‒ достаточно рассчитать значение x_m , которое и будет представлять собой координату максимума брэгговского пика.

V дф b з = Е ui^-i=1 до

-

, V дф i kao Ефi д i=1    до

N

Z u i It до

-

^k a 0 a 31

i = 1

Здесь использованы обозначения, анало-

гичные использованным ранее для общего

случая:

T i = Ф( X i , X m 0 , ^o 0 ) ,

дф i = дф ^д x m ^д x m

^дф i = дф д x_m до

x m x m 0 , x x i

O = O 0 ^, X = X i ’

где

дф

x — x

m

^д x m

o o

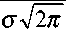
e 1

^X - ^X m

o

V 7

, (16)

дф до

^f ( x ^- x m ⁾²

O3 V

A

о

•

x

- X m

oV 2 n

e 2

о

, (17)

Моделирование брэгговских пиков

Как и любой вновь разрабатываемый алгоритм, метод определения смещения брэгговских пиков с помощью гауссовской аппроксимации нуждается в проверке. В ходе такой проверки необходимо провести сравнение рассчитанного положения брэгговского пика с его действительным положением, причем это сравнение надо будет провести при различных формах пика. Такую проверку представляется целесообразным выполнить с применением численного моделирования, то есть с использованием модельных брэгговских спектров. Такие модельные брэгговские спектры могут быть без особых проблем “сгенерированы”, если необходимо, зашумлены, и, так как эти модельные спектры создаются компьютером в строгом соответствии с указаниями оператора, положение пиков в этом спектре (имеется в виду положение пиков до зашумления спектра) будет точно известно ещё до начала его обработки, что и даст возможность провести сравнение действительного смещения пиков с рассчитанным по той или иной методике.

В качестве модельного пика использовался, во-первых, пик гауссовской формы. На рис.2а показан такой пик с параметром σ , равным 1,5 пикселя, что соответствует ширине пика приблизительно 3,5 пикселя по уровню половины высоты пика. В экспериментах, для которых разрабатывались новые методы обработки данных, чаще всего приходится иметь дело с пиками, для которых параметр σ равен 1…2 пикселя.

Во-вторых, использовался “деформированный” пик (рис.2б), который моделировался сложением трёх гауссовских пиков с различными параметрами.

При анализе чувствительности методов обработки данных к шуму на брэгговский сигнал накладывался шум с гауссовским спектром. Если уровень шума не оговорён особо, то среднеквадратическое значение шума составляло 0,5% от амплитуды пика.

В дальнейшем под ошибкой определения положения пика понимается разность между вычисленным положением пика и его действительным значением, а термин ширина полосы ошибки используется для обозначения разности между максимальным и минимальным значением ошибки, то есть как характеристика ошибки в смысле “от пика до пика”.

Ширина полосы ошибки является удобной величиной для характеристики ошибок метода и именно эта величина будет исполь- зована при оценке результатов расчёта по тому или иному методу в случае незашум-лённого модельного спектра.

В том случае, когда модельный спектр зашумлен, в выходных данных также появляется шумовая составляющая. Если эта шумовая составляющая существенно превышает ошибку метода, для количественной характеристики ошибки оказывается более удобным использовать среднеквадратическое значение шума в выходном сигнале, а не ширину полосы ошибки “от пика до пика”.

Для участия в процедурах аппроксимации и для расчётов по центроид-методу выбирались те точки брэгговского пика, которые лежат в интервале от 10 до 100% его полной высоты (так называемые основные точки ). Кроме того, к этим точкам могло быть добавлено по несколько точек слева и справа от основных, то есть точек на “крыльях” пика. В дальнейшем для таких точек будет использоваться термин дополнительные точки .

Результаты моделирования для центроид-метода

Сначала рассмотрим результаты применения центроид-метода к брэгговскому пику гауссовской формы (рис.2а). Если в дальнейшем не оговорено особо, параметр σ (дисперсия гауссовского распределения) был выбран равным 1,5 пикселя, что приблизительно соответствует параметрам пиков, наблюдав-

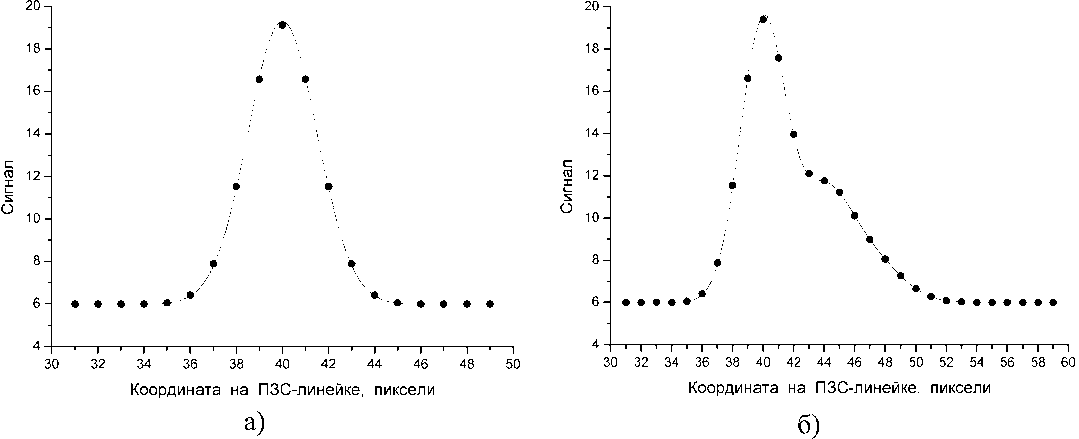
Рис.2. Примеры модельных брэгговских пиков: а ě гауссовский, б ‒ “деформированный”. линия ‒ зависимость освещенности ПЗС-линейки от координаты, точки ‒ значения сигнала, получаемого с ПЗС-линейки

шихся в экспериментах. В последствии (при сравнении результатов моделирования для центроид-метода и метода с гауссовской аппроксимацией) использовались значения σ в диапазоне 0,5…7,5 пикселя.

Хотя при отсутствии дополнительных точек центроид-методу свойственны достаточно большие ошибки, ошибки центроид-метода имеют свойство резко снижаться при увеличении числа дополнительных точек. Так, если при отсутствии дополнительных точек была получена ширина полосы ошибки приблизительно 0,05 пикселя, то уже при использовании по одной дополнительной точке с каждой стороны пика ширина полосы ошибки снижается приблизительно до 0,008 пикселя, при трёх точках ‒ до 6 ⋅ 10 ^{- 6} пикселя, при пяти точках ‒ до 7 ⋅ 10 ^{- 8} пикселя.

В случае “деформированного” (негауссовского) брэгговского пика ситуация ухудшается непринципиально ‒ тот факт, что “крылья” такого пика спадают медленнее, приводит лишь к необходимости включать в расчёт большее число дополнительных точек, что не вызывает вычислительных трудностей вследствие простоты центроид-метода.

Таким образом, при отсутствии шума центроид-метод даёт прекрасные результаты и если бы не влияние шума, то другие методы обработки данных вряд ли бы представляли практический интерес. Однако, реальный сигнал всегда в той или иной мере зашумлён, а к шуму центроид-метод оказывается весьма чувствительным.

Так, например, в случае гауссовского пика наличие гауссовского входного шума со среднеквадратическим значением 0,5% от амплитуды пика приводит к появлению заметного шума в выходном сигнале. При одной дополнительной точке с каждой стороны пика среднеквадратическое значение выходного шума составляет около 0,013 пикселя, при трёх дополнительных точках ‒ около 0,021 пикселя, а при пяти дополнительных точках ‒ около 0,03 пикселя.

Значения шума 0,013...0,03 пикселя следует считать достаточно большими ‒ как будет показано в следующем разделе, метод гауссовской аппроксимации брэгговских пиков обеспечивает меньший выходной шум. Кроме того, неприятной особенностью центроид-метода является рост выходного шума при увеличении числа дополнительных точек. Это означает, что попытка гарантировано уменьшить ошибку центроид-метода путём использования большого числа дополнительных точек при обработке данных реального эксперимента неизбежно приведёт к возрастанию шумовой составляющей ошибки. Поэтому, если центроид-метод всё же используется для обработки экспериментальных данных, количество дополнительных точек должно выбираться из компромиссных соображений.

Зависимость выходного шума центроид-метода от ширины гауссовского брэгговского пика представлена на рис.3б (кривые C-5 и C-15).

Для негауссовского пика (рис.2б) ошибка центроид-метода также снижается по мере увеличения числа включаемых в расчёт точек, хотя это снижение происходит несколько медленнее ‒ из-за того, что показанный на рис.2б пик имеет более широкие “крылья”. Среднеквадратическое значение выходного шума при трёх дополнительных точках составляет около 0,022 пикселя.

Результаты моделирования для метода определения положения брэгговских пиков с использованием гауссовской аппроксимации

Как уже отмечалось во введении, большую важность представляет вопрос об исследовании ошибок метода. Численное моделирование показывает, что для всех исследованных методов при обработке данных об узких (σ ≤ 0,5 пикселя) брэгговских пиках наблюдается возрастание ширины полосы ошибки до недопустимо больших значений. При этом центроид-метод обеспечивает приемлемую для практических целей ширину полосы ошибки (порядка 10-3 пикселя и менее) при значениях параметра σ ≈ 0,6...0,7 пикселя и более. Предлагаемый метод определения положения брэгговских пиков с помощью гауссовской аппроксимации обеспечивает прием- лимую для практических целей ширину полосы ошибки при значениях параметра σ ≈ 0,7...0,8 пикселя и более (рис.3а). Таким образом, обусловленные ошибками метода ограничения на применение нового метода обработки данных оказываются практически такими же, как и у центроид-метода.

В то же время предлагаемый метод оказывается существенно более устойчив к шуму во входном сигнале, чем центроид-метод (рис.3б). Это преимущество особенно выражено в случае обработки данных об узких брэгговских пиках.

Кроме того, в отличие от центроид-метода, выходной шум предлагаемого метода практически не зависит от числа участвующих в расчётах дополнительных точек. Этот факт существенно упрощает выбор необходимого числа точек ‒ допустимо выбирать это число с заведомым завышением, не опасаясь увеличения выходного шума.

При обработке данных о негауссовских брэгговских пиках прежде всего представляет интерес вопрос о том, можно ли вообще определять положение такого пика с помощью гауссовской аппроксимации. Здесь необходимо отметить, что при решении такой задачи интерес представляет не вопрос о том, насколько велика или мала оказывается величина Q в формуле (2), а вопрос о том, насколько адекватно смещение максимума аппроксимирующей кривой следует за смещением брэгговского пика вдоль линейки светочувствительных пикселей. И, поскольку интерес представляет не столько абсолютное значение положения пика, сколько изменение этого положения при том или ином воздействии на брэгговский датчик, метод обработки данных можно считать отвечающим практическим потребностям, если величина смещения максимума аппроксимирующей функции всегда оказывается равной смещению брэгговского пика.

Численное моделирование для негауссовского пика, изображённого на рис.2б, а также для ряда других негауссовских пиков показало, что во всех исследованных случаях требуемая адекватность обеспечивалась ‒ при достаточном числе дополнительных точек ошибку метода удавалось уменьшить до любого реально необходимого значения.

Устойчивость предлагаемого метода к входному шуму в случае негауссовских пиков также оказывается выше, чем у центроид-метода. Однако, выигрыш не столь существенен, как в случае гауссовских пиков ‒ так,

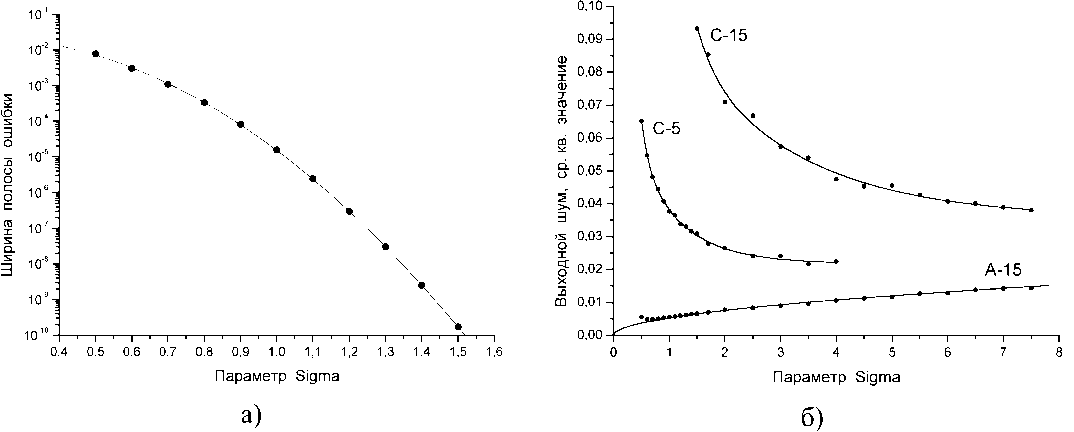
Рис.3. Зависимости: а ‒ ширины полосы ошибки метода определения положения брэгговских пиков с использованием гауссовской аппроксимации от параметра σ (дисперсии гауссо вско го распределения) брэгговского пика, б ‒ выходного шума от параметра σ брэгговского пика.

Кривые C-5 и C-15 ‒ для центроид-метода при 5 и 15 дополнительных точках с каждой стороны пика, кривая A-15 ‒ для метода определения положения брэгговских пиков с использованием гауссовской аппроксимации. Кривая A-15 представляет собой кривую типа y ~ x . Во всех случаях моделирование проводилось для пика гауссовской формы. По всем осям использованы безразмерные единицы (пиксели)

например, для показанного на рис.2б брэгговского пика среднеквадратическое значение выходного шума уменьшается приблизительно в 1,5 раза.

Некоторые предварительные выводы

Итак, проведённое моделирование показывает, что центроид-метод можно рекомендовать к использованию в том случае, когда брэгговский спектр отличается высоким отношением сигнал/шум. Этот метод может представлять интерес также и в том случае, когда требуется повышенная скорость вычислений ‒ в этом случае данный метод может оказаться наиболее преемлимым с точки зрения снижения объёма производимых “в реальном времени” вычислений.

Метод определения смещения брэгговских пиков с помощью гауссовской аппроксимации обладает повышенной (по сравнению с центроид-методом) устойчивостью к входному шуму и независимостью уровня выходного шума от числа участвующих в расчёте точек. Этот метод пригоден для обработки данных и в случае негауссовских пиков.

Но, в то же время нельзя не отметить и серьёзный недостаток метода определения смещения брэгговских пиков с помощью гауссовской аппроксимации, требующей проведения нескольких итераций ‒ очень большие затраты машинного времени на его реализацию. Как следствие этот метод оказывается практически неприменим в том случае, когда требуется анализ быстропротекающих процессов “в реальном времени”. В случае же анализа относительно медленных процессов или же в случае сохранения данных о бы-стропротекающем процессе и анализа этих данных после завершения эксперимента такой метод может оказаться весьма полезен.

Однако, пока рано делать окончательные выводы о том, какой метод анализа брэгговских спектров следует выбирать в том или ином конкретном случае ‒ такие выводы будет целесообразно делать после рассмотрения корреляционных методов определения смещения брэгговских пиков, которые будут представлены работе [2].