Метод интегральных преобразований в решении задачи обнаружения малогабаритных транспортных средств на изображениях

DOI:

Научный центр безопасности дорожного движения при Министерстве внутренних дел Российской Федерации провел очередной информационно-аналитический обзор дорожно-транспортной аварийности в РФ за шесть месяцев 2023 г. . В своем отчете ведомство привело статистику по аварийности, которая связана с популярными на сегодняшний день средствами индивидуальной мобильности, такими как электрические самокаты и велосипеды.

За первое полугодие 2023 г. зарегистрировано 2 151 (+8,6 %) ДТП с пострадавшими велосипедистами, в которых погибли 89 (-29,4 %) и получили ранение 2 072 (+11 %) велосипедиста. Доля таких происшествий среди всех ДТП составила 3,8 %, что выше, чем в первом полугодии 2022 г. (3,7 %). Тяжесть последствий данных ДТП составила 4,1.

Нужно отметить, что велосипедист на проезжей части не редко представляет собой мало заметный объект, к тому же движущийся намного медленнее, чем движется поток машин. Следовательно, было бы весьма полезно иметь некоторое дополнительное устройство, предназначенное для отслеживания таких малогабаритных участников движения. В первую очередь для такого устройства потребуется соответствующее программное обеспечение. Следует сразу уточнить, что данное программное обеспечение должно работать почти в режиме реального времени, что накладывает на него определенные требования по скорости обработки видеокадров.

В настоящей работе мы предлагаем собственный подход к решению поставленной задачи. Именно, определяем набор специальных признаков на изображении, вычисление которых основано на ряде интегральных операторов, а также разрабатываем метод обработки полученных признаков с помощью некоторых преобразований меток обучающего набора изображений.

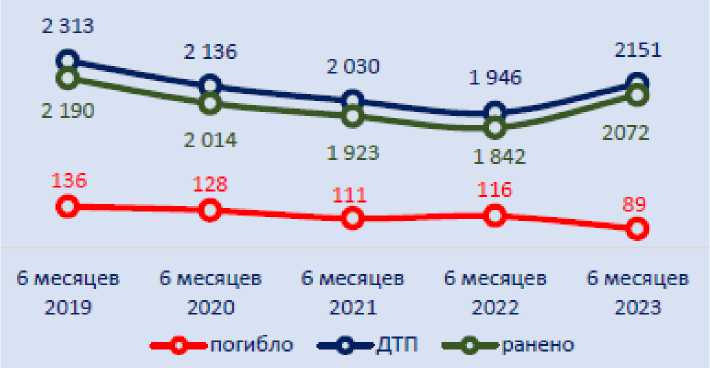
Рис. 1. Показатели аварийности с пострадавшими велосипедистами

1.    Общая идея метода

В задачах компьютерного зрения чаще всего используют два подхода. Первый основан на заранее известной информации об объектах, которые изображены на снимках: это может быть их форма (используется контурный анализ), цветовой тон (используются различные методы цветовой фильтрации) и т. д. В этом случае для выделения и распознавания объектов применяются базовые алгоритмы обработки изображений [5]. Другой подход основан на применении методов машинного обучения, что предполагает выделение некоторых признаков, характеризующих изображенные объекты (см., например, [2; 6–8; 13; 15; 17; 18; 21]. Процесс обучения на достаточно большом наборе входных изображений позволяет определить наиболее характерные признаки, присутствующие в данном наборе. В следующих работах можно познакомиться как с задачами, решаемыми при помощи сверточных нейронных сетей, так и с их архитектурой [1; 3; 4; 12; 14; 16; 19; 20]. К примеру, в статье [10] инструмент нейронных сетей использовался в задаче пространственной реконструкции объектов на основе ряда его изображений. Нами в работе представлен иной подход вычисления признаков, основанный на различных интегральных преобразованиях. В частности, мы применяем идеи, опирающиеся на три интегральных преобразования: преобразование Радона [22], функции Стеклова [11] и дискретное преобразование Фурье [5].

Наш подход предполагает вычисление ряда числовых признаков для изображения с помощью определенных интегральных преобразований.

Для произвольной функции z = f (х,у) , определенной на плоскости (х, у) , полагаем

+ ∞

R(r, ф) = У f (г cos ф + t sin ф,г sin ф — t cos ф}И, -∞ где г > 0 и ф Е [0, 2п). Полученная функция R(r, ф) есть интеграл по всем прямым плоскости, которые описываются уравнениями х = г cos ф + t sin ф, у = г sin ф — t cos ф, t Е (-ж, +ж).

Полученная функция R(r, ф) называется преобразованием Радона функции f (х,у). Нужно отметить, что при определенных условиях на функцию f (х,у) она однозначно восстанавливается по ее преобразованию Радона. Если f (х,у) задает яркость точки (х,у) на изображении, то вместо интегралов по всем прямым будем рассматривать среднюю яркость по всем вертикальным, горизонтальным и диагональным линиям, то есть вычислять среднюю яркость по строкам, столбцам и диагоналям изображения. При этом подходе мы теряем часть информации. Однако, это вполне допустимо, так как при решении задач классификации изображений нет необходимости их полного восстановления.

Помимо преобразования Радона мы будем использовать оператор осреднения Стеклова В.А. (функции Стеклова). Для заданной функции z = f(х,у) и h > 0 по- лагают

x + h/ 2 y + h/ 2 f h (x,y) = — J j f(u,v)dvdu. x - h/ 2 y - h/ 2

Таким образом, f _h (x,y) есть среднее значение функции f (х,у) в квадрате [х — h, ,х + + h ] х [у — h ,у — h ] . Известно, что для непрерывной функции f(х,у) семейство функций f _h (x,y) равномерно сходится к исходной функции на компактных множествах при h ^ 0 . Для случая изображений мы заменим интегралы на суммы и результат такого преобразования будем рассматривать в отдельных точках. В итоге получим следующую конструкцию. Разбиваем входное изображение на блоки пикселов и в каждом блоке вычислим среднее значение яркости. Полученный набор значений записываем в отдельный массив. Здесь также происходит потеря информации и восстановить по этим данным изображение невозможно. Однако эти потери вполне допустимы при решении задач распознавания объектов на изображении, что будет показано в следующих разделах статьи.

Любое изображение размера Nc х Nr в оттенках серого цвета можно считать функцией двух переменных f (х,у) как функцию яркости точки (х,у), где х — номер столбца и у — номер строки. Введем обозначения sy(х) = j r

Nr

Nc

• 12^{f ( х,}у), ^S X⁽ у) = w •     ^{f ( х,}у).

^{N С}

У =0

Дугими словами, S y (х) — средняя яркость пикселов изображения f , расположенных в столбце х , S ^y (у) — средняя яркость пикселов изображения f , расположенных в строке у . Помимо этого, рассмотрим средние яркости, вычисленные по диагональным направлениям. Предположим, что N _r = N _c (в алгоритме мы все изображения приводим к квадратному виду). Пусть

1 У                                  1       N_r - 1

D ^{y (}у) =      • ^f ⁽ у ^— х,х\ D ^{y (} у) = —--^^{f (N} r ^— 1 + у ^— х^,х ⁾ ,  (2)

у+ 1 Х=0                    Nr— у где у = 0,1, 2,...,Nr — 1. Функции Dy1_ (у) и D, (у) представляют собой средние значения яркостей точек, расположенных по диагоналям. Для вычисления средних значений яркости точек, расположенных на диагоналях другого направления, достаточно транспонировать матрицу изображения и воспользоваться формулами (2).

С определенной точностью введенные величины Sy(х), SX(у), Dy(у) и Dy(у) аппроксимируют (суммирование ведется только по вертикальным, горизонтальным и диагональным прямым) преобразование Радона изображения f. Поэтому, можно попытаться использовать их в задачах классификации изображений. Исходное изображение мы разбиваем на 4 равные части и данные вычисления выполняем для каждого из них. В итоге получаем, что количество признаков К = 4Nr + 3Nr.

Как уже было сказано, помимо преобразования Радона мы используем функции Стеклова. Для случая изображений определим их так. Зададим натуральное число q = = 2к + 1 , к = 0,1, 2,... , и для каждой точки (х,у) , х = к, к + q,..., k + [N _r /q]q — q, у = = к, к + q, ...к + [N _r /q]q — q , положим

1 к к

^A q ^{( Х,}У)= 2£ ^ ^{+ ( Х +} КУ + V).

^q и = - ки = — к

Данная величина определяет осредненное изображение. При этом A _q (х,у) = f (х,у) когда q = 1 ( к = 0 ). На рисунке 2 можно видеть результат такого преобразования. Заметим, что общие очертания изображенного велосипедиста легко угадываются, что дает возможность использования полученных признаков в задачах классификации.

Рис. 2. Исходное изображение и изображение признаков S _q( х,у )

Добавив эти значения, получим уже К = 7N _r +

( ^ ) ²

признаков.

На рисунке 3 видим результат этих преобразований. После этого изображение разбивается на блоки размера q х q. В каждом таком блоке формируется набор светлых точек в виде массива, содержащего пару [х{,у{], где у^ — номер строки и Х{ — номер столбца г-ой светлой точки. Затем этот набор точек аппроксимируется прямолинейным отрезком, который описывается уравнением у = а • х + Ь. Параметры а, b вычисляются методом наименьших квадратов a =

г             гг г^х* - Erf • Е vi i=1________i=1i гг r E J - E xi)

i=i       \i=i/

ь =¹ r

t *

\ i=1

— a •

t ^, i =1   /

где r — количество светлых точек в блоке.

Данные величины могут служить признаком на изображении, так как эти отрезки приближают набор белых точек в блоке (рис. 4). Получаем К = 7Nr + 3

( 7 ) ²

Рис. 4. Аппроксимация набора светлых точек прямолинейным отрезком

И, наконец, дополним вычисленные признаки коэффициентами дискретного преобразования Фурье, используя как действительную, так и мнимую части

1     N_c ^{— 1} N_r -¹               (        /              Л

F (u,v) =

E E /(rfV)e^xP — ~Пт    + *—\ ,

N г N _c J0₀ JJ       1     \N _C   NJ J

Рис. 5. Исходная картинка и результат применения преобразования Фурье (8 х 8 коэффициентов)

При этом мы оставим только / 2 (I х I) комплексных коэффициента, находящихся в левом верхнем углу (для 0 <  и < I и 0 <  и < / ). В итоге для изображения будет сформирован набор из

К = 7N _r + 3 ( ^{N r} ) + 2/ 2

числовых признаков, которые в дальнейшем будем использовать для решения задачи классификации. Далее опишем собственный подход к построению классификатора на основе метода наименьших квадратов.

2.    Описание метода наименьших квадратов

Рассмотрим некоторое отображение f : R ⁿ ч R ^m , п , т >  0 , значения которого известны в конечном множестве точек X С R ⁿ

f(х _г )= _{V i} , г = 1,...,N, N = | X | .

Метод наименьших квадратов решает задачу поиска наилучшего линейного приближения отображения f в смысле минимизации величины

N

L(A) = ^ lAxi - yi |2 ч min, i=1

где минимум берется по всем матрицам A Е М _т,_п размерности т х п . Задача поиска этого минимума сводится к решению уравнения

• V L(A) = 0.

Здесь градиент считается в пространстве М _т,_п со скалярным произведением

{ A, В ) = trA ^T B.

Представим множество X матрицей X Е М _{N п} , а множество значений Y матрицей Y Е M _N,_m , располагая в строках координаты соответствующих точек

X _ij = x ^j А = 1,..., N, j = 1, ...,п.

Y ij = y ^j ,г = 1, ...,N, j = 1, ...,m.

Градиент функции L(A) вычисляется исходя из формулы dL(H) = (УL(A\ Н) V H Е Мт,п.

N dL(H) = 2 £(Ax, - yi, Hx^ = i=1

N

= 2 ^(Axi ® Xi - yi ® Xi, H) = i=1

= 2 ( A • X ^T • X - Y ^T • X, H Y