Метод интегральных уравнений для векторной обратной задачи

• I.    Постановка задачи

Пусть A(t) =|| aij(t) || - квадратная матрица n-го порядка, f (t) =|| fi(t) Ц^, x(t) =|| xi(t) ||n=1

У ( t ) = || y j ( t ) || m = 1 — векторные функции.

Рассмотрим динамическую систему, описываемую системой обыкновенных линейных дифференциальных уравнений n -го порядка:

x (t) + A(t) x (t) = f (t)(1)

В дальнейшем будем предполагать, что коэффициенты системы и её правые части определены и непрерывны на некотором промежутке [ a; b ].

Пусть далее T = || t ij || - постоянная матрица формата m х n , m >  1 и

У(t) = T • x(t) .(2)

Матрицу T будем называть матрицей косвенных измерений.

Требуется, располагая косвенными измерениями (2), определить входное воздействие f ( t ) .

• II.    Согласованность измерений. Однозначная разрешимость задачи

Обозначим через t^j = || t j 1 , t j ₂ ,..., t jn ||, j = 1,2,..., m строки матрицы T . Если ранг матрицы T равен r , то можно выбрать ровно r линейно независимых строк этой матрицы и выразить m - r оставшихся через них. Другими словами, существует постоянная матрица Л формата ( m - r ) х r такая, что

Здесь для определенности мы положили линейно независимыми первые г строк. При этом, в случае совместности системы косвенных измерений (2) измеренные в эксперименте функции y ( t ) = 11 y j ( t ) II " = 1 должны быть связаны соотношениями:

У г + 1

У г + 2

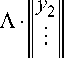
yr

ym которые мы называем условиями согласованности измерений.

Отсюда заключаем, что справедливо следующее утверждение.

Лемма. Система косвенных измерений (2) совместна тогда и только тогда, когда наблюденные в эксперименте функции y j (t ), j = 1,2,..., m удовлетворяют условию (3).

Если при этом г = n <  m - система (2) имеет единственное решение, если же г <  n - бесконечное множество решений.

Простые рассуждения позволяют установить справедливость теоремы.

Теорема. У задачи нахождения правой части f ( t ) системы (1), отвечающей косвенным измерениям (2) существует единственное решение тогда и только тогда, когда наблюдения дифференцируемы, ранг матрицы косвенных измерений равен размерности задачи (г = n) и выполнено условие согласованности измерений (3).

Если условие (3) не выполнено – решений нет, если выполнено и ранг матрицы косвенных измерений меньше размерности задачи – решений бесконечно много.

• III.    Регуляризация косвенных измерений

Как правило, в прикладных исследованиях условия сформулированной выше теоремы не выполняются и в этом случае с теоретической точки зрения поставленная задача восстановления входного сигнала решений не имеет либо таковых бесконечно много. Связано это обстоятельство с погрешностями, присущими всякому измерительному процессу. В этой ситуации на практике прибегают к некоторой модификации системы косвенных измерений (2) с целью добиться выполнения условий (3) и однозначности обращения системы (2). Достигается это за счет привлечения некоторой дополнительной информации о решениях системы (1) и/или за счет расширенного понимания процедуры обращения линейной системы (2).

Использование дополнительной априорной информации о системе - вопрос отдельного исследования, и его изучению посвящено множество работ (например, [1-3] и цитированная там литература).

Мы же остановимся здесь на расширении трактовки термина решение системы линейных уравнений, понимая под последним нормальное псевдорешение [4].

Напомним, что нормальным псевдорешением системы линейных уравнений y = Tx называется вектор хнорм, такой, что xнорм   arg minx=argmin||y—Tx|| || x ||.

Известно [4], что нормальное псевдорешение всегда существует и единственно. Оно представимо в виде х_норм = T ⁺ y, где T ⁺ - матрица, псевдообратная [4] к матрице T .

Очевидно, что если у системы существует, по крайней мере, одно обычное решение, то невязка для него равна нулю и нормальным решением будет обычное решение с наименьшей нормой. Если же система однозначно разрешима, то нормальное псевдорешение совпадает с обычным.

Везде в дальнейшем под решением системы косвенных измерений (2) мы будем понимать её нормальное псевдорешение.

Пример. В приложениях (в частности, в теории динамических измерений [5]) часто встречается ситуация, когда матрица T = || t 11 ,t ₁₂ ,..., t 1 _n || - матрица-строка. В этом случае псевдообратная

^T + T матрица имеет вид:   T =---- , а нормальное псевдорешение дается соотношением

E tv

У ( t )

хном =     T , где y(t) - единственная скалярная компонента измеряемого сигнала, T - р         /2

Z tli столбец элементов матрицы T .

• IV.    Точность косвенных измерений

Как уже было отмечено выше, как правило, в прикладных ситуациях измерения сопровождаются различными погрешностями, так что фактически исследователь имеет дело не с системой (2), а с возмущенной системой у (t) = У (t) + Аy (t) = Tx(t) .                                       (4)

Пусть х норм ( t ) - нормальное псевдорешение невозмущенной системы y(t ) = Tx(t ) , х НОрм ( t) – нормальное псевдорешение возмущенной системы (4). Интерес представляет ответ на вопрос, насколько возмущения A _y ( t ) измеряемого сигнала y ( t ) влияют на погрешность А _х ( t ) нормального псевдорешения. Оценивая упомянутую погрешность по норме пространства L n ^j, получаем:

II А х || = || Х норм - Х нОМ | Н T ⁺ y - T ⁺ y | Н | T ⁺ ( y - y ) | й | T ⁺ || - || А , ||.

Здесь 11 T ⁺ 11 - норма оператора псевдообращения. Если 1| А _y 11 < 5 , то 1| А _х 11 < 11 T ⁺ 11 -5 . Так, например, для важного в приложениях случая матрицы-строки получаем:

T = || t _h ||,  || T ⁺ || = — =   . ¹      ^   || А_х || <   , ⁵    .

• ^{1 i                                                                   Х}

°^{T ||}   VE tv             Z t l t 2

Более точные оценки можно найти, например, в [4].

Здесь важно отметить еще одну особенность задачи с возмущенными косвенными измерениями - погрешности измерений А _y могут быть сколь угодно «плохими» с аналитической точки зрения, например недифференцируемыми и даже разрывными. А потому получить правую часть уравнения (1) простой подстановкой нормального псевдорешения не удается.

• V. Основные расчетные соотношения

Хорошо известно (например, [6]), что задача Коши ^{х (} t ) ^{+ A(} t ) х^(t ) = f ⁽ t ), ^{х (} t о ) = ^х 0

начальных усло-

с непрерывными коэффициентами A(t ), f (t ) однозначно разрешима для любых вий х ₀ и её решение дается интегральным соотношением

х(t) = Ф(t)хо + Ф(Г) J Ф-1 (5) f (5)ds , tо где Ф(t) - фундаментальная матрица системы (5), удовлетворяющая уравнению d Ф( t) + A( t )Ф( t) = 0 < dt                            ,

Ф ( t о ) = I которое эквивалентно интегральному соотношению

Ф ( t ) + J A ( s ) Ф ( s ) ds = I .

t 0

Заметим, что соотношение (8) представляет собой систему интегральных уравнений Вольтерры второго рода относительно компонент фундаментальной матрицы Ф ( t ).

Умножая обе части соотношения (6) на матрицу Ф ^{- 1}( t ) и обозначая u(t ) = Ф ^-1^ ) х ( t ) - х ₀ , перепишем (6) в виде:

t

{ ф ^{- 1}( 5 ) f (s ) ds = u(t) ,                                       (9)

t 0

отмечая, что в этом случае полученное соотношение – интегральное уравнение Вольтерры первого рода относительно функции f (t) .

Пусть y(t ) = y(t ) + A _y (t ) - косвенные экспериментальные измерения, х Норм ( t ) - соответствующее нормальное псевдорешение системы y(t ) = Tx(t ) .

План решения основной задачи выглядит так:

• •    построение нормального псевдорешения х ^орм (t ) системы косвенных измерений;

• •    решение уравнения (8) с целью нахождения фундаментальной матрицы Ф ( t );

• •    решение уравнения (9)

t

J o ^{- 1}( s ) f ( s ) ds = u ( t) = Ф ^{- 1}( t) х норм ( t ) - х вом ( t o ) t 0

с целью нахождения функции f ( t ), которая и считается приближенным вариантом отыскиваемой правой части системы (1).

Отметим, что результат решения уравнений (7) – (8) от точности измерений и процедуры обращения системы (2) не зависит. Кроме того, вычислительные процедуры решения уравнения второго рода устойчивы относительно погрешностей вычисления (например, [7–8]). Поэтому нахождение фундаментальной матрицы системы (1) особых затруднений не вызывает¹.

Иначе обстоит дело с решением интегрального уравнения (9) с неточно заданной правой частью. Как уже было отмечено выше, погрешности косвенных измерений вызывают погрешности при нахождении нормального псевдорешения, которые могут оказаться значительными. Кроме того, численные процедуры решения уравнений второго рода неустойчивы и это тоже может привести к заметному искажению результата.

Процедура решения уравнения (9) с неточно заданной правой частью требует регуляризации [7–9] и последующего анализа точности получаемого таким способом решения.

• VI.    Регуляризация

Напомним (например, [7–9]), что регуляризирующим оператором для уравнения Af = u , f g F , u e V называется отображение R :{(U , 5 )| U e V , 5 >  0} ^ F , удовлетворяющее условию V f e F , V u g V таких, что Af = u , p _V ( u, u ) <  5 , должно выполняться f = R(u , 5 ) ^ f , если только 5 ^ 0. Если задача регуляризуема, то её решением называется результат применения регуляризующего оператора к исходным данным.

Пусть оператор A: F ^ V линеен и ограничен, и нам известны A:  || A - A ||< е и u:  || u - u | |U < 5. Для построения приближённого решения f , сходящегося к точному решению f при стремлении δ и ε к нулю, широко применяется следующий регуляризирующий алгоритм [7, 9].

Рассмотрим M ^а [ f ] - функционал, задаваемый соотношением

M ^а [ f ] = | Af - u || V + a .Q [ f ],                            (10)

где Q|f ] =|| f |F . Пусть fa - элемент, доставляющий минимум функционалу Ma[f ] на F . Если параметр регуляризации a = a(^,^) удовлетворяет определенным условиям (подробнее, напри- мер в [7-9]), то элемент fa будет приближённым решением рассматриваемого уравнения.

В нашем случае оператор A дается соотношением (9), а стабилизатор Q был выбран в виде

t

n

ЭД ^{f ]} = 1 Z Pi⁽ s ) ft ²⁽ s ) ds ’ Pi ⁽ s ) ^- °’ s ^{e [} a ; b ^] • t ° ^{( 1}                   ^

Полагая f = || f i ||, Ф ^{- 1}( s ) = || g ij ( s ) ||, i , j = 1,2,..., n , перепишем (10) в скалярной форме

M ^a [ f ] = 1

t °

т

A 2

Z ui ^{( т )} — fZ g ij ⁽ s ) f j ⁽ s ) ds + ^a Z P k ^{( т )} Л ^{2( т ) d T ,} i                  tj                                        k

сводя таким образом задачу решения интегрального уравнения (9) к задаче минимизации функционала (11).

• VII.    Оценивание точности

Существует несколько способов оценивания точности решения уравнений, подобных рассматриваемому нами. Пример априорной оценки точности можно найти в [10], алгоритм получения апостериорной оценки подробно рассмотрен в [11].

Мы ограничимся эмпирической оценкой, дающей оценку снизу для наихудших значений вычислительной точности алгоритма AC и точности метода регуляризации Ar . Для их нахождения решим две модельные задачи.

Зададим гладкую вектор-функцию x и по уравнению (1) вычислим f_Mод = x + Ax , получив точное решение невозмущённого уравнения (9). Соответствующую ему правую часть и_мод вычислим, используя нормальное псевдорешение системы (2) х_норм = T ⁺ y = T ⁺ Tx . Таким образом, мы построили задачу решения уравнения (9) с невозмущёнными исходными данными и известным точным решением. Если f_Mod - решение построенной модельной задачи, полученное методом регуляризации, то наихудшая вычислительная точность алгоритма оценивается как

||^fмод    ^f мод ||

^A C^    ||fмоА   ■

Далее рассмотрим модельную задачу с возмущёнными исходными данными для оценки точности A R метода регуляризации. Как и выше, вычислим точное решение f _мод по заданной гладкой вектор-функции x . Вычислим вектор наблюдений y = Tx , возмутим его, положив

Увозм (t) = y(t) + ^), где ^(t) — функция погрешности. Далее найдём возмущённое нормальное псевдорешение системы (2) x^pM = T+Увозм и вычислим возмущённую правую часть иО" уравнения (9). Если fвозМ - регуляризованное решение уравнения (9) с возмущённой правой частью, возм то наихудшая точность регуляризирующего алгоритма оценивается как AR ^  "о.-—м-—-.

f мод

• VIII.    Численная реализация. Пример

В качестве примера была рассмотрена динамическая система

Г x ⁽ t ) + A ⁽ t ) х (t ) = ^{f (} t )’

[y(t) = Tx(t), t° < t < h второго порядка со следующими модельными параметрами:

( 13)    , х      <5cos2t t° = °, h = 3, A =         |, T = (2 3), x(t) = |    .

(- 1  1 )                   ^ 3sin3 t

t

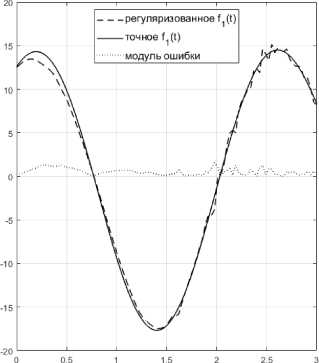
Дискретизацию задачи решения уравнения ^Ф (s) f (s)ds = u (t) проведём на равномерных сетках {tk = k • h ,k = 0, N} для t us с N = 100. Параметр регуляризации выберем эмпирически (можно при выборе также пользоваться обобщённым принципом невязки, описанным в [9]), руководствуясь минимальностью относительной ошибки регуляризованного решения. На рис. 1 показано точное решение fмод и вычисленное приближённое решение fмод. Относительная точ ность регуляризованного решения составила 51 f = 0,375.

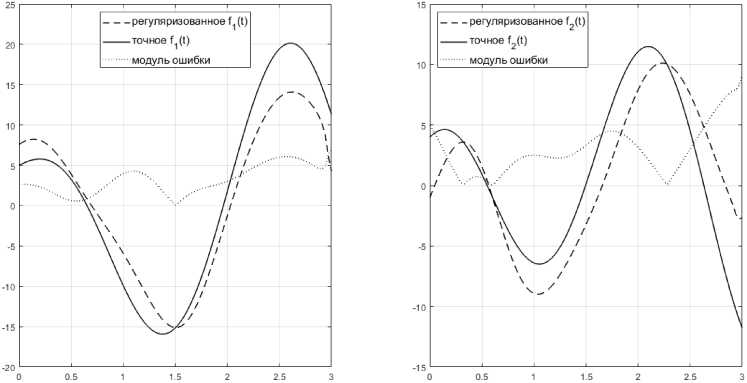
Рис. 1. Решение точной модельной задачи

Для построения возмущенной модельной задачи наложим на наблюдения y аддитивную нормально распределённую помеху с нулевым средним так, чтобы возмущённое yвозм имело относительную ошибку 0,01. Решение fмвоодзм возмущённой модельной задачи изображено на рис. 2.

Относительная точность составила 5 2 f = 0,377.

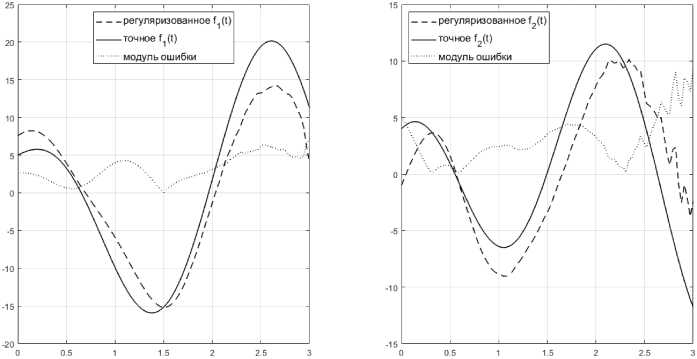
Рис. 2. Решение возмущённой модельной задачи

Видно, что относительная точность решения искаженной модельной задачи почти не изменилась по сравнению с точной модельной задачей. Заметим, что при этом величины 5 1 f и 5 2 f относительно вел и ки. Это связано с тем, что решением интегрального уравнения (9) является вектор-функция f н , которая вычисляется не по вектору x , задаваемому нами в модельной задаче, а по нормальному решению х_НО р _М , ^{то есть f} норм = х_Н ор _М + Ax_HO p _M .

Эти соображения подтверждаются численным экспериментом. На рис. 3 изображено решение f_норм точной модельной задачи в сравнении с f_норм . Относительная точность ⁵ 1 f орм = ^0,002.

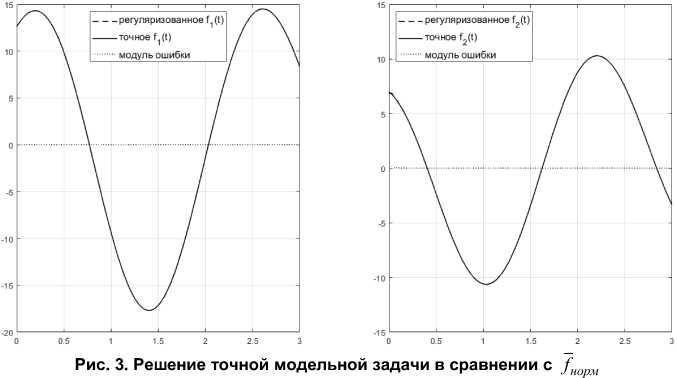
Для сравнения решим ту же искажённую модельную задачу и сравним её решение с f_норм . На рис. 4 изображено приближённое решение f_н^в_о^о_р^з_м^м и f_норм . Относительная точность решения 5 2 f орм = 0,101.

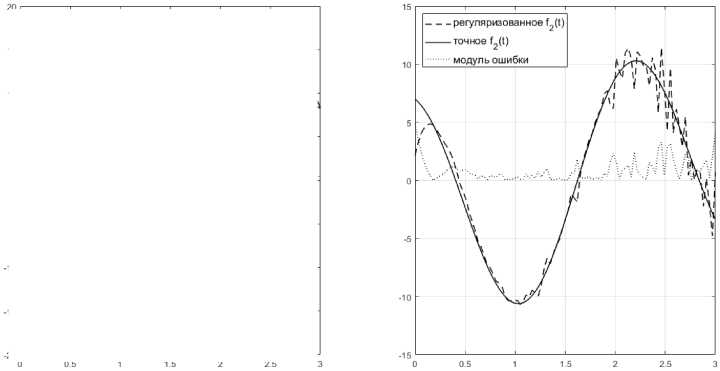
Рис. 4. Решение искажённой модельной задачи в сравнении с f _норм

Таким образом, наблюдается неустранимая ошибка решения, связанная с разницей между x и нормальным псевдорешением x_норм системы измерений (2). Очевидно, что в случае, если система измерений имеет единственное обычное решение, регуляризованное решение задачи (1)–(2) ведёт себя аналогично изображённому на рис. 4 приближённому решению.