Метод эмпирических ортогональных функций в задаче восстановления общего содержания CO2 по данным спутникового Фурье-спектрометра GOSAT

Исследования климата Земли включают множество задач, которые связаны с изучением его изменчивости, исследования причин и взаимосвязи наблюдаемых изменений в зависимости от различных факторов (естественных или антропогенных). Важной задачей является получение количественных оценок факторов, определяющих изменения климата и связанных с ними других изменений, например, определение источников и стоков парниковых газов, поиск временных циклов газовых компонент атмосферы, определение формирования и пространственновременного распределения аэрозолей и др. Решение обозначенных выше задач позволит уменьшить неопределенность в оценке прогноза изменений климата, уточнить модельное описание состояния атмосферы и климатической системы в целом.

Значимым фактором, влияющим на изменения климата Земли, является углекислый газ, знание пространственно-временного распределения (ПВР) которого важно для решения раз- личных задач. Для построения и изучения ПВР СО2 необходимо иметь множество измерений, причем на равномерной пространственной и временной сетке. Имеющиеся источники информации о содержании СО2 в атмосфере [8–10] являются неравномерно распределенными по поверхности Земли, не все имеют регулярные по времени измерения, обладают различной точностью. Единственным способом, позволяющим получить необходимый и качественный объем данных о содержании СО2 в атмосфере, является спутниковый метод. Такие методы относятся к косвенным и требуют применения того или иного метода решения обратной задачи, для извлечения искомой информации из измеренных данных.

В данной статье рассматривается метод решения обратной задачи восстановления общего содержания СО 2 из спутниковых данных, основанный на подходе эмпирических ортогональных функций. Спутниковые данные представляют собой измерения отраженного от поверхности Земли солнечного излучения в ближней ИК области спектра.

Постановка обратной задачи

Прямую и обратную задачи можно записать в виде:

У = F ( x , P ) + E y ,                                     (1)

x = B ( y ) + ^E x = B ( F ( x, p ), £ _y ) + ^E x ,                           (2)

где у – вектор измерений в m точках (спектр отраженного солнечного излучения); х – вектор n искомых параметров (общее содержание СО 2 ); p – параметры модели (считаются известными); ε y – шум измерений; F – модель прямой задачи (в нашем случае уравнение переноса излучения в атмосфере); B - оператор решения обратной задачи; X - вектор оценок искомых параметров (априорная информация); ε х – погрешности решения обратной задачи.

Практическая реализация решения обратной задачи требует знания, как это видно из (1, 2), модели переноса излучения и наличия обширной базы априорной информации о параметрах задачи. Понятно, что создание модели, учитывающей полно изменения параметров задачи, возможно лишь для лабораторных условий, а для реальных условий требуется тщательная, кропотливая настройка модели (1) (уменьшение величины ε y ). К тому же в реальных условиях существенную роль играют погрешности измерений ε х . Разработанные в литературе методы решения обратной задачи (например, [3; 5]) рассматривают данную задачу как некорректную, что заставляет применять различные методы регуляризации, которые также используют дополнительную априорную информацию об искомом решении. Изменение каких-либо условий задачи требует пересмотра всех компонент (1, 2), что является затратным по времени и ресурсам, но позволяет в итоге получить требуемый результат.

Для определения общего содержания СО 2 нами был выбран метод эмпирических ортогональных функций (ЭОФ). Он основан на методе главных компонент (МГК) [4; 6; 7], сутью которого является представление измерений в ортонормированном пространстве векторов матрицы ковариации измерений. Как правило, метод ЭОФ применяется для исследования пространственно-временных зависимостей, а для решения обратных задач – очень редко.

По сути, традиционные подходы решения обратной задачи являются параметрическими, основанными на модели решения прямой задачи (1, 2). Предлагаемый нами подход связан с непараметрическим направлением, когда нами ищется взаимосвязь лишь между измерениями и искомыми параметрами.

Описание метода решения обратной задачи

Имеем набор измерений Y , который содержит в себе информацию об искомом параметре (общем содержании CO 2 на оптической трассе формирования сигнала). Между сигналом и искомым параметром существует некоторая функциональная связь, отображенная в виде выражения:

Y ( i , j ) = F ( p ( j )), где Y – измеряемый сигнал; F – функционал, описывающий трансформацию излучения Солнца; p – искомый параметр; i = 1 ... m – число спектральных каналов; j = 1 … n – число измерений в течение определенного времени.

Первым шагом в построении модели на основе ЭОФ является построение корреляционной матрицы:

n

C(i, j) - £ (Y(i, j) - Y (j)) • (Y(l, j) - Y (l)), j=1

где Y – осредненный сигнал для всех измерений n .

Далее корреляционная матрица раскладывается по собственным векторам и значениям:

n

E C (i, j ) E (j, k ) = Л( k ) E (i, k ), j=1

где Е – собственные вектора; Λ – собственные значения.

На основе собственных значений можно построить ЭОФ:

m

G (k, i) = ^ E (j, i )(Y (j, k ) - Y (j)).

j = 1

Линейная регрессия искомой величины с учетом ЭОФ может быть представлена следующим образом:

m1 p(i)=E A(j) G(i,j)+p, j=1

где p – среднее значение искомого параметра и m 1 – новое значение величины m ( m 1 <  m [4]).

Решение этой системы линейных уравнений позволяет найти коэффициенты A и тем самым построить модель для обработки данных измерений в виде:

m1

PR - E A(j)E E< j. j)(Y(l) - Y) + p.(3)

j =1

Результаты применения метода

Для реализации метода ЭОФ нами составлен алгоритм и написана программа, позволяющая считывать реальные (или модельные) спутниковые сигналы GOSAT и восстанавливать общее содержание СО 2 над данной точкой поверхности Земли [1; 2]. Работа с программой состоит из двух шагов: обучение и обработка. На этапе обучения программе необходимо предоставить матрицу сигналов спутника GOSAT за определенный промежуток времени над заданной точкой на поверхности Земли и общее содержание СО 2 , полученное каким-либо способом.

В нашем случае используются данные станций TCCON [10]. В результате работы первого этапа получается набор коэффициентов уравнения (3) A и E . Второй этап связан с решением непосредственно обратной задачи для произвольно поступающих спутниковых сигналов для этой точки на поверхности Земли.

Точность восстановления зависит от количества собственных векторов корреляционной матрицы, которые были взяты из нахождения коэффициентов модели. Эмпирически нами найдено, что для относительной точности восстановления общего содержания СО 2 в районе 1 % достаточно выбрать 200 (из 8 000) наиболее отклоняющихся от среднего значения частот сигнала из канала 2 GOSAT (район 1,6 мкм). И из построенной на их основе корреляционной матрицы взять первые 20 собственных векторов [параметр m 1, см. (3)] для нахождения коэффициентов.

Данные об общем содержании СО 2 брались для станции Lamont сети TCCON. Сеть TCCON является глобальной сетью инструментов измерения количества двуокиси углерода, метана, окиси углерода, окиси азота и других газов в атмосфере Земли.

На рисунках 1, 2 представлено сравнение общего содержание CO 2 по данным станции TCCON Lamont за 2010 г. ( сплошная линия ) и восстановленным значениям по данным GOSAT ( кружки ). Из рисунка 1 видно, что предлагаемый нами метод позволяет восстановить общее содержание СО 2 для исследуемой пространственной точки с хорошей точностью. На рисунке 2 показано сравнение восстановленных значений общего содержания СО 2 и измеренных на станции Lamont. Из рисунка можно определить, что среднее значение отклонений восстановленных и измеренных значений общего содержания СО 2 составляет не менее 1 ppm. Данная точность является достаточной для решения многих прикладных задач оценки изменений климата, переноса газов и др.

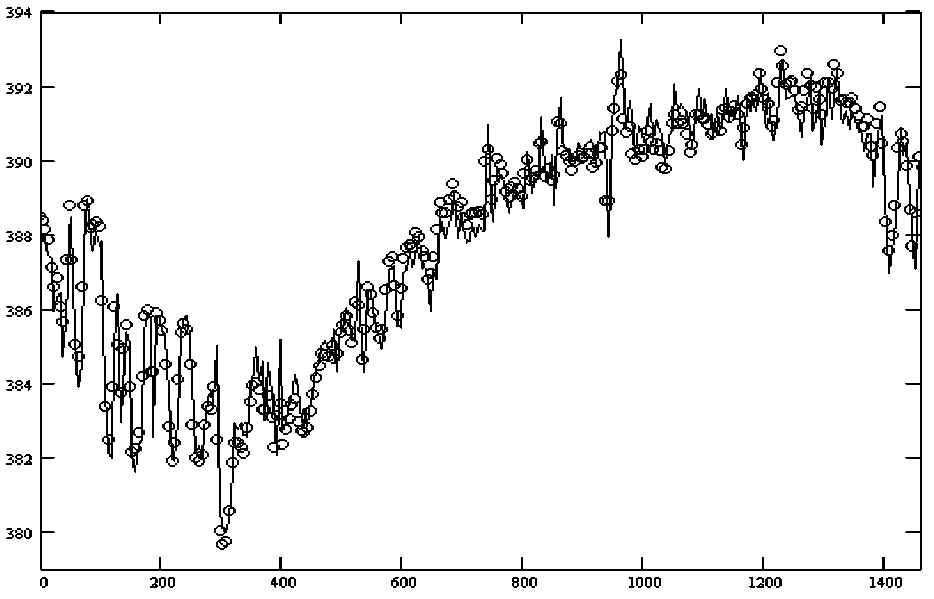
Рис. 1. Общее содержание CO 2 по данным станции TCCON Lamont за 2010 г. ( сплошная линия ) в сравнении с восстановленными значениями по данным GOSAT ( кружки )

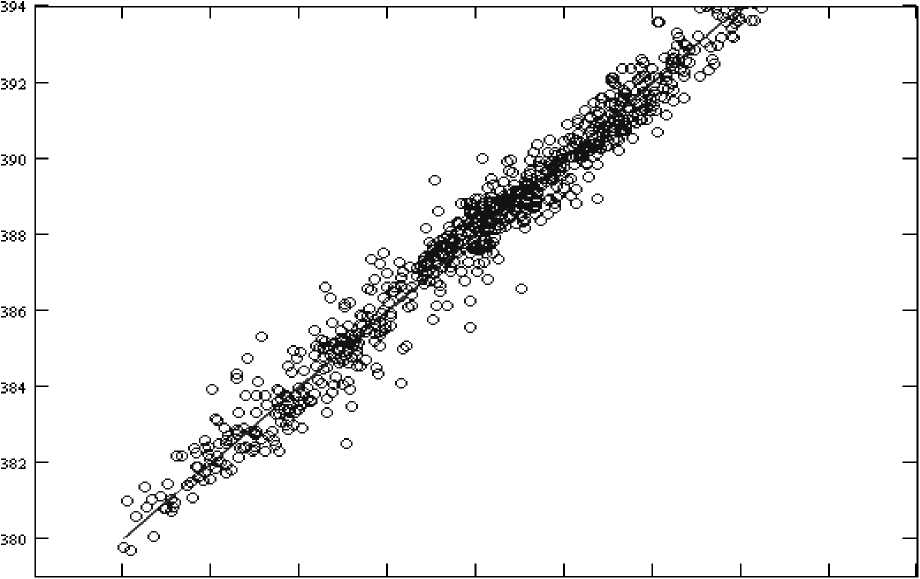
378       380       382       384       386       388       390       392       394       396       398

Рис. 2. Сравнение общего содержания CO 2 по данным станции TCCON Lamont за 2010 г. ( сплошная линия ) и восстановленных значений по данным GOSAT ( кружки )

Заключение

В статье приводится описание метода эмпирических ортогональных функций для решения обратной задачи восстановления общего содержания СО 2 из данных спутникового Фурье-спектрометра GOSAT. Приведены примеры обработки реальных данных и определена точность восстановления.