Метод касательного управления системой «хищник-жертва»

В работе рассматривается участок, содержащий популяцию жертв. Предполагается, что в некоторый момент времени на участке появляется популяция хищников. Появление хищников может быть естественным, как результат миграции в поисках ресурса питания, или искусственным – как результат его интродукции для борьбы с инвазивной популяцией жертв. Последнее является одним из методов борьбы с инвазивными видами [1]. Исследуемая модель представляет собой систему трех обыкновенных дифференциальных уравнений, два из которых относительно численностей популяций хищников и жертв, одно – относительно пищевой привлекательности участка. Впервые понятие пищевой привлекательности участка введено одним из авторов в работе [2]. Предполагается, что популяция хищников мигрирует с участка в случае его недостаточной пищевой привлекательности. Решается задача сохранения популяции хищников на участке за счет изъятия особей популяции хищников и перемещения их на другой участок. В предлагаемой статье развита тема работ [3, 4]. В работах [3, 4] задача сохранения видового состава биосообщества решается соответственно за счет постоянного и периодического/квазипериодического изъятия особей. В настоящей работе предлагается новый метод решения поставленной задачи – метод касательного управления, позволяющий сохранить видовую структуру участка при помощи изъятия особей популяции хищников на одном конечном временном промежутке. Этим представленная работа существенно отличается от работы [3], в которой для сохранения видов производится изъятие особей на бесконечном временном промежутке, и работ [4, 5], в которых подразумевается периодическое изъятие особей на конечных временных промежутках. Очевидно, метод касательного управления позволяет существенно снизить антропогенную нагрузку на биосообщество. Причем в отличии от работ [6, 7], в которых предложены методы оптимального управления, максимизирующие функцию полезности, но изрядно сокращающие численность популяций; лейтмотивом настоящей работы является сохранение видовой структуры биосообщества при помощи наименьшего вмешательства в его естественные процессы.

Доказано существование кривой, разделяющей множество, соответствующее всевозможным значениям начальных численностей, на два: точками одного из которых необходимо управлять для предотвращения миграции хищников, для точек другого множества управление не требуется, видовой состав сохраняется естественным образом. Проведено аналитическое и численное исследование данной кривой.

На основе метода касательного управления в работе построены процессы управления, сохраняющие видовую структуру биосообщества участка. Для реализации процессов используется численный метод, разработанный в [5]. Причем в [5] численный метод разработан для вычисления периода процесса управления, построенного в [4], а в настоящей работе этот метод применяется для нахождения временных промежутков изъятия особей процессов метода касательного управления. Также при помощи численного моделирования из построенных в работе процессов найден оптимальный в смысле минимизации затрат и вмешательства в естественные процессы биосообщества.

1.    Модель и постановка задачи

Пусть х(і),у(і) - численные характеристики популяций жертв и хищников в момент времени t ^ 0 соответственно, причем t = 0 - время появления популяции хищников на участке, x ₀ = х(0),у _о = у (0) - начальные численности жертв и хищников соответственно. Будем считать, что хищники появляются на участке при выполнении условия Х о /у о >  А , где 0 < А - заданная пороговая постоянная, характеризующая минимальное количество жертв, необходимое организму хищника в единицу времени для поддержания всех жизненных функций, то есть участок благоприятен для хищников в смысле объема пищевого ресурса, приходящегося на одного хищника. Пусть при t ^ 0 взаимодействие « хищник-жертва » задается системой Лотки - Вольтерра

Х = x(a — by ), у = y(kbx — m), (1)

где a – коэффициент прироста жертв в отсутствии хищников, bx – количество жертв, потребляемых одним хищником в единицу времени, k – доля полученной с потребляемой хищником биомассой энергии, которая расходуется им на воспроизводство, m – коэффициент смертности хищников в отсутствии жертв, причем, a, b, k, m считаются положительными постоянными ( k <  1 ). Учитывая поведение траекторий системы (1), можно заметить, что существует множество точек z o = (х о ,у о ) Е { х > Ау } таких, что положительные полутраектории с начальными точками z ₀ переходят в область { х <  Ау } , что вызывает тенденцию к миграции хищников c участка, в следствии недостатка пищи. Сделаем важное предположение. Очевидно, миграция хищников c участка не начинается мгновенно, то есть в такой момент времени t * > 0 , что x(t*)/y(t * ) = А , при условии x(t)/y(t) > А, t Е [0,t * ) . В течение некоторого времени, когда x(t)/y(t) <  А , хищники будут оставаться на участке. Для моделирования инерционности начала миграции c участка в [2] предложено понятие пищевой привлекательности участка, а именно, величины n(t) , задаваемой выражением вида

t

t

/ х(т,х _о ,у ₀ )    А

(х(т, х о , у о ) — Ау (т, х о , у о )) dT = J у (т, х о , у о ) ( _у (_т x — ) — А] dT,

где (х(т,х о ,у о ),у(т,х о ,у о )) - решение системы (1), причем (х(0, х о , у о ), у(0,х о ,у о )) = z o и х _о /у _о >  А . Величина n(t) характеризует накопление избытка (при

х(т,Х о ,уо)/у(т,Х о ,у о ) >  А ) или недостатка (при x(т,x o ,y o )/y{т,Х o ,yo) <  А ) пищи для хищников на промежутке [0,t] . Значимость рассмотрения величины отношения x/y при описании динамики популяций обоснована в [8]. Множитель y в подынтегральном выражении позволяет учесть объем популяции хищников.

Будем полагать, что все особи популяции хищников покидают участок в такой момент времени t = t , что x(t)/y (t) <  А , n(t) = 0 , при условии n(t) >  0 , t Е (0, t) . Это предположение основано на принципе ≪ стада себялюбцев ≫ , предложенном в [9] для объяснения скопления особей во времени и в пространстве.

Итак, получаем систему трех обыкновенных дифференциальных уравнений, описывающую взаимодействие ≪хищник–жертва≫, хс = x(a — by), у = у (kbx — m), п = х — Ау

при условии n(t) А 0 , причем последнее уравнение системы получено дифференцированием (2).

В работе предполагается, что для предотвращения миграции хищников с участка производится изъятие некоторой части популяции хищников. Как известно, действия по изъятию широко практикуются для сохранения видовой структуры биосообщества. Пусть и Е { 0 }U R + - интенсивность изъятия хищников с участка, цель которого - сохранение условия n(t) >  0 для любого t >  0 . Описание и будет дано ниже. Тогда системы (1) и (3) примут соответственно вид

Хс = x(a — Ьу),     у/= у (kbx — m — и)                      (4)

и

Хс = x(a — Ьу ), у = у (kbx — m — и), п = x — Ау

при n(t) А 0 . Пусть a(z ₀ ,и) - траектория системы (4), проходящая через точку z ₀ = (x ₀ ,у 0 ) и являющаяся выпуклым овалом. В дальнейшем будем считать, что траектории a(z ₀ ,u) вложены в R + х R и a(z ₀ ,и) С п = { (z, 0) : z Е R + } , где z = (x,y) . Пусть r(t,M ₀ ,и) = (x(t,M ₀ ,и),у(к М ₀ ,и),п(к М ₀ ,и)) - решение системы (5), соответствующее управлению и , причем r(0, M 0 , и) = M ₀ = (x ₀ ,у ₀ , 0) , r(M ₀ , и) = { r(t, M 0 , u),t А 0 } - соответствующая траектория.

Поскольку правые части первых двух уравнений системы (5) не содержат переменную п, то траектории r(M0, и) системы (5) принадлежат цилиндрическим поверхностям S(a(z0,и)) с направляющими a(z0,u) и образующими, ортогональными плоскости {(x,y, 0)} (см. рис. 1). Таким образом, фазовое пространство системы (5) представляет собой дизъюнктное объединение инвариантных цилиндрических поверхно- стей

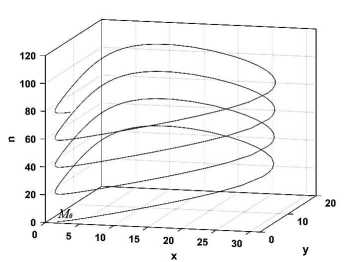
m + u λ <  _ak

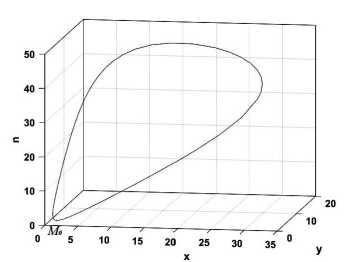
А m+u ak

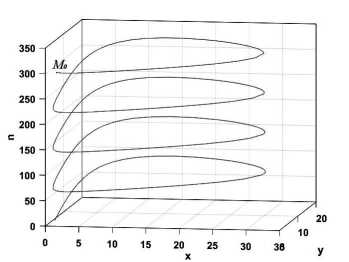
λ> m+u ak

Рис. 1. Траектории r(M ₀ ,u) системы (5) в зависимости от значений параметров a, k, m, u, λ

Определение 1. Допустимым управлением будем называть кусочно постоянную функцию времени и : { 0 } U R + ^ { 0 } U R + , принимающую два значения 0 , и * >  0 . При этом количество переключений u с одного значения на другое не более двух и последнее значение равно 0 .

Смысл предлагаемого управления мотивируется двумя факторами: простотой практической реализуемости и возвратом фазовой точки на цилиндрическую поверхность S(a(z ₀ , 0)) . Второй фактор объясняется желанием нанести меньший ущерб биосообществу, который вызван внешним вмешательством (управлением).

Постановка задачи. Для начальной точки M ₀ = (— ₀ ,y ₀ , 0) , причем х ₀ /у о > А , найти такое допустимое управление u , что:

• 1)    n(t, M₀, и) > 0 при t > 0;

• 2)    n(t, Мо, и) > 0 при t > 0, и > 0.

2.    Предварительные сведения

Замечание 1. Второе условие мотивируется тем, что в процессе управления пищевая привлекательность должна возрастать.

Ниже приведем некоторые свойства траекторий системы (5). Пусть T (z ₀ ,u) — период решения (x(t, z ₀ , и), y(t, z ₀ , и)) системы (4). Обозначим A(t,M ₀ ,u) = n(t + T (z 0 ,u),M 0 ,u) — n(t, М 0 ,и) .

Лемма 1. При любом t Е { 0 } U R ₊

A(_M< 0 .u)=      ' ( m^ - А ) .                  (6)

b ak

Доказательство. Обозначим для краткости T0 = T (z 0 ,u) . Переписывая в виде — = a — by, - = kbx — m — и,	систему (4)
и интегрируя на промежутке [0,T 0 ] , получаем
f T0 тм - аТ0    f T0 ,и - (m + '“)Г 0 J 0 y(t)dt = b .    /0 —(t)dt = kb .
где для краткости (—(t),y(t)) = (—(t, z 0 , и), y(t, z 0 , и)) . Тогда
A(t,M 0 ,и)= /    (—(t) — Ay(t))dt — / (—(t) — Ay(t))dt = /    (—(t) — J 0                          Jo                       tt	Ay (t)')dt.
Учитывая Т 0 -периодичность подынтегральной функции, получаем
A(t, М 0 , и) = / T 0 (—(0 — Ay(t))dt = — AaT0 = aT0 (m±^ 0                         k b         b      b ak	— A ) •

Замечание 2. Лемма 1 позволяет ввести обозначение A(t, М ₀ ,и) = A(z ₀ ,и) .

Следствие 1. Из (6) следует, что в зависимости от значения параметра λ возможно три случая:

n(t, M _o , u) < n(t + T(z _o , u), M _o , u), если A <  ma + u , n(t, M o , u) > n(t + T (z _o , u), M o , u), если A >  m+U , n(t, M o , u) = n(t + T(z _o , u), M o , u), если A = ma + u .

Далее введем луч p = {(x,y, 0) : x = Ay} С п, который разбивает конус п на два открытых конуса: p+ = {(x,y, 0) : x > Ay} С п, p- = {(x,y, 0) : x < Ay} С п. Положение равновесия системы (4) имеет вид r=(m+ua ^                   -7i где 0 C u — константа. Нетрудно показать, что включение R Е р+ равносильно условию A < m+u, R Е p- равносильно A > ma+u, R Е p равносильно A = m+U.

Очевидно, если A = m+ku , то при каждом соответствующем значении u >  0 и A > 0 найдется z _o Е R ++ , при котором овал a(z _o , u) имеет единственную общую точку с лучом p , а именно точку касания Q(u) = a(z _o ,u) П p . Нетрудно показать, что

A(a + m + u) a + m + u

Q^;         6(1 + kA) ,7b(r+kA)) ^{.                      (8)}

Уравнение траектории a(z _o ,u) системы (4), проходящей через точку z _o = (x _o ,y _o ) , имеет вид (при u = 0 см., например, [10])

f = f (x, y, x _o , у о , u) = a In y — by + (m + u) In x — kbx — c = 0,           (9)

где

c = c(x _o ,y _o ,u) = a In y _o — by _o + (m + u) In x _o — kbx _o .

3.    Кривая l(u), аналитическое исследование

В дальнейшем, в настоящей статье, рассматривается случай, при котором на параметр λ наложено следующее ограничение

λ< ^m , ak

что, как отмечено выше, равносильно принадлежности равновесия R системы (1) области p ⁺ : R Е p ⁺ . Это объясняется существенным различием методов решения поставленной задачи управления при условии (10) и при A ^ m/(ak) . Экологический смысл условия (10) состоит в том, что хищнику для поддержания всех жизненных функций в единицу времени необходимо малое количество питательного ресурса (жертв).

Для системы (5) справедлив результат.

Лемма 2. Пусть A < m/(ak).

• а) Пусть a(z _o ,u) П p = { A, B } — такие точки, что x(A) < x(B). Тогда существует единственная точка C = C(a(z _o ,u)) Е a(z _o ,u) П p ⁺ , и соответствующий момент времени t(C ) >  0 такие, что:

al) r(t(C),C,u) = A Е (OQ(u)), где p D (OQ(u)) - открытый промежуток луча p;

• a2) если M E (AC) E a(z ₀ ,u) П p ⁺ , где (AC) — полуоткрытая дуга овала a(z ₀ , и) с концами A и C, то n(t, M, и) >  0 для любого t >  0 ;

• a3) если M E (CB) E a(z ₀ ,и) П р ⁺ , где (CB) — открытая дуга овала a(z ₀ ,u), то существует t(M ) > 0 такое, что при t E (0,t(M)) имеем n(t,M,u) >  0, при t = t(M) — n(t(M ),M,u) = 0.

• b) Пусть a(z ₀ ,u) П p = Q(u) или a(z ₀ ,u) П p = 0 . Тогда n(t,M,u) >  0 для любых M E p ⁺ U { Q(u) } и t >  0 .

Замечание 3. Естественно, A и B - точки пересечения овала a(z ₀ ,u) и луча p , как и точка C , зависят от овала a(z ₀ ,и) . Для краткости используются обозначения, не подчеркивающие этот факт.

Доказательство. a1) Рассмотрим решение r(t,A,u) системы (5). Пусть t(BA) >  0 такой момент времени, что r( - t(BA), A, и) = B' = (x(B),y(B),n(B ‘ )) , причем n(t,A,u) >  0 для любого t E ( - t(BA), 0) . Заметим, что x(B) = Xy(B) x(A) = Xy(A) . Cуществование t(BA) следует из того, что n(0, A, u) = 0 , а фазовая точка, двигаясь по траектории r(A,u) , попадает в точку A из области { (x,y,n) : x < Xy } , в которой n(t) <  0 .

Пусть T(A,и) - период решения (x(t,A,u),y(t,A,u)) системы (4) и A ’ = r( - T(A, и), A, и) . Согласно лемме 1, n( - T(A, и), A, и) = n(0,A,u) — A(A,u) = 0 — A(A,u) <  0 .

Учитывая, что n( — t(BA), A,u) >  0 , получаем существование такого — t* E ( - T(A, и), — t(AB )) , что n( — t * , A, и) = 0 . Тогда, C = r( — t * , A, и) .

Утверждения a2), a3) леммы следуют из непрерывности и единственности решений.

Утверждение б) очевидно, поскольку n(t, M, и) > 0 для M = Q и n = 0 в точке Q .

□

Из леммы 2 следует существование кривой, принадлежащей π и имеющей единственную общую точку с каждой траекторией a(z o ,и) . Обозначим эту кривую 1(и) . Из леммы 2 следует, что 1(и) E p ⁺ . Кроме того, 1(и) примыкает к точке касания Q(u) .

Кривая 1(0) разбивает область р ⁺ на два непересекающихся множества (см. рис. 2): p ⁺ = p + U p + U { 1(0) } , где p + - множество, снизу ограниченное положительной полуосью Ox , сверху - (OQ(0)) U l(0) , p + - множество, снизу ограниченное 1(0) , сверху - (Q(0) + то ) = { (x,y, 0) : x = Xy,x >  x(Q(0)) } . Из леммы 2 следует, что если M o E p + , то управлять системой не требуется, то есть полагаем и = 0 для t ^ 0 . Управление требуется в случае M o E p ^ .В дальнейшем область p ^ будем называть областью ухода .

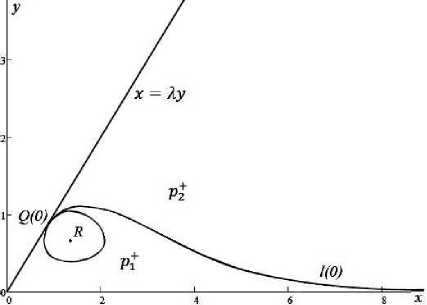
Рис. 2. График кривой 1(0) при a = 1, 0,b = 1, 5, k = 0, 5,m = 1, 0, X = 1, 0

Дадим аналитическое описание кривой l(0) = l . Пусть точка (x i , - i ) Е l , обозначим через t(x i ,y i ,- 1 ) время движения фазовой точки из (x i ,- i ) в точку A = (x 1 ,- 1 ) = (X- 1 ,- 1 ) Е (OQ(0)) (см. лемму 2). Для краткости t(x _i ,y _i ,y ₁ ) = t l . Из (1) получаем

— = a — by, - = kbx — m.

Интегрируя последние равенства на промежутке [0,ti], получаем tl xdT = -1 fln -(ti) + mt\ , /tl ydT = 1 (ati — In xt).(11)

bk       yl               0           bx

Очевидно, по смыслу tl , выполнено равенство tl

(x(t, Mi, 0) — X-(t, Mi, 0))dT = 0, где Mi = (xi,-i, 0). Подставив (11) в (12), получим

In — + Xk In —-1 + (m — XakF = 0.

yl

Подставив в (9) x ₀ = x _i ,y ₀ = y _i ,x = x 1 = Xy 1 , y = - 1 ,u = 0 , получим

(a + m)ln -i — (1 + kX)byi + (m In X — c(xi ,-i)) = g(-i,xi,-i) = 0.

При фиксированных x , y l уравнение (14) имеет два решения, меньшее из которых дает точку A (см. лемму 2). Пусть это решение y 1 = g(xi,y _i ) , то есть A = (Xg(xi,y i ),g(xi,y i' )) . Подставляя - i = g(xi,- i ) в (13), получим

h(xi,y i' ) = (1 + Xk) ln g(xi,y i' ) — In y i — Xk In x i + (m — Xak)t i (xi,y i , g(xi,y i' )') + Xk In X = 0.

Итак, h(xi,y i ) =0 - уравнение кривой l .

4.    Кривая l(u), численное исследование

Разработана программа для построения наименьшего сектора Sl, содержащего кривую l, при заданных значениях параметров a, b, k, m, λ (см. рис. 3). Для любой точки Qi = (x(Q) + ip, (x(Q) + ip)/X) Е (Q, +w), где Q = Q(0); i = 0,1, 2, 3,...; p > 0 поточечно строится траектория f (x,y, x(Qi),y(Qi), 0) = 0 путем разбиения отрезка [xmin,xmax] на d частей точками xj = xmin + j (xmax — xmin)/d и численного решения уравнения f (xj, y, x(Qi), y(Qi), 0) = 0 методом хорд для нахождения соответствующих xj значений -j, где xmin = min{x(t, Qi, 0) : 0 < t < T(Qi, 0)},xinax = max{x(t, Qi, 0) : 0 C t < T(Qi, 0)}, d - натуральное число, j = 0,d. Для каждой точки траектории (xj,-j) Е {(x,y) : f (x,y,x(Qi),y(Qi), 0) = 0,x > Xy} при движении от точки A к точке B против часовой стрелки с помощью метода, предложенного в [5], вычисляется значение интеграла

/о  ⁽ x ^(t

, x j ,- j , ^{0) — X} - ^(t , x j , - j , ^0))dT ,

где (x(0,x j ,- j , 0),y(0,x j ,- j , 0)) = (x j ,- j ),t 2 = max F , где

F = { t : t Е [0,T(Q i , 0)),x(t) = Xy (t) } .

Из леммы 7 ([2, стр. 329],) следует, что для любого i = 1,2,3,... найдется такой отрезок [x j * ,X j * ₊₁ ] , что

Г2 (x(t,

X j * ,y j * , 0) - Ay(t,x j * ,y j * , 0))dT > 0,

/ ⁽ x ^(t

, X j * +1 ,y j * +i , 0) - Ay(t, X j * +i ,y j * +1 , 0))dT <  0.

В силу непрерывности (15) по t ₂ найдется такая точка C(x(C),y(C )) G { (x, y) : f (x,y,x(Q i ),y(Q i ), 0) = 0,x G [x j- * ,X j * +i ] } , что f t ² (x(t,C, 0) - Ay(t,C, 0))dT = 0 . Обозначая через l ₊ кривую, полученную объединением точек (x j * ,y j * ) , для которых интеграл (15) принимает последнее положительное значение, а через l - кривую, полученную объединением точек (x j * + ₁ ,y j * + ₁ ) , для которых интеграл (15) принимает первое отрицательное значение, получим сектор S _l с вершиной в точке Q , ограниченный снизу кривой 1 + , сверху кривой l - (рис. 3), содержащий l . При d G то получим x j * ,x j * ₊₁ G x(C ) и в качестве кривой l можно рассматривать l ₊ или I — . Далее, для определенности, в качестве кривой l будем рассматривать l - . Поскольку l разбивает полуплоскость р ⁺ на два непересекающихся множества р + и р + , причем для предотвращения ухода популяции хищников точками р + нужно управлять, для точек р + видовой состав сохраняется естественным образом ( и = 0 для любого t ^ 0 ), то важно понимать, как изменяется кривая l , как следствие область ухода р + , при варьировании параметров модели. Проведем численное иccледование кривой l .

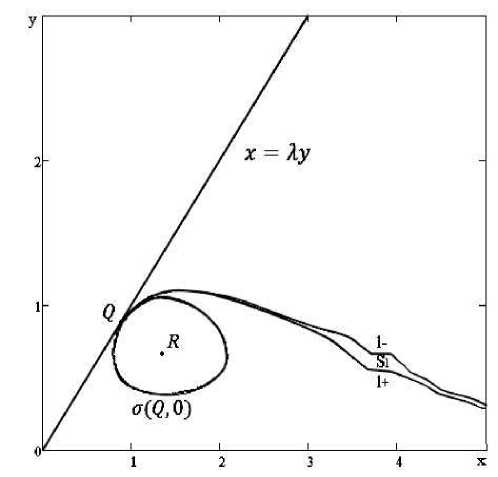
Рис. 3. Наименьший сектор S l , содержащий кривую l , при a = 1,0, b = 1,5, k = 0, 5,m = 1, 0,Л = 1, 0,d = 100, p = 0,1

Пусть начальные значения параметров a = 1, 0, b = 1, 5, k = 0, 5, m = 1, 0, A = 1, 0 . Численно исследуем поведение кривой l при поочередном варьировании каждого из параметров.

Варьирование параметра a

Поскольку кривая l имеет смысл только в случае A < m/(ak) и все параметры, кроме a , фиксированы, то область допустимых значений а есть (0, 2) . Координаты x(Q),y(Q) точки Q (8) - строго возрастающие линейные функции параметра а .

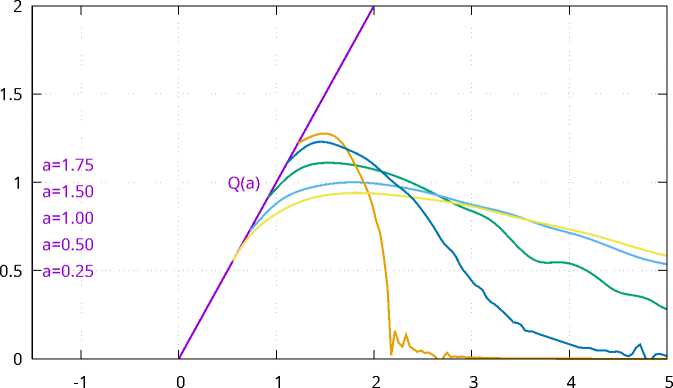
Пример на рис. 4 показывает, как меняется взаимное расположение кривых l при изменении a . Во-первых, кривые l , соответствующие разным значениям a , пересекаются, во-вторых, с ростом параметра a происходит сжатие кривой l вдоль оси Ox , увеличение max { y : (x, y) Е 1 } и области ухода.

x

Рис. 4. Взаимное расположение кривых 1 при различных значениях параметра а Е (0, 2) и постоянных b = 1, 5, к = 0, 5, m = 1, 0, А = 1, 0

Варьирование параметра b

Дифференцированием (7) и (8) по b несложно показать, что координаты R и Q – убывающие функции параметра b . На рис. 5 представлено пять экземпляров кривой l , соответствующих разным значениям b . По результатам численного исследования можно сделать следующие выводы. Во-первых, кривые l , соответствующие различным значениям b , не пересекаются, во-вторых, при увеличении значения параметра b область ухода увеличивается.

Варьирование параметра k

По экологическому смыслу, область допустимых значений параметра к есть (0,1) . Дифференцированием по k координат точки Q (8) нетрудно показать, что координаты точки Q – убывающие функции k . На рис. 6 представлены графики кривых l , соответствующие пяти значениям k . Кривые, соответствующие различным k , не пересекаются. С ростом k происходит увеличение области ухода.

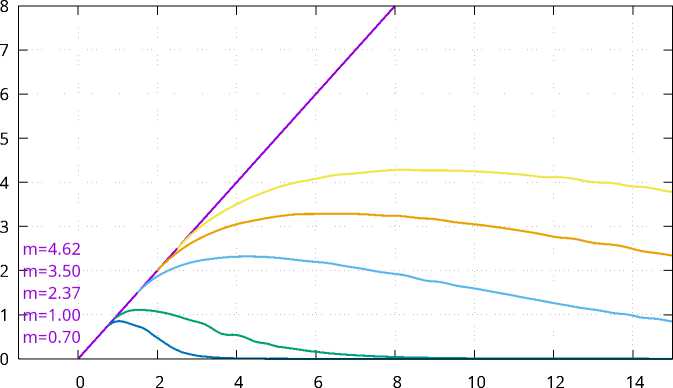
Варьирование параметра m

Поскольку на λ наложено ограничение (10), то область допустимых значений m есть промежуток (0, 5, + то ) . На рис. 7 представлено пять экземпляров кривых 1 , соответствующим различным значениям m . Положение равновесия R с ростом m сдвигается по прямой y = a/b вправо, координаты точки Q возрастают. Анализируя численно полученные кривые l , получаем следующее. Во-первых, кривые не пересекаются, во-вторых, рост естественной смертности популяции хищников приводит к уменьшению области ухода.

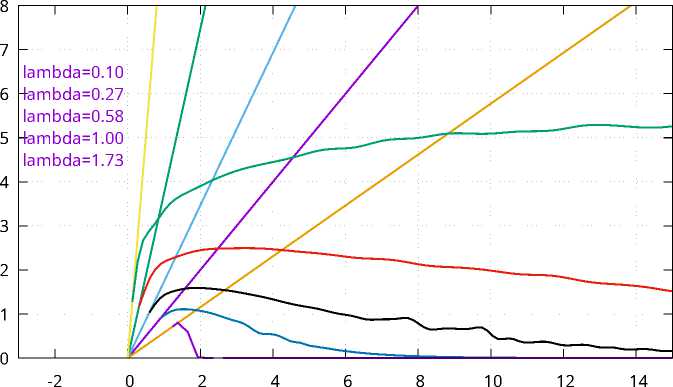
Варьирование параметра λ

В силу того, что 1 существует только при А < m/(ak) , область допустимых значений А есть (0,2) . На рис. 8 представлено пять кривых 1 и пять лучей x = Ay , соответствующих пяти различным значениям А Е (0, 2) . При увеличении A y(Q) убывает, а x(Q) возрастает. Сравнивать области ухода, соответствующие различным А ,

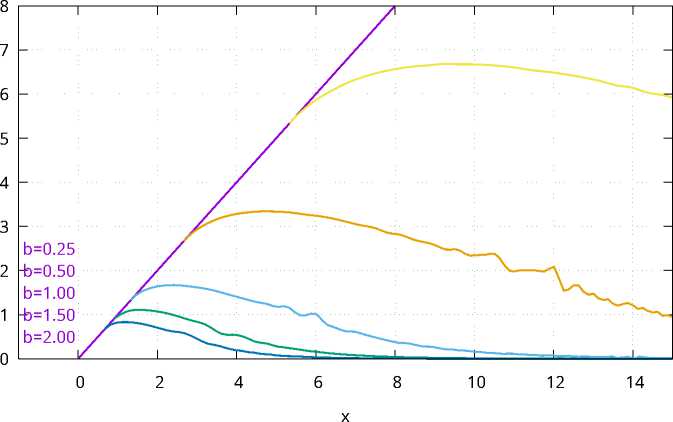
Рис. 5. Взаимное расположение кривых l при различных значениях параметра b и постоянных a = 1,0, k = 0, 5,m = 1, 0, A = 1, 0

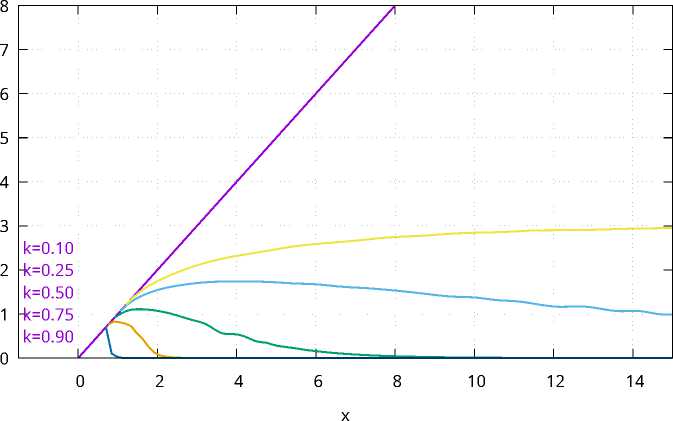
Рис. 6. Взаимное расположение кривых l при различных значениях параметра k и постоянных a = 1, 0, b = 1, 5, m = 1, 0, A = 1, 0

сложно, поскольку, кроме изменения положения кривой l , меняется и положение луча x = Ay .

Таким образом, численное исследование кривой l позволяет получить следующие свойства кривой l , которые мы формулируем в качестве гипотез.

H1. Пересечение кривых l происходит только при изменении значения параметра a .

H2. Область допустимых значений x i - промежуток [x(Q), + то ) .

H3. При x l ^ то y l ^ 0 + 0 .

H4. При возрастании a, b, k и убывании m происходит увеличение области ухода.

С одной стороны при увеличении a жертв становится больше, значит, у хищников становится меньшим желание уйти. С другой стороны, численные результаты

x

Рис. 7. Взаимное расположение кривых l при различных значениях параметра m и постоянных a = 1,0, b = 1, 5, к = 0, 5, A = 1, 0

X

Рис. 8. Взаимное расположение кривых l при различных значениях параметра A Е (0, 2) и постоянных a = 1, 0, b = 1, 5, к = 0, 5, m = 1, 0

показывают, что с увеличением a область ухода увеличивается, то есть вероятность ухода хищников в этом случае увеличивается. Можно показать, что в достаточно малой окрестности (OQ) , принадлежащей р + , нет точек кривой l , что подтверждается численно. С ростом a начальный участок l приближается справа к прямой, параллельной Oy , проходящей через точку, соответствующую max { y l : (x l ,y l ) Е l } ; когда a = 2 , кривая l вырождается в (OQ) , то есть нарушается непрерывное изменение кривой l при изменении a . Из системы Лотки – Вольтерра следует, что при увеличении a увеличивается x , y , но отношение x/y уменьшается, то есть область ухода увеличивается. Этот парадокс согласуется с парадоксом, отмеченным в [10], согласно которому, изымая жертв и не изымая хищников в системе Лотки – Вольтерра, мы не влияем на среднюю численность жертв, а средняя численность хищников при этом уменьшится (см. теорему 5.4 (закон изменения средних) в [10, стр. 151]).

5.    Метод касательного управления

Пусть Mo = (zo, 0) E p+. Для Mo построим процессы управления, при которых выполнены условия 1-2 задачи, причем изъятие предлагается начинать в момент времени t = t1 - время попадания траектории системы (5) на плоскость x = Ay, поскольку при t < t1 n(t, M0, 0) > 0, а при t ^ t1 имеем n(t, M0, 0) С 0. Далее, разделив второе уравнение системы (4) на первое, получим dy   y(kbx — m — u)

dx      x(a — by)

Откуда при x = Ay имеем dy kbλy - m - u dx A (a — by)

Значит, тангенс угла наклона касательной, проведенной к траектории системы (4), соответствующей управлению u , через точку B(x(B ), y(B)) прямой x = Ay - линейная возрастающая функция u ( y(B ) > a/b ). Пусть u * = (k + 1/A)bx(B ) — a — m - управление, при котором dy/dx = 1/A . Таким образом, получаем, что при u < u * не будет выполнено условие 2 задачи, при u ^ u * условие 2 будет выполнено, но поскольку в работе ищется наименьшее антропогенное воздействие, сохраняющее видовой состав биосообщества, то далее рассматривается именно случай касательного управления u = u * .

Процесс управления 1

Пусть B' = r(t 1 ,C, 0) = (x(t 1 ,C, 0),y(t 1 ,C, 0),n(t 1 ,C, 0)) , где t 1 = min F ( F определено в (16)), C E a(z ₀ , 0) П l(0) ,

n(B') = n(t 1 , C,

•E"

(x — Ay)dT,

u * = (k + 1 /A)bx(B) — a — m ; k 1 - наименьшее натуральное число, при котором выполнено неравенство

n(t i , M o , 0) + k i A(B, u * ) > n(B ‘ ).

Теорема 1. Если для любого t E [0,t 1 ) U [t 1 + k 1 T(B,u * ), + to )

• u = 0,

для любого t E [t1 ,t1 + k1T(B,u*)) u = u*, то

• 1)    u – допустимо,

• 2)    n(t, M _o , u) >  0 для любого t > 0, n(t, M _o , u) ^ 0 для любого u >  0 .

Доказательство. 1) Очевидно, что

A(a + m) b(1 + kA) .

x(B) > x(Q) =

Следовательно, x(B )b(1 + kA) λ

> a + m.

Значит, u * >  0 , то есть и - допустимо.

• 2)    При t Е (0,t 1 ) n(t,M 0 , 0) > 0 , следовательно, поскольку n(0,M 0 , 0) = 0 , то n(t,M ₀ , 0) > 0 для любого t Е (0,t 1 ) . Покажем, что при и = и * n(t,M o ,u) ^ 0 . Разделив второе уравнение системы (4) на первое, получим

dy   y (kbx — m — и)

dx      x(a — by)

Подставив в последнее равенство x = x(B) = Ay(B), y = y(B), и = и*, получим dy =1 dx (x(B),y(B)),u=u* A

Следовательно, B - точка касания траектории a(B,u*) и луча р. Из леммы 2 (b) получаем, что при t Е [t1 ,t1 + k1 T(Beu*)), и = и* имеем nl(t,M0,u) > 0 и n(t,M0,и) ^ n(t1, М0,и) > 0. Осталось показать, что n(t,M0,u) > 0 для любого t Е [t1 + k1T(B,u*), +м). Поскольку k1 выбрано таким образом, что n(ti + kiT (В,и*),Мо

и ) =

(x — Ay)dT + k 1 A(B, и * ) > n(B ‘ )

и A(z ₀ , 0) >  0 , то n(t, M ₀ , и) >  0 для любого t Е [t 1 + k 1 T(B, и * ), + м ) .

Процесс управления 2

Лемма 3. Пусть а(М 1 ,и 1 ), a(M 1 , и ₂ ) - траектории ситемы (4), соответствующие разным значениям и 1 ,и ₂ и имеющие общую точку M 1 (x 1 ,y 1 , 0) . Тогда траектории имеют вторую общую точку M ₂ (x ₂ ,y ₂ , 0), причем x ₂ = x 1 .

Доказательство. Уравнения траекторий a(M1 ,и1), а(М1,и2) имеют вид a ln y — by + (m + и1) In x — kbx — (a In y1 — by1 + (m + и1) In x1 — kbx1) = 0, a In y — by + (m + и2) In x — kbx — (a In y1 — by1 + (m + и2) In x1 — kbx1) = 0.

Таким образом, получили систему двух уравнений с двумя неизвестными. Вычитая из второго уравнения системы первое, получим

(и ₂ — u ₁ )(ln x — In x 1 ) = 0.

Поскольку и ₂ = и ₁ , то x = x ₁ .

Из леммы 3 следует, что a(M0, 0) П а(Б,и*) = B U D, причем x(D) = x(B). Известно, что 0 < t1 - первый момент времени, при котором x(t1, M0,0) = x(B). Пусть t1 < t1 + t3 - второй момент времени, при котором x(t1 + t3, Mo,и*) = x(B); t1 +13 < t1 +13 +14 - третий момент времени, при котором x(t1 +13 +14, Mo, 0) = x(B); k2 – наименьшее натуральное число, при котором выполнено неравенство t1                              t1 +t3+t4

/ (x — Ay)dT + k ₂           (x — Ay)dT > n(B').

Теорема 2. Если для любого t Е [0,ti) U (J

t 1 + ^{(p — 1)(t} 3 + t 4 ) + t 3 , t 1 + ^p(t 3 + t 4

p =1 ,k 2

U t i + k 2 (t 3 + t ^ ), + to^

u = 0, для любого t Е U [t1 + (p - 1)^3 + t4),t1 + (p - 1)(t3 + t4)+ t3^

p =1 ,k 2

U = U*, то

• 1)    u – допустимо,

• 2)    n(t, M 0 , u) >  0 для любого t >  0 , n(t, M 0 , u) ^ 0 для любого u >  0 .

Доказательство. 1) Допустимость u доказана в пункте 1 доказательства Теоремы 1.

• 2)    Так как по условию x₀> Xy₀ и при t Е ^0, t1 + k₂(t₃ + t₄)^ имеем n(t, M0, u) = x(t, M0, u) — Xy(t, M0, u) > 0, то n(t, M0, u) > n(0, M₀, u) = 0. Далее, поскольку

  ^n(t1 + k2^(t3 + t4), Mo,

  
  

  u)= [ 0

  
  

  (x — Xy )dT + k₂

  
  

  t1+t3 +t4

  t1

  
  

  (x — Xy)dT > n(B')

  
  

  и A(z₀, 0) > 0, то n(t, Mo, u) > 0 для любого t Е

  
  

  t1 + k2(t3 + t4), +ТО^ .

  
  

  □

  
  
6.    Численное моделирование процессов 1 – 2

Для реализации процесса управления 1 необходимо вычислить t 1 ,k 1 ,T(B,u*) процесса управления 2 - t 1 ,t ₃ ,t ₄ ,k ₂ . При вычислении t i ,k j ,T (B,u*) где i = 1, 3,4 , j = 1, 2 , используется численный метод, разработанный в [5] для нахождения периода траектории системы Лотки – Вольтерра. В [5] предложена модификация метода Вольтерра [11], которая заключается в разбиении траектории a(z o ,u) на четыре дуги, при котором период вычисляется как сумма четырех собственных интегралов с приближенно найденными пределами интегрирования и неявно заданными функциями в подынтегральных выражениях. Причем пределы интегрирования и значения подынтегральных функций вычисляются методом хорд, приближенные значения интегралов находятся методом трапеций. Погрешность каждого из интегралов является суммой погрешностей, вносимых применяемыми методами. В [5] получена формула для оценки сверху погрешностей вычисления интегралов. С более подробным описанием численного метода можно ознакомиться в [5].

Далее процессы управления 1 и 2 строятся для начальных точек Q o = Q , Q i Е { (x,y, 0) : x = Xy } , i = 1,5 . То есть рассматривается случай, при котором t 1 = 0 , следовательно, j’1¹ (x — Xy)dT = 0 . То есть для точек Q i k 1 и k ₂ принимают максимальные значения. Это значит, что расходы на изъятие будут максимальны.

Введем обозначения:

• u i – управление, при котором Q i является точкой касания траектории f (x, y, Q i , u i ) = 0 и прямой x = Xy ;

T(Q i , 0) - период траектории f (x, y, Q i , 0) = 0 ;

n i (B ’ ) определено в (17);

T(Q i ,u i ) - период траектории f (x,y,Q i ,u i ) = 0 ;

A(Q i ,u i )=    Q    ( m + u i — X) ;

• k 1i определено в (18), причем для Q i t 1 = 0 ;

C 1i = k 1i T(Q i ,u i )u i - затраты, необходимые на реализацию процесса управления 1;

• t 3 i , t 4 i определены в описании процесса управления 2;

S ?i = ft ³^ (x - Ay)dT , где x = x(T,Q i ,U i ),y = y(т,Q i ,U i ) , т G [0,t 3 i ] ;

S 4i = t^ ^{+ t 4 i} (x - Ay)dT , где x = х(т, Q i , 0),y = y (т, Q i , 0) , т G [t ?i ,t 3i + t^ ] ;

t i = t ?i + t 4 i , S i = ^S ?i + S 4 i ;

k _{2 i} определено в (19), причем для Q i t 1 =0 ;

C _{2 i} = k _{2 i} t _{3 i} u i — затраты, необходимые на реализацию процесса управления 2.

В табл. 1, 2 представлены результаты, полученные при a = 1,0, b = 1,5, к = 0, 5,m = 1, 0, А = 1, 0 . Погрешность вычисления T(Q i , 0) , T(Q i ,u i ) не превосходит 5.00 х 10 ^- ? , i = 0,5 . Для любой точки Q i ,i = 1,5 , k 1i = k _{2 i} = 1 . Сравнивая численно полученные затраты C 1i и C 2i , можно сделать вывод о том, что оптимальным в смысле минимизации затрат и вмешательства в естественные процессы биосообщества является процесс управления 2. Кроме этого, с ростом i затраты C _{1 i} и C _{2 i} возрастают.

Таблица 1

Зависимость C 1i от положения точки Q i G { (x,y, 0) : x = Ay } , i = 0,1,..., 5 , при a = 1, 0, b = 1, 5, k = 0, 5, m = 1, 0, A = 1, 0

i	Q i	u i	n i (B' i )	т (Q i , 0)	т (Q i ,u i )	A(Q i ,U i )	k 1i	C 1i
0	(0,89,0,89)	0,00	0,00	6,41	6,41	4,27	0,00	0,00
1	(0,90,0,90)	0,02	2,04 х 10 - 5	6,41	6,34	4,43	1	0,16
2	(1,00,1,00)	0,25	1,72 х 10 - 2	6,42	5,82	5,82	1	1,45
3	(1,10,1,10)	0,47	9,25 х 10 - 2	6,46	5,43	7,06	1	2,58
4	(1,20,1,20)	0,70	0,23	6,51	5,14	8,22	1	3,60
5	(1,30,1,30)	0,92	0,40	6,58	4,90	9,32	1	4,53

Таблица 2

Зависимость C _{2 i} от положения точки Q i G { (x,y, 0) : x = Ay } , i = 0,1,..., 5 , при a = 1, 0, b = 1, 5, k = 0, 5, m = 1, 0, A = 1, 0

i	Q i	u i	n i (B' i )	t 3i	S 3i	t 4i	S 4i	t i	S i	k 2i	C 2i
0	(0,89,0,89)	0,00	0,00	1,57	0,24	4,83	4,03	6,41	4,27	0	0
1	(0,90,0,90)	0,02	2,04 х 10 - 5	1,57	0,25	4,75	4,01	6,32	4,26	1	0, 04
2	(1,00,1,00)	0,25	1, 72 х 10 - 2	1,51	0,34	4,07	3,88	5,58	4,22	1	0,38
3	(1,10,1,10)	0,47	9, 25 х 10 - 2	1,46	0,43	3,53	3,82	5,00	4,26	1	0,69
4	(1,20,1,20)	0,70	0,23	1,42	0,51	3,14	3,85	4,56	4,36	1	0,99
5	(1,30,1,30)	0,92	0,40	1,38	0,59	2,84	3,93	4,23	4,52	1	1,28

Далее, численно исследуем, как изменяются затраты C ₂ в зависимости от u . Пусть a = 1,b = 1, 5, k = 0, 5,m = 1, начальная точка M 1 = (1,1, 0) фиксирована, A = 1 , интенсивность изъятия особей растет, причем начальное значение и = и * = 0,25 соответствует касательному управлению. Поскольку, во-первых, точки пересечения траекторий системы Лотки - Вольтерра при и = 0 и и >  u * , M 1 , M 2 , не зависят от значения u , во-вторых, тангенс угла наклона касательной, проведенной к траектории, соответствующей и >  и * , через точку M 1 - линейная возрастающая функция и , то в процессе управления 2 вместо интенсивности изъятия и = и ^* может быть испольнована интенсивность и > и * . В табл. 3 в зависимости от и ^ и * представлены значения t 3 – время движения по цилиндру с управлением, S 3 – величина изменения n при движении по цилиндру с управлением за временной промежуток длины t 3 , k 2

- количество оборотов в процессе управления 2, C 2 (и) - затраты, соответствующие управлению u . Проанализировав результаты, можно сделать вывод о том, что с ростом u время движения по цилиндру с управлением убывает, а суммарные затраты растут. Таким образом, при решении поставленной задачи оптимальным значением и является касательное и = и * . Использование в процессе 2 интенсивности и > и * влечет неоправданные расходы.

Таблица 3

Зависимость C ₂ от u

u	t 3	S 3	k 2	С 2 (и)
0,25	1,51	0,35	1	0,378
0,75	0,84	0,23	1	0,628
1,25	0,57	0,17	1	0,714
1,75	0,43	0,13	1	0,756
2,25	0,35	0,11	1	0,781
2,75	0,29	0,09	1	0,797
3,25	0,25	0,08	1	0,809
3,75	0,22	0,07	1	0,817
4,25	0,19	0,06	1	0,824
4,75	0,17	0,05	1	0,829
5,25	0,16	0,05	1	0,833

7.    Обобщение процесса управления 2

Пусть M 0 = (z ₀ , 0) E p + . С помощью численного анализа выясним, в какой момент времени t E [0,t 1 ] выгоднее переключаться со значения и = 0 на значение и = 0 , соответствующее касательной траектории. Разобьем дугу [M o B ] С a(z o , 0) С p + U p на n частей точками M o = (x o ,y o , 0),M 1 = (x i ,y i , 0 ),..., M n-i = (х п-і ,У п-і , 0),M _n = (x n , y n , 0) = B . Далее для каждой точки M i , i = 0, n , вычисляются:

• 1)    и _і - управление, при котором a(x _i ,y _i ,u _i ) П p = Q i , причем

A(a + m + и і ) a + m + иЛ Q i = ^{Q ( u 1} = (, b(1 + kA) ’ b(1 + kA) ) ■

Вычисляется u _i следующим образом. Подставив в (9)

A(a + m + ui)     a + m + иі x0 = xi,y0 = yi,x =   b(1 + kX)  ,y = b(1 + kX)

и обозначив через и сумму a + m + иі, получим и ln и + Ри + Q = 0,

где Р = ln _bx i ₍₁+ _{kA )} - 1 , 0 < Q = a In jy i + b(y i + kx i ) . При фиксированных X i .y i уравнение (20) имеет два решения, меньшее из которых дает искомое u _i .

• 2)    t ⁱ ₃ , описание которого дано ниже.

Поскольку, в силу леммы 3, a(M0,0) П a(Mi,ui) = Mi U Mi, причем x(Mi) = x(M[) = xi, то найдутся следующие моменты времени: t(M0Mi) E [0,t1] - первый момент времени, при котором x(t(MoMi),Mo, 0) = xi; t(MoMi) + t3 — второй момент времени, при котором x(t(MoMi) + t3, Mo, ui) = xi; t(MoMi) + t3 + t\ — третий момент времени, при котором x(t(MoMi) + t3 + t^,Mo, 0) = xi, t(MiB) - наименьшее время движения фазовой точки траектории a(Mo, 0) из точки Mi в точку B. Заметим, что ti = t(Mo Mi)+ t(Mi B).

• 3)    n(t 1 + t 3 + t 4 , M _o , u) по формуле:

rt i                    ttM O o M i )+ti ₃                    tt(Mo M i )+t 3 +t i ₄

n(t 1 +1 3 + t ^ , M _o ,u) = J (x — Xy)dT + j         (x — Xy )dT + j        i    (x — Xy)dT.

• 4)    Если n(t 1 + t 3 + t ^ ) >  n(B ’ ) , то вычисляются затраты на изъятие особей:

C i = t 3 u-

Создана программа для вычисления затрат, необходимых на реализацию данного процесса управления, i = 0,n (табл. 4). Анализируя численные результаты, можно сделать следующиий вывод. Если начать изъятие с интенсивностью u ₀ при t = 0 , то суммарные затраты на реализацию процесса управления будут минимальны, если же начать изъятие в момент времени t = t 1 , то есть реализовать исходный процесс управления 2, то затраты будут максимальны. Таким образом, получаем, что наиболее выгодно начинать изъятие при t = 0 (рис. 9).

Таблица 4

Зависимость C i от M i Е [M _o B] , i = 0,10 , a = 1, 0,b = 1,5,k = 0, 5,m = 1, 0, X = 1, 0, x o = 2, 0, y o = 0, 9, n = 10 ( n(B ‘ ) = 0, 04 )

x i	y i	u i	i t 3	n(t i +1 3 +1 ^ )	C i
2,00	0,90	0,03	0,40	2,62	0,01
1,90	0,95	0,04	0,46	3,01	0,02
1,81	1,00	0,04	0,50	3,30	0,02
1,71	1,03	0,04	0,52	3,54	0,02
1,62	1,06	0,05	0,53	3,74	0,02
1,52	1,08	0,05	0,53	3,91	0,03
1,43	1,09	0,06	0,53	4,06	0,03
1,33	1,09	0,07	0,51	4,20	0,04
1,23	1,09	0,09	0,49	4,31	0,04
1,14	1,07	0,12	0,45	4,42	0,06
1,04	1,04	0,34	0,38	4,51	0,13

Заключение

Рассмотрена модель, описывающая взаимодействие хищников и жертв на некотором участке, причем по предположению жертвы не покидают участок, а хищники мигрируют с участка в случае его недостаточной пищевой привлекательности. Поставлена задача сохранения видового состава биосообщества данного участка за счет изъятия особей популяции хищников. Доказано существование кривой, разделяющей множество всевозможных значений начальных численностей на два: область ухода – множество, точками которого необходимо управлять для предотвращения миграции

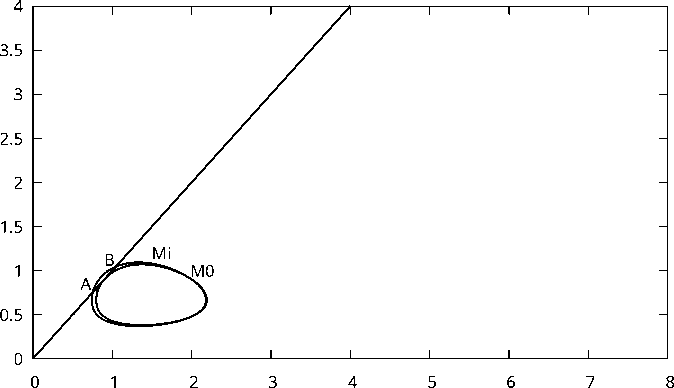
x

Рис. 9. Исходная траектория a(zo, 0) и траектория a(zo,uo), соответствующая оптимальному управлению, в смысле минимизации затрат и внешнего воздействия хищников с участка, и множество, для точек которого управление не требуется, то есть видовой состав сохраняется естественным образом. В работе предложен метод касательного управления и построены соответствующие процессы управления. С помощью численного моделирования найден процесс управления, при котором затраты и вмешательство в естественные процессы биосообщества минимальны.

Работа проводилась при финансовой поддержке РНФ в рамках научного проекта 23-21-00092.