Метод конечных элементов в решении задач теплопроводности

Уравнение теплопроводности [1] широко применяется для описания процесса теплопе-реноса в телах классических форм (пластина, цилиндр, сфера), на практике встречаются объекты сложной формы, и задача их описания решается методом конечных элементов [2].

В общем случае рассматривается некоторое семейство функций, определяемых конечным числом параметров. Среди таких функций нет точного решения задачи, однако подбором параметров можно попытаться приближенно удовлетворить уравнениям задачи и тем самым построить ее приближенное решение. Специфическим в методе конечных элементов является построение семейства функций, определяемых кон ечным числом параметров [3-6]. Выберем такое семейство функций u(x) при X min ≤ x ≤ X max . Интервал X min …X max представляет собой одномерную область существования решения решаемой задачи, который разбивается на конечное число частей (элементов), соединяющихся между собой и с концами интервала в узловых точках (узлах) X i . В пределах каждого элемента задается функция в виде линейного полинома. Она определяется своими значениями u(X i ) в узлах и на концах элемента. Учитывая, что в континуальной задаче функция является непрерывной, то ее значения в каждом узле для соседних элементов должны совпадать. Для этого введем функции округления: L х J - функция пола, которая определяется как наибольшее целое, меньшее или равное x , а ᴎᴍеннᴏ L х J = n о х - 1 <  n <  х ; Г х 1 - функция потолка,

которая определяется как наименьшее целое, большее или равное x , а ᴎᴍеннᴏ L х J = n о х <  n <  х +1. Используя эти функции округления, введем семейство кусочно-линейных непрерывных функций следующего вида:

и (х) = {LФ(х—a )J—Г Ф(х—b )]}• х - a c + (d - c )• b - a

,(1)

где Ф ( х ) - функция Хэвисайда, единичная ступенчатая функция, чьё значение равно нулю для отрицательных аргументов и единице для положительных аргументов; a, b – интервал окна функции u(x) на котором она отлична от нуля ( a ≤ b ) ; c, d – параметры уравнения прямой на интервале a, b . Пример такой функции представлен на графике (Рисунок 1).

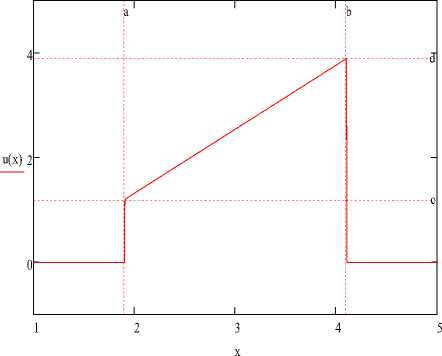
Рисунок 1 - Одномерная линейная кусочно- непрерывная функция

Как видно из представленного графика (Рисунок 1) функция u(x) на границах интервала ( a, b ) обращается в ноль. Используем Ошибка! Источник ссылки не найден. для описания пробной функции на произвольном интервале, задаваемом полушириной h = ( b - а )/2 одномерного единичного конечного элемента относительно узла X i . В этом случае параметры кусочно-линейной непрерывной функции Ошибка! Источник ссылки не найден. соответственно равны а = X i - h , b = X i + h , c = 0, d = 1, а функция приобретает вид:

^фХx )-{ 1^ф[ x ^-( X i ^- h ^)]Н^ф( x ^- X i И-- ;—^{L +}

h

^{+ {}Т^Ф ( x ^- X i Л- L ^ x ^-( X i ⁺ h M-- ;—^L,   ⁽²⁾

h

Функции ф _i (x) изображаются в виде ломаных и определяются конечным числом параметров - своими узловыми значениями. На графике (Рисунок 2) показана функция такого семейства.

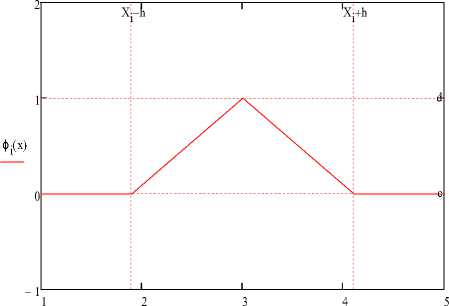
Рисунок 2 - Кусочно-линейная функция Ошибка! Источник ссылки не найден. для решения континуальной одномерной задачи методом конечных элементов

Метод конечных элементов заменяет задачу отыскания функции на задачу отыскания конечного числа ее приближенных значений в отдельных точках-узлах. При этом, если исходная задача относительно функции состоит из дифференциального уравнения с соответствующими граничными условиями, то задача метода конечных элементов относительно ее значений в узлах представляет собой систему алгебраических уравнений. С уменьшением максимального размера элементов увеличивается число узлов и неизвестных узловых параметров. Вместе с этим, повышается возмож- ность более точно удовлетворить уравнениям задачи и тем самым приблизиться к искомому решению. Для линейных задач, когда неизвестные функции и операции над ними входят во все соотношения задачи только в первой степени, метод конечных элементов получил достаточно полное математическое обоснование. В дальнейшем используем линейную задачу, решение которой метод конечных элементов сводит к решению систем линейных алгебраических уравнений. Рассмотрим при-менени е метода для описания одномерного температурного профиля, задаваемого в начальный момент времени (т=0 - начальное условие). В этом случае пробная функция, определяемая уравнением Ошибка! Источник ссылки не найден., представлена линейной комбинацией функций Ошибка! Источник ссылки не найден. с коэффициентами u=u(0):

^{u (} x ^)-^^ u _z. • Ф, -( x ) , ⁽³⁾ i - 1

Для того чтобы u(x i ) = U i во всех узлах X i , функции φ i (x) должны удовлетв орять условиям ф _i (X _i ) = 1 и ф _i (X j ) = 0 для всех узлов X j при y # i . Кроме того, чтобы выполнялись граничные условия первого рода, следует положить u ₀ = u _n+1 = 0 . Метод конечных элементов оперирует в качестве φ i (x) кусочно-полиномиальными функциями, отличными от нуля в пределах небольшого числа элементов вблизи узла X i . Именно это делает метод максимально эффективным. Поскольку u(x) по своему физическому смыслу должна быть непрерывной функцией, выберем ф(х) в виде кусочнолинейных функций, отличных от нуля на двух элементах (Рисунок 2). Каждая такая функция φ i (x), i = 1, 2, …, n, равна единице в X i и нулю во всех остальных узлах. При этом набор функций u(x) будет состоять из непрерывных функций, линейных в пределах элементов с изломами в узлах и определяемых своими узловыми значениями u i , i = 1, 2, „., n . На концах интервала X _min... X _max они обращаются в нуль. Каждую из таких функций можно изобразить в виде ломаной линии. Для определения параметров u i , используемых в уравнении Ошибка! Источник ссылки не найден. , сформируем систему линейных алгебраических уравнений методом Галеркина, интегрируя произведение пробной функции на семейство кусочнолинейных непрерывных функций по области существования решения:

У max

/

^X min

n

т ⁽ x УЕ u i

=1

• T i ( x ) dx

У max

= j [ y ⁽ x ) • T j ⁽ x ^)] dx ^,(4)

^X min

Таким образом, уравнение Ошибка! Источник ссылки не найден. принимает матричную форму:

где j=1,2,…,n; y(x) – функция начального температурного профиля.

В полученной системе линейных алгебраических уравнений определенные интегралы в левой части образуют квадратную матрицу ленточного типа трехдиагональной структуры, образованной двумя видами интегралов на главной диагонали матрицы:

X max                 2 —   _ — ти = IWx)• Ti(x)dx = -—max—-^mn-, (5) 3 n +1

Xmin где i=1,2,…,n.

И над и под главной диагональю:

X max                   1 X   X mk,k+1 = mu_1 = VP1 (x)• T1 _1(x)dx = • max      min-, (6)

6 n + 1

Xmin где k=1,2,…,n-1; l=2,3,…,n.

Упростим задачу, полагая, что y(x)=1 . В этом случае столбец свободных членов p i представляет собой величину, определяемую интегралом:

X max

P i = f T i ( x ) dx = max-----^i^, (7)

n + 1

X min

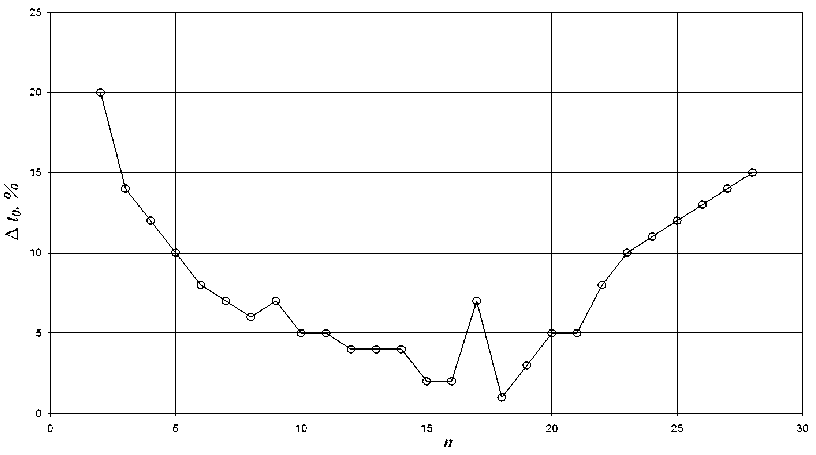
Рисунок 3 – Точность аппроксимации начального температурного профиля в зависимости от числа конечных элементов матричным методом

Из представленных данных видно, что наибольшая точность аппроксимации начального температурного профиля достигается при 12

2 3	1 6	0	0	0		u 1		1
1 6	2 3	1 6	0	0		u 2		1
0	1 6	2 3	1 6	0	•	u 3	=	1 1 (1)
0	0	1 6	2 3	1 6		u n _ 1
0	0	0	1 6	2 3		un		1

Здесь матрица является трехдиагональной, и решение может быть получено методом Гаусса, матричным методом (умножением на обратную матрицу) или прогонки. Для систем малой размерности метод решения не существенен, но с увеличением точности решения необходимо увеличивать число конечных элементов на области существования решения, а это приводит к увеличению числа неизвестных в уравнении (1). Для определения влияния числа конечных элементов на интервале Xmin… Xmax на точность начальной аппроксимации решали систему (1) матричным методом в инженерной среде MathCAD при различных числах n, определяя среднее значение u(x) на этом интервале. Относительная ошибка при различном числе конечных элементов представлена ниже.

18 конечных элементах на области существования решения. При этом относительная ошибка аппроксимации начального темпера- турного профиля составляет 1,5 процента. Если требуется большая точность решения, необходимо использовать метод прогонки , позволяющий решать системы большой размерности без существенных ошибок округления. Этот метод имеет существенные ограничения и применим только для систем линейных алгебраических уравнений ленточного типа. При применении метода конечных элементов ширина полосы ленточной матрицы зависит от нумерации узлов. В некоторых случаях исходная постановка задачи может оказаться настолько плохой, что даже метод конечных элементов не может помочь. В таком случае постановку задачи необходимо менять. При этом имеет место система алгебраических уравнений, в которой малые изменения коэффициентов или свободных членов приводят к значительному изменению решения. Такие системы уравнений носят название плохо обусловленных. Рассмотрим применение метода прогонки для представленной выше системы. Метод прогонки является двухшаговым. Вначале вычисляем вспомога-

α ₀ =

β0

, α ₁ = -          ,

4        4 + α ₀

₂³, β 1

6 - β 0

4 + α ₀

, α

n - 1

4 + α _{n - 2}

, (9)

, ••• , в n-1

6 - β n - 2

4 + α _{n - 2}

, (10 )

Эти величины используются для расчета весовых коэффициентов u i :

u

n

6 - β n - 1

4 + α _{n - 1} ^,

u

n - 1

= ^a n - 1 ■ u n + P n - 1 , - , u 1 = ^a 0 ■ u 2 + P 0 ,      ⁽¹¹⁾

Для определения влияния числа конечных элементов на интервале X min …X max на точность начальной аппроксимации решали систему Ошибка! Источник ссылки не найден. , Ошибка! Источник ссылки не найден. и Ошибка! Источник ссылки не найден. в инженерной среде MathCAD при различных числах n , определяя среднее значение u(x) на этом интервале.

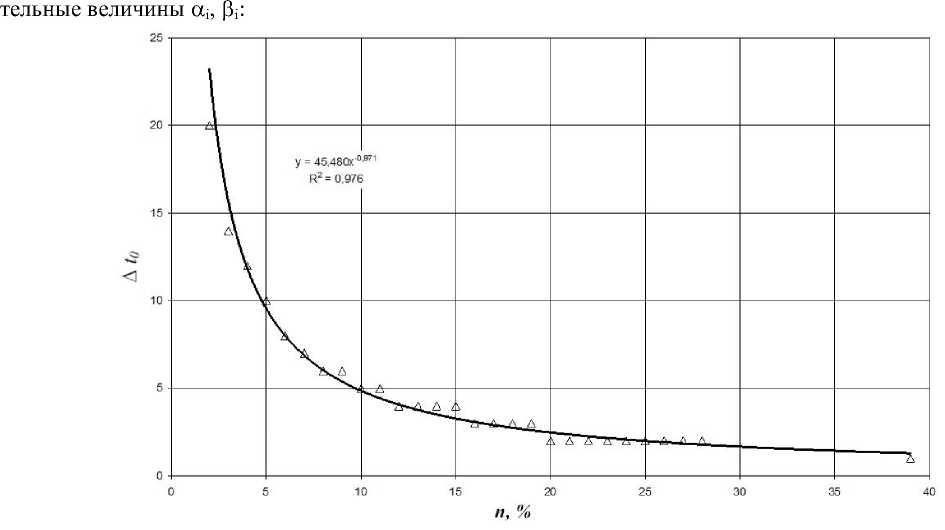
Рисунок 4 – Точность аппроксимации начального температурного профиля в зависимости от числа конечных элементов методом прогонки

Относительная ошибка при различном числе конечных элементов представлена выше (Рисунок 4). Из представленных на рисунке данных видно, что метод конечных элементов позволяет снизить относительную ошибку начальной аппроксимации практически до значения менее одного процента при использовании 40 и более конечных элементов. Ис-

пользуя значения весовых коэффициентов u i как значения неизвестных временных функций u( τ ), можно перейти к решению краевой задачи. В этом случае пробная функция может быть представлена произведением координатных и временных функций:

n

^ ^{( x} ) = Z u i ( ^T ) • V . ^{( x} ) , (2) i = 1

с граничными условиями T (0) = Т (1) = 0. Однако поскольку уравнение содержит вторую производную по координате, а уже первая производная конечного элемента терпит разрывы непрерывности в узлах, воспользуемся следующим приемом. Обозначим R(x) = u( т ) • ф"(x)-u ' ( т ) • ф(x) невязку исходного дифференциального уравнения. Точное решение дает R(x) = 0. Смягчим выполнение этого условия, потребовав, чтобы оно выполнялось только для n функций, которые совпадают с пробными - u( т ) • ф(x) . Такой прием носит название метода Галёркина. Выполним для невязки интегрирование по частям при условии φ(x) = φ j (x) u φ j (0) = φ j (1) = 0 , тогда получим систему первого порядка, как по временной составляющей, так и по координатной:

X

J u(т)• V,"(x)- и‘(тУ Vi(x)]• V,(x)dx = Xmin

У max

• ^- J^[ — u,⁽T ) • ф ; ⁽ x ) • ф ' ⁽ x ^)- и^т ) • V i ^{( x} ) • v , ^{( x ) d}x =⁰, (13) ^X min

Теперь уже в задачу входит u', что дает систему линейных алгебраических уравнений относительно u i вида:

У max

• ^- u i ^{( t} ) • J ^[ v ' ⁽ x ) • V '^{( x} № =

^X min

У max

= u’^T ) • J^[ V i ^{( x} ) • V j ^{( x} '^)dx ,           ⁽¹⁴⁾

min

Интегралы правой части Ошибка! Источник ссылки не найден. представлены выражениями Ошибка! Источник ссылки не найден. и Ошибка! Источник ссылки не найден., а интегралы левой части в полученной системе линейных алгебраических уравнений образуют квадратную матрицу ленточного        типа        трехдиагональной структуры, образованной двумя видами интегралов на главной диагонали матрицы:

Xmax mi, i = J V'i(x )• V'Xx )dx = n + 1,      (15)

Xmin где i=1,2,…,n.

И над и под главной диагональю:

m k,k + 1 = mu - 1 = J V ‘^{( x} ) • V' 1 - 1 ^{( x} ) ^dx = - n V^{1 ,(1} 6 ) 2

X min

Эта матрица симметричная, что характерно для метода Галёркина . Кроме того, произведение отлично от нуля только при j = i, j = i ± 1, когда соответствующие два элемента, которые несут на себе пробные функции, перекрываются. Следовательно, матрица в данном случае оказывается трехдиагональной, так как интегрирование совершается только на двух соседних элементах. Решение полученной системы алгебраических уравнений позволяет найти выражение для производных временных составляющих и получить приближенное решение в форме численного интегрирования, например методом Эйлера. Таким образом, для континуальной задачи метод конечных элементов осуществляет приближенный переход к дискретной задаче на основе соответствующих кусочно-полиномиальных функций, отличных от нуля на нескольких соседних элементах, содержащих узел X i .

Решение (в случае Bi = ^ ) может быть представлено следующей системой дифференциальных уравнений первого порядка:

n+1 —( 21 0 0 0 -(n+Z:) n+1 —( ”+/2) 0 0 (-1)^ 0 -( 21 n+1 -(”+12) 0 о о    -(n+12)   n+1   -(n+12)

0       0       0    - ( n + 12 )    n +1

u ₁ u ₂ u ₃ u n - 1 u_n

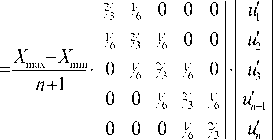
Простейшим вариантом численного интегрирования системы дифференциальных 14

уравнений (37) является метод Эйлера, который может быть представлен следующей рас- четной схемой:

и(ч) U'T - "+1 —("+12) 0 0 0 23 16 0 0 0 —1" uKJ U'T ) u't ' —(+12) n+1 —("+12) 0 0 16 23 16 0 0 U2(Tk—1) uTk ) = U3T ^ 1 0 —("+12) n+1 —("+12). 0 Xnax—Xmin •                                       • "+1 0 16 23 16 0 ^- и3(Тк—1) •At UATk ) UJTk—1) 0 0 —("+12) n+1 —("+12) 0 0 16 23 16 U"-1(тk—к) U" ^k ) u,t -: 0 0 0 —("+12) "+1 0 0 0 16 23 U"T. 1) где Ат - шаг интегрирования системы (37) по времени.

Таким образом, метод конечных элементов позволяет преобразовать континуальную задачу в частных производных к системе линейных кусочно-непрерывных функций с весовыми коэффициентами, зависящими от времени. При этом системы алгебраических уравнений имеют ленточную структуру, что позволяет применять метод прогонки для задач большой размерности, достигая достаточной точности решения при ограниченном числе конечных элементов, покрывающих область существования решения.