Метод конечных элементов в задачах оптимального управления
Автор: Панкратов И.А.
Журнал: Juvenis scientia @jscientia
Рубрика: Механика
Статья в выпуске: 2, 2016 года.
Бесплатный доступ
В статье рассмотрена задача оптимального управления для случая, когда время окончания управляемого процесса фиксировано. Функционал, определяющий качество процесса управления, характеризует затраты энергии на управление. Предложен способ построения приближённого решения задачи, основанный на методе конечных элементов. Приведен пример численного решения задачи.
Метод конечных элементов, оптимальное управление
Короткий адрес: https://sciup.org/14110215
IDR: 14110215
Текст научной статьи Метод конечных элементов в задачах оптимального управления
Постановка задачи
локальные минимумы, где итерационные методы не дают хороших результатов.
Рассмотрим следующую краевую задачу с закреплённым правым концом траектории, описываемой системой линейных дифференциальных уравнений (1)
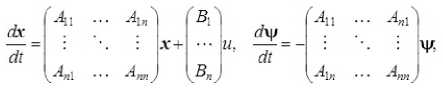
порядка 2 n и 2 n краевыми условиями (2) при г = 0 х = х°; при г = Г х= хк.
Здесь T – заданное время окончания управляемого про-
Метод конечных элементов
Для решения указанной краевой задачи ранее в работах [5-8] применялись метод Галёркина и метод поточечной коллокации с полиномиальными базисными функциями. При этом условия на левом конце траектории удовлетворялись точно, а на правом – приближённо. В настоящей работе рассмотрен случай, когда базисные функции являются линейными и кусочно-определёнными. Пусть отрезок времени [0; T ] разбит M точками на M -1 равных конечных элементов длины h = T / ( M - 1) , тогда линейные базисные функции имеют вид
О, если t < й(ш-2);
' ^q цесса; x= - к xn J
, v=
Vi
– вектора фазовых и сопряжённых
IV n J
N„W= =
переменных соответственно; Aij , Bj – постоянные величины;
» 1 v u = u = 2^BjVj - оптимальное управление, найденное из условия максимума функции Гамильтона-Понтрягина [1]. (Управление иопт соответствует случаю, когда минимизирует-
t-h(m-2) ,, _ _
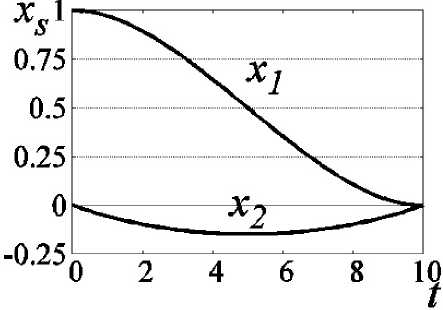
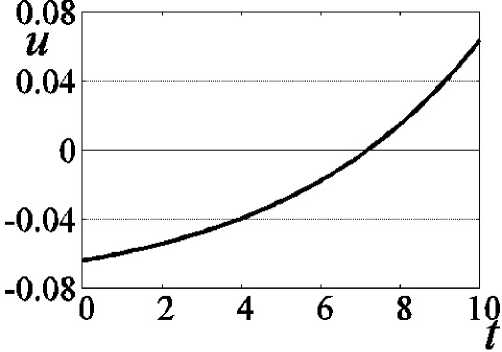
--------если h(_m-2) -----. если h(m-l) О, если t > hm. T ся функционал J=Ju2t , характеризующий затраты энергии.) Традиционно для решения краевых задач оптимального управления (см. например, работы Р.П. Федоренко [2], Ф.П. Васильева [3]) применяются метод Ньютона, метод градиентного спуска [4] и другие итерационные методы. Отметим, что в общем случае не найдены формулы для нахождения неизвестных начальных значений сопряжённых переменных. При этом начальные приближения для значений сопряжённых переменных плохо сходятся к тем значениям, которые доставляют нули невязкам из-за постоянного попадания в их Будем искать приближённое решение рассматриваемой задачи оптимального управления в следующем виде [9]: Подставляя разложения (3), (4) в фазовые и сопряжённые уравнения (1), получим невязки RJ.T] и RV;T] следующего вида (i = 1 ,n): Для получения приближённых равенств R0;т] ~0и R0T] ~0 при tе[0;т] воспользуемся методом Галёркина с одновременной аппроксимацией краевых условий на правом конце траектории, выбрав систему весовых функций Wk = Nk, k = 1,M и требуя, чтобы выполнялись равенства (6) о Второе слагаемое в (6) добавлено для того, чтобы найти решение задачи, приближённо удовлетворяющее условиям при t = T. Учтём граничные условия на левом конце траектории. Так как Wm(/i(r -1)) = <' [1. если m = г; то xj(h(m-1) =MajkNk(h(m-1) = ajm . Таким образом, n уравнений k=1 из (5) нужно заменить на После этого из полученной неоднородной системы вида Ka = f можно будет определить коэффициенты aj,k и тем самым построить решение уравнений (1), точно удовлетворяющее условиям при t = 0, и приближённо - условиям при t = T. Пример численного решения задачи Пусть материальная точка массы m кг движется прямолинейно под действием управляющей силы F(t) и силы сопротивления Fсопр. = - kv, где v - скорость точки. Согласно второму закону Ньютона движение точки описывается урав- d2 x нением mdr = F(t)-k - Введём фазовые координаты x 1 = x (координата точки), x2 = dx / dt = v; управляющий параметр u = F(t) / m и сопряжённые переменные у 1 у2. Тогда краевая задача (1), (2) примет вид В начальный момент времени состояние управляемой си- стемы определяется соотношением . . \N,N,dt \N,N,.,dt (h h\ I ^e-M +e “'e.M +e-l _ _ Je ^ _ _ 3 6 . V «+1ДГ-» c+L,V+c+l ,■ f V V IV V dt — — JJveJ’e+iti< J ^тв+р*е+1ы1 з J б) во втором уравнении системы (8) в) в третьем уравнении системы (8) г) в последнем уравнении системы (8) Вычислив по приведённым формулам компоненты матрицы жёсткости одного конечного элемента, суммированием по всем таким элементам получим компоненты матрицы жёсткости системы (5), (6). Затем заменим первое и (M + 1)-е уравнения (5), (6) на уравнения (7) для точного учёта условий при t = 0. После этого в матрицу жёсткости системы K и столбец свободных членов f останется добавить элементы (остальные элементы столбца f равны нулю). Это позволит приближённо учесть условия при t = T. Для численного решения задачи была составлена программа с помощью математического пакета Scilab [10]. в конечный момент времени При этом оптимальное управление имеет вид um =^2- Отметим, что в матрице жёсткости ke элемента [te;t+1 ] (te+1 = te + h = eh) ненулевыми в данном случае являются лишь следующие компоненты (e = 1 ,M -1): а) в первом уравнении системы (8) Рис. 1. Координата и скорость точки Рис. 1. Координата и скорость точки На рис. 1,2 показаны результаты решения задачи о движении точки под действием управляющей силы и линейной силы сопротивления движению для следующих значений параметров (координата точки измеряется в метрах, скорость – в м/сек): Д о г о о Отметим, что погрешность определения координаты точки меньше, чем погрешность определения её скорости. Отметим также, что при t = T / 2 = 5 сек скорость точки достигает своего минимального значения и t = 5 сек - точка перегиба функции x, = x1 (t). В дальнейшем предполагается применить изложенный выше метод к решению нелинейной задачи оптимальной переориентации орбиты космического аппарата [11, 12].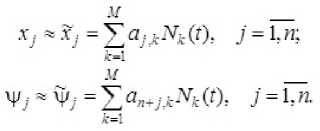
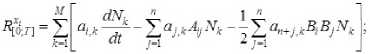
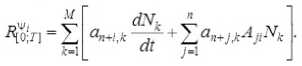
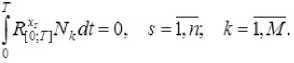
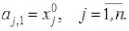
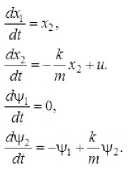
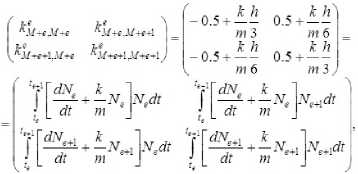
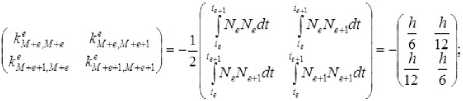
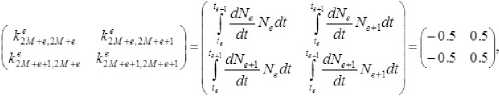

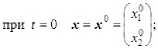
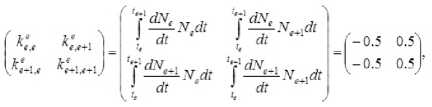
Список литературы Метод конечных элементов в задачах оптимального управления
- Понтрягин Л. С., Болтянский В. Г., Гамкрелидзе Р. В., Мищенко Е. Ф. Математическая теория оптимальных процессов. М.: Наука, 1983. 393 с.
- Федоренко Р. П. Приближенное решение задач оптимального управления. М.: Наука, 1978. 488 с.
- Васильев Ф. П. Численные методы решения экстремальных задач. М.: Наука, 1988. 552 с.
- Моисеев Н. Н. Численные методы в теории оптимальных систем. М.: Наука, 1971. 424 с.
- Панкратов И. А. Решение задач оптимального управления методом взвешенных невязок//Математика. Механика. 2014. № 16. С. 117-120.
- Панкратов И. А. Применение метода Галёркина к решению линейных задач оптимального управления//Изв. Сарат. ун-та. Нов. сер. Сер. Математика. Механика. Информатика. 2014. Т. 14, вып. 3. С. 340-349.
- Панкратов И. А. Об одном методе решения задач оптимального управления//Международна научна школа "Парадигма". Лято-2015. В 8 т. Т. 2: Информационни технологии: сборник научни статии/под ред. О.Я. Кравец. Варна: ЦНИИ «Парадигма». 2015. С. 204-212.
- Панкратов И. А. Применение метода поточечной коллокации в задачах оптимального управления//Актуальные направления научных исследований XXI века: теория и практика. 2015. Т. 3. № 8-3 (19-3). С. 365-368.
- Зенкевич О., Морган К. Конечные элементы и аппроксимация. М.: Мир, 1986. 318 с.
- Алексеев Е. Р., Чеснокова О. В., Рудченко Е. А. Scilab: Решение инженерных и математических задач. М.: ALT Linux; БИНОМ. Лаборатория знаний, 2008. 269 с.
- Челноков Ю. Н., Панкратов И. А. Переориентация орбиты космического аппарата, оптимальная в смысле минимума интегрального квадратичного функционала качества//Мехатроника, автоматизация, управление. 2010. № 8. С. 74-78.
- Челноков Ю. Н., Панкратов И. А. Переориентация круговой орбиты космического аппарата с тремя точками переключения управления//Мехатроника, автоматизация, управление. 2011. № 1. С. 70-73.


