Метод корреляционных плеяд в практике педагогических исследований
Автор: Бондарева Елена Владимировна, Стеценко Наталья Викторовна
Журнал: Математическая физика и компьютерное моделирование @mpcm-jvolsu
Рубрика: Моделирование, информатика и управление
Статья в выпуске: 2 (45), 2018 года.
Бесплатный доступ
В статье рассматривается метод корреляционных плеяд, позволяющий системно проанализировать причинно-следственные связи закономерностей изучаемых признаков. Использование метода показано в практике педагогических исследований в случае необходимости определения структуры всего комплекса изучаемых явлений и его последующего системного описания.
Ранговый коэффициент корреляции кендала, корреляционная матрица, корреляционные плеяды, ведущие признаки
Короткий адрес: https://sciup.org/149129834
IDR: 149129834 | УДК: 510:796.071.3 | DOI: 10.15688/mpcm.jvolsu.2018.2.4
Текст научной статьи Метод корреляционных плеяд в практике педагогических исследований
DOI:
Анализ зависимостей между изучаемыми признаками – одна из важнейших составляющих статистической обработки данных в исследованиях педагогической направленности. Помимо установления количественных зависимостей между изучаемыми признаками современные математические методы позволяют определить структуру всего комплекса явлений и выделить среди них центральные и «периферийные». В то же время эти методы способствуют повышению надежности выводов и дают основания для теоретических обобщений.
Стоит отметить, что педагогические исследования имеют свою специфику, выражающуюся невозможностью в отдельных случаях прямого измерения большинства изучаемых признаков, например таких, как: умственные способности, личностные качества, толерантность, мо- бильность, компетентность. Выделяя такие качества, исследователи имеют возможность составить системное описание явлений. Это стало возможным благодаря применению метода корреляционных плеяд.
Метод корреляционных плеяд впервые был предложен профессором П.В. Терентьевым [5] и в дальнейшем расширен Н.С. Ростовой [4]. Отличительными особенностями метода являются следующие возможности: объективное расположение признаков по степени их значимости и определение структуры взаимосвязей внутри любого комплекса признаков.
Данный метод позволяет системно проанализировать причинно-следственные связи закономерностей изучаемых признаков, а именно: установить уровень, силу, характер и направленность причинно-следственных связей между ними. Причинно-следственные связи закономерностей изучаемых признаков дифференцируют по трем направлениям:
-
– какие характеристики объектов непосредственно вытекают друг из друга и могут не приниматься во внимание;
-
– содержательная информативность изучаемых признаков, характеризующих структуру системы;
-
– нарушение внутренней структуры системы.
Результатом применения данного метода является построение корреляционной плеяды. Перед ее построением необходимо составить корреляционную матрицу – совокупность коэффициентов парной корреляции для всего комплекса явлений. В зависимости от типов случайных величин, представляемых изучаемые явления, в педагогических исследованиях вычисляются коэффициенты корреляции: коэффициент корреляции Пирсона, ранговый коэффициент корреляции Спирмена или ранговый коэффициент корреляции Кендала.
Коэффициент Пирсона находит широкое применение в психологии и педагогике. Однако следует учитывать, что вычисление коэффициента корреляции Пирсона эффективно только в случае справедливости закона нормального распределения вероятностей.
Если выборка содержит независимые объекты, которые обладают двумя качественными признаками, то для оценки степени связи признаков вводят коэффициенты ранговой корреляции Спирмена и Кендала.
Ранговый коэффициент корреляции Кендала дает больше информации об изучаемых признаках, поскольку основывается на вычислении соотношения пар значений двух выборок, имеющих одинаковые или отличающиеся тенденции (возрастание или убывание значений). С помощью этого коэффициента можно судить, попарно сравнивая между собой испытуемых: если у пары испытуемых изменение по X совпадает по направлению с изменением по Y , это свидетельствует о положительной связи, если не совпадает – об отрицательной связи. В этом методе одна переменная представляется в виде монотонной последовательности в порядке возрастания величин; другой переменной присваиваются соответствующие ранговые места. Количество инверсий (нарушений монотонности по сравнению с первым рядом) используется в формуле для корреляционных коэффициентов.
Итак, пусть получена выборка { x 1 i ; x 2 i } , ( i =1, …, n ) двумерной случайной величины ξ = ( ξ 1 , ξ 2) . Ri – ранг (порядковый номер значения случайной величины в ранжированном ряду).
Ранговый коэффициент корреляции Кендала определяется формулой:
4 R n
τ ξ 1 ξ 2 = n ( n - 1) , где R = ∑ i = 1 R i .
Из вычисленных коэффициентов составляется корреляционная матрица. Результаты корреляционных связей в полученной матрице следует графически изобразить, то есть построить корреляционную плеяду, для чего необходимо изучаемые признаки упорядочить:
-
– выбрать 2 наиболее сопряженных признака (с максимальным значением τ ij );
-
– найти в строках i и j следующий наиболее сопряженный признак.
Эти действия следует выполнять до тех пор, пока не будут задействованы все признаки.
Визуально корреляционная плеяда представляет собой фигуру, составляющими которой являются:
-
– вершины, соответствующие признакам и обозначающиеся цифрами или сокращенными названиями признаков;
-
– соединяющие вершины линии, соответствующие статистически значимым связям и графически выражающие уровень значимости связи.
При построении корреляционной плеяды исследователю следует придерживаться определенных рекомендаций (рис. 1).

Рис. 1. Рекомендации к построению корреляционных плеяд
Немаловажное значение имеет правильная интерпретация полученных графических изображений взаимосвязей между признаками. Признаки, имеющие много связей, рассматриваются как ведущие (центральные). Им может быть приписано большое функциональное или системообразующее значение. Признаки, имеющие мало связей, рассматриваются как периферийные. Сама отдельно взятая цепочка связей не может быть однозначно интерпретирована. Имеет смысл рассматривать последовательность удаления признаков от некоторого центра [3].
Покажем на примере возможность применения метода корреляционных плеяд в педагогическом исследовании.
В ходе педагогического эксперимента, проводимого в Волгоградском государственном университете в процессе подготовки специалистов прикладной информатики в экономике, уровень компетентности студента определялся сформированностью критериев, позволяющих получить наиболее полное представление о качественном и количественном состоянии составных компонентов профессиональной компетентности. Группой экспертов по каждому критерию был выделен ряд показателей, характеризующих наиболее существенные и необходимые проявления диагностируемого качества [2, с. 111].
Покажем использование метода корреляционных плеяд для изучения структуры комплекса девяти выделенных признаков, характеризующих сформированность профессиональной компетентности студента-выпускника (см. табл. 1).
Данные наблюдений представлены матрицей, в которой столбцы соответствуют признакам, строки – наблюдениям (см. табл. 2). Шкала оценивания – от 1 до 3.
Таблица 1
Комплекс признаков, характеризующих сформированность профессиональной компетентности студента
|
Краткое обозначение признака |
Содержание признака |
|
К1 |
Наличие мотивов профессиональной компетентности, характеризующих потребность студента в знаниях, в овладении эффективными способами формирования профессиональной компетентности |
|
К2 |
Настойчивость, активность, умение выдерживать нагрузки, упорство в затруднительных ситуациях, целеустремленность (характеризуют волю) |
|
К3 |
Рефлексия достигнутого уровня развития как личности и профессионала |
|
К4 |
Рефлексия качества результатов реализации модели технологично спроектированной профессиональной деятельности |
|
К5 |
Объем, полнота, точность, понимание, осмысленность знаний дисциплин экономики и информатики, прочность усвоенного материала |
|
К6 |
Умение решать нестандартные задачи создания, анализа и сопровождения профессионально ориентированных информационных систем |
|
К7 |
Быстрота актуализации нужных знаний |
|
К8 |
Способность к организации профессионального общения |
|
К9 |
Продуктивное участие в общении, толерантное восприятие партнера |
Таблица 2
Матрица наблюдений признаков, характеризующих сформированность профессиональной компетентности студента
|
К1 |
К2 |
К1 |
К2 |
К3 |
К6 |
К7 |
К8 |
К9 |
|
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
|
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
|
2 |
3 |
2 |
1 |
1 |
1 |
1 |
3 |
3 |
|
3 |
3 |
3 |
2 |
3 |
3 |
3 |
3 |
3 |
|
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
3 |
2 |
1 |
2 |
2 |
2 |
3 |
2 |
|
2 |
3 |
2 |
2 |
2 |
3 |
2 |
2 |
2 |
|
3 |
3 |
3 |
3 |
3 |
3 |
2 |
3 |
3 |
|
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
|
3 |
3 |
3 |
1 |
3 |
3 |
3 |
3 |
3 |
|
2 |
3 |
2 |
3 |
2 |
3 |
3 |
3 |
3 |
|
1 |
2 |
2 |
2 |
2 |
2 |
2 |
3 |
2 |
|
1 |
3 |
1 |
1 |
1 |
3 |
2 |
2 |
2 |
|
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
|
2 |
3 |
2 |
1 |
1 |
1 |
1 |
3 |
3 |
|
3 |
3 |
3 |
2 |
3 |
3 |
3 |
3 |
3 |
|
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
3 |
2 |
1 |
2 |
2 |
2 |
3 |
2 |
|
2 |
3 |
2 |
2 |
2 |
3 |
2 |
2 |
2 |
|
3 |
3 |
3 |
3 |
3 |
3 |
2 |
3 |
3 |
|
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
|
3 |
3 |
3 |
1 |
3 |
3 |
3 |
3 |
3 |
|
2 |
3 |
2 |
3 |
2 |
3 |
3 |
3 |
3 |
Результаты исследования представлены в виде численных значений корреляционной матрицы (табл. 3). Пороговое значение значимости коэффициента корреляции, определяющее наличие связи в данном исследовании, было выбрано равным 0,3.
Таблица 3
Корреляционная матрица коэффициентов Кендала
|
К1 |
К2 |
Р3 |
К4 |
К5 |
К6 |
К7 |
К8 |
К9 |
|
|
К1 |
1,000 |
||||||||
|
К2 |
0,548 |
1,000 |
|||||||
|
К3 |
0,923 |
0,832 |
1,000 |
||||||
|
К4 |
0,622 |
0,850 |
0,596 |
1,000 |
|||||
|
К5 |
0,848 |
0,504 |
0,940 |
0,862 |
1,000 |
||||
|
К6 |
0,649 |
0,639 |
0,644 |
0,732 |
0,779 |
1,000 |
|||
|
К7 |
0,684 |
0,553 |
0,732 |
0,622 |
0,832 |
0,857 |
1,000 |
||
|
К8 |
0,561 |
0,776 |
0,749 |
0,415 |
0,613 |
0,435 |
0,827 |
1,000 |
|
|
К9 |
0,827 |
0,783 |
0,822 |
0,554 |
0,660 |
0,555 |
0,648 |
0,862 |
1,000 |
На данном этапе исследования анализ полученной информации позволил сделать следующие заключения:
-
1) отрицательных связей не выявлено;
-
2) наличие большого количества положительных значимых связей.
Структура комплекса изучаемых признаков по данным корреляционной матрицы представлена на рисунке 2 в виде графа – геометрической схемы, включающей две и более точки, обозначающие один из девяти признаков комплекса. Эти точки соединяются линиями, если между ними установлены значимые линейные корреляционные связи. Для этого весь диапазон значений коэффициентов парной корреляции условно разбивается на несколько интервалов (в данном случае: высокие – более 0,8, средние – 0,6–0,8, низкие – от порогового значения, определяемого исследователем, до 0,6). Для высоких значений они показаны жирными линиями, для средних – тонкими сплошными, а для низких – прерывистыми.
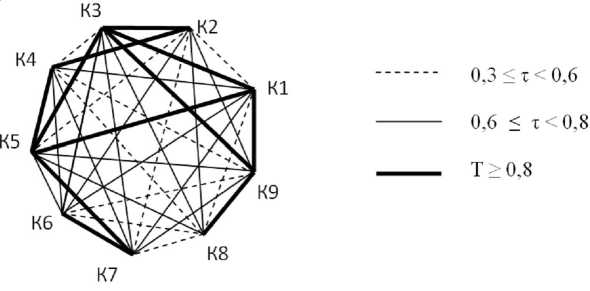
Рис. 2. Корреляционная плеяда
В результате построенной корреляционной плеяды можно заключить, что присутствует сильная корреляция между следующими парами признаков: К1 и К3; К1 и К5; К1 и К9; К2 и К3; К2 и К4; К3 и К5; К3 и К9; К4 и К5; К5 и К7; К6 и К7; К7 и К8; К8 и К9. Стохастические связи между указанными парами могут считаться установленными. На основе полученных результатов можно утверждать о достаточности и значимости выявленных показателей в составе профессиональной компетентности будущего специалиста прикладной информатики в экономике. Присутствующая сильная и устойчивая корреляция между этими парами показателей указала на необходимость уделить особое внимание обнаруженным связям в дальнейшем исследовании.
Список литературы Метод корреляционных плеяд в практике педагогических исследований
- Бондарева, Е. В. Об использовании многомерного корреляционного анализа в педагогическом исследовании / Е. В. Бондарева // 8th International Scientific Conference «European Applied Science: modern approachesin scientific researches»: Papers of the 8th International Scientific Conference (January 30, 2014, Stuttgart, Germany). - Stuttgart, 2014. - P. 24-28.
- Бондарева, Е. В. Формирование профессиональной компетентности будущих специалистов прикладной информатики в экономике: дис.... канд. пед. наук / Бондарева Елена Владимировна. - Волгоград, 2005. - 208 с.
- Ковалева, И. Л. Метод корреляционных плеяд: методические указания к лабораторной работе для студентов специальности 1-40.01.02 «Информационные системы и технологии» / И. Л. Ковалева, Л. В. Федосова. - Минск: Изд-во БНТУ, 2014. - 22 с.
- Ростова, Н. С. Корреляции: структура и изменчивость / Н. С. Ростова. - СПб.: Изд-во С.-Петерб. ун-та, 2002. - 308 с.
- Терентьев, П. В. Метод корреляционных плеяд / П. В. Терентьев // Вестник Ленинградского университета. - 1959. - № 9. - С. 137-141.


