Метод косвенных предпочтений формирования весов критериев с многоуровневой структурой

Принятие управленческих решений часто сопряжено с решением прикладных задач оценивания и выбора эффективных объектов (вариантов решений, альтернатив, стратегий), которые относятся к классу многокритериальных задач. На практике к этому классу относятся задачи: построения рейтингов компаний, банков; оценки эффективности деятельности коллективов в организационных системах; синтеза сложной технической системы.

Для объектов с многоуровневой структурой характерно представление системы критериев в виде иерархического дерева [1-3]. При этом возникает проблема оценки количественной важности локальных критериев, входящих в вершину более высокого уровня.

Обзору и классификации методов формирования весовых коэффициентов посвящено большое число работ [4-9]. Известно более двадцати различных методов определения весов, часть из которых подробно рассмотрена в статье [8].

Настоящая статья посвящена развитию методов косвенного измерения предпочтений критериев в шкале отношений [10].

1 Определение важности критериев

Одна из первых методик решения многокритериальных задач с многоуровневой структурой была разработана для оценки эффективности вариантов прогнозирования и планирования при разработке сложных научных и научно-технических программ (ПАТТЕРН, PATTERN 1 , США) [2]. Методика включает построение дерева целей, которое служит для оценки относительной важности критериев, и применение прямого метода экспертного оценивания количественных весов критериев.

Оценки количественной важности локальных критериев, входящих в вершины более высокого уровня, эксперты проставляют на бланке (в долях единицы). Процедура определения коэффициентов проходит в несколько туров, пока не будет согласована со всеми экспертами. Пересчёт их в глобальные веса для концевых (висячих) вершин дерева осуществляется перемножением весов всех вершин, лежащих на пути, ведущем к данной вершине. Для каждой альтернативы (объекта, проекта, варианта) находится агрегированная оценка, равная сумме произведений глобальных весов и оценок критериев в концевых вершинах дерева.

В соответствии с теорией измерений [11] веса важности критериев могут быть измерены в градациях различных шкал, например: в номинальных шкалах с двумя градациями «равноважны» и «неравноважны»; в количественных (разности, отношений) с различными весами важности (предпочтительности) по числу критериев.

Понятие важности критериев c точки зрения теории измерений можно рассмотреть следующим образом. Пусть объекты множества Д = {a _q^-.q = 1, п_А } оцениваются по f j EF = {f t , ■■■, f m ^} критериям.                                                           ____

Определение 1. В количественной шкале отношений критерий ft, i = 1, т, считается бо лее важным, чем критерий fj (обозначение ft > fj), если количественный вес wt = w(ft)

W [

W j

критерия f t будет превосходить количественный вес W j = w(f j ) критерия f j в

> 1 раз, т.е.

f t >  f j ^ w(f ) >  W(f j )

и наоборот, менее важен, если — < 1, а при — = 1, т.е. равенстве весов, критерии равноваж-Wj            Wj ны ft * fj ^ W(ft) = W(fj).

Известно следующее определение однородных критериев по важности [12, 13].

Определение 2 . Утверждение «критерий K_t важнее критерия K j » (обозначение i > j) означает, что каждая векторная оценка х, в которой х_t > X j , предподчительнее, чем х ^ .

Здесь х^ - обозначение векторной оценки, которая получена из векторной х =

(х_Т, ..., х_т ) оценки, например, если х = (5,4, 3,4), то х²³ = (5, 3,4,4).

Замечание 1 . Сравнение определений 1 и 2 приводит к выводу о том, что определение 1 не привязано к векторным оценкам, в отличие от определения 2. Можно показать, что утверждение «каждая векторная оценка х, в которой х_t >  X j , предподчительнее, чем х^tj» следует из предпочтительности критерия f t относительно f j и условия X t >  X j .

¹ PATTERN (от англ. Planning Assistance Through Technical Evaluation from Relevans Number ) поддержка планирования посредством относительных показателей технической оценки.

Действительно, пусть критерий / важнее критерия /, т.е. для количественных весов справедливо неравенство: wt >  Wjo Очевидно, векторы х и х ^tj несравнимы по предпочтительности, однако в силу однородности шкалы измерения в задачах векторной оптимизации они сравнимы по аддитивной свёртке [5]:

F (x,w) = 2™! wsxs, где ws = w(fs) - количественный вес критерия f, s = 1, т; х = (x1,..., Xs,..., хтУ Агрегированные оценки векторов х и хij представляются в виде:

F (x, w) = АХ[Х+ + WjXj + Z^m s=i, w_sx_s.   F(x ^ij, w) = w , x_; + WjX_t + Z^m s=i, w_sx_s.

s * j , s * i                                                           s * j , s * i

Разность F (x, w) — F(x ^ij, w) агрегированных оценок х и х ^lJ имеет вид:

F (x,w) — F (x ^ij, w) = (w_ix_i + W j X j ) — (w_iX j + w_;x) = (w_i — W j )(x_i — X j ) > 0, т.е. векторная оценка х, в которой X i > X j , предподчительнее, чем х^ij в силу предпочтительности критерия f i над критерием /.

В работе [14] в качестве количественных весов предлагается использовать числовую последовательность П. Фишберна [15]:

2 (m+i - i) т (т+i) '

где i - номер критерия в порядке убывания его важности, при этом 2™ i W i = 1.

В работе [16] предложена формула для вычисления задающих коэффициентов в виде:

^715

■ {

п² C_s + 2Tl—1 п ² (п - i)

при S = 1, при 1 < s < и,

где 5 - группа важности, a_ns - универсальные коэффициенты важности в политике выбора для n критериев, в которой каждая группа важности включает ровно один критерий. Задающий параметр C_s для и = 2, 3,4, ., 10 принимает значения 0, 6, 18,^, 216.

В силу того, что нормированные веса частных критериев характеризуют долю вклада в обобщённый критерий и формируются обычно методами экспертного оценивания [8], то вследствие этого формулы (1) и (2) не могут быть применимы в качестве весов критериев, связанных с различными предметными областями решаемых многокритериальных задач.

Таким образом, предпочтительность одного критерия относительно другого, а также их количественные веса не зависят от векторных оценок объектов и определяются экспертами. В дальнейшем для оценки количественной важности критериев используется определение 1.

экспертов, участвующих в ранжировании, находится результирующее ранжирование (медиана Кемени), метод формирования которого представлен в работе [17].

Для деревьев в основном применяются два способа перечисления: «по ветвям», когда индекс вершины указывает путь к этой вершине; «по уровням», когда по очереди рассматриваются все уровни сверху вниз, а вершины одного уровня нумеруются подряд слева направо. Способом перечисления «по ветвям» дерево задаётся в виде множества упорядоченных вершин [18]:

ID ={ g,D }, где g = {Fo, Fj ,-, Fj jI jk = 1, nj1-j; к = 1, ng} - множество вершин (критериев), в ко торых индекс j1 -j к вершины Fj j указывает путь к этой вершине от корневой вершины Fo (к = 0); {0,1, -, к, -, ng} - номера уровней в дереве;

D = {(Fj- _-j k-v Ff-jk) । jк = 1, nj_1-j_k_₁; k = 1, ng} — множество дуг, в которых множество вершин {F j _- j _k}, инцидентно вершине F j _-j_к

Fo — глобальный (обобщённый) критерий верхнего (нулевого) уровня иерархии;

F j - групповые критерии 1 -го уровня иерархии, являющиеся концевыми вершинами множества дуг {(F_o, F j ) \ j₁ = 1, n₀ }' n 0 — число дуг, инцидентных вершине F ₀;

Концевые вершины  ng-го  нижнего уровня условно обозначены строчными ми fj1-jn. Каждому Эs эксперту, где s = 1, nэ , предъявляется множество подкритериев

^F = ^F i i -j k-1 ^

на к -м уровне иерархии упорядоченных по убыванию важности и входящих в вершину ^Fj к -1 = ^Fj i -j k -1 ^:

F_t >F₂>_ >F ^ > „> F . . _k _  $ = 1, j _k _ i , ^jj k -1 = ^j j i -j k -1 ,           ⁽³⁾

где >  - обозначение нестрогого предпочтения, которое означает для пары критериев строгого предпочтения (обозначение >) или отношение равнозначности (обозначение «).

{Fi_-jfc-i₁, —,Fj_1-jk-inj₁ j_k } - множество подкритериев (к — 1)-го уровня, входящих в вершину Fj j _к к-го уровня; j _к = 1,nj ;к = 1, ng. Подкритерии, входящие в вершины более высокого уровня, упорядочиваются по важности:

> — > F,             V j_k= 1,n      ;k = 1,ng.

J 1 —j k-1 ¹              j 1 - ^j k- l^fii i-_/k_-1      ^{K          j} 1 - ^j k- 1               ^g

Шаг 2. Экспертное оценивание степеней превосходства смежных критериев на к - м уровне иерархического дерева в шкале отношений. Эксперту предъявляется множество подкритериев F ^ = F j^ _-j_k-₃X , на к -м уровне иерархии упорядоченных по убыванию важности и входящих в вершину Fj^ = Fj^ _-j_k-i (см. выражение (3)).

Результаты сравнения w ^,^ ₊₁ «

w^

w^+i

смежных пар подкритериев {F, F₊₁} на к -м уровне

иерархии, входящих в вершину F_k_₁ = Fi_-j k-i

нее неизвестны, представляются в виде (

(wi^z/w 23 ^,-^{, w}F+i ^,-^,w

-

, локальные веса wI ^ = w 1(F) которых зара) наддиагональных элементов

,-1.^п;ь .k-i    .k-i

квадратной матрицы попарного сравнения смежных подкритериев {F, F+F ^F

’   ’        Jk-l

Н, ^+1 ]:

	/  1	w; ,2		.         0    \
^F;   =	1/w 1',2		w 2,3		°.
Jk-1	: \0			1/w ; /   njfc_1	-1njk n jk_ 1 1n jky

При этом количественная оценка w /, / ₊₁ означает, что эксперт считает критерий F / важнее критерия F / ₊₁ (F / >  F / ₊₁) в w /,/ _{+ 1} « wZ / /w I / _{+ 1} раз, если w /,/ _{+ 1} > 1, а при w /,/ _{+ 1} = 1 критерии равноважны (F / * F / _{+ 1} ).

Исходя из свойства обратной симметрии, равенство w / _{+ 1} / =---- < 1, означает, что ко

, ?+1

личественно критерий F / _{+ 1} в w / _{+ 1} ,/ раз менее важен критерия F / .

При таком подходе достаточно всего лишь (п / — 1)-го экспертного сравнения вместо ⁽ⁿ j     )

——— при попарном сравнении как, например, в методе анализа иерархий (МАИ) Т. Саати [1].

Шаг 3. Формирование элементов столбцов матрицы коэффициентов важности критериев. По экспертным оценкам (4) предпочтительности смежных критериев, входящих в вершину критерия более высокого уровня иерархического дерева, формируются элементы столбцов матрицы W_F. (5):

^w ? = ^(w 1 /^,w2/ , ° ^,w. / ..... ^wn _{j k}_^ V ⁵ = ^П/ _k _ i .                    ⁽⁶⁾

Любой элемент произвольного столбца матрицы можно вычислить по экспертным оценкам относительно критерия, принимаемого за базовый, которому соответствует единичный элемент        на главной диагонали матрицы.

Теорема 1 . Пусть даны экспертные оценки w /,/ _{+ 1} , 5 = 1,П/_к_₁ — 1, предпочтительности смежных подкритериев F / на k-м уровне, входящие в вершину F / на ( к — 1) -м уровне иерархии. Тогда любой элемент столбца матрицы V/ _F.    (4) может быть вычислен по эле-

Jk-l ментам оценок, расположенным над главной диагональю матрицы по формуле:

Гп/-ww+t+1, Л < V, V л = 1,5- 1, w. / = j 1      _V 7 = 5

[ ^(п? ^- / ^{1 w ;} ,t+1 )   , Л >  ^5V Л = ⁵ + ^1, n_{/ k}_₁ .

Доказательство . Действительно, для номеров строк л < 5 можно записать:

;    _ адЦ    wZ^-b1w

— II W —     X     X XX

? ^/       t -?   t ,t ⁺¹ wZ ^b 1    wZ, ,* 2          wZ ^_ 1

w?^-^ w Z^ wl^    wl^

аналогично для номеров строк л > 5 можно записать:

/ О \    ( ™Ц  wl_K+1    wl^

= I I w ;        =        X       X .„ X       X

, I      \wZ / ₊ 1 w/ /+2         wZ ? _ 1

wVi wl^

г=ет

wZ?

wZ/'

что и требовалось доказать.

Пример 1. Пусть для четырёх упорядоченных по важности f- v > f₂> ! з > f ^ критериев известны количественные веса wZ(f₁) = 4, wZ(f₂) = 3, wZ(/₃) = 2, wZ(/₄) = 1.

Их нормированные веса имеют значения 0,4; 0,3; 0,2 и 0,1. Пусть локальные веса заранее неизвестны, но эксперт результаты сравнения смежных пар представил в виде:

W12 ~ -; W2 3 « которые приняты за наддиагональные элементы матрицу можно представить в виде w = (

	/ *
3/4 *		/
	/ *
		/

∗

∗

0 0 2 *

3            2

-; ^W 34 ~ -, матрицы. С учётом обратной симметрии

)

Остальные элементы столбцов w_;³ = (w_1;; w_2/, w_3/,, w_4/)⁷,; = 1,4, матрицы вычисляются по формулам, в которые обязательно входят наддиагональные элементы:

1                         2*

W 1 ³: W 31 = W 32 W 21 = -

∗

∗

W 4 1 = W 4 з W 3 1 = -

W 2³:

• 2 =

1*

I

^W з-

W 42 = W 4 з W 3 ₂ = -

W 31 = W 23 W 12 = I

W ³

з

∙

1 :

2’

∙

∙

∙

∗

4*

4 =2:

∗

W 14 = W 1*2 W 2*3 W f4 = -

• ³ * • 2 * = 4; 2                ’

^W2 4 = ^w23^W34 = *

В результате получается матрица: w = (

∗

• 2 * = 3.

	/ *
/ *		/ *
/	/ *		*
/	/	/ *

)

Замечание 2. Можно убедиться, что ранг матрицы 1У (8) равен 1, и она является мультипликативной, например, для элемента матрицы (8) справедливо

Матрица W^.   (4) с вычисленными элементами по формуле w^$ (7) называется полной матрицей.

Шаг 4. Формирование локальных коэффициентов важности критериев. За локальные коэффициенты принимаются нормированные элементы любого столбца матрицы И/?.  , вы-

Jk-1 численные по формуле (7). Можно доказать, что нормированные элементы полной матрицы совпадают между собой и равны нормированным локальным весам критериев.

Теорема 2 (о взаимосвязи между нормированными элементами полной матрицы и нормированными весами критериев). Нормированные элементы столбцов W3 (6), 5 = 1,п;-к1, вычисленные по наддиагональным элементам по формуле w^$ (6) матрицы W^.   (4), сов падают между собой и равны нормированным весам критериев, т.е.

. / ^ \ ( ^\   ---

" 3 = (_ -   ) = ( ~-   ) v5 = ^1,п_Л .₁ ,

"Ч-Л   "Ч-/ где Wn$ =   л^— - нормированный элемент 5-го столбца W3;

∑

_~         IV/n wl^ = —------ нормированный вес F локального критерия. 2Л ^ 1 w ц

Доказательство. Из формулы (6) следует, что для полной матрицы для любого столбца w^ (5), ^ = Fn^ справедливо w^^ = ^, ] = 1, Пук_1

Откуда

" " ^: = к ". 1 w»    = е ". i W/ „ = ^w' -      =^{1 1}

что и требовалось доказать.

Если в примере 1 пронормировать столбцы матрицы W (8), то они совпадут между собой и будут равны нормированным весам критериев:

( 0,4 0,3 0,2

\ 0,1

)

Таким образом, за коэффициенты важности критериев можно взять нормированные элементы любого столбца, которые вычисляются по наддиагональным элементам матрицы попарных сравнений смежных критериев.

При решении прикладных задач проще использовать элементы последнего столбца матрицы, которые можно вычислить через произведения w^₊₁, ^ = 1, Пу_k_₁ — 1 экспертных оценок по формуле:

^w " j _k _ 1 = [

п^-1

^wt, t +1 , Т <  ⁿj _k_ 1 ,

Т = n< 1, а затем нормировать и принять за коэффициенты важности критериев.

Из примера 1 видно, что по формуле w„n.   легко вычисляются элементы столбца wl.

Шаг 5. Формирование глобальных коэффициентов важности критериев. Глобальные коэффициенты формируются путём вычисления произведения локальных коэффициентов вершин, лежащих на пути от корневой вершины F_o к произвольной концевой вершине.

Пусть веса wj j j .j_k нормированы, т.е. их сумма по всем подвершинам произвольной вершины Fi -j/c-i равна единице:

к^^-1 w ^j (F 1 *-/ J = ¹ V k = ГЯ

Произведение весов вершин, лежащих на пути от корневой вершины F 0 к произвольной концевой вершине f ₁j_2-j_n, будет представлять собой интегральный (глобальный) вес w g(f j ij_2-j_n) данной концевой вершины:

Тогда постановку многокритериальной задачи оценки объектов с многоуровневой структурой можно представить в виде аддитивной свёртки:

(D _ yn0  yn7 1    yn71 j2-7n             (D rz = 1A=1IA = 1- Ejn=1  ^j^.jn^-jn,         (9)

где jj (j) . = f ₁₇-_2-7п( a _z) - оценка a _z ЕЛ объекта в концевой вершине f ₁₇-_2-7п дерева ID в результирующей однородной шкале.

Решение задачи можно представить в виде упорядочения объектов в соответствии с зна- чениями агрегированных оценок:

a_q >  — > a_q ^ r^{(4 1 )} > — >  r?^nA\

^Q 1             ^Q n^      L              1

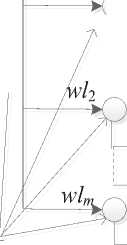
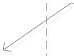
В качестве примера на рисунке 1 представлено трёхуровневое иерархическое дерево упорядоченных по важности критериев, где веса обозначены в виде:

wi^ = ^w^(^ji)’ A = 1, ^m ;

^wlkh = ^ld(/, J, A = 1X.

Замечание 3 . Глобальные коэффициенты, вычисляемые на шаге 5 данного метода, аналогично вычисляются и в методе ПАТТЕРН [2] и в МАИ [1]. При этом глобальный вес концевого критерия в иерархическом дереве характеризует (относительную) долю, которую он вносит в глобальный критерий верхнего (нулевого) уровня иерархии.

3 Анализ эффективности методов, базирующихся на матрицах парных сравнений

Номера уровней

F 0

wl 1

wl 1 n 1

F 2 wl ₂₁

Групповые критерии

F 1

Глобальные веса

Локальные веса

>O f .1 wg 11 = A ^x A\

...

^ ^f П1 wg 1 n₁ = A ^x w^l 1 n₁

^f 21 wg ₂₁ = wl 2 x wl ₂₁

wl 2 n ² ► f 2 n wg 2 n 2 = wl 2 ^x wl 2 n 2

F 3         ²

w^l m1 ¹—Ю f_m 1 ^wg_m 1 = wl_m^x wl „1 1

. . .

w mnm mn g

Концевые критерии     m

= mV x mV m nm      m     m nm

Рисунок 1 – Трёхуровневое иерархическое дерево критериев оценки объектов

Для сравнения методов используются данные из работы [19], в которой оцениваются сравнительные расстояния между городами Каир, Токио, Чикаго, Сан-Франциско, Лондон, Монреаль. Матрица парных сравнений получена методом экспертных оценок [19]:

/ 1   1/3   8     3     3   7\ /  3     1     9     3     3    9\ /8   /9         /6   / Л =  1/3  1/3   6    1   1/3  6 . /     /                      6 \1/7  1/9  1/2  1/6  1/6  1/

Упорядочив города в виде Токио, Каир, Лондон, Сан-Франциско, Чикаго, Монреаль по убыванию расстояния по методу данной работы, можно сравнить расстояния между смежными парами городов Токио-Каир, Каир-Лондон, Лондон-Сан-Франциско, Сан-Франциско-Чикаго, Чикаго-Монреаль, результаты которого можно представить наддиагональными элементами {1,2; 1,6; 1,5; 2,9; 1,2} мультипликативной матрицы WMKn и вычисленными элементами правого столбца:

/ 0   1   1,6   0    0 W7   — 00   1  1,5  0 ^МКП =  0  0   0   1  2,9 8 5,42 ,   / нормированные элементы которого принять за количественные веса расстояний и представить в виде вектора: wMKn = (0,342; 0,285; 0,178; 0,119; 0,041; 0,034).

Поскольку по нормированным элементам весов критериев восстанавливаются все элементы w ^ = — мультипликативной матрицы, то за критерий сравнения принимается матричный критерий близости восстановленной мультипликативной матрицы W к исходной матрице А в виде матричной I, -норма [20]:

d(A.W) = НА - Wil, = St 1У= 11^ - ^|.

Мультипликативная матрица обладает особым свойством – любой элемент можно представить через произведение пары других

Wtj = wikwkj, V i,j,k = 1,n, где w = —; w = 1, i, j = 1, n.

ji    Wtj

Можно показать взаимосвязь между нормированными элементами важности критериев и элементами восстановленной мультипликативной матрицы.

Теорема 3 . Между любыми элементами w^ мультипликативной матрицы W = [w ij ] V i, j = 1, n и любой парой компонент (w_i , W j ) вектора важности критериев w = (w , , .„, w j ..., w_n)^T , j = 1, n справедливо биективное отображение W ^ w^, ставящее каждому отношению W в однозначное соответствие элемент w^ матрицы W, и обратно w_i j ^ W ^- , при этом справедливо равенство :

W

w =   - , Vi, j = 1, n.

^ij      W i

Доказательство. Так как матрица W = [wi;-] мультипликативная, то если для любой пары чисел (wi, wj) из {w,,..., wn}, представленных в виде отношения W-, wj > 0, выполняется условие мультипликативности (11), то между любыми элементами матрицы W = [wi;-], wij = W-, существует взаимно однозначное отображение между элементами wij и W-.

j               Wi            W                                   Wi _ W_k   Wi      j

Действительно, если w_ik =   - и w_kj = ^- , то согласно (12): w_ikw_kj =   - x - = - = w_ij ,

W—           Wj                               W—  Wj   Wj т.е. для всех i, j, k = 1, n выполняется условие мультипликативности (11), что и требовалось доказать.

Представленный МКП нахождения весов по парным смежным (n — 1) сравнениям можно сравнить с МАИ [1], методом наименьших квадратов (МНК) [21] и методом аппроксимационной матрицы (МАМ) [22].

По МАИ решением служит нормированный собственной вектор матрицы А, соответствующий максимальному собственному значению. По МНК в качестве искомого вектора w принимается решение оптимизационной задачи [21]:

S’i=iS’j=i(aiLjwj — wi)2 ^ min при ограничениях £р=1 wl = 1 и wl > 0 для всех i = 1, n.

Эти методы трудоёмки, и для построения матрицы А необходимо проведение (n² — n)/2 попарных сравнений. В МАИ для числа объектов не менее пяти процедура нахождения собственных значений матрицы степеней превосходства важностей критериев или предпочтений альтернатив осуществляется с применением численных методов нахождения корней полинома, реализованных в [23]. По МАМ в качестве искомого вектора w принимается решение оптимизационной задачи [22]:

ZF= 1 Е у=1 (a ij - ^Wi^{) 2} ^ mm                              ⁽¹³⁾

( ^{W W}n )

где aj ■ = =щ-^— - нормированные элементы матрицы суждений А = [ а ij ], i , j = 1, и; ^

Wi = W^ - нормированный элемент ^-го столбца мультипликативной матрицы, совпада ющий с любым элементом нормированного столбца (см. теорему 2).

Исходные данные для сравнения методов представлены в таблице 1.

Таблица 1 – Нормализованные относительные расстояния

Город	1
	И/ ИР	W MAH	w MHK	wMAM	^MKH
1	2	3	4	5	6
Токио	0,361	0,397	0,459	0,389	0,342
Каир	0,278	0,263	0,221	0,255	0,285
Лондон	0,177	0,164	0,141	0,167	0,178
Сан-Франциско	0,132	0,116	0,107	0,126	0,119
Чикаго	0,032	0,033	0,036	0,036	0,041
Монреаль	0,019	0,027	0,036	0,028	0,034

В столбцах 2 – 6 таблицы 1 представлены нормализованные относительные расстояния, где в столбце 2 - истинные нормализованные относительные расстояния, w_HP; 3 - расстояния по МАИ, w_mah; 4 - расстояния по МНК, w_mhk; 5 - расстояния по МАМ, w_mam; 6 - расстояния по МКП, w_MKn. Данные в столбцах 2, 3 и 4 взяты из работы [19, с.188].

Результаты сравнений по критерию d(A, W) (10) близости к исходной матрице парных сравнений представлены в таблице 2.

Таблица 2 - Результаты сравнений по критерию d(A, W)

Метод	ИР	МАИ	МНК	МАМ	МКП
d(A ,W)	36,41	24,62	29,22	23,10	20,26

Эффективность методов можно оценить по критерию близости между векторами: ^d(wi^,W j) = Z k=1 | ^Wi ^{(k) — W}j ^{(k) |} -

Результаты сравнения представлены в таблице 3.

Таблица 3 - Результаты сравнений по критерию d(w _i , w j )

Метод	МАИ	МНК	МАМ	МКП
d(w HP , w j )	0,089	0,237	0,080	0,064

Таким образом, методы, базирующиеся на матрице парных сравнений, можно ранжировать по убыванию эффективности: MKH > MAM > MAH > MHK.

Замечание 4 . Преимущество МКП относительно методов, базирующихся на матрице парных сравнений, в том, что этап построения иерархического дерева упорядоченных критериев по убыванию важности позволяет снизить число экспертных смежных пар сравнений критериев до (и — 1) по сравнению с числом при парном сравнении (и² — и)/2.

4 Пример решения задачи многокритериального оценивания

Эффективность МКП можно рассмотреть на примере решения многокритериальной задачи сравнения боевых самолётов по тактико-техническим характеристикам (ТТХ), принимавших участие в индийском тендере MMRCA [24]. Исходные данные по девяти показателям в виде множества F = {/1, .„, /9} и оценки х(1) = /(Сг) шести самолётов в виде множества С = {Сг, .„, С6} представлены в таблице 4, где приняты обозначения самолётов: С - Dassault Rafale; С2 - Eurofighter Typhoon; С3 - F-16IN Super Viper; С4 - F/A-18E/F Super Hornet; С5 -JAS 39 NG (IN); С6 - МиГ-35. Эталонные самолёты обозначены: С* - наихудший по показателям ТТХ и стоимости (эталон - худший вариант); С* - наилучший по показателям ТТХ и стоимости (эталон - лучший вариант).

Таблица 4 - ТТХ самолётов, участвовавших в тендере

Показатели ТТХ	Оценки самолётов в исходных шкалах, х ( 1) = /(С ; )						Эталоны
	Ci	с?	С 3	С4	С.	С.	∗	∗
- боевая нагрузка, т	9,5	7,5	7,8	8,05	5,3	7,0	5,3	9,5
- управляемый вектор тяги	нет	нет	нет	нет	нет	есть	нет	есть
- скороподъёмность, м/с	305	315	254	228	255	330	228	330
- максимальная взлётная масса, т	24,5	23,5	21,8	29,9	14,3	23,5	14,3	29,9
- максимальное число Маха на высоте	1,80	2,25	2,00	1,80	2,00	2,25	1,80	2,25
- практический потолок, км	15,24	19,81	18,00	15,00	15,24	17,50	15,00	19,81
- стоимость, млн. $ (2011 г.)	124	120	50	55	48	45	124	45
- тяговооружённость	1,03	1,18	1,10	0,93	1,18	1,10	0,93	1,18
- масса топлива, т	4,70	5,00	3,37	6,78	3,36	4,80	3,36	6,78

В соответствии с шагом 1 алгоритма представленные в таблице 4 показатели используются как критерии. Пусть эксперты разбили критерии на три группы по предпочтительности: Р_г - целевая эффективность; Р₂ - техническая эффективность и Р₃ - технико-экономическая эффективность:

Р о : Р 1 > Р 2 > Р з -

В каждой группе подкритерии также упорядочены по убыванию важности:

^Р1^: / 11 > / 12 > / 13^{; Р}2 ^: / 2 1 > 7 22 > / 23^{; Р}3^: / 3 1 > Л 2 ~ / 33 "

На рисунке 2 представлено трёхуровневое иерархическое дерево.

В соответствии с шагами 2 и 3

представлены матрицы попарных

смежных сравнений и вычисленные

правые столбцы:

Р о : ^ 0 = (о V 0

Р 1 : W = ( 0

(

Р 3 : W 3 = (0

5/3

4/3

8/7

9/8

5/2\

³ 0 ² )'

/

)

8/6\

⁷ 0 ⁶ )'

9/8

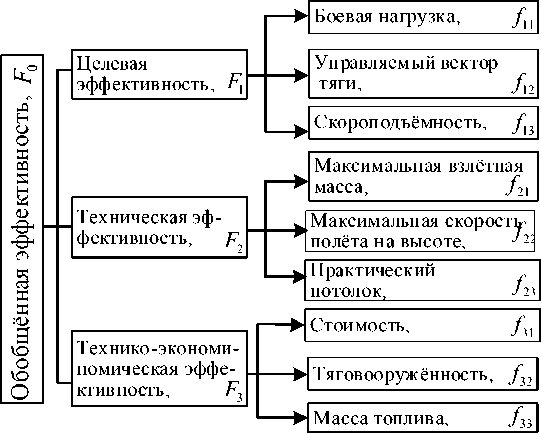
Рисунок 2 - Иерархическое дерево критериев оценки эффективности самолётов

)

В соответствии с шагом 4 сформированы локальные коэффициенты важности критериев:

F_o : wI ₁ = 0,5; w1 ₂ = 0,3; w1 ₃ = 0,2;

F_t : wI ₁ i = 0,4; wl_{1 2} = 0,3; wl_{1 3} = 0,3;

F₂ : w1₂ 1 = 0,38; w1 ₂₂ = 0,33; w1 ₂₃ = 0,29.

F₃ : wl ₃₁ = 0,36; wl₃₂ = 0,32; wl ₃₃ = 0,32.

Глобальные коэффициенты важности критериев на шаге 5 формируются путём вычисления произведения локальных коэффициентов вершин, лежащих на пути от корневой вершины к произвольной концевой вершине.

Fi : wg₁₁ = 0,5 x 0,40 = 0,20; wg ₁₂ = 0,5 x 0,3 = 0,15; wg_T3 = 0,5 x 0,3 = 0,15;

F₂: wg_{2 1} = 0,3 x 0,38 = 0,114; wg₂₂ = 0,3 x 0,33 = 0,099; wg₂₃ = 0,3 x 0,29 = 0,087.

F₃ : wg_{3 1} = 0,2 x 0,36 = 0,072; wg₃₂ = 0,2 x 0,32 = 0,064; wg₃₃ = 0,2 x 0,32 = 0,064.

Поскольку исходные данные представлены в различных шкалах измерения, то для при менения аддитивного механизма агрегирования необходимо перейти к результирующей однородной шкале [19]. Правило перехода пt от исходных оценок х() самолётов в количественной шкале по ft критерию к г^ оценкам в результирующей балльной шкале можно представить в виде множественно-точечного отображения:

• 74 : [ft ■* + (г - 1)h_z, ft* + г^] — г,

*

где h_z (m) = ^{1  1} * — шаг дискретизации шкалы ft критерия, ft * - минимальное значение,

• ^∗– максимальное значение критерия;

X_t , _г = [х г _-1, х г ] = [ft ’* + (г — 1)h t , ft * + г^ ] - отрезки разбиения исходной шкалы;

• г Е R = {1,2,..., b } - градации результирующей шкалы;

• b - число шкальных градаций в порядковой (балльной) шкале.

При этом каждой оценке, попадающей в класс ^ , _г разбиения ставится в соответствие оценка г] ^Z) в результирующей шкале по правилу: х® — г]^г). В случае попадания оценки объекта на смежные классы ей присваивается связанный ранг, равный среднему арифметическому значению смежных рангов [25]: х® — г^(Z) = ^^(гт , если х® е x_ir ПХ_z , _r+1.

В качестве механизма агрегирования оценок самолётов, представленных в результирующей шкале, применён интегральный метод с учётом весов и без учёта в виде аддитивной свёртки оценок a_q , q = 1^6, по концевым критериям с весами важности в виде [26]:

F ⁽ a z ; wg 1 ,..., wg_m) = S> 1 wg^)^¹ ) ,                         (14)

где ft® = ft(aZ) - оценка самолёта aZ Е Д = {aZ|l = 1,пл},пл = 6 в результирующей шкале по критерию ft, i = 1, m, m = 9; wgt = wg(ft) - глобальный вес ftt критерия.

В таблице 5 представлены ТТХ самолётов в 100-балльной результирующей шкале, где i²_Z = (г^, г ₂® , ., г_i^(Z), ., г^ ) ) - профиль C_Z самолёта, l = 1^9., а также результат агрегирования без учёта весов критериев (в последней строке таблицы).

Ранжирование самолётов по обобщённым оценкам без учёта весов критериев можно представить в виде:

Eurofighter)   ( F — 16 IN 1   fF/A 18E/F —)   rDassauln . (JAS 39 )

Typhoon J   (Super Viper]   (Super Hornet]   (Rafale]   (NG (IN)]"

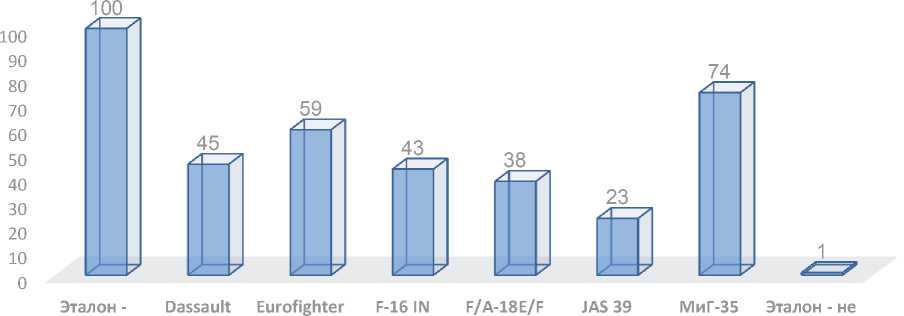
Результаты агрегирования с учётом глобальных весов по формуле (14) представлены в таблице 6, а также на рисунке 3.

Таблица 5 - Оценки самолётов в однородной 100-балльной шкале без учёта весов критериев

Показатели	Оценки самолётов в однородной 100-балльной шкале, ( т=^Ъ						Эталоны
	⃗	⃗	⃗	⃗	⃗	⃗	⃗∗	⃗∗
≡	100	53	60	66	1	41	1	100
≡	1	1	1	1	1	100	1	100
≡	76	86	26	1	27	100	1	100
≡	66	59	49	100	1	59	1	100
≡	1	100	45	1	45	100	1	100
≡	5	100	63	1	5	52	1	100
≡	1	6	94	88	97	100	1	100
≡	40	100	68,5	1	100	68,5	1	100
≡	40	48	1,0	100	1	43	1	100
( ) = Z L ^	330,0	553,0	407,5	359,0	278,0	663,5	9	900

Таблица 6 - Показатели самолётов в результирующей шкале с учётом весов критериев

Показатели	Глобальные веса критриев	Оценки самолётов в однородной 100-балльной шкале с учётом весов						Эталоны
		Ci	c2	C3	C4	c5	c6	∗	∗
≡	0,200	20,00	10,60	12,00	13,20	0,20	8,20	0,20	20,00
≡	0,150	0,15	0,15	0,15	0,15	0,15	15,00	0,15	15,00
≡	0,150	11,40	12,90	3,90	0,15	4,05	15,00	0,15	15,00
≡	0,114	7,52	6,73	5,59	11,40	0,11	6,73	0,11	11,40
≡	0,099	0,10	9,90	4,46	0,10	4,46	9,90	0,10	9,90
≡	0,087	0,44	8,70	5,48	0,09	0,44	4,52	0,09	8,70
≡	0,072	0,07	0,43	6,77	6,34	6,98	7,20	0,07	7,20
≡	0,064	2,56	6,40	4,38	0,06	6,40	4,38	0,06	6,40
≡	0,064	2,56	3,07	0,06	6,40	0,06	2,75	0,06	6,40
Z г wg (P		44,80	58,88	42,79	37,89	22,85	73,69	1,00	100,00

NG(IN)

идеал идеал

Rafale     Typhoon Super Viper Super

Hornet

Рисунок 3 – Результат оценивания самолётов в 100-балльной шкале с учётом весов критериев

В этом случае ранжирование самолётов по обобщённым оценкам с учётом весов критериев можно представить в виде:

{МиГ- 35} > [Eurfghterj > {Dassault} >{ p oon

F - 16 IN ' p ip

) f F/A 18E/F— 1 MAS 39 1 p o n

На первом месте оказался самолёт МиГ-35 так как по трём показателям у него максимальные баллы. Кроме того, преимущество самолёта связано с наличием управляемого вектора тяги, который отсутствует у других самолётов.

По результатам агрегирования рейтинг боевых самолётов по эффективности представлен в таблице 7. Таким образом, самолёт МиГ-35 оказался лучшим по ТТХ и по стоимости.

Таблица 7 - Рейтинг самолётов по эффективности

№	Самолёт	Балльная оценка		Место в рейтинге
		Без учёта весов	С учётом весов	Без учёта весов	С учётом весов
1	Dassault Rafale	37	45	5	3
2	Eurofighter Typhoon	60	58	2	2
3	F-16 IN Super Viper	45	43	3	4
4	F/A 18E/F — Super Hornet	40	38	4	5
5	JAS 39 NG(IN)	31	23	6	6
6	МиГ-35	63	59	1	1

Заключение

Основное преимущество предложенного МКП - в его простоте относительно МНК и МАИ, в отсутствии выполнения всех попарных сравнений, число которых нелинейно зависит от исходного числа объектов и равно ( n 2 -n )/2. Снижение числа сравнений смежных пар критериев до значения ( n- 1) достигнуто за счёт предварительного упорядочения критериев по важности (предпочтительности) и особых свойств матрицы с наддиагональными экспертными оценками критериев, измеренных в шкале отношений.

Предложенный метод формирования весов критериев для многокритериальных задачах с многоуровневой структурой может быть использован для решения задач оценивания, ранжирования и построения рейтингов.