Метод локального измерения толщины тонких металлоизделий с помощью ультразвука

Одним из практических применений в ультразвуковой дефектоскопии волн Лэмба является измерение толщины тонких металлических изделий (пластин, листов, лент, оболочек и т. п.). Особенно актуален этот вопрос в случаях, когда изделия являются крупногабаритными, а также, когда измерения возможны только при одностороннем доступе к изделию [1-3].

Методика проведения исследований

Скорость распространения волн Лэмба в изделии определяется его толщиной и частотой акустических колебаний [3, 4]. Количественную связь между этими параметрами можно установить, если проанализировать дисперсионные кривые - зависимости групповых скоростей волн Лэмба от толщины изделия и частоты колебаний. В этом случае задача измерения толщины листовых металлоизделий сводится к экспериментальному измерению скорости волн Лэмба и частоты акустических колебаний в них. В работе [5] предложен способ локального измерения групповой скорости волн Лэмба, возбуждаемых термоакустическим излучателем (ТА-излучателем) с постоянной мощностью теплового излучения. Было установлено, что с увеличением диаметра ТА-излучателя форма возбуждаемого ультразвукового импульса изменяется, происходит его разделение на два импульса, причем источниками разделенных акустических импульсов являются противоположные края ТА-излучателя, где имеет место градиент температуры металла. Время отставания этих импульсов относительно друг друга определяется диаметром ТА-излучателя и скоростью распространения ультразвука. Тогда скорость волн Лэмба на участке изделия, длина которого не превышает диаметра ТА-излучателя (лазерного луча), можно рассчитать по формуле и = 5 / At, где S – расстояние между краями ТА-излучателя (его диаметр), ∆t – время прохождения ультразвуком этого расстояния.

В качестве примера определим по предложенной методике толщину шлифованной пластинки инварного сплава размерами 270 × 60 × 0,60 мм. Толщина пластинки измерялась стандартным микрометром. На рис. 1 приведена экспериментальная осциллограмма у.з. импульса волны Лэмба. Диаметр ТА-излучателя 9,7 мм, средняя мощность теплового излучения Р = 2,8 Вт. Регистрируются волны Лэмба широкополосным ЭМА-приемником [6].

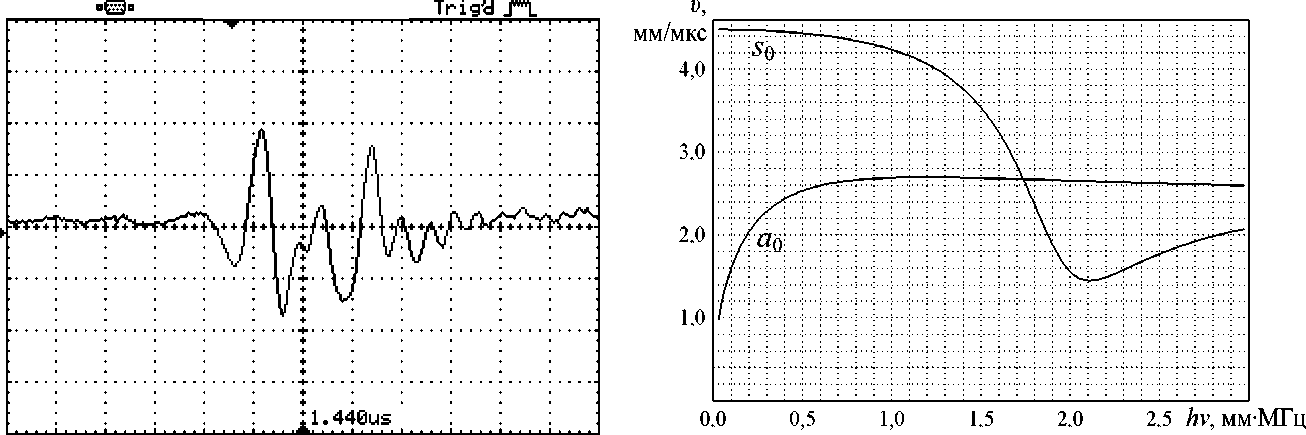
Рис. 2. График дисперсионных кривых групповых скоростей симметричных и антисимметричных волн Лэмба нулевой, первой и второй мод

MAIN           Mius T EDGE I

CHI — 5U     CH2 — 500mU

Рис. 1. Импульс у.з. волны Лэмба от ТА-излучателя диаметром 9,7 мм

Из осциллограммы следует, что среднее время 〈∆ t 〉 = 2,2 мкс, средняя частота колебаний 〈 ν 〉 = 0,85 Мгц. Тогда средняя групповая скорость у.з. волн Лэмба

9,7       мм

〈 υ 〉 =    = 4,41 (    ) .

2,2       мкс

Расчеты зависимости групповых скоростей волн Лэмба от толщины пластинки и частоты (дисперсионные кривые) выполнялись по формулам, взятым из [3]. Скорости поперечных и продольных волн, входящие в эти формулы, были соответственно равны 2683 и 4878 мм/мкс [7]. Результаты расчетов симметричных и антисимметричных волн Лэмба трех низших номеров представлены в виде графика υ = f ( h ⋅ ν ) на рис. 2.

Из графика следует, что экспериментально измеренная групповая скорость соответствует симметричной волне Лэмба нулевой моды. Из точки дисперсионной кривой, соответствующей этой скорости, опускаем нормаль на ось h ν и находим численное значение параметра k = h ν = 0,53 мм·МГц. После этого рассчитываем среднюю толщину пластинки

〈 h 〉 = 0,53 = 0,63 мм.

0,85

Оценим погрешность полученного результата [8]. Расчетной формулой является выражение h = k / ν . Считаем, что погрешность параметра k определяется погрешностью измерения скорости υ волн Лэмба. Систематическая относительная погрешность при косвенных многократных измерениях толщины пластинки определяется в основном максимальной погрешностью цифрового осциллографа и равна 1,4 %. С лучайная относительная погрешность, которую рассчитываем с помощью доверительного интервала, составляет 4,2 %. Величина доверительной границы суммарной погрешности σ _h равна 4,4 %. В результате получаем:

h = 0,63 ± 0,03 мм , σ _h = 4,4%.

Определим толщину этой же пластины путем многократных прямых измерений стандартным микрометром. С истематическая погрешность прибора – 0,7 %. Случайная погрешность рассчитывается с помощью доверительного интервала и составляет 1,7 %. Величина доверительной границы суммарной погрешности σ _h * равна 1,8 %. В результате получаем:

h ^* = 0,60 ± 0,01 мм, σ _h ^* = 1,8% .

Физика

Выводы

• 1.    Используя зависимость скорости волн Лэмба от толщины изделия и частоты акустических колебаний, предложен метод измерения толщины тонких металлоизделий.

• 2.    Скорость и частота колебаний определялись экспериментально при генерации волн Лэмба в тонких металлических изделиях с помощью лазерных импульсов наносекундной длительности. Длина участка изделия, на котором измерялась скорость, не превышает толщины лазерного луча.

• 3.    Проведена оценка погрешностей измерения толщины. Если нижняя граница относительной погрешности допускается равной или больше 5 %, то предложенный метод измерения является весьма перспективным, особенно когда объекты контроля имеют значительные габариты и доступ к измерениям является односторонним.

Статья выполнена при поддержке Правительства РФ   (Постановление

№ 211 от 16. 03. 2013 г.), соглашение № 02. АО3. 21. 0011.