Метод многосеточных конечных элементов в расчетах трехмерных композитных пластин и балок сложной формы

Введение. При анализе напряженного состояния композитных пластин и балок сложной формы широко используют микро- и макроподходы. Реализация макроподхода для композитных пластин и балок регулярной структуры сводится к проблеме нахождения эффективных модулей упругости, которая особенно трудно решаема для композитов нерегулярной структуры [1]. Расчет композитных пластин и балок сложной формы по методу конечных элементов (МКЭ) с применением уравнений трехмерной теории упругости приводит к построению базовых дискретных моделей высокой размерности, порядка 108 v 1010 . Ширина ленты системы уравнений МКЭ для таких базовых моделей равна 105 v 106 [2-4]. Применение в этом случае программ расчета ANSYS, NASTRAN и других затруднительно. В основе построения приближенных (технических) теорий деформирования упругих композитных пластин и балок лежат гипотезы [5–8], которые порождают решения с неустранимой погрешностью.

Цель исследований : анализ напряженного состояния упругих трехмерных композитных пластин и балок сложной формы с различными коэффициентами наполнения при статическом нагружении.

Методы и результаты исследования . Предложен метод многосеточных конечных элементов [9, 10], краткая суть которого состоит в следующем. Предлагаемый метод реализуется на основе алгоритмов МКЭ с применением трехмерных однородных и композитных многосеточных конечных элементов (МнКЭ). Отличия МнКЭ от существующих КЭ состоят в том, что в МнКЭ учитывается (в рамках микроподхода [1]) сложная неоднородная структура и форма и описывается напряженное состояние уравнениями трехмерной теории упругости без введения дополнительных упрощающих гипотез. При построении МнКЭ [11–14] используем функции перемещений в виде степенных и лагранжевых полиномов различных порядков и уравнения трехмерной задачи теории упругости [4], записанные в локальных декартовых системах координат. Полиномы Лагранжа эффективно применяются при построении МнКЭ пластинчатого и балочного типов. Показаны процедуры построения МнКЭ формы прямоугольного параллелепипеда и сложной формы. Достоинства предлагаемых МнКЭ состоят том, что они:

– учитывают неоднородную структуру и сложную форму пластин и балок;

– образуют многосеточные дискретные модели, размерность которых в 1 0 3 v 10 5 раз меньше размерностей базовых моделей пластин и балок;

– порождают приближенные решения с малой погрешностью.

Реализация МКЭ для многосеточных дискретных моделей требует в 10 3 v 10 5 раз меньше объема памяти ЭВМ, чем для базовых моделей.

Следует отметить, что метод многосеточных конечных элементов (ММнКЭ) является более глобальным, чем МКЭ. Во-первых, ММнКЭ всегда можно использовать при решении всех краевых задач, которые решаются с помощью МКЭ (поскольку вместо односеточных КЭ всегда можно использовать МнКЭ, которые порождают дискретные модели малой размерности). Во-вторых, в МКЭ используются только однородные односеточные КЭ, а в ММнКЭ можно использовать как однородные, так и неоднородные МнКЭ, что позволяет эффективно учитывать неоднородную структуру тел. В-третьих, расчет ряд конструкций сложной формы с неоднородной (микронеоднородной) структурой по МКЭ в рамках микроподхода связан с большими трудностями или невозможен для существующих ЭВМ, а расчет с помощью ММнКЭ возможен (см. пример расчета композитной пластины в работе [9]).

1. Процедура построения двухсеточных КЭ сложной формы. Основные положения процедуры покажем на примере построения композитного 2-сеточного КЭ (2сКЭ) V“ сложной формы балочного типа. 2сКЭ Vna формы прямоугольного параллелепипеда размерами 18h х 24h х18h , имеющий отверстие сложной формы, расположен в локальной декартовой системе координат Oxyz (рис. 1). Считаем, что между компонентами неоднородной структуры 2сКЭ V связи идеальны. Пусть 2сКЭ Vna арми- рован непрерывными волокнами, параллельными оси Oy. Область 2сКЭ V^ представляем базовым разбиением R , состоящим из однородных односеточных КЭ (1сКЭ) Ve 1-го порядка формы куба со стороной h, e = 1,...,M; где M - общее число 1сКЭ. На рисунке 1 показано базовое разбиение 2сКЭ V^ на 1 сКЭ Ve в плоскости Oxz, сечения волокон (размерами h х h) закрашены. Функции перемещений, напряжений и деформаций компонентов удовлетворяют закону Гука и соотношениям Коши, отвечающим трехмерной задаче теории упругости [4], т. е. во всей области 1сКЭ, следовательно, и в 2сКЭ V реализуется трехмерное напряженное состояние. Базовое разбиение Ra учитывает неоднородную структуру и сложную форму 2сКЭ Va и порождает мелкую узловую сетку h . На мелкой сетке ha определяем крупную сетку На, узлы которой на рисунке 2 отмечены точками. Общее число узлов крупной сетки На равно 60. Крупная сетка H вложена в прямоугольную сетку n х п2 х n , которая расположена в целочисленной системе координат i, j,k ; i = 1,...,n, j = 1,...,n2, k = 1,...,n3, для рисунке 2 имеем n1 = 4 , п 2 = 5 , п3 = 4.

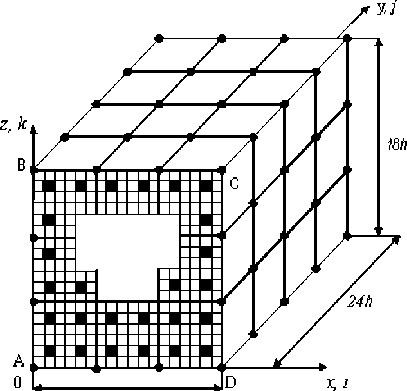
18И

Рис. 1. 2сКЭ V^a сложной формы

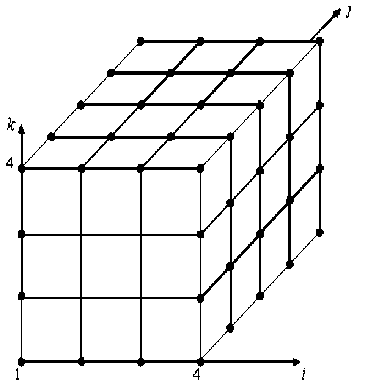
Рис. 2. Сетка H

При построении базисных функций перемещений Vij_k ( x , У , z ) 2сКЭ V„ используем полиномы Лагранжа L ( y ) и двумерный интерполяционный полином р ( x, z) . Общее число функций р_9к равно 60. Основание 2сКЭ V , которое лежит в плоскости Oxz и имеет 12 узлов крупной сетки, рассматриваем квадратным КЭ ABCD 3-го порядка с отверстием (см. рис. 1). Для аппроксимации перемещений КЭ ABCD используем полином P_a ( x , z ) вида

P_a ( x, z ) = a_x + a^x + a₃z + a^xz + a₅x ² +

+ a₆z ² + a₃x ² z + a^xz ² +

3            3           3           3

+ a₉xz + a₁₀zx + a_nx + a_nz ,          (1)

где a, - постоянные, i = 1,...Д2 .

Базисную функцию y/_ffk ( x , y , z ) для узла i , j , k крупной сетки H_a 2сКЭ V a с координатами x , y , z представляем в следующей форме:

W ijk ^{( x} , У , ^z ) = N ik ^{( x} , ^z ) ^L j ⁽ У ) , ⁽²⁾

где N ( x , z ) - базисные функции перемещений КЭ ABCD (см. рис. 1), которые отвечают полиному P_a ( x , z ) вида (1), i = 1,...,4 , j = 1,...,5 , k = 1,...,4 ; L .( у ) - полином Лагранжа 4-го порядка [2]:

L j ( У ) = П         ' .             (3)

а 1, а< j y j ^- У а

Для каждого узла i , j , k крупной сетки H_a 2сКЭ V_n^a определим число в и введем обозначение N = ^_к , в = 1,...,60 . Тогда функции перемещений u , v , w 2сКЭ V ^a (построенные на крупной сетке H ) представим в форме

60                   60                  60/м ua =Х Neue , va =S Ne vfi , wa =S Nв Wв , в=1                     в=1

где N , u , v , w - базисная функция и перемещения в -го узла сетки Н_а.

Обозначим:

q П = { U 1 ,...,u 60 , V 1 ,..., v 60 , W 1 ,..., w ®/ — вектор узловых перемещений сетки H , т. е. вектор узловых перемещений 2сКЭ V^a . Полную потенциальную энергию П^a базового разбиения R 2сКЭ V ^a представим в виде

M nn = £ (т qT [ K'h ]q e - qTPe),     (5)

e = 1  ²

где [Kh] - матрица жесткости; Pe,qe - векто ры узловых сил и перемещений 1сКЭ V .

Используя (4), вектор q узловых перемещений 1сКЭ V выражаем через вектор qa узловых перемещений 2сКЭ V a . В результате получим равенство qe = [Aaa ] q",                 (6)

где   [ A^ ]    - прямоугольная матрица, e = 1,..., M.

Подставляя (6) в выражение (5), из условия дП_п a / d q a = 0 получаем матричное соотношение [ K a ] q a = F a^a , отвечающее равновесному состоянию 2сКЭ V^a :

M M

[ K a ] = D A a ] T [ K ][ A e ] , F a = Z ^[ A^a a ^] P e , (7) e = 1                                        e = 1

где [ K^a a ] , F a - матрица жесткости и вектор узловых сил 2сКЭ V^a .

Порядок n 2сКЭ V_n^a при p = n = n = n равен n_a = p - 1 .

Замечание 1. В силу (6) размерность вектора q ^a (т. е. размерность 2сКЭ V ^a ) не зависит от числа M , т. е. от размерности разбиения R_a . Поэтому для учета сложной неоднородной структуры и формы, сложного характера нагружения 2сКЭ V ^a можно использовать сколь угодно мелкие базовые разбиения R , состоящие из 1сКЭ V . В этом случае в 1сКЭ V , следовательно, и в 2сКЭ V^a сколь угодно точно описывается трехмерное напряженное состояние [4].

Замечание 2. Решение, построенное для сетки H 2сКЭ V ^a , с помощью формулы (6) проецируем на мелкую сетку h базового разбиения 2сКЭ V^a , что дает возможность вычислять напряжения в любом 1сКЭ V базового разбиения 2сКЭ V^a , т. е. определять напряжения в любом компоненте неоднородной структуры пластин и балок.

Замечание 3. При построении 2сКЭ пластинчатого (балочного) типа используем полиномы

Лагранжа, имеющие по осям Ox , Oy (по оси Oy ) более высокий порядок аппроксимаций, чем по оси Oz (по осям Oz , Ox ), т. е. " , n ₂ >  n ₃ ( n₂ >  " , n₃ ). Достаточно мелкие разбиения композитных пластин, балок представляются однородными 2сКЭ. При проектировании однородных 2сКЭ используется процедура, аналогичная п. 1.

• 2.    Процедура построения n- сеточных КЭ. Рассмотрим процедуру построения n -сеточного КЭ Vⁿ формы прямоугольного параллелепипеда, ⁿ ^ ² [14]. Область КЭ V" состоит из ( n - 1 )-сеточных КЭ Vin ^{- 1} , i = 1,..., M_n__p M_n__l - общее число КЭ V" ^{- 1} . При этом КЭ V" ^{- 1} имеют одинаковые геометрические размеры, крупные сетки, неоднородную структуру и базовые разбиения. Крупные сетки КЭ V" ^{- 1} ( i = 1,..., M_n_ J образуют сетку h , на которой определяем крупную H сетку для КЭ V ⁿ (сетка H вложена в сетку h ). Функции перемещений u_n , v_n , w_n n -сеточного КЭ H , построенные на крупной сетке H с помощью полиномов Лагранжа (степенных полиномов), запишем в форме

m о                        m 0                        m о u. =D N'e «в •   v.=X Ne q’, •   w.=X N'e «в, (8)

в =1                       в =1                        в =1

где N ⁿ – базисная функция β -го узла сетки H ; q^u u , q v , q w - значения соответственно функций u_n , ^v _n , ^w _n в в —м узле сетки H_n ; m₀ - общее число узлов сетки H .

Полную потенциальную энергию Пⁿ n -сеточного КЭ Vⁿ представляем как сумму полных потенциальных энергий ( " - 1) -сеточных КЭ V" ^{- 1} , т. е. имеем

Mn-11

па = £{r(q"-’) T [ K-1]q"-' - (qn-1) T Pi"-'}, i=1

где [ K " ^{- 1}] , p " ^{- 1} - матрица жесткости и вектор узловых сил КЭ V " ^{- 1} ; q_z " ^{- 1} - вектор узловых перемещений V" ^{- 1} .

Обозначим через q n_a вектор узловых перемещений крупной сетки V n КЭ V ” .

Используя (8), вектор q;’-1 выражаем через вектор qna. В результате получим q”-1 = [ Ai ] q:,              (10)

где   [ A ]    - прямоугольная матрица, i = 1,..., Mn—1.

Подставляя (10) в (9), из условия д П n / d q n = 0 получаем матричное соотношение вида [ Ki ] q nn = P i :

[ K i ] = S [ A ] T [ K i ^{- 1}][ A ] ’ P an = Z [ A n ] ^T P in ^{- 1} , ⁽¹¹⁾ i =1                                                      i =1

где [ K i ] , P n - матрица жесткости и вектор узловых сил n -сеточного КЭ V ” .

Замечание 4. Построение матрицы жесткости и вектора узловых сил n-сеточного КЭ V” проводится по единой процедуре (по единым формулам (11)) с применением матриц [ Kn-1], Pin-1 (n - 1)-сеточных КЭ V”-1 (i = 1,..., Mn_ J и матриц [An], [An]T, построенных с помощью функций перемещений (8) n-сеточного КЭ V”. Отметим, что n-сеточные КЭ V” порождают дискретные модели композитных пластин, балок меньшей размерности, чем ( n -1 )-сеточные КЭ V”-1.

• 3.    Многосеточные КЭ формы прямой призмы с основанием сложной формы. Рассмотрим 2сКЭ V_b неоднородной структуры формы прямой треугольной призмы с отверстием. Процедура построения 2сКЭ V аналогична процедуре п. 1. На рисунке 3 показаны мелкая и крупная сетки 2сКЭ V формы прямой треугольной призмы. Узлы крупной сетки 2сКЭ V_b отмечены точками (24 узла), сечение отверстия (ось которого параллельна оси Oy ) закрашено. Основание 2сКЭ V , которое лежит в плоскости Oxz и имеет 6 узлов крупной сетки, рассматриваем треугольным КЭ 2-го порядка с отверстием (см. рис. 3). Для аппроксимации перемещений треугольного КЭ используем полином вида

P ( x , z ) = a_v + a₂x + a₃z + a₄xz + a₅x ² + a₆z ² , a_t = const .

В формуле (2) для 2сКЭ V_b используется полином Лагранжа L_t ( у ) 3-го порядка, j = 1,...,4 . На рисунке 4 показан 2сКЭ V формы прямой призмы с трапециевидным основанием.

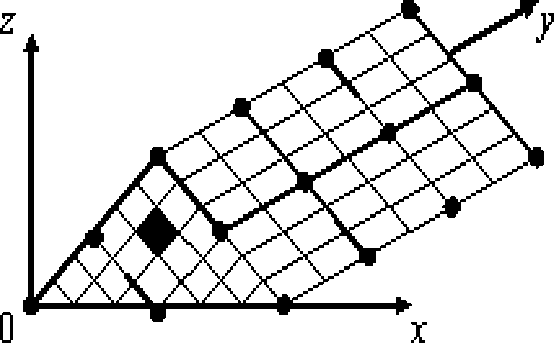
Рис. 3. 2сКЭ V

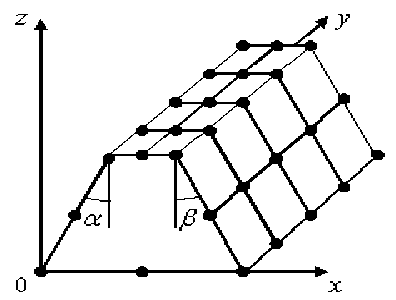
Рис. 4. 2сКЭ V

Узлы крупной сетки 2сКЭ V отмечены точками (40 узлов), считаем, что углы а , в малы. Основание 2сКЭ V , которое лежит в плоскости Oxz и имеет 8 узлов крупной сетки, рассматриваем КЭ 2-го порядка формы трапеции (см. рис. 4), для аппроксимации перемещений которого используем полином р ( x, z ) вида

P_d ( x , z ) = a_x + a₂x + a₃z + a₄xz + + a₅x ² + a₆z ² + a₇x² z + a^xz ²

В формуле (2) для 2сКЭ V полином Лагранжа L ( y ) имеет 4-й порядок, j = 1,...,5 . Рассмотрим 2сКЭ V сложной формы, показанный на рисунке 5. Боковая поверхность 2сКЭ V состоит из цилиндрической поверхности (образующая которой перпендикулярна к основаниям 2сКЭ V ) и граней в форме прямоугольников (ребра которых перпендикулярны к основаниям 2сКЭ V q ).

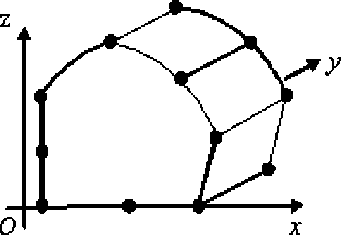
Рис. 5. 2сКЭ V

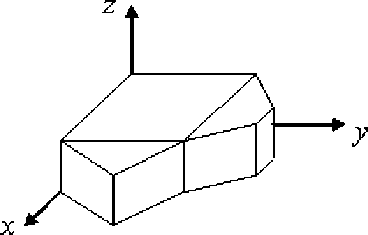
Рис. 6. Пластинчатый 2сКЭ V

Узлы крупной сетки 2сКЭ V_q на рисунке 5 отмечены точками (16 узлов). Основание 2сКЭ V , которое лежит в плоскости Oxz и имеет 8 узлов крупной сетки, рассматриваем криволинейным КЭ V 2 2-го порядка (см. рис. 5). Для аппроксимации перемещений криволинейного КЭ V 2 используем полином вида (12). В формуле (2) применяем полиномы Лагранжа 1го порядка, j = 1,2 . С помощью 2сКЭ V_b ( V_d , V ) по процедуре, аналогичной п. 2, проектируем трехсеточный КЭ ( n -сеточный КЭ, n >  2 , [14]) сложной формы.

Замечание 5. При использовании мелких разбиений композитные тела представляются однородными МнКЭ. Расчеты показывают, что МнКЭ n -го порядка (n = 1,2,3) формы прямоугольного параллелепипеда (треугольника, прямоугольника), спроектированные с применением мелких разбиений, для однородных тел порождают решения, совпадающие с решениями, построенными с применением однородных односеточных КЭ n -го порядка формы прямоугольного параллелепипеда (треугольника, прямоугольника) таких же размеров, как МнКЭ, узловые сетки которых совпадают с крупными сетками МнКЭ. Как известно [1–3], однородные известные односеточные КЭ n-го порядка порождают решения, которые сходятся в пределе к точным. Следовательно, решения, построенные для неоднородных тел с применением однородных и композитных МнКЭ n-го порядка формы прямоугольного параллелепипеда (треугольника, прямоугольника), в пределе сходятся к точным.

• 4.    Пластинчатые двухсеточные КЭ сложной формы. Пластинчатые 2сКЭ сложной формы можно рассматривать как гибридные, состоящие из 2сКЭ более простой формы. Пластинчатый 2сКЭ V сложной формы (рис. 6) состоит из следующих 2сКЭ, имеющих более простую форму: формы прямоугольного параллелепипеда, прямой треугольной призмы и прямой призмы, в основании которой лежит трапеция. С помощью 2сКЭ, из которых состоит гибридный 2сКЭ V_p , по процедуре, аналогичной п. 2, проектируем 3-сеточный пластинчатый КЭ ( n -сеточный КЭ, n >  2 , [2]) сложной формы.

• 5.    Результаты численных экспериментов. В качестве модельной задачи рассмотрим расчет балки V сложной формы волокнистой структуры (рис. 7). Балка V расположена в глобальной декартовой системе координат Oxyz , при у = 0 : u = v = w = о , т. е. балка жестко закреплена. Волокна параллельны оси Оу .

  

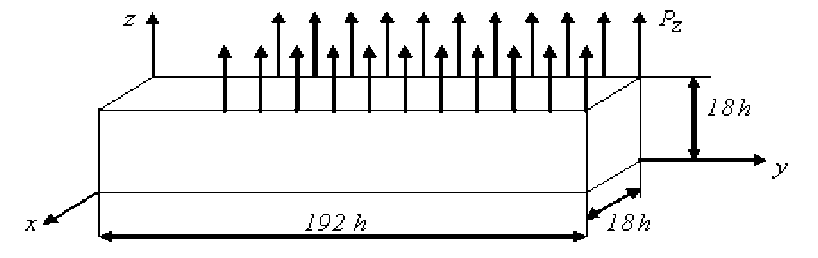
  Рис. 7. Композитная балка V

  
  

Базовое разбиение Ro балки состоит из однородных КЭ Vj 1-го порядка формы куба со стороной h=0.5, учитывает неоднородную структуру балки, сложную форму и порождает мелкую сетку ha размерности 19*193*19. Двухсе точная модель Rh балки состоит из 2сКЭ V размерами 18h х 24h х18h (см. рис. 1), построенными по процедуре п. 1, n = 1,...,N, N - общее число 2сКЭ Va, N = 8. Модуль Юнга связующего материала равен 1, волокон - 10, ко- эффициент Пуассона для волокон и связующего материала равен 0,3. Длина балки L = 192h , поперечное сечение балки размерами 18h х18h имеет отверстие сложной формы (см. рис. 1). В узлах сетки ha с координатами xi , у;, z = 18 h, где x; = 18h(а -1) , а = 1,2 , у. = 12h + 6h(в-1) , в = 1,-31 , на балку действуют вертикальные силы Pz = 0,015 , которые схематично показаны на рисунке 7.

Анализ результатов расчета балки показывает, что максимальные эквивалентные напряжения двухсеточной a h = 1,828 и базовой - а₀ = 1,969 моделей балки отличаются на 7,16 %. Максимальные перемещения двухсеточной w_h = 112,301 и базовой - w ₀ = 114,463 моделей отличаются 1,86 %. Размерность модели R балки равна 178 560, ширина ленты системы уравнений (СУ) МКЭ – 1985. Двухсеточная модель R _h балки имеет 1152 неизвестных (т. е. имеет в 155 раз меньше неизвестных базовой модели), ширина ленты СУ МКЭ равна 359 (в 5,5 раз меньше ширины ленты СУ МКЭ базовой модели). Реализация МКЭ для модели R требует в 855 раз меньше объема памяти ЭВМ и в 120 раз меньше временных затрат, чем для модели R ₀ . Эквивалентные напряжения определяем по 4-й теории прочности.

Выводы

В данной статье предложен метод многосеточных конечных элементов для расчета упругих трехмерных композитных пластин и балок сложной формы при статическом нагружении. Предлагаемый метод реализуется на основе соотношений и алгоритмов метода конечных элементов (в форме метода Ритца) с применением трехмерных однородных и композитных многосеточных конечных элементов.

Достоинства многосеточных конечных элементов состоят в том, что они учитывают в рамках микроподхода неоднородную и микронеод-нородную структуру, сложную форму пластин и балок, порождают дискретные модели малой размерности и численные решения с малой погрешностью.