Метод негладких интегральных направляющих функций в задаче о существовании периодических решений включений с каузальными операторами

Изучение систем, описываемых дифференциальными и функциональными уравнениями с каузальными операторами, введенными Л. Тонелли [1] и А.Н. Тихоновым [2], привлекает внимание многих исследователей. Отметим, что в свое время для исследования влияния излучения на температурный режим земной коры А.Н. Тихоновым были изучены задачи для уравнения теплопроводности при нелинейных краевых условиях. Им была предложена редукция, сводящая эти задачи к нелинейным интегральным уравнениям типа Вольтерра. В качестве приложений полученных результатов к задачам математической физики был рассмотрен ряд задач теплопроводности, в частности, задача, об остывании тела, при лучеиспускании с поверхности.

Понятие каузального оператора оказалось мощным инструментом для унификации задач в теории обыкновенных дифференциальных уравнений, интегро-дифференциальных уравнений, функционально-дифференциальных уравнений с конечным или бесконечным запаздыванием, интегральных уравнений Вольтерра, функциональных уравнений нейтрального типа и др. [3]. Различные задачи для функционально-дифференциальных уравнений с каузальными операторами были рассмотрены в работах [4-10]. В частности, граничная и периодическая проблемы изучались в [5,7]. В настоящей работе применяется метод негладких интегральных направляющих функций в исследовании периодической задачи для дифференциального включения с многозначным каузальным оператором.

Основные идеи метода направляющих функций были сформулированы М.А. Красносельским и А.И. Перовым еще в середине прошлого века [И, 12]. Будучи геометрически наглядным, этот метод первоначально применялся к изучению периодических и ограниченных решений обыкновенных дифференциальных уравнений (см., например, [13-15]. Позже этот метод был распространен на случай дифференциальных включений (см., например, [16, 17]), функциональнодифференциальных уравнений и включений (см., например, [18, 19]) и другие объекты. Как известно, дифференциальные включения - достаточно удобный математический аппарат, описывающий нелинейные управляемые системы с обратной связью, системы автоматического регулирования, системы с разрывными и импульсными характеристиками и другие объекты современной инженерии, механики, физики (см., например, [16,17]). Сфера применения метода направляющих функций была расширена на изучение качественного поведения и бифуркации решений (см., например, [20]), асимптотики решений (см., например, [21,22]). Эти и другие аспекты метода направляющих функций и его приложений, а также дополнительную библиографию, можно найти в недавно вышедшей монографии [23].

Работа организована следующим образом. После предварительных сведений (и. 1), где определяется, в том числе, понятие многозначного каузального оператора, формулируется периодическая задача для дифференциального включения с каузальным мультиоператором, приводится основной результат работы как для включений с выпуклозначным и замкнутым каузальным мультиоператором (п. 2.1), так и для случая, когда правая часть включения является полунепрерывным снизу каузальным мультиоператором с невыпуклыми значениями (и 2.2).

1.    Предварительные сведения

В дальнейшем используются известные понятия и терминология из анализа и теории многозначных отображений (мультиотображений) [16,17,24,25].

Пусть ( X, dX ) ii ( Y,dY ) — метрические простраиства. Символами P ( Y ) , C ( Y ) , K ( Y ) обозначаются совокупности всех, соответственно, непустых, замкнутых или компактных подмножеств пространства Y. Если Y — нормированное пространство, то символами Cv ( Y ) и Kv ( Y ) обозначаются совокупности всех непустых выпуклых замкнутых и, соответственно, компактных подмножеств пространства Y.

Определение 1. Мулътиотобраэюение F : X ^ P ( Y ) называется полунепрерывным сверху (пн. св.) в точке x о G X, если для любого е >  0 пандется 5 >  0 такое, что из того, что d_X ( x ₀ , x ) < 5 следует, что F ( x ) С U_e ( F ( x о))- где символ U_e обозначает е- окрестность множества.

Определение 2. Мулътиотобраэюение F : X ^ P ( Y ) называется пн. св., если оно пн. св. в каждой точке x G X.

Определение 3. Мулътиотображение F : X ^ P ( Y ) называется полунепрерывным снизу (пн. сн.) в точке x ₀ G X, если для любого е >  0 найдется 5 >  0 такое, что из того, что d_X ( x ₀ , x ) < 5 следует, что F ( x о) С U_e ( F ( x )) .

Определение 4. Мулътиотображение F : X ^ P ( Y ) называется пн. сн., если оно пн. сн. в каждой тон,нс. x Е X.

Определение 5. Если мулътиотображение F полунепрерывно и сверху и снизу, то оно называется непрерывным.

Определение 6. Пусть F : X ^ P ( Y ) - некоторое мулътиотображение. Множество Г F в декартовом произведении X х Y,

ГF = {(x,y) | (x,y) Е X х Y, у Е F(x)} называется графиком мулътиотображения F.

Определение 7. Мулътиотображение F : X ^ P ( Y ) называется замкнутым, если его график Г F есть замкнутое множ метео в пространстве X х Y.

Мультиотображение будем называть мультифункцией, если оно определено на подмножестве числовой прямой.

Определение 8. Мулътиотображение F : X ^ P ( Y ) называется компактным, если образ F ( X ) .является относительно компактным в Y.

Определение 9. Однозначное отображение f : X ^ Y называется сечением мулътиотображения F, если f ( x ) Е F ( x) для каждого x Е X.

Пусть E - сепарабельное банахово пространство: L ¹ ([ a,b ]; E ) обозначает банахово пространство (классов эквивалентности) суммируемых по Бохнеру функций f : ^[ a, b ^] ^ E.

Определение 10. Непустое множество М С L 1([a,b]; E) называется разложимым. сели для любых f,g Е Ми любого измеримого по Лебегу множества m С [a,b] выполнено f Km + gK([a,b]\m) Е М, где кт - характеристическая функция множества m.

В дальнейшем будет использоваться следующая теорема Брессана - Коломбо -Фрышковского о непрерывном сечении (см., например, [24]).

Лемма 1. Пусть X - сепарабельное метрическое пространство. Тогда любое пн. сн. мулътиотображение F : X ( L 1 ([ a,b ]; E ) с замкнутыми разложимыми значениями имеет непрерывное сечение.

Пусть I - замкнутое подмножество R , снабженное мерой Лебега.

Определение 11. Мулътифункуия F : I ^ K ( Y ) называется измеримой, если для любого открытого подмножества W С Y его прообраз

F— ¹ ( W ) = {t е I : F ( t ) С W}

• - измеримое подмножество I.

Замечание 1. Всякая пн. сн. мультифункция измерима.

Замечание 2. Всякая измеримая мультифункция F : I ^ K ( Y ) обладает измеримым сечением, то есть существует такая измеримая функция f : I ^ Y, что f ( t ) Е F ( t ) почти для всех (п.в.) t Е I.

Определение 12. Мулътиотобраэюение F : I х X ^ K ( Y ) удовлетворяет условию подлинейного роста, если существует неотрицательная суммируемая по Лебегу на I функищя а ( • ) такая, что п.в. t Е I

\^{F (} t,x ) | | := max \\у\\ < ^{а (} t ⁾⁽1 + || x\ ) . yEF ( t,x )

В дальнейшем мы будем использовать определения и элементарные свойства топологической степени однозначных и многозначных векторных полей (см., например, [11,17,24,25]).

Пусть T >  0 1i а >  0 - данные числа. Символами C ([ kT — а, ( k + 1) T ]; R n ) п L ¹(( kT, ( k + 1) T ); R n ), г де k Е Z, обозначаем соответствующие пространства непрерывных и суммируемых функций с обычными нормами. Для подмножества N С L ¹ (( kT, ( k + 1) T ); R n ) i т т Е ( kT, ( k + 1) T ) сужeiine N ii a, ( kT,T ) определяется как N I ( kT,T )= ^{f | ( kT,T )^{: f Е N}}-

Определение 13. Будем говорить, что Q - каузальный мультиоператор, если для каждого k Е Z мульти-отобрао/сснис

Q : C ([ kT — а, ( k + 1) T ]; R n ) ( L ¹ (( kT, ( k + 1) T ); R n )

задано таким образом, что для каждого т Е ( kT, ( k + 1) T ) и для любых

и ( • ) ,v ( • ) Е C ([ kT — а, ( k + 1) T ];R n )

условие и | [ кт-а,т ]= v | [ kT-а,т ] еле чет Q ( и ) | ( кт,т )= Q ( v ) | ( кт,т ) .

Рассмотрим примеры каузальных мультиоператоров. Обозначим C банахово пространство C ([ —а, 0]; R n ) .

Пример 1. Пусть мультиотображение F : R хСд Kv (R n ) удовлетворяет следующим условиям:

( F 1) мульти функция F ( -,c ) : R ^ Kv (R n ) допускает измеримое сечение для каждого c Е C ;

( F 2) мультиотс)бражеппе F ( t, • ) : C ^ Kv (R n ) полунепрерывш) сверху для п.в. t Е R;

( F 3) для любого r >  0 найдется локально суммируемая неотрицательная функция П_г ( • ) Е Ь1_ОС (R) такая, что

|F (t,c) || := sup {|y| : у Е F (t, c)} < Пг (t) п .в. t Е R , для всех c Е C, |c| < r.

Известно (см., например, [24,25]), что при условиях ( F 1) — ( F 3) для каждого k Е Z, определен мультиоператор суперпозиции

P f : C ([ kT — а, ( k + 1) T ]; R n ) ( L ¹ (( kT, ( k + 1) T ); R n ) ,

P f ( и ) = { / g L ¹ (( kT, ( к + 1) т ]; R n ) : / ( t ) g F ( t,^ )п.в. t G ( kT, ( k + 1) T )} .

Здесь u_t GC опредедeno как u_t ( 6 ) = и ( t + 6 ) , 6 G [ —a, 0] . Мультпсшератор PF является каузальным.

Пример 2. Пусть F : R х С ^ Kv (R n ) - мультиотображение, удовлетворяющее условиям ( F 1) — ( F 3) примера 1. Пусть {K ( t, s ) : —то < s < t <  + то} - непрерывное семейство линейных операторов в R n и m G L1_oc (R; R n ) - данная локально суммируемая функция. Для каждого к G Z рассмотрим интегральный мультиоператор типа Водьтерра G : C ([ kT — а, ( к + 1) T ]; R n ) ( L ¹ (( kT, ( к + 1) T ); R n ) , определенный как

t т.е.

G ( и )( t ) =

m ( t ) +

kT

K ( t, s ) F ( s, us ) ds,

t

G ( и ) = y_y G L ¹ (( kT, ( k + 1) T ); R n ) : y ( t ) =

m ( t ) + j K ( t, s ) / ( s ) ds : / G P f ( и )} .

Мультиоператор G также является каузальным.

kT

Пример 3. Пусть мультиотображение F : R хС ^ K (R n ) удовлетворяет следующему условию почти полунепрерывности снизу:

(FL ) найдется последовательность nenejосекающихся замкнутых множеств {Jn}, Jn С R n = 1 , 2 ,... такая. что: ( i ) meas (R \ [J n J_n ) = 0; ( ii ) сужeiine F на каждое множество Jn х С полунепрерывно снизу.

При условиях ( FL ) , ( F 3) (см., например, [24,25]) для каждого k G Z мультиоператор суперпозиции

P f : C ([ kT — а, ( k + 1) T ]; R n ) ( L ¹ (( kT, ( k + 1) T ); R n )

также определен и каузален.

2.    Математическая модель

Принимая за основу схему, предложенную в [3], рассмотрим следующую модель управляемого ядерного реактора. Будем считать, что его динамика описывается следующей системой функционально-операторных уравнений:

x (t) = £ вк л -1 [ x (t) — yk (t)] — P л -1 [1 + x (t)] v (t),(1)

к =1

Ук(t ) = xk[ x(t) — Ук(t)],   k = 1,2 ,...,m,(2)

v G U(x).(3)

Здесь x обозначает мощность реактора: y_k - потоки медле:шых нейтронов: в_к, P, Л и A_k, k = 1 , 2 ,..., m - некоторые константы; v - функция управления, удовлетворяющая условию обратной связи (3) с каузальным мультиоператором U.

Конкретный вид мультиоператора U зависит от условий задачи. В частности, он может быть выбран в следующей форме (см. [3]):

U ( x ) =

∞ v : v (t) = а о x (t) + ^^ aj x (t — tj j=1

t

)+/

-∞

Y ( t - s ) f ( s ) ds, f G P f ( x )

где tj - положительные константы, 52 j =1 |aj| <  to , | y | G L 1(0 , to ) , PF - мультиоператор суперпозиции, порожденный мультиотображением F ( t, с ) , удовлетворяющим условиям ( F 1) — ( F 3) пли ( FL ) , ( F 3) .

Заметим, что подстановка включения (3) в уравнение (1) ведет к тому, что относительно переменной z(t) = (x(t),y 1(t), ...,ym(t)) задача приводится к каузальному включению типа

z ( t ) G Q ( z )( t ) .

Отметим, что существование периодических решений включения (4), а также исследование устойчивости его решений представляет значительный интерес с физикотехнической точки зрения.

3.    Периодическая задача для включений с каузальными мультиоператорами

Обозначим CT пространство непрерывных Т-периодических функций x : R ^ Rn с нормой ||x||c = sup ||x(t)||. Через ||x^2 обозначим норм)" в пространстве LL2

\\x\\ 2 =

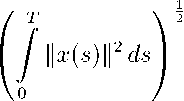
Для определения понятия периодического каузального мультиоператора рассмотрим для k G Z следующий оператор сдвига, jk : L ¹ (( кТ, ( к + 1) Т ); R ⁿ ) ^ L ¹ ((0 ,Т ); R n ): jk ( f )( t ) = f ( t + кТ ) .

Определение 14. Каузальний мулътиоператор Q низ ивается Т-периодическим, если для каждых x G CT г1 k G Z выпо.Mieno jk ( Q ( x | [ _kT-T, ( k +i) T ])) = Q ( x | [ _-T,T ]) •

Для обеспечения периодичности каузальных мультиоператоров в вышеуказанных примерах достаточно полагать, что мультиотображения F являются Т -периодичными по первому аргументу: F ( t + Т, с ) = F ( t, с ) для всех ( t, с ) G R х C и в примере 2 дополнительно считать, что функция m ( t ) и семейство K ( t, s ) так же Т -периодичны:

m ( t + Т ) = m ( t ) для всех t G R;

K ( t + Т, s + Т ) = K ( t, s ) для всех —to < s < t <  + to .

Ясно, что условие Т -периодичности каузального мультиоператора позволяет рассматривать его только на пространстве C ([ —т,Т ]; R n ) .

Сформулируем теперь основную задачу:

Для заданного Т -периодического каузального мультиоператора Q найти решение следующего операторного включения:

x G Q ( x ) ,                                       (5)

где x G CT - абсолютно непрерывная функция.

• 3.1.    Случай выпуклозначного каузального мультиоператора

Обозначим LT пространство суммируемых Т -периодических функций f : R ^ R n. В этом разделе предполагаем, что Т -периодический каузальный мультиоператор Q : CT ^ Cv ( LT ) имеет выпуклые значения и удовлетворяет следующим условиям: ( Q 1) для любого ограничениеэго линейного оператора A : LT ^ E, где E - банахово пространство, композиция A ◦ Q : CT ^ Cv ( E ) - замкнутый мультиоператор;

( Q 2) существует не отрицательная Т -перподнческая суммируемая функция а ( t ) такая, что

||Q(X)(t)|| < а(t)(1 + ||x(t)||) п.в. t G R, для каждой функции x G CT•

Для обеспечения условия ( Q 1) в примерах 1 и 2 достаточно предполагать, что помимо вышеуказанных условий периодичности, мультиотображение F удовлетворяет условиям ( F 1) - ( F 3) (см. [16]. теорема 1.5.30). а для выполнения условия ( Q 2) можно предположить в примере 1 выполненным условие подлинейного роста, а в примере 2 следующее условие глобальной интегральной ограниченности

I F ( t,c ) |< Y ( t ) п.вЛ G [0 ,Т ]

для некоторой неотрицательной суммируемой функции y ( t ) •

Для изучения периодической задачи (5) используется теорема о точке совпадения для линейного фредгольмова оператора и многозначного отображения. Введем необходимые обозначения.

Пусть E 1, E 2 - банаховы пространства; U С E 1 - ограниченное открытое множество; l : Dom l С E 1 ^ E ₂ - линейный фредгольмов оператор нулевого индекса такой, что Im l С E ₂ замкнуто.

Рассмотрим непрерывные линейные операторы проектирования p : E 1 ^ E 1 и q : E ₂ ^ E ₂ такие. что Im p = Ker l, Im l = Ker q. Символом l_p обо значим сужение оператора, l ii a, Dom l C Ker p.

Далее, пусть непрерывный оператор k_p,_q : E ₂ ^ Dom l C Ker p определен соотношением k_p,_q ( y ) = l- 1( y — q ( y )) , y G E ₂; канонический оператор проектирования п : E ₂ ^ E ₂ / Im l имеет вид п ( y ) = y + Im l, y G E ₂; i1 ф : Coker l ^ Ker l - непрерывный линейный изоморфизм.

Пусть G : U ^ Kv ( E ₂) замкнутое мультиотображение такое, что

• ( a )    G ( U ) - ограниченное подмножество E ₂;

• ( b )    мультиотображение k_p,_q ◦ G : U ^ Kv ( E 1) компактно и полунепрерывно сверху.

Справедливо следующее утверждение [24, лемма, 13.1].

Лемма 2. Пусть

• (г)    l ( x ) G ^G ( x ) д^я всеж A G (0 , 1], x G Dom l С dU;

• (ii)    0 G nG ( x ) для всех x G Ker l С dU;

• (Ш) degKer i ^{( фпG}|^ Ker l,, U Ker l ) = 0, где символ deg_Ker l обозначает топологическую степень многозначного векторного поля, вычисляемую в пространстве Ker l, _и U Ker i = U C Ker l.

Тогда l z i G имеют точку/ совпадения в U. т.ю найдется x Е U такое, что l ( x ) Е G ( x ).

Напомним теперь некоторые понятия негладкого анализа (см., например, [27]).

Пусть в R n 'задана, локально л:шшпцева функция V : R n ^ R . Для x Е R n 1i v Е R n обобщенная производная Кларка V 0( x ; v ) функции V ( ■ ) в точке x по направлению v задается выражением

V0(x; v) =    lim    V(z + t") " V(z), z→x         t t ^ 0+ где z Е Rn. Тогда, обобщенный градиент Кларка, dV(x) фушщии V (■) в тсжке x определяется следующим образом:

dV ( x ) = y_y Е R n : (y, v) < V ⁰( x ; v ) для всех v Е R n} .

Известно, что мультиотображение dV : R n ( R n имеет выпуклые компактные значения и полунепрерывно сверху (см., например, [27]). В частности, это означает, что для каждой непрерывной функции x : [0 , T ] ^ R n множество суммируемых сечений мультифункции t ( dV ( x ( t )) непусто.

Напомним, что локально липшицева функция V : R n ^ R называется регулярной, если для каждого x Е R n и v Е R n существует производная по направлению V‘ ( x, v ) и она совпадает с V ⁰( x, v ) . Известно, в частности, что выпуклые функции регулярны.

Развивая понятия, введенные в [11,17,19], дадим следующие определения.

Определение 15. Локально липшицева функция V называется невырожденным потенциалом, если найдется K >  0 такое, что 0 / dV ( x ) для всех x Е R n : ||x|| > K.

Если функция V является невырожденным потенциалом, то топологическая степень многозначного векторного поля dV одна и та же на всех шарах BK’ с центром в нуле радиуса K‘ > K. Это общее значение называется топологическим индексом V II обозначается Ind V.

Определение 16. Регулярная функция V : R ⁿ ^ R называется строгой негладкой интегральной направляющей функцией для включения (5), если найдется N >  0

такое, что

^0 ^{(и (} s ) ^{,f (} s ) )

ds >  0

для. всех f E Q ( x ) ,

для всех суммируемых сечений и ( s ) Е dV ( x ( s )) и каждой абсолютно непрерывной функции x Е CT тако/и что |x|2 > N 11 |x‘ ( t ) || < |Q ( x )( t ) || h.g. t E [0 ,T ].

Теорема 1. Пусть V : R ⁿ ^ R - строгая негладкая интегральная направляющая (функция задачи (5) с T-периодииеским каузальпым оператором Q, удовлетворяющим условиям ( Q 1) - ( Q 2) такая, что Ind V = 0. Тогда задача (5) имеет решение.

Замечание 3. Отметим, что условия теоремы выполнены, если, например, функция V четна пли удовлетворяет ус.товию коэртштивиости. т.е. lim V ( x ) = ±^. ∥ x ∥ → + ∞

Для доказательства теоремы понадобится следующее утверждение (см. [22]).

Лемма 3. Пусть V : R n ^ R - регулярна,я функция, x : [ a,b ] ^ R n - абсолютно непрерывная функция. Тогда функция V ( x ( t )) таксисе является абсолютно непрерывной, и справедливо следующее равенство:

V ( x ( t ))

-

V ( x (0)) = f

V ⁰( x ( s ) , x ( s )) ds,

t G [0 ,T ] .

Доказательство. Сведем задачу к лемме 2, обосновав разрешимость следующего операторного включения lx G Q (x),                                           (Т)

где l : Dom l := {x G CT : x абсолютно непрерывна } C CT ^ LT - линейный фредгольмов оператор нулевого индекса. Тогда Ker l = R n, проекция n : LT ^

T

R n может быть за дана формулой nf = T J f ( s ) ds, и мультиоператоры nQ и k_p,q Q 0

выпуклозначны и компактны на ограниченных подмножествах.

Пусть для некоторого A G (0 , 1] функция x G Dom l является решением включения

l ( x ) G AQ ( x ) .

Это означает, что x ( • ) является абсолютно пепрерывиой функцией такой, что x' ( t ) = Af ( t ) п.в. t G [0 , T ]. для пекоторого f G Q ( x ). Предполс>жим. что ||x||2 > N.

Тогда, с одной стороны, используя (6), имеем

<^{и (} s ) ^,Af ⁽ s ) ^

ds >  0

для каждого суммируемого сечения и ( s ) G dV ( x ( s )) . С другой стороны, применяя лемму 3, получаем

TT

/ (^{и ( s} ) ^{,Af ( s} ) ) ^ds = у J (^{и ( s} ) ^,x' ^{( s} ) ) ^ds<  00

T

< у JV0(x(s),x(s)) ds = у (V(x(T)) - V(x(0))) = 0, для каждого суммируемого сечения и (s) G dV (x(s)).

Из полученного противоречия следует, что |x|2 < N. Но тогда найдется и M >  0 такое, что |x|c < M. В качестве U возьмем шар Br C CT с центром в нуле и радиуса r = max {M, NT~ ¹ / ² } . Тогда имеем

l ( x ) G AQ ( x )

для всех x G dU, A G (0 , 1) .

Пуств теперв u G dU П Ker l произволвио. Посколвку |u| > NT^{- 1} /"2. из определения строгой негладкой интегральной направляющей функции получаем, что

0 <^{и ( s} ) ^{,f ( s} ) )^d

s> 0

для каждого суммируемого сечения и ( s ) Е dV ( и ) и f ( s ) Е Q ( и ) . Но, полагая и ( s ) = и, получаем

(^{u,f (} s ) ^ds = (и 10 f ⁽ s ) ds) = T^^u,nf) >  0

• ii.    следовательно. (и, у) >  0 для всех и Е dV ( и ) , у Е nQ ( и ) .

• 3.2 . Случай полунепрерывного снизу каузального мультиоператора

Это означает, что 0 / nQ(и) и мультиноля dV(и) и nQ(и) не допускают противоположных направлений для и Е dU П Ker l и, следовательно, они гомотопны на dU П Ker l. По свойству гомотопической инвариантности тогда имеем deg(nQ|UKer l ,UKer i) = deg(dV, UKer i) =0, где UKer l = U П Ker l. Таким образом, все условия леммы 2 выполнены и задача (7), а, следовательно, и задача (5) имеют решение.                                  □

Теперь рассмотрим периодическую задачу для класса включений с невыпуклозначными полунепрерывными снизу каузальными мультиоператорами. Именно, будем предполагать, что T -периодический каузальный мультиоператор Q : CT ^ P ( LT ) удовлетворяет условию

(QL) Q полунепрерывен снизу и имеет замкнутые разложимые значения ii условию (Q2).

В качестве примера каузального мультиоператора, удовлетворяющего условиям ( QL ) ii ( Q 2) можно рассмотреть суперпсхзшщонный мультпоператор PF, порожденный T -перподпческпм по первому аргументу мулвтиотображеиием F : R xC ^ K (R n ) , удовлетворяющим условию почти полунепрерывности снизу ( FL ) и условию подлинейного роста.

Теорема 2. Пусть Q : CT ^ P ( LT ) - T-периодический каузальный оператор, удовлетворяющий условиям ( QL ) и ( Q 2) и V : R n ^ R - строгая негладкая интегральная направляющая функция для соответствующей задачи (5) такая, что

Ind V = 0 .

Тогда задача (5) имеет решение.

Доказательство. Применяя лемму 2, найдем непрерывное сечение q : CT ^ LT мультиоператора Q. Для отображения q имеем соотношение

T

(^{и (} s ) ,q ⁽ x ⁾⁽ s ) )

ds >  0

для всех суммируемых сечений и ( s ) Е dV ( х ( s )) и для каждой абсолютно непрерывной функции x Е CT тако!1. что ^х^2 > N 11 Цх⁷ ( t ) || < ||Q ( x )( t ) | | п.в. t Е [0 ,T ].

Теперь, применяя « однозначную » версию леммы 2 (т.е. заменяя мультиотображение G непрерывным отображением д ) и применяя аналогичные приведенным выше рассуждения, получим решение х следующего уравнения

l ( x ) = q ( x ) , которое является решением задачи (5).

4. Пример

Рассмотрим периодическую задачу для управляемой системы, описываемой полулинейным функционально-дифференциальным включением следующего вида:

X ( t ) G Ax ( t ) + F ( t, x_t )                                  (8)

x (0) = x ( T ) .                                        (9)

Здесь A : R n ^ R n - линейный оператор, а, мультиотображеиие F : R x C ^ Kv (R n ) удовлетворяет условию T -периодичности по первому аргументу и условиям ( F 1) - (F 3) примера 1 пункта 1. Тогда определен мультиоператор суперпозиции

Pf : C ([kT - а, (к + 1)T]; Rn) ( L1 ((kT, (к + 1)T); Rn), удовлетворяющий условию (Q1) (см. [16, теорема 1.5.10]). Для выполнения условия (Q2) предполагается справедливость условия подлинейного роста для мультиотображения F.

Пусть функция V : Rn ^ R имеет еле да-тощий вид: V(x) = ^ + V(x), где V : Rn ^ R - регулярная функция такая, что V удовлетворяет условию коэрцитивности. Ясно, что V является регулярной функцией и dV (x) = x + dV (x)

(см. [27, следствие 3 из теоремы 2.3.3]).

Предположим, что для некоторого N >  0 и каждой абсолютно непрерывной функции x G CT такой. что ||x ||₂ > N 11 ||x' ( t ) || < ^PF ( x )|| , для всех y G PF ( x ) , и G dV ( x ) , t G [0 , T ] выполнены условия:

Hl) (Ax, v) > (u, x) ;

H2) (U,X)>(U,x).

Применение теоремы 1 позволяет получить следующий результат.

Теорема 3. Пусть квадратичная форма (Ax,x) удовлетворяет для некоторого е >  0 условию

(Ax, x^ > Е|x| ²

для всех: x G R n. Если

|PF ( x ) В ₂   1              B9V ( x ) В 2 _< у

,,

||жП - ^ + Го |x| 2        3       Н^П - ^ + Го    |x| 2        3

для всех абсолютно непрерывных x G CT, где

^BPF ^{( x} ) ¹ 2 = SUp ^ВУ^В 2 , ^{|dV ( x} ) ¹ 2 = SUp ||^{U 1} 2 , ycPF ( x )                          e _£dv ( x )

то задача (8), (9) имеет решение.

Доказательство. Покажем, что функция V является строгой негладкой интегральной направляющей функцией для включения (8). Отметим, что каждое u G dV(x) имеет вид и = x + u, где u G dV (x).

Действительно, для произвольных y G PF ( x ) , u G dV ( x ) согласно ( H 1) , ( H 2) имеем

TT j {u(s), Ax(s)+ y(s)) ds = j {x(s)+ u(s), Ax(s) + y(s)) ds = 00

T

T

T

T

= j {Ax ( s ) , x ( s ) ) ds + j {Ax ( s ) , e( s ) ) ds + j {x ( s ) ,y ( s ) ) ds + j {u(s ) ,y ( s ) ) ds >

T

T

T

T

> J* {Ax ( s ) , x ( s ) ) ds + У {u ( s ) , x ( s ) ) ds + j {x ( s ) ,y ( s ) ) ds + У {u ( s ) , x ( s ) ) ds > z^«z                                                                                                  z^«z

> s^x^ 2 - yxy 2 ^dV ( x ) У 2 - yxy 2 yPp ( x ) У 2 - yxy 2 ^dV ( x ) У 2 >  0

для достаточно больших значений yxy2.

□

Автор искренне благодарен профессору В.В. Обуховскому за полезные обсуждения затронутых в статье вопросов.

Работа проводилась при финансовой поддержке РФФИ (гранты 1 б₍ 01 00б₍ 68, 1601-00386), РФФИ-Тайванъ (грант 14 01 92004) к Российского научного фонда (грант 14-21-00066, выполняемый в Воронежском госуниверситете).