Введение операторной формы позволяет представить прямое ПФ (первое соотношение)³ ) как S = F 5 . При этом F ² 5 ( t ) = 5 ( — t ) и F ⁴ 5 ( t ) = 5 ( t ), где F ⁿ означает повторное n -кратное применение ПФ.

Если к уравнению d2 5(t)  „2^2П + 1

+ 4 п ²1-- 1 ² 1 5 ( t ) = 0,      (1)

dt         | 2n     J где в качестве функции 5(t) временно не имеется в виду какой-либо определенный сигнал, применить ПФ (с использованием правил для ПФ от dd5(t) и от t2 • 5(t)), то уравнение (1) преобразуется в свою "частотную" форму (2):

^d S ⁽ v ) + 4 п ^{2 f} 2 ^ + 1 — v ² ) S ( v ) = 0,     (2)

dv2        ( 2n      J где S (v) = F [5(t)] .

Уравнение (2) по форме идентично (1). Но поскольку решением уравнений такого вида являются функции Эрмита—Гаусса⁴ ) H . ( л/2 П t ) exp ( —n t ² ) , то именно эти функции являются (исходя из (2)) собственными функциями операции (оператора) преобразования Фурье.

Нормированные функции Эрмита—Гаусса { Т _n ( t )} _n = ₁₂ служат набором, образующим базис, и имеют вид

^2

P.(t) =       Hn (V2^ t)exp(—nt).(3)

V2nn!     V

Эти функции являются собственными функциями оператора ПФ F , т. е. удовлетворяют уравнению

F (Pn (t) ) = A. P n (t),(4)

где An = j n — собственные значения, соответ- ствующие n-й собственной функции.

Поскольку собственные функции Эрмита—Гаусса { Г _n ( t ) }        составляют базис, то любой

L           J n=1,2,...,то сигнал (как функция) может быть представлен рядом по этим собственным функциям:

то

5 ( t ) = ^ A n Т n ( t ),                 (5)

n =0

где коэффициенты A_n = j P _n ( t ) 5 ( t ) d t .

Применение к (5) оператора F позволяет получить в аналогичной форме представление ПФ сигнала 5 ( t ):

TO

F ( 5 ( t ) ) = ^ A n j ^— n P n ( t ).           (6)

n =0

Оператор вращаемого преобразования Фурье порядка а (т. е. F ^а ) может быть определен на основе действия оператора традиционного ПФ на свои собственные функции:

F ^a ( Г n ( t ) ) = ( A n ) “ P n ( t ) = ( j ) ^— “n P n ( t ) . (7)

Таким образом, оператор ВПФ имеет те же собственные функции, что и оператор ПФ, а собственные значения ВПФ с угловым параметром а равны значению ( A n ) “ .

Оператор ВПФ является линейным, поэтому ВПФ любого сигнала может быть выражено рядом, который по структуре аналогичен ряду (6):

TO

{ F ^a ( 5 ( t ) ) } ( t ) = Х A n j ^{— a n} P n ( t ).      (8)

n =0

Результат применения к сигналу оператора ВПФ может быть представлен также в виде (чаще используемом) интегрального преобразования с ядром B _a ( t , t ) [1, 2, 8]. Это осуществляется подстановкой в (8) выражения для коэффициентов A_n из (5):

{ F “ ( 5 ( t ) ) } ( t ) = j B „ ( t , t ') 5 ( t ') d t ',         (9)

TO

Ba (t, t ') = X(An )“ P n (t) Т n (t j = n=0

= V2"exp |^—n (t2 +1 '2 )Jx to •—an x£ jn^H. (V2n t) h, (V2nf).     (10)

n =0 ² n !

Из выражения (10) ядра ВПФ может быть получена более простая форма (11). Это реализуется путем использования у ВПФ вместо а приведен- ной (или "нормированной") величины5) ф: ф = а / (п /2). При вращении время-частотной плоскости на угол а в пределах 0 < а < п, "нормированный" параметр ф меняется в пределах 0< ф <2:

e ( — j ( па,/ 4- а / 2 ) )

х exp ( j п ( t ² ctg а - 2 tt 'cosec а + t '² ctg а ) ) , (11)

где а = ф • п /2 и а = sign(sin а ).

Следует заметить, что выражения (7)-(10) не зависят от нормировки параметра а и остаются справедливыми при любой интерпретации параметра ВПФ — и как фактического углового параметра а , и как нормированного параметра ф .

Ядро (11), определенное отдельно для ф = 0 и ф = 2, получает упрощенное значение; оно выражается дельта-функциями:⁶⁾ B ₀ ( t , t ') = S ( t - t '); B ₂( t , t ') = 5 ( t + t ').

Из основных свойств оператора ВПФ, приведенных в достаточно полной форме в [3, 5, 7, 13], полезно отметить наиболее важные и используемые в последующем анализе:

• ■    линейность оператора ВПФ ( F );

• ■    соответствие оператора F ^{( ф} = 1) (т. е. F ^{( а} = ^п/2) ) традиционному оператору ПФ ( F );

• ■    аддитивность оператора ВПФ по угловому параметру F ^а ' Г ^а 2 = р ^{а 1 + а 2} .

С точки зрения реализации ВПФ небезынтересна возможность его применения к двумерному сигналу $ ( t 1 , t ₂) (например, к изображению) и выполнение этого преобразования оптическими методами [3, 5]. ВПФ описывает распространение луча (эмулирующего сигнал) в оптической среде с квадратично изменяющимся коэффициентом преломления, и если свет с распределением интенсивности $ ( t 1 , t ₂) падает на одну сторону такой оптической среды с толщиной aL , то на другой стороне этого слоя получается двумерное ВПФ с параметром а . Так что "кусок" такой оптической среды может использоваться для аналогового вычисления ВПФ.

Далее у координатных переменных в области ВПФ будут использоваться индексы типа t_a . Так что t ₀ = t и t_{n /2} = v ; $_а — ВПФ сигнала, $ ₀ = $ , $_{п /2} = S (где S — ПФ сигнала $ ). Кроме того, вре-мя-частотное преобразование (ВЧП) Вигнера— Вилле в зависимости от контекста будет обозначаться как W [ $ ] , W [ $ ] ( t , v ) или как S w ( t , v ).

ВПФ И ВРЕМЯ-ЧАСТОТНОЕ

ПРЕОБРАЗОВАНИЕ ВИГНЕРА—ВИЛЛЕ

Взаимосвязь ВПФ сигнала и его ВЧП Вигнера—Вилле является отражением одного из наиболее значительных свойств ВПФ.⁷⁾ Свойство состоит в том, что применение операции ВПФ с параметром а к сигналу $ ( t ) соответствует вращению распределения (результата преобразования) Вигнера—Вилле на угол а по часовой стрелке. Распределение на время-частотной плоскости, получаемое в результате ВЧП Вигнера—Вилле, определяется соотношением:

W [ $ ( t ) ] = S w ( t , v ) =

• =    | $ ( t + 1 '/2) • $ * ( t - t '/2) • exp ( - 2 п jvt ' ) d t ', (12)

где W — оператор ВЧП Вигнера—Вилле; S W ( t , v ) — время-частотное распределение, результат ВЧП сигнала $ ( t ) [14-17]; — символ комплексного сопряжения.

Базовые свойства преобразования Вигнера— Вилле свидетельствуют, что его маргиналы (интегралы по одной из переменных результата ВЧП) дают распределение энергии сигнала (квадрата его модуля) в частотной и во временной областях, а полное интегрирование дает соответственно полную энергию сигнала:

I $ ( t )| ² = 1 S W ⁽ t , ^{v )d v} ,

I S w ( ^v )|² = J S w ⁽ t , ^{v )d} t ;

полная энергия сигнала равна J S W ( t , v )d t ; S W ( t , v ) интерпретируется как двумерное распределение энергии сигнала во время-частотной области. ⁸⁾

Более сложные свойства получаются из рассмотрения вращения время-частотного распределения

Вигнера—Вилле (результата этого ВЧП) и применения к нему преобразования Радона. Так, если ввести оператор R _а вращения двумерного распределения на угол а против часовой стрелки, то применение этого оператора к соотношению (12) и сравнение полученного результата с распределением Вигнера—Вилле для ВПФ с параметром а /( п /2) приводит к соотношению (13) или к эквивалентному ему соотношению (14):

R -„ W [ 5 ₀] = W [ s . /( . /2) ],               (13)

W [ ] = R - a ( n /2) W [ s 0 ].               (14)

Поскольку и оператор ВПФ, и оператор вращения R a имеют свойство аддитивности относительно своих угловых параметров (т. е. R _a 1 R _a 2 = R _a 1 _+a 2 и f ^a i f ^{a 2} = f ^{1 2} ), то аналогичное свойство переносится на взаимосвязь оператора Вигнера—Вилле с оператором вращения результата применения ВЧП к сигналу [7]. Расширенное свойство аддитивности по угловым параметрам операторов R _а и W [ s _a ] определяется соотношением

W [ S a 2 ] = R (- a 2 ( п /2)+ a 1 ( п /2) W [ S a 1 ].         (15)

Еще одно свойство, связанное одновременно с ВПФ, ВЧП Вигнера—Вилле и с преобразованием Радона, установлено Лохманом [5, 8]. Преобразование Радона⁹ ) RAD _у некоторой функции двух переменных (такой, как распределение Вигнера— Вилле) зависит от углового параметра (назовем его у ), и результатом преобразования является проекция этой функции на ось, составляющей угол у с осью t (в координатной системе ( t , v )). При этом термин "проекция" понимается (в смысле функционального анализа) как интеграл преобразуемой функции вдоль соответствующей оси. Используя введенные обозначения, анализируемое свойство выражается соотношением (16) или эквивалентным ему соотношением (17):

RAD _y { W [ s ] } = | F ^{[ a}'^{7 /( n /2)]} [ s ] |² ,          (16)

I F ^a [ s ] |² = RAD . /2) { W [ s ] } .           (17)

Оператор преобразования Радона в соответствии с трактовкой его процедуры может быть связан с оператором вращения R соотношением (18)

RAD =a ) { W [ s ] ( t , v ) } = J R - a { W [ s ] ( t , v ) } d v , (18) где операторы RAD и R действуют на распределение Вигнера—Вилле (сигнала) в точке ( t , v ).

Соотношения (17) и (18) отражают обобщенные свойства распределения Вигнера—Вилле, которые получены при его анализе совместно с оператором ВПФ, и операторами вращения, и Радона. Еще одно обобщение получается, если дополнительно ввести так называемый оператор среза S _а . Действие этого оператора на время-частотное распределение (или любую другую функцию) таково, что результатом являются значения ВЧР на оси, составляющей угол а с осью времени в плоскости время—частота, т. е. в координатной системе ( t , v ). Кроме того, результат применения S _а является одномерной функцией, т. к. две переменные ВЧР теперь принадлежат одной прямой. (Заметим, что после интегрирования оператор среза дает оператор Радона, и в этом их сходство и различие).

Понятие оператора среза позволяет представить еще одно обобщенное свойство ВЧП Вигнера—Вилле, которое объединяет это ВЧП с операторами среза, Радона, ПФ и двумерным ПФ ( F ₂). Это свойство выражается соотношением (16)¹⁰⁾

F • RAD . = a ) • W [ s ] = S a • F 2 • W [ s ] .       (16)

ДИСКРЕТНОЕ ВПФ

Дискретные сигнал ({ s i } i = ₀ , ₁ ,_, _N- 1 ) и его N-точечное ПФ ({ S k } _k = ₀ , ₁₌ _, _N- 1 ) связаны соотношениями [19]:

N-1

Sk =X siwk; si =^ SkW-ki,(20)

i=0

где w ^ki = (1/ V N ) exp( - 2 n jki IN ) .

В операторной форме (в нашем дискретном случае оператор — это матрица) соотношения (20) представляются в виде (21):

S = F • s ;      s = F ^{- 1} • S ,            (21)

где S = [S0,S1,...,SnJ' и s = [s0,s^...,snJt — векторы; оператор-матрица F имеет в качестве своих элементов {Fk = w(i-1)(k-1)}ik=0 1 N 1, а оператор F представляет ВПФ F(φ = 1) = F(α = π/2).

При этом F ^{( a} =2’ ) = F ^{( 9} = ²⁾ I , I — единичная матрица и выполняется соотношение (22), выражающее ортонормальность между строками (и между столбцами) матрицы F и ее комплексно сопряженной F * :

N -1

X w ^k w -l = 5_Н ( k , l = 1,2,..., N - 1 ).     (22)

i =0

Уравнение, определяющее собственные значения и собственные функции оператора ВПФ (проанализированное выше для традиционного ПФ), имеет вид Fs = A s , и поскольку F ⁹ = 2 = I , то 2 ⁴ =1 и, следовательно, A n = exp( - jn n /2) = j ^{- n} при любых целых значениях n .

Для получения собственных значений и собственных функций матрицы (оператора) дискретного ВПФ (Д_ВПФ) для нецелых значений углового параметра φ удобно воспользоваться представлением Дикинсона (Dickinson [13]) для F ⁹ в виде суммы F ^{( 9} = ^k ) , т. е. суммы матриц Д_ВПФ с целыми значениями нормированного (или приведенного) углового параметра φ = α /( π /2):

F ^{( 9} ) = X F ^kp_k ( 9 ), k =0 1⁴

P k ( 9 )   , X exp[ ji ( 9 - k ( n /2)].

4 i =1

Представление (23)¹¹⁾ позволяет показать, что собственные функции у оператора Д_ВПФ такие же, как у ПФ, а собственные значения являются φ -степенями от соответствующих собственных значений ПФ. Таким образом, если выполняется соотношение F ⁹ =1 s _n = A n s _n для целых n , то оно также выполняется и для Д_ВПФ при нецелых значениях нормированного углового параметра: F ⁹ s = X⁹s_n , или F “ ^{/(2 n} ) s„ = A^{a /(2 n} > s„ . nnn ^,        nn   n ^.

Любой дискретный сигнал (в виде вектора s ) может быть представлен разложением по ортогональным собственным векторам Д_ПФ:

N s = X Ansn , где An = sTsn — коэффициенты раз-n=1

ложения. Аналогичным образом оператор Д_ВПФ вектора s — дискретизованного сигнала представляется разложением

N

F “ s = X A n A n“ s n .               (24)

n =1

ВЗАИМОСВЯЗЬ ПРОЦЕДУР СВЕРТКИ И ПРОИЗВЕДЕНИЯ В ОБЛАСТИ ВПФ С ВЧР ВИГНЕРА—ВИЛЛЕ

До анализа особенностей применения мультиплексирования и фильтрации в области ВПФ в этом разделе будет рассмотрен ряд соотношений, которые связывают процедуру свертки и произведение двух сигналов (в обычном виде и в области α -ВПФ¹²⁾ ) с время-частотным распределением Вигнера—Вилле (ВЧР_ВВ) и с применением оператора ВПФ к результату этих операций [20, 21]. При этом будет применяться сокращенная форма записи для свертки и произведения сигналов в области ВПФ, которая ниже показана в правых частях выражений (25) и (26).

Свертку сигнала с импульсной передаточной функцией (ИПФ) фильтра или с ИПФ управляющего звена удобно анализировать на примере операторного описания свертки сигнала s и ИПФ h (ИПФ h в дальнейшем для симметрии будем условно также называть сигналом). Кроме того, для отличия от традиционной процедуры свертки s * h свертка сигналов (функций) s и h в области α-ВПФ, т. е. сигналов sα и hα , будет далее обозна чаться в виде ga = s* h. Таким образом, запись операции свертки (с явным указанием принадлежности сворачиваемых компонент (s и h) к области ВПФ) будет заменяться более компактной формой в соответствии с соотношением (25):

g a ( t a ) = F “ [ g ] = F “ [ S ] * F “ [ h ] =

a

• =    ^S a ⁽ t a ) * h a ⁽ t a ) ^ g a = ^S * ^{h .           (25)}

При α = 0 эта операция переходит в обычную свертку. При a = n /2 ( F ^{( a} = ^{п /2)} переходит в операцию ПФ — F ) она переходит в свертку ПФ от сворачиваемых компонент F [ g ] = F [ s ] * F [ h ] , которая эквивалентна равенству g = s • h ; следовательно, эта операция свертки равноценна произведению сворачиваемых сигналов. Свертка в области ВПФ с α = π /4 является чем-то промежуточным между обычной сверткой и произведением.

Точно так же (как для свертки) удобно ввести компактную форму представления произведения двух сигналов в области ВПФ. Смысл такой формы показывает выражение (26), построенное по аналогии с (25):

g a ( t a ) = F ^a [ g ] = F ^a [ S ] X F ^a [ h ] =

• =    ^S a ⁽ t a ) • h a ⁽ t a ) ^ g a = ^{S a h .           (26)}

  Как указано выше, для свертки и произведения сигналов в области ВПФ далее будет применяться сокращенная форма записи, показанная в правой части выражений (25) и (26), а форма взаимосвязи процедур свертки и произведения сигналов в области ВПФ с ВЧР_ВВ и применением оператора ПФ к результатам этих процедур будет представлена с использованием символа импликации¹³ ) ^ .

  • ■    Операция свертки двух сигналов (функций) во временной области соответствует свертке в области ВЧР Вигнера по времени:

  g ( t ) = s ( t ) * h ( t ) ^ W g ( t , v ) =

  = J W , ( t ', v ) W h ( t - t ', v )d t '.

  • ■    Произведению двух сигналов g ( t ) = = s ( t ) h ( t ) соответствует свертка ВЧР Вигнера— Вилле (ВЧР_ВВ) по частоте:

  g ( t ) = s ( t ) h ( t ) (т.е. F [ g ] = F [ s ] * F [ h ] ) ^

  ^ W g ( t , v ) = J W , ( t , v ') W h ( t ', v - v ')d v '.

  Сходное соотношение процедур имеется при осуществлении свертки а -ВПФ сигналов и произведения ВПФ сигналов:

  • ■    Свертке сигналов в области а -ВПФ соответствует свертка ВЧР_ВВ (этих сигналов) по направлению t _а:

  g a = ^s * h ^

  ^ Wg ( t «, v «) = fW ( t „, v„ ) W_h ( t„ - 1 „, v „)d t_a. g a     a*    ю               ^ a     O'    a*       ^‘a    O'      ^a    a*      ю

  • ■    Произведению сигналов в области а -ВПФ соответствует свертка ВЧР_ВВ (этих сигналов) по направлению v _a:

  a

  g a = ^s X ^h ^

  ^ ^W g _a ⁽ t a , v a ) = J ^W s _a ⁽ t a , v a ) ^W h _a ⁽ t a , v a ^- v a ) ^d v a ■

  Свойства, отражающие взаимосвязь свертки и произведения сигналов в области ВПФ, имеют более компактную форму выражения при использовании нормированного значения углового параметра а , т. е. при формулировании этих свойств в терминах параметра ф = а /( п /2). Умножение двух функций s и h в области ф -ВПФ, т. е. в области

  
  

  ВПФ с параметром а = ф ( п /2), имеет вид (27) "

  и может быть обозначено как g " = s х h :

  
  

  g " ( " ) = F " [ g ] = F " [ s ] x F " [ h ] =

  = ^s " ⁽ t " ) ^h " ⁽ t " ) ^ g " = ^s X ^h .              ⁽²⁷⁾

  
  

  Тогда выполняются следующие соотношения, связывающие применение ВПФ к свертке и произведению сигналов (в ВПФ области) с изменением величины нормированного углового параметра:

  
  

  •    F " ^{+ 1}

  
  

  "

  s х h

  
  

  "

  F " ^{+ 1} s * h

  
  

  = F " ^{+ 1} [ s ] * F " ^{+ 1} [ h ] = F " ^{+ 1}

  
  

  "

  s X ^h ;

  
  

  " +1

  
  

  = F " ^{+ 1} [ s ] x F " ^{+ 1} [ h ] = F " ^{+ 1} s * h ;

  
  

  • два взаимно дуальные соотношения, следующие из двух приведенных выше:

  
  

  "        " +1        " -1

  
  

  s x h = s * h = s * h ;

  
  

  "        " +1

  
  

  " -1

  
  

  s * h = s x h = s x h .

  
  

  Это означает, что свертка с области ф -ВПФ соответствует умножению в области ( ф +1)-ВПФ или в области (ф -1)-ВПФ. Таким же образом умножение в области ф -ВПФ соответствует свертке в области ( ф +1)-ВПФ или в области ( ф -1)-ВПФ.

  
  

  ОГРАНИЧЕНИЕ ОБЛАСТИ ОПРЕДЕЛЕНИЯ ВПФ

  
  

  В ИИС ограниченность области определения сигнала (равенство его нулю вне конечной области), называемое компактностью, реализуется почти всегда. Однако для ВПФ и ВЧР_ВВ это не так, но компактность в этом может быть получена введением дополнительного множителя в форме пря-

  
  

  моугольного импульса, или так называемого прямоугольного окна (ПО). В области а -ВПФ, ПО с переменной-аргументом t_а , шириной А t_а и нача

  
  

  лом t_{а ;0} имеет вид:

  
  

  ПО °^ ( ^А t a

  
  

  получения свойства компактности умножается на ПО:

  
  

  . Так что для

  ВПФ или ВЧР

  
  

  g a ⁽ t a ) =

  
  

  Г ( ] по

  
  

  ¹³⁾ Символ импликации ^ служит для указания того, что из левого утверждения или соотношения следует правое. (Так же символ ^ для указания того, что оба утверждения эквивалентны, т. е. из первого следует второе и, наоборот, из второго — первое). Кроме того, чтобы избежать перегрузки формул, ВЧР Вигнера— Вилле сигнала s ( t ) будет обозначаться как W _s ( t , v ), или просто как W _s .

  
  

  t a t a ;0

  АГ а

  
  

  ■ ^{Х s} a ⁽ t a ).

  
  

  В частности, придание компактности в области а = п /2 означает низкочастотную фильтрацию, поскольку вводится ПО на частотной оси.

  Получение компактности сигнала в некоторой области а -ВПФ связано с умножением его на ПО. Это соответствует свертке ВЧР_ВВ от s ( t_а ) c ВЧР_ВВ от ПО, и эта свертка должна осущест-

  
  

вляться вдоль направления t_{a + п /2}, т. е. свертка по v_a. Поэтому следует выполнить следующие преобразования.

• ■    Определяется ВЧР_ВВ для ПО:

  W ПО ( t a , V a ) = J ПО

  
  

  t „ + t '/2 - t

  
  

  Nt

  a

  
  

  x ПО

  
  

  t a - t '/2 — t A t a

  
  

  x exp( - 2 n jt ' V a )d t =

  
  

  t '

  
  

  = J ^ПО .

  
  

2A ta [1-|2(ta - ta,)/A tai x exp(-2njt ' va )dt ' =

= 2 A t a [ 1 - |2( t a - t a _; o )/ A t a ]x

X Sinc l ^{2 A} t a [ ^{1 - |2(} t a ^- t ^)/ ^A t a I ^] v a } •       ⁽²⁸⁾

• ■    W п_О ( t _a , v _a ) выражается по (28) только при ^ПО ( ( t a — t a;0 ) / ^A t a ) = ¹ и ^WTO ⁽ t a , v a ) = ^{0 —} при ПО( ( t -t ) / A t ) = 0. Замечаем, что ВЧР ВВ у \          сл ,о /       сл /                                 '                        —

является ненулевым только вдоль коридора, определяемого функцией ПО. Следовательно, ограничение области определения а -ВПФ сигнала (получение компактности средствами ПО) по t_a обеспечивает компактность ВЧР_ВВ в пределах коридора, который перпендикулярен оси t_a , т. е. компактность ВЧР_ВВ по переменной v_a .

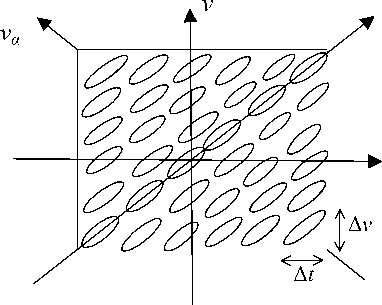
• ■    Выполнение свертки W- ПО ( t _a , v _a ) с ВЧР_ВВ W ^ ( t _a , v _a ) (сигнала в области а -ВПФ) по v_a приводит в результате к уширению W _s ( t _a , v _a ) по направлению v_a . Это уширение сравнимо по величине с шириной W- ПО ( t _a , v _a ) по v_a . Огибающая для W _ПО ( t _a , v _a ) как функция от v_a (при данном значении t_a ) равна 1/( п v_a ) и фактически не зависит от t_a . Ширина основной части этого распределения W _ПО ( t _a , v _a ) в направлении v_a равна ~1/ A t _a (рис. 1).

• ■    Из-за резких перепадов у прямоугольного окна (ПО) уширение ВЧР_ВВ по переменной v_a , т. е. в направлении, перпендикулярном к t_a , получается немного большим, чем возможная минимальная ширина ВЧР_ВВ по метрологической оценке в рамках "принципа неопределенности" [22]. Однако при использовании (для получения компактности) сглаживающего окна большей гладкости можно снизить уширение до минимальной величины, диктуемой соотношением принципа время-частотной неопределенности.

  
  
  
  

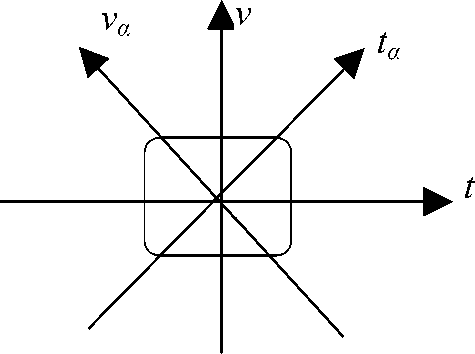
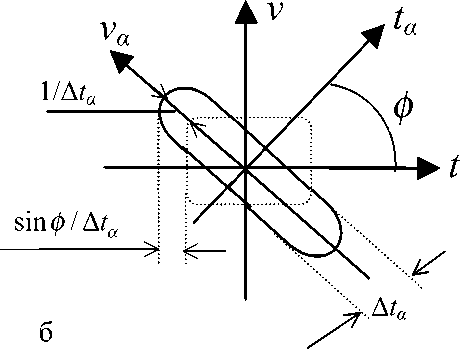
  Рис. 1. Время-частотное распределение Вигнера— Вилле (а) и характер его изменения при получении компактности по оси t_a за счет введения прямоугольного окна (б). Здесь горизонтальное направление вторичного уширения ВЧР_ВВ ( sin ф / A t _a ) находится под углом ф к v_a -направлению основного уширения 1 / A t _a , т. е. A ф в данном случае оказалось равным величине самого угла ф

  
  

Таким образом, получение компактности (ограничения области определения) ВЧР_ВВ в направлении ta (любого а-ВПФ) ведет к уширению этого распределения в ортогональном направлении (va) до величины ~1/ Ata. Это приводит также к уширению =|sin Aф|/ Ata в любом другом направлении в области ВПФ, отличающемся на угол Аф.

Отмеченные закономерности уширения ВЧР_ВВ в направлении, ортогональном к тому, по которому получают компактность ВЧР введением ПО, отражают модификацию общего принципа неопределенности. Этот принцип свойственен всем время-частотным распределениям (в том числе Вигнера и вейвлет-представлению сигнала) безотносительно к вращению ( t , v )-плоскости. Согласно этому принципу вычисленное значение ВЧР_ВВ не может быть локализовано в области, меньшей чем А t _a А v _a ~ 1 ; это предельно возможная разрешающая способность деталей ВЧР.¹⁴⁾

ФИЛЬТРАЦИЯ В ОБЛАСТИ ВРАЩАЕМОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ [20]

При работе в области ПФ приходится ограничиваться линейными инвариантными к сдвигу (ЛИС) операциями, которые могут быть выражены в форме обычной свертки (т. е. в "нулевой области" — в области ВПФ с нулевым угловым параметром). Свертка в области ВПФ не относится к ЛИС-операциям, и в отдельных случаях это обеспечивает большие возможности фильтрации и мультиплексирования, когда их процедуры реализуются в области ВПФ.

В терминах ВПФ временная и частотная оси время-частотной плоскости трактуются как области определения сигнала при а = 0 и при а = п /2. Тогда полное разделение сигнала от шума частотной фильтрацией методом ПФ, т. е. при а = п /2, возможно только в том случае, если спектры сигнала и шума не накладываются. Достаточно простое разделение сигнала и шума при их несовпадении по времени может трактоваться как фильтрация при а = 0. Однако, если ВЧР сигнала и шума занимают промежуточное положение (рис. 2), то их разделение возможно только фильтрацией в области а -ВПФ а = п /4, а частотное разделение (методом ПФ) или временное разделение неэффективно. В другом более сложном случае (на рис. 3 он представлен схематично) выделение сигнала из шума не может быть достигнуто ни частотным методом ПФ ни временным разделением, но может быть эффективно выполнено поочередной фильтрацией в области ВПФ с а = 0, а = п /4 и а = п /2.

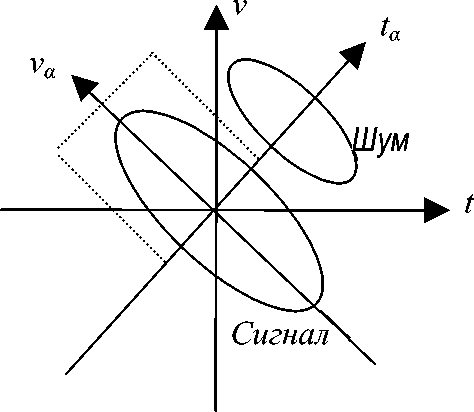
Рис. 2. Разделение сигнала и шума фильтрацией в области а -ВПФ

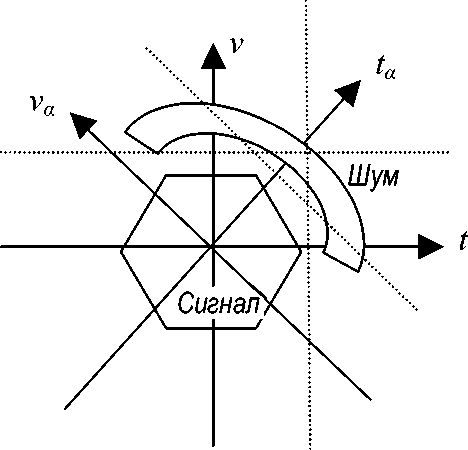
Рис. 3. Разделение сигнала и шума методом повторной фильтрацией в области а -ВПФ при а = 0, а = п /4 и а = п /2

Преимущества фильтрации в области ВПФ (ВПФ-фильтрации) шире, чем показано на рассмотренных примерах с различной конфигурацией ВЧР_ВВ сигнала и шума. Даже в случае частичного наложения этих распределений при ВПФ-фильтрации получается восстановление сигнала с близкой к минимальной среднеквадратичной ошибкой.

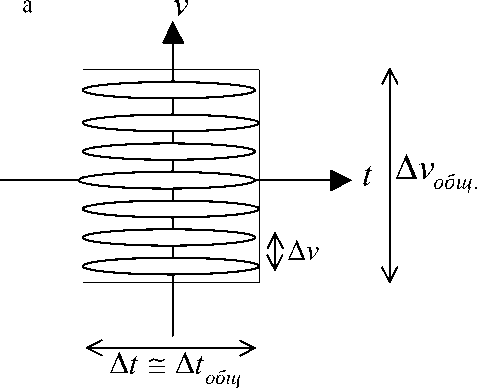
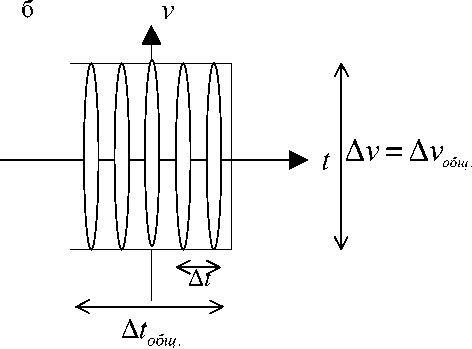
Рис. 4. Мультиплексирование в частотной (а) и временнóй (б) областях. Сигналы показаны своими время-частотными распределениями

МУЛЬТИПЛЕКСИРОВАНИЕ В ОБЛАСТИ ВПФ

Процедура мультиплексирования в частотной или временнóй области (при передаче в канал) состоит в объединении в пакет группы сигналов, которая компактна в этой области. Пакеты сдвигаются друг относительно друга так, чтобы они не накладывались и легко восстанавливались после приема; передача пакета может сопровождаться модуляцией содержащихся в нем сигналов. Отражение процедуры мультиплексирования в частотной и временнóй областях показано на рис. 4 для двух видов конфигурации группы сигналов, представленных своими ВЧР_ВВ.

В первом случае предполагается, что сигналы имеют общую длительность ∆ t общ. , а их частотный

v

∆ v общ .

∆ t общ .

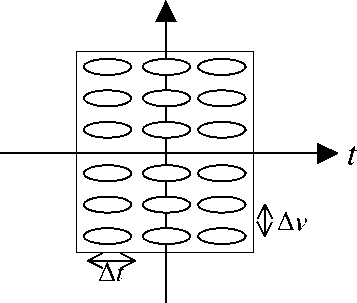
Рис. 5. Совместное мультиплексирование во вре-меннóй и частотной областях. Сигналы показаны своими время-частотными распределениями (ВЧР условно представлены овалами)

диапазон ∆ ν значительно меньше, чем общий диапазон ∆ ν общ. Во втором случае — частотная полоса сигналов равна ∆ ν общ . , а их длительность ∆ t значительно меньше времени ∆ t общ . формируемого пакета, который передается в канал.

В самом благоприятном случае у набора сигналов, подлежащих передаче, ВЧР могут быть таковы, что удовлетворяются оба описанные условия, т. е. ∆ t <<  ∆ t общ . и ∆ ν << ∆ ν общ . . Такой вариант схематично показан на рис. 5. Тогда возможно совместное временнóе и частотное мультиплексирование: производится временной сдвиг ВЧР сигналов (путем свертки с δ-функцией) и частотный сдвиг ВЧР сигналов (умножением их на гармонический множитель e ^{j 2 πν t} ).

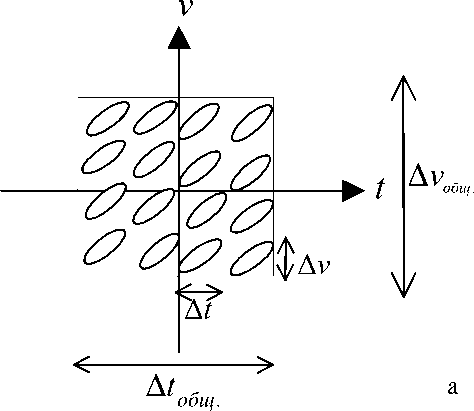
Практически в более часто реализуемых ситуациях ВЧР имеют промежуточную конфигурацию с частичным наложением сигналов и по времени, и по частоте (рис. 6, а). В этом случае более эффективным является мультиплексирование в области ВПФ (рис. 6, б). Угловой параметр α -ВПФ выбирается из соображений симметричного расположения осей 0t α и 0v α относительно ориентации ВЧР набора сигналов, подлежащих мультиплексированию и передаче в канал. В процессе мультиплексирования по этой схеме для упаковки сигналов следует выполнить для них переход в область α -ВПФ с подходящим значением углового параметра. В этой области мультиплексирование осуществляется способом, описанном в пояснении к рис. 5.

tα

∆ t общ

t

∆ v общ .

б

Рис. 6. Неэффективность мультиплексирования сигналов с наложением их ВЧР_ВВ (а) и более эффективное мультиплексирование в области ВПФ (б)

ции, но выполнение их теперь определяется правилами метода ВПФ15).

ЗАКЛЮЧЕНИЕ

Проанализирована трактовка обобщенной модификации преобразования Фурье (ПФ) с использованием операторной формы и концепции собственных функций. Обобщенная модификация ПФ процедурно связана с вращением время-частотной плоскости, называется вращаемым ПФ (ВПФ) и реализуется в новых разновидностях рядов Фурье и ПФ дискретного времени. Рассмотрены соотношения ВПФ с время-частотными преобразованиями, с сигналами с быстро изменяющейся частотой (СБИЧ), возможности ВПФ при мультиплексировании и фильтрации нестационарных сигналов в ИИС.

• ■    Показана взаимосвязь ВПФ с время-частотными преобразованиями общего вида, с преобразованием Радона и с сигналами типа СБИЧ. Проанализирована специфика сигналов (в области их частотно-временной структуры), при которой методы ВПФ могут оказаться более эффективными сравнительно с традиционными способами мультиплексирования и частотной фильтрации.

• ■    Собственными функциями оператора ВПФ с угловым параметром а (оператора а -ВПФ) является ортонормированный набор { Т n ( t )} n = ₁₂₃ функций Эрмита-Гаусса

^Т n ⁽ t ) = -f—Hn ( V^{2 n} t ) exp ( ^{- n} t ²) ,

V2 nn !     V                    '

а соответствующий набор собственных значений — Д = ( j )   } n=1,2Х.. .

• ■    ВПФ имеет два вида интегрального представления с ядром: одно представление использует фактическое значение угла а вращения время-частотной плоскости, второе использует приведенное значение углового параметра ф = а /( п / 2).

Процедура мультиплексирования с использованием поворота время-частотной плоскости может быть обобщена [20] на сигналы, у которых ВЧР не указано. При этом достаточно выполнить сдвиг ВЧР сигналов в подходящем направлении (в области преобразования Вигнера) и сделать это так, чтобы достичь наиболее эффективной упаковки. Как отмечено выше, сдвиг в направлении t включат умножение на 8-функцию; сдвиг по v включает умножение на гармонический множитель. Сдвиг области ВПФ включает те же опера-

• ■    Результат время-частотного преобразования Вигнера—Вилле (ВЧП_ВВ) трактуется как распределение энергии в координатах "время и частота". Применение ВЧП_ВВ к α -ВПФ сигнала эквивалентно вращению ВЧП самого сигнала на угол α (аналогичным свойством обладают и другие ВЧП класса Коэна при условии инвариантности к повороту формирующего ядра преобразования). Дополнительные свойства ВПФ отражены в следующих двух пунктах:

свертка двух сигналов в области ВПФ соответствует свертке (по временнóй переменной) двух ВЧР_ВВ самих сигналов;

умножение двух сигналов (или свертка их ПФ) соответствует свертке (по частотной переменной) двух ВЧР_ВВ самих сигналов.

• ■    Еще одно свойство ВПФ связывает его одновременно с ВЧП_ВВ и с преобразованием Радона ( RAD ψ ). Результат применения оператора Радона к ВЧП_ВВ сигнала эквивалентен квадрату модуля ВПФ этого сигнала для приведенного значения углового параметра.

• ■    Показана схема введения ограничения области определения ВПФ и области ВЧР_ВВ с поворотом время-частотной плоскости. Простейшая форма ограничения — это использование прямоугольного окна. Сокращение области определения по одной оси ведет к ее уширению по другой оси.

• ■    Для ряда ситуаций мультиплексирование и фильтрация осуществляются более эффективно в области ВПФ, чем позволяет выполнение этих процедур традиционными методами — временным или частотным. Это показано путем представления динамики частотной структуры сигнала и шума в области ВЧП_ВВ и вращения время-частотной плоскости.

• ■    Отмечена возможность применения ВПФ к двумерным сигналам (типа изображения) и реализации такого ВПФ оптическими методами.