Метод обобщенных источников в трехмерном сопряженном пространстве

Данная работа является продолжением исследований по применению метода обобщенных источников [1, 2] для различных базисных решений. Метод представляет собой абстрактную схему решения электродинамических задач. Его можно описать как последовательность двух шагов. Первый шаг заключается в выделении некоторой базисной среды, характеризующейся пространственным распределением диэлектрической проницаемости Eb(r) и допускающей точное аналитическое решение электродинамических уравнений Максвелла, для любого распределения токов. На втором шаге различия между исходной и базисной структурами необходимо представить в виде обобщенных токов

^Jgen^{(,) =} -^Ш ⁽Е ^- Eb) E ,                                   (1)

на. основании чего записывается неявное уравнение

E = Einc + ^К [-гю ^{( e — E}b) E ],                              (2)

в котором Ei_nc есть внешнее заданное поле, а К — оператор базисного решения.

Ранее метод обобщенных источников был развит для базисного решения в виде тензорной функции Грина, свободного пространства, в трехмерном координатном представлении [3] и двумерном фурье-представлении [4, 5]. Разработанные методы применимы для расчета, рассеяния на трехмерных уединенных объектах и дифракционных решетках соответственно. При этом численные методы удалось сформулировать таким образом, что их вычислительная сложность является линейной по числу узлов применяемых сеток. Естественным продолжением данных исследований является формулировка, метода, в трехмерном сопряженном пространстве. Ниже приведена, указанная формулировка, обсуждается вычислительная сложность метода, и возможные его приложения.

Базисное решение в трехмерном сопряженном пространстве

Рассмотрим рассеивающую электромагнитное излучение структуру, ограниченную конечным объемом V. Пусть пространственное распределение диэлектрической проницаемости в объеме V задано функцией е(г), а диэлектрическая проницаемость окружающего пространства постоянна и равна еь- Для простоты изложения положим магнитную проницаемость равной постоянной проницаемости вакуума цо- Тогда, как известно, уравнения Максвелла для монохроматических полей с частотой ш и соответствующим временным множителем exp( —гш!) можно свести к уравнению Гельмгольца для электрического поля Е(г), решение которого записывается в виде интегрального уравнения [6]:

E (r) = E j„_c( r ) + гшр, о

( Gь ( г - г ’) J ( г ‘)

J v'

dV ‘

с тензорной функцией Грина Gb (г — г’) = [1 + (1/кь) VV] дь (г — г’). Здесь кь = ш^еьЦо — волновое число волн в однородном пространстве, окружающем рассматриваемый объем, а скалярная функция Грина записывается как дь (г — г’) =

exp(гк_ь | г — г ‘|) 4л | г — г ‘|

Рассмотрим уравнение (3) в трехмерном фурье-пространстве, а именно: получим на основании (3) уравнение для фурье-гармоник Е_ак электрического поля Е_а ( г ), где а = x,y,z, а волновой вектор фурье-гармоник к = (к_ж, к_у , к_г). На основании

Е_ак =

1 (2л)3

J Е_а ( г ) exp (—г кг ) dV

имеем

Е_ак = Е^Г + гшцо f dV exp (—г кг ) [ [^g + 1- (VV)^ дь ( г — г ’) Jg ( г ‘) dV ‘ = v ‘           ^кь

= ЕХ +       / (кь§«р — к_ак_р ) exp (—г кг ’) дь (к) Jg (/) dV ‘ .

кь Jv ‘

Фурье-образ функции Грина (4) есть [6]

^{д ь (к)} = ^2 — к²

+ лг5 (к² — к2) ,

где символ Р обозначает интеграл в смысле главного значения. Подставляя (7) в (6), получаем

Е_ак = / ■ + ^Щ^⁰ (кь5_ад — к_акд ) [Рк2"—Д2 + " (к² — к²^ Jg_k . (8) Уравнение (8) есть базисное решение К метода обобщенных источников для произвольного распределения источников.

Неявное уравнение в трехмерном сопряженном пространстве

Имея уравнение (8) в качестве базисного решения, можно перейти ко второму шагу метода обобщенных источников и подставить токи вида (1) в (8). На этом этапе необходимо рассмотреть два случая: когда е(г) есть непрерывная функция координат и когда эта функция имеет поверхности разрыва, соответствующие границе раздела различных сред. Такая необходимость возникает в связи с невозможностью определить произведение обобщенных функций, имеющих общие точки разрыва, возникающего во втором случае для тангенциальных к границе разрыва компонент электрического поля (подробное описание аналогичного случая приведено в [5]).

Когда функция е( г ) непрерывна, можно перейти к фурье-представлению (1), так что

^Jk = ^{— гш}^ь ^{[(е/ е}ь ^{— -)} * E lk ,                                 (9)

где в правой части стоит свертка фурье-образов соответствующих функций, обозначенная символом «*». Тогда, подставляя (9) в (8), приходим к неявному уравнению для фурье-гармоник компонент электрического поля:

^Еак = ^Еа_к ^{+ (к}ь5аР ^{— к}а^кД ) [^Р 22   /.2 ^{+ Лг}^ (^к2 ^{— к}2)] [   ]   * ^ЕДк‘,       (10)

к — кь                       £ь кк‘ в котором Де = е(г) — еь — дельта-функция Дирака.

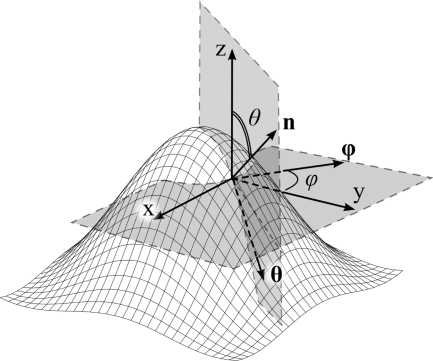
Рис. 1. Введение локальной системы координат п фд на поверхности раздела различных сред, определяемой углами ф и д

В случае разрывной е (г) на границах раздела различных сред необходимо ввести локальную систему координат п фу (рис. 1), как это было сделано в [5], и записать (1) отдельно для нормальных и тангенциальных к границам компонент векторов:

3 \\ к = -i^Eb

Де

- Еь - кк'

* ^Е \\ к'

j ± k = —гшеь

[£ J-1

* Е д к’,

(И)

где символ «— 1» обозначает обращение операции свертки. Тогда, учитывая формулы преобразования векторов (45) и (46) работы [5] из исходной декартовой системы координат в систему пфу и обратно, можно записать:

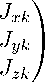
— гше_ь<

Д1

^е ь кк

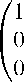
0 \                 )   /Ежк"

⁰ I + Окк' * ^Га^к' к’’   * I ^Еук"

— 1/                   )    \Егк''

Здесь введены следующие обозначения:

^О кк' =^[& ^]-1—[ t L

( sin² ф cos² д sin² ф sin д cos д sin ф cos ф cos д

sin2 ф sin д cos д sin ф cos ф cos д sin2 ф cos2 д sin ф cos ф sin д sin ф cos ф sin д       cos2 ф

В последнем выражении углы, задающие локальную систему координат на границе раздела сред, следует рассматривать как функции декартовых координат.

Подстановка (12) в (8) дает уравнение, заменяющее (10) в случае композитной среды:

Е_ак =Ек + (кь5_аР — к_ак₀ ) ^2 —7 25 + "^л (^к2 - ^кь )] ^х

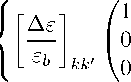
—1

+ ^Окк' * ^Гарк ' к'   *

^Ехк'' ^Еук " . ^Егк ^п

Таким образом, (10) и (17) представляют собой искомые уравнения в трехмерном фурье-пространстве.

Численный метод

В предыдущих работах по методу обобщенных источников удавалосв формулировать быстрые численные методы за счет принятия условия равномерности сетки в координатном либо в фурье-пространстве. Точно так же можно поступить и в рассматриваемом случае. При этом следует иметь в виду, что равномерность сетки в сопряженном пространстве автоматически влечет периодичность в координатном пространстве.

Дискретизация (10) и (17) на равномерной сетке приводит к тому, что почти все свертки становятся матричными умножениями с теплицевыми матрицами. Так, вводя индексы п и т, нумерующие фурье-гармоники, уравнение (10) можно переписать в виде системы алгебраических уравнений на неизвестные амплитуды гармоник компонент электрического поля:

ат

=о - чаев

а0тп

Т7 тс

^Рп ,

где I — единичная матрица, К — блочно-диагональная матрица, а [А е / е ^ ] ^— трехмерная теп-лицева матрица. Решение (16) с помощью итеративного метода, как, например, метода би-сопряженных градиентов или обобщенного метода минимальных невязок, может быть осуществлено с линейной сложностью относительно числа точек сетки в фурье-пространстве. Это обусловлено тем, что умножение на каждой итерации метода может выполняться посредством быстрого преобразования Фурье (БПФ) благодаря теплицевой структуре обращаемой матрицы (подробнее см. [3-5]).

В отличие от (10), уравнение (17) содержит операцию, обратную свертке, которая после дискретизации преобразуется в обращение матрицы [ е ^ /А е ] в (13). Поэтому, чтобы применить аналогичный описанному быстрый численный алгоритм, необходимо произвести дополнительное преобразование матриц:

ат

I - K

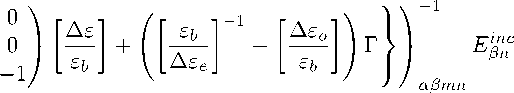
■([АЕ;^]-K{(⁰⁰ 0)[АЕ;]^[ 7 1^{+ ( i -[} й ][ 7 ^])г})    ^[АЕ-^] '

0 0 -1

\             х \          /                                              / артп

Заключение

В результате применения метода обобщенных источников с базисным решением в виде функции Грина однородного изотропного пространства в фурье-представлении (7) были сформулированы уравнения, описывающие дифракцию монохроматического электромагнитного излучения в трехмерно-периодической пространственно неоднородной диэлектрической среде. Показано, что полученные системы линейных алгебраических уравнений (16) и (17) могут быть решены с помощью метода, обладающего линейной сложностью относительно числа узлов сетки в фурье-пространстве. Разработанный метод может быть применен для анализа искусственных периодических структур, как, например, фотонные кристаллы.

Работа выполнена при частичной финансовой поддержке ФЦП «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса

России» на 2007-2013 годы (16.513.11.3117), ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009-2013 годы (14.740.11.0939) и РФФИ (11-07-12072-офи-м и 10-07-00618).