Метод оценки интенсивности пространственного смешения микроорганизмов в биореакторах непрерывного действия

При конструировании новых и модернизации существующих биохимических реакторов непрерывного действия, а также при решении задач интенсификации биотехнологических процессов большое значение имеет рациональная организация потока реагентов. Данное требование связано с функциональной особенностью микроорганизмов физиологически изменяющиеся в зависимости от своего возраста в процессе перемещения по аппарату [1–3]. В ряде биотехнологических производств процесс получения целевого продукта основывается на взаимодействии изменяющихся, в течение времени пребывания в аппарате, по физическим свойствам и функциональным возможностям микроорганизмов с изменяющимся по составу производственным субстратом, причем эти изменения взаимозависимы и носят направленный технологический характер [4–6]. При этом важно, чтобы линейные скорости реагентов данного двухфазного потока системы «субстрат – микроорганизмы» были сбалансированы, то есть приближались к равенству. Такой структуры потока, именуемой «поршневой поток», можно добиться при исключении продольного перемешивания движущейся суспензии, которое может возникать как из-за микротурбулентностей от взаимодействия с элементами конструкции аппарата, так и по причине ламинарного конвективного перемещения слоёв двухфазной суспензии. [7] На практике создать идеальный поток полного вытеснения вязкой жидкости в пространстве, ограниченном твёрдыми стенками, невозможно из-за возникающих касательных напряжений у стенок и молекулярной диффузии. В связи с этим при анализе и математическом описании приближенно поршневого потока применяется диффузионная модель структуры потока.

Смешение микроорганизмов значительно отличающихся между собой по возрасту отрицательно сказываются на интенсивности биотехнологических процессов. Поэтому оценка степени смешения клеток, находящихся в различном функциональном состоянии может являться ориентиром для принятия организационно-технологических мер и конструкторских решений по устройству аппаратов непрерывного действия [8, 9].

Несмотря на практическую важность вышеупомянутой задачи [2, 10], в решении которой заинтересованы инженеры, биохимики, биофизики, микробиологи и другие специалисты, она до сих пор не решена [11, 12]. Это объясняется тем, что биохимические процессы, реализуемые в аппаратах с моделью потока диффузионного типа, как правило, описываются нелинейными уравнениями в частных производных, регулярный метод аналитического решения которых отсутствует.

Объект и метод

Ниже, предлагается теоретико-вероятностный подход к построению и анализу модели диффузионного потока двухфазной биотехнологической суспензии с целью оценки интенсивности смешения микроорганизмов с различным временем пребывания в реакторах непрерывного действия. Для этого используется математический аппарат диффузионного марковского процесса [12].

Будем исходить из уравнения Фоккера– Планка [12–16]:

д    ,              д    ,     .        д¹    ,     .

• — Y ( x , t ) + ^у ( x , t ) = D   . y ( x , t )   ⁽¹⁾

дt            дx            д it где y (x, t) — вероятность обнаружить, например, дрожжевую клетку в объеме аппарата g[ x, x + dx ]• S, S - площадь поперечного сечения аппарата; t – время; x – декартова координата, направленная вдоль оси аппарата; ω – средняя по сечению аппарата скорость движения микроорганизмов; D – эффективный коэффициент диффузии (коэффициент продольного перемешивания).

Линейное уравнение в частных производных (1) относится к параболическому типу и для его решения можно применять известные методы [17–19].

Уравнение (1)следует решать при начальных условиях:

Y ( x ,0 ) = 3 ( x ) , y ( 0, t ) = 0

при t >  0 , x g [ 0, да )              (2)

где 3 ( x ) - дельта-функция Дирака.

Решение должно быть неотрицательным, ограниченным на бесконечности и нормированным к единице, т. е.

да

Y ( x, t ) > 0; y ( да , t ) = 0; J Y ( x , t ) dx = 1   (3)

Умножим левую и правую части уравнения (1) на xⁿdx и проинтегрируем по x от x = 0 до x = да . С учетом (2) и (3) не представляет труда получить систему уравнений для определения момента n -го порядка:

d (x”) = Цxn-1) + п (п -1) (x-2 ) D, dt                                            ,   (4)

п = 1,2,3...

Решение данной задачи известно. Со-

гласно [19]оно таково:

w ( x , t )

•j 2 nDt

г

Г dz ^

exp

- exp

( x - Z ) ²

4 Dt

( x + Z ) 2

4 Dt

exp

2 D

® z (11)

где знак ... означает среднее значение указанной в угловой скобке случайной величины.

Из (4) при п = 1 и п = 2 имеем

Зная функцию w ( x , t ) , из выражения (8) найдем P ( x , t ) :

P ( x , t ) =

.       I dZ ^ exp

^IDD t 0

( Z - x + ro x ) 2

4 Dt

{x ^ = to t , ст 2 = x x ² ^ - xx 2 ² = 2 Dt = ст 2 • xx 2 ² , (5)

- exp

( Z - x + ro x ) 2 _{+ Ю} 1 4 Dt    ⁺D ’ ■

где ( x ) и ст ² - соответственно среднее значение и дисперсия распределения случайной величины x ; ст 2 = 2 D/ Ц x^ .

В дальнейшем нам понадобится явный вид как функции у ( x , t ) , так и функции P ( x , t ) = J у ( y , t ) dy .

Очевидно, что функция P ( x , t ) удовлетворяет уравнению

Правую часть выражения (12) можно преобразовать к удобному для вычисления виду:

P ⁽ x . t > - 2 ]

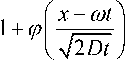
,     ( x - to t

1 - ^ 1

rax exp D

^ ,(13)

где ^ ( Z ) - интеграл вероятности ^ ( 0 ) = 0,

д ,     .        д ,     .        д²     ,    ,

— P ( x , t ) +      P ( x , t ) = D—P ( x , t ) , (6)

д t            д x            д it

^ ( ±да ) = ± 1.

Далее,     так как

начальному и граничному условию вида

P ( x ,0 ) = 1 , x >  0 ; P ( 0, t ) = 0 , t >  0      (7)

д

Y ( ^x , t ) = —^P ( ^x , t ) , д x

имеем:

то из

по определению выражения (13)

Преобразуем уравнение (6) к более простому виду. С этой целью произведем замену искомой функции по формуле:

^{Y ( x} ■ t ^)- v ; ? Dr ^exp

( x - to t ) 2

4 Dt

-

P ⁽ x , t ) = w ^{( x} , t ) exp 1 ^{Ц -} "' t , 2 D 4 D

to

2 D

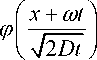
exp _D

ra x

где w ( x , t ) - новая неизвестная функция,

подлежащая определению.

Подставив выражение (8) и (6) с учетом (7), получим уравнение для определения функции W ( x , t )

дд

— w (x, t ) = D    w (x, t), д tд

где функцию w (x, t) следует подчинить нижеследующему начальному и граничному условиям w (x,0) = exp ^-Ц^; w (0, t) = 0, t > 0. (10)

Зная функцию у ( x , t ) , перейдем к вычислению степени смешения микроорганизмов P , где P – доли сосуществующих клеток, поступивших в аппарат с входным потоком жидкости соответственно t и t часов назад ( t и t – времена пребывания микроорганизмов в аппарате).

Пусть γ – функция для двух «времен наблюдения» t = t_Y и t - 1 ₂, где t ₂ >  t_Y , - известна. Графики функций у ( x , t 1 ) и у ( x , 1 ₂ ) представлены на рисунке 1, где x = x_p - точка их пересечения, которую аналитически можно найти из решения уравнения:

у ( ^x P , t 1 ) = у ( ^x P , t 2 ) ⁽¹⁴⁾

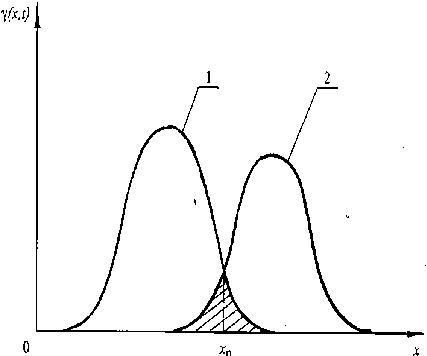
Рисунок 1. График функции γ = (x, t) при t = t 1 (1) и t = t 2 (2) для определения степени пространственного смешения микроорганизмов

Figure 1. The graph of the function γ = (x, t) for t = t 1 (1) and t = t 2 (2) for determining the degree of spatial mixing of microorganisms

Величину x найдем из решения уравнения (14). Для сг₀ <  0,2с погрешностью менее одного процента:

xP

Подставляя данное значение x в выражение (15), с учетом (12), получим расчетную формулу для определения величины P

_ . /t X — 1 )

Ps = 1 - Ф

2   ^{2 D}

° "0 =   27

<у t]

° 0

2 D

.

Пример: пусть t ₂ = t_x ( 1 + n ° ) , где

Тогда из выражения (17) получим

n >  0.

PS =1 - Ф

n

Заштрихованная площадь на рисунке 1 численно равна величине Рs . Из рисунка следует, что xP                      го

P = j у (x, t2) dx + j у (x, tx) dx =

0                x_P                  (15)

= 1 + P ( x p , t 2 ) - P ( x p , t i ) .

При выводе формулы (15) было учтено, что P ( 0, t ) = 0 , P ( го , t ) = 1 .

Результаты и обсуждение

Следовательно, для определения степени смешения микроорганизмов при заданных t и t необходимо знать явное выражение для функции P ( x , t ) и значение величины x_p .