Метод оценки эффективного коэффициента шероховатости в меандрированных руслах на основе численного моделирования

DOI:

Динамика русловых течений существенно зависит от морфологии канала [1]. В гидродинамическом моделировании крупномасштабные характеристики рельефа учитываются в явном виде [2]. Для оценок пропускной способности русел в гидрологии часто используется модель Шези, в которой коэффициент сопротивления может определяться уравнением Маннинга [3]. Эта формула связывает скорость потока с поперечным сечением канала, учитывая свойства подстилающей поверхности. При данном подходе принято считать, что влияние параметров русла определяется коэффициентом шероховатости. Для расчета коэффициента Маннинга существует большое количество формул, справедливых для частных случаев, их вывод основан на натурных наблюдениях и лабораторных экспериментах [11; 12].

Особый интерес для исследования представляет влияние извилистости русла на коэффициент Маннинга [7; 10]. В реальных условиях выбрать значения величины очень сложно. В данной работе представлен метод оценки шероховатости меандрированного русла, основанный на численном гидродинамическом моделировании.

Численная модель

В основе численной модели лежит система уравнений Сен-Венана, которая описывает динамику русловых течений в приближении теории мелкой воды и учитывает влияние рельефа, внешних и внутренних сил, а также работу источников [4; 6]. Для интегрирования системы уравнений используется CSPH-TVD метод [5] и подход распараллеливания на основе CUDA-технологии [9].

Рассчитать скорость руслового потока можно при помощи формулы Шези [3]

V_av = C ( IR )^1/2,                                            (1)

где V – средняя скорость потока; C – коэффициент Шези; I – гидравлический уклон; R – гидравлический радиус. Для определения коэффициента C существуют различные формулы. Наиболее часто используют формулу Маннинга

C = R ^1/6/ n ,                                              (2)

где n – коэффициент шероховатости по Маннингу [с/м^1/3], который является составной величиной и учитывает свойства подстилающей поверхности дна. Обозначим n ₀ – основное значение коэффициента шероховатости в прямолинейном русле; n_m – эффективный коэффициент Маннинга в меандрированном канале. В численной модели параметр n используется при расчете силы придонного трения.

В качестве модели прямолинейного русла зададим функцию b0(x, y) = –bmax exp(y2/L2) – Ix                                 (3)

с базовым набором параметров b _max = 5 м; L = 500 м и уклоном I = 0,07 м/км. Для меандрирован-ного русла профиль дна зададим в виде

b ( x , y ) = – b _max (exp(( y – y _max sin( kx ))²/ L ²)) – Ix ,                          (4)

где k определяет пространственный масштаб меандрирования; y _max – амплитуда меандра. Выберем значения k = 2π/3 500 (1/м); y _max = 1 200 м, 2 400 м. При указанных параметрах отношения длин меандрированного русла к прямолинейному равно 1,75 и 2,95 соответственно. На входе расположим источник воды с суммарным расходом Q = 1 500 м³/с, время расчета t = 3 сут.

Результаты расчетов

Для оценки влияния извилистости русла на параметр n проведем расчеты на меандри-рованных руслах с n ₀ = 0, а для прямолинейного канала величину n ₀ будем варьировать. На рисунке 1 приведена структура стационарного потока на гладком прямолинейном рельефе для участка 5 000 м ≤ x ≤ 18 000 м.

Распределение глубины и скорости для меандрированного русла с y _max = 1 200 м изображено на рисунке 2. В этом случае мы можем наблюдать неустойчивость потока при малых значениях n . Этот эффект возникает и в прямолинейном канале [8].

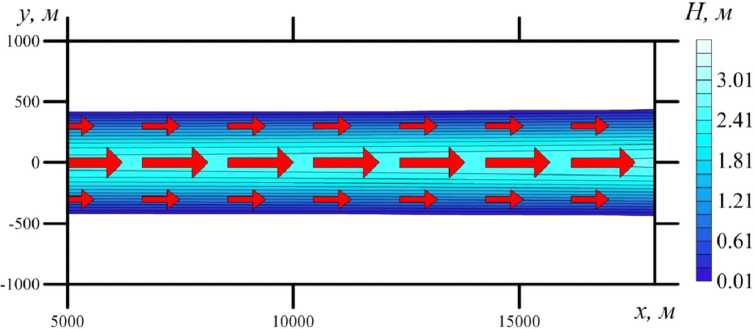
Рис. 1. Распределения глубины и поля скоростей потока в прямолинейном русле при n ₀ = 0,02

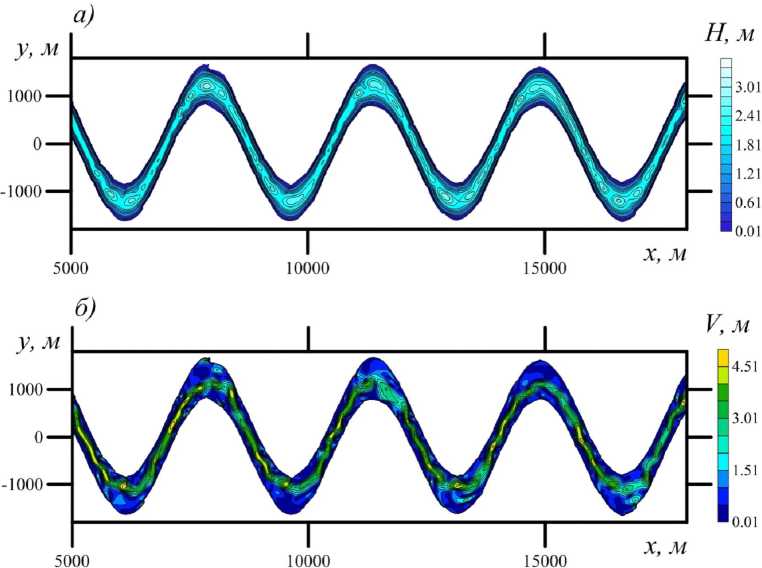
Рис. 2: а – распределение глубины меандрированного участка; б – распределение модуля скорости

Определим среднюю скорость потока в сечении канала через интегральный расход воды Q

< V > = Q/S ,

где S – площадь сечения.

На основе серии расчетов, проведенных на рельефе b ₀( x , y ) со значениями n ₀ = 0,01 ÷ 0,05, получим зависимость < V > от n ₀ (см. рис. 3). По построенной аппроксимации можно определить значение n_m . Для меандрированного канала с амплитудой y _max = 1 200 имеем n_m = 0,0175 (см. рис. 3, точка A ), в случае y _max = 2 400 м коэффициент n_m = 0,048 (см. рис. 3, точка B ). Как видим, при увеличении амплитуды меандра в два раза значение эффективного коэффициента Маннинга увеличивается в 2,7 раза и зависимость не является степенной.

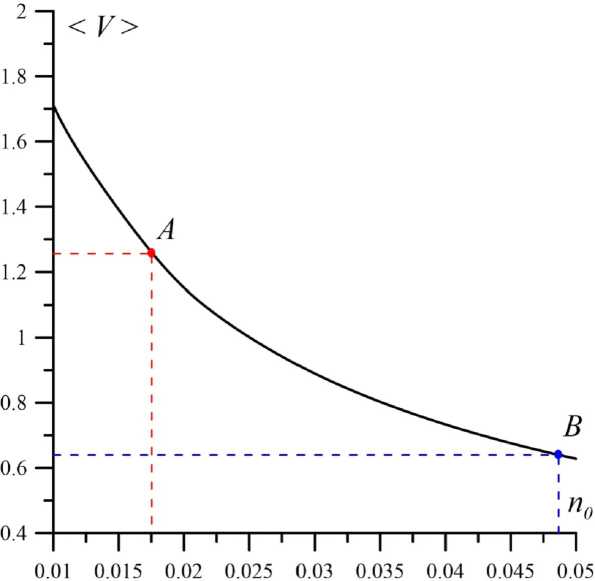
Рис. 3. Результат аппроксимирующей зависимости средней скорости в сечении русла <  V > (м/с) от коэффициента Маннинга в прямолинейном канале

Заключение

Для определения вклада в сопротивление потоку от меандрированного русла в работе предложен метод определения эффективного коэффициента Маннинга n_m . Наш подход основан на сравнении результатов численного гидродинамического моделирования в меандрированном и прямом руслах. С усилением степени извилистости русла имеем уменьшение средней скорости движения жидкости в сечении канала. Варьируя основное значение коэффициента Маннинга n ₀ в прямом канале на основе численных гидродинамических моделей, мы оценили вклад в сопротивление потоку от меандрирования русла.