Метод оценки предельных значений дисперсии нестационарных случайных сигналов

Дисперсия нестационарных случайных сигналов типа переходный режим (НССПР) на выходе ЛДО в переходных режимах от включения стационарных случайных воздействий (ССВ) рассчитывается как интеграл двойной свертки:

tt aS( t) = aB J ho (y )J ho (x )P( y - x) dx, (1) 00

где a S - дисперсия ССВ; р - нормированная корреляционная функция (НКФ) ССВ; h_О – импульсная характеристика ЛДО. Для ИХ любых ЛДО и р , описываемых экспоненциально-косинусными функциями, (1) вычисляется с помощью табличных интегралов. Функция a S ( t ) асимптотически стремится к установившемуся значению a yст = a S ( да ) >  0, а при некоторых сочетаниях ИХ и НКФ и их параметров имеются выбросы над a yст [1]. Предельным значением a S max может стать a yст (для монотонных aS ( t )) или наибольший выброс. Однако аналитическое определение наличия выбросов, их значений и, следовательно, нахождение предельных значений дисперсии затруднено необходимостью решения трансцендентных уравнений при поиске экстремумов функции aS ( t ).

В работе ставится задача разработки универсального численного метода оценки предельных значений a S max .

• 1.    Метод аппроксимации

Интеграл (1) исходной формы может быть вычислен по одной из двух частей области интегрирования внутреннего интеграла [2] и тогда (1)

примет вид:

t

t

aS (t) = aS J ho (y) J ho (x)р(y - x)dx + J ho (x)р(y - x)dx о 10                         y ty

= 2 a S J ho ( y ) J ho ( x ) р ( y - x ) dx .

Далее полученный двойной интеграл может быть представлен [2] интегралом произведения ИХ и функционала F ( у ):

t

^ S ⁽ t ) = ² ^ В J h o ⁽ у ) F ⁽ у ) dy ,                     ⁽²⁾

y

F ( У ) = J h o ( x ) р ( У - x ) dx -                     ⁽³⁾

о

Вид функционала F ( у ) совпадает с реакцией ЛДО на детерминированное воздействие, описываемое функцией вида р ( x ) . Это обстоятельство дает возможность оценить сверху функционал F ( у ) и с помощью полученной оценки разработать численный алгоритм, который позволит вычислить оценки текущих предельных значений НССПР в виде непрерывной или кусочно-непрерывной функции, удовлетворяющей условию:

t

^ S max ⁽ t ) ^ ² ^ В J h O ⁽ у ) F ⁽ у ) ^dУ •

В работах [3, 4, 5] рассчитан модуль максимума максиморума реакции ЛДО на ограниченное по модулю детерминированное воздействие. Так как функция р ( x ), входящая в F ( у ), также ограничена по модулю, то примененный подход пригоден также для расчета оценки F _max ( у ), следовательно, и для расчета ^ S _max . Метод [3], использует форму записи реакции ЛДО, соответствующей несколько иному виду функционала F ( у ):

y

J h_o ( у - x ) р ( x ) dx .

о

Поэтому подробнее остановимся на формуле (3). Подынтегральное выражение в (3) представляет собой произведение двух функций h_o ( x ) и р ( у - x ). Рассмотрим графики функций, входящих в (3), при этом функция р ( у - x ) аппроксимируется функцией р * ( у - x ), которая должна максимизировать F ( у ).

В общем случае h_o ( x ) - знакопеременная функция (рис.1, сплошная линия). Функция р * ( у - x ) (также, как и в [3]) для знакопеременной ИХ имеет ступенчатый вид: р * ( у - x ) = ± 1 (рис.1, пунктирная линия). Изменения знака р * ( у - x ) на противоположный в моменты изменения знака h_o ( x ) обеспечивают максимальные по модулю (максимизируют) значения F ( у ). Заметим, что такой вид функции р * ( у - x ) аппроксимирует знакопеременную НКФ.

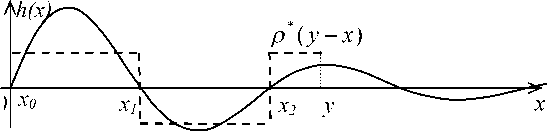
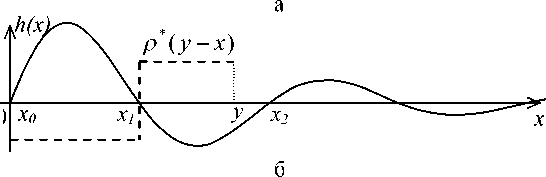
Рис. 1. К расчету оценки предельного значения F ( у ) для различных верхних

пределов интегрирования у

Необходимо учесть, что НКФ р (у - х ) произвольной формы, в отличие от произвольного детерминированного воздействия в [3], в точке х = у всегда имеет значение, равное +1 и поэтому

Р *⁽ У ^{- х} )| х = у = ^{+ 1}- ⁽⁴⁾

Отсюда следует, что текущее значение Fmax (у) имеет тот же знак, что и знак ho (х)| х=у на текущем интервале знакопостоянства ИХ - на тех интервалах, где ho (х) х=у >0 (см. рис.1а) Fmax(у) >0, а на интервалах, где hO (х)| х=у <0 (см. Рис.16) Fmax (у) <0, т-е

F max ⁽ у ) = ‘

M - 1 ^х j + ¹                 у

£ J hO (х)|dх + J hO (хW, hO (х)| х=у > 0, j=0 хj              хм

M - 1 ^х j + ¹                 у

^ J h o ^{( х} ) dix ⁺ J h o ^{( х} ) ^dх , h o ^{( х} )|

( j = ° X j              х_м          )

х = у

< 0.

Границы интервалов интегрирования X j в (5) являются нулями ИХ h_o ( х ), которые находятся аналитически для знакопеременных ИХ типовых ЛДО не выше 2-го порядка или численно для знакопеременных ИХ ЛДО выше 2-го порядка; ( M - 1) - число полных интервалов знакопосто-янства ИХ на интервале от 0 до х = у .

Таким образом, функция (5), как численный аналог интеграла (3), по модулю представляет собой максимизированный функционал (3) и позволяет получить приближенную оценку F_max ( у ).

Функция Fmax (у) непрерывно возрастает по модулю и в конце произвольного M -го текущего интервала знакопостоянства ho (x)| x=у (при у = xM+i) текущее значение модуля Fmax (у) достигает максимума на дан ном интервале:

F М max

M x j ^{+ 1}

E J h o ^{( x} )| ^dx , h o ⁽ x )| x = у >  0, j = 0 x j

—

x

M x j ^{+ 1}

E J h o ^{( x} )l ^dx , h o ^{( x} )

< 0.

x у

j = 0 x

У j    x j

Вычисленные таким образом FM max являются оценками сверху модуля функционала F ( у) на произвольном M -м интервале знакопостоянства

ИХ и по модулю совпадают с [3], при этом знак FMmax совпадает со зна ком ho(у) на M -м интервале знакопостоянства ИХ.

Далее оценка сверху дисперсии (2) вычисляется раздельно для каждого интервала знакопостоянства ИХ h_o ( у ), где F ( у ) заменяется оценками

FMmax , вычисленными с помощью (6). Поскольку знаки FMmax и ho (у) на любом интервале знакопостоянства ИХ совпадают, то вычисляемая оценка

^{2 a} S max

( M — 1        t j ^{+ 1}

⁽ t ) = ² ^ B E ^F j max J h o ⁽ у ^dУ ⁺ F M max

U=⁰       t j

t                     '

J ho ( у )dy tM—i            7

для любого интервала будет всегда положительной и приобретает вид монотонно возрастающей функции без локальных максимумов и минимумов.

Таким образом, универсальный численный алгоритм вычисления оценки (7) позволяет достаточно просто и инвариантно к НКФ оценить сверху дисперсию для любого ЛДО.

Для вычисления оценки F _max ( у ) в случае знакопеременной ИХ и зна-копостояннной НКФ последнюю следует аппроксимировать иначе (рис. 2, пунктирная линия), исключив отрицательные значения функции р (у — x ), т.е. р (у — x ) —+ 1.

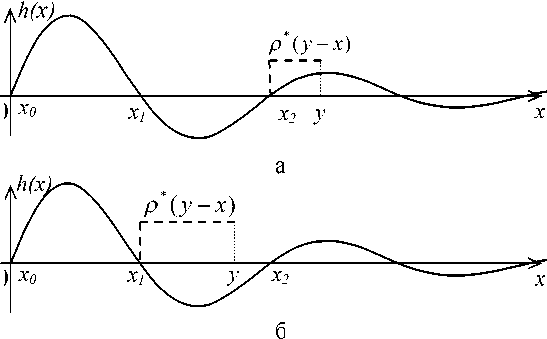
Рис. 2. К расчету оценки предельного значения F ( у ) для знакопостоянной НКФ

Тогда, с учетом вышеизложенного, F_{M max} примет вид:

F М max

x j + 1

J h0o (x)dx, ho (x)| x=у > ° xj xj+1

- J h o ⁽ x ) dx , h o ⁽ x )| x = у <  ⁰

x j

Оценка сверху дисперсии (2) с учетом (8) примет вид:

_ 2

° S max

t j ^{+ 1}                                          t

⁽ t ) = ² ^ j F j max J h O ⁽ У )dy ^{+ F} M max J h o ⁽ У ) ^

x           t j                             t M - 1

\

.

Аналогично (7) оценка дисперсии (9) имеет вид монотонно возрастающей функции без локальных максимумов и минимумов.

Рассмотрим ЛДО со знакопостоянной ИХ. В этом случае функция р (у - x ), максимизирующая F ( у ), примет вид р * ( у - x ) = + 1. Тогда _max ( t ) вычисляется непосредственно по (1) и получим:

^ S max ⁽ t ) = ^ В g О ⁽ t ),

t где

g _О ( t ) = J h_o ( у ) dy - переходная характеристика ЛДО. о

Следует отметить, что оценки (7) и (9) оказываются значительно завышенными и подлежат уточнению следующим образом. На первом интервале знакопостоянства x0 = 0, x 1 = 11 (t1 - граница первого интервала знакопостоянства ИХ); p (y - x) = +1 и тогда x 1

F1max = f ho (x)dx = go (x 1) = go (t1), а текущие значения оценок (7) и (9) о совпадают и равны:

° S max ⁽ t ) = ² ° В g ⁽ t 1 ) g ⁽ t ).

В конце первого интервала знакопостоянства ИХ t = 1 1 и тогда

° S max ⁽ t 1 ) = ² ° В ^g O ⁽ t 1 ) ^.

В то же время для р (y - x ) = + 1 оценка дисперсии на первом интервале знакопостоянства ИХ ЛДО вычисляется непосредственно по (1). Тогда получим следующее значение оценки дисперсии:

° S max ⁽ t 1 ) = ° В g o ⁽ t 1 ) ^.

Если потребовать, чтобы в точке t 1 оценка дисперсии не превышала (11) тогда (7) преобразуется к виду

° S max ⁽ t ) = ° В

M           t j ^{+ 1}

S F j max f h O ⁽ У W ⁺ F M + 1max j = 1             I

V ^j              t j

t

\

f h o ( y ) dy .      (12)

t M + 1

Соответственно оценка (9) с учетом вышеизложенного примет вид:

° S max ⁽ t ) = ° В

'            t j + 1

F j max f h O ⁽ У )dy ⁺ F M max

V         t j

t

\

f h o ⁽ y ) dy .      ⁽¹³⁾

t M - 1

Полученные оценки (12) и (13) также имеет вид монотонно нарастающих функций без локальных максимумов и минимумов и содержат взвешенные суммы интегралов от ИХ на интервалах знакопостоянства. Весовые коэффициенты представляют собой сумму интегралов от модулей ИХ или интегралы от модулей ИХ по интервалам знакопостоянства.

Численный расчет оценок (12) и (13) позволяет достаточно просто и инвариантно к НКФ оценить сверху дисперсию для ЛДО любого вида и любого порядка.

На основе описанного численного метода оценки предельных значений дисперсии нестационарных случайных сигналов разработана универсальная методика приближенной оценки границ динамического диапазона НССПР и его производной, которая заключается в следующем:

• а)    для знакопостоянных ИХ предельная оценка текущих значений дисперсии (дисперсии производной) рассчитывается как (10);

• б)    для знакопеременных ИХ и знакопеременных НКФ:

• -    определяются границы интервалов знакопостоянства ИХ;

• -    для каждого интервала знакопостоянства рассчитывается предельные значения F_im.,_x согласно (6);

j max                 v / *

• -    для каждого интервала рассчитывается предельная оценка текущих значений дисперсии согласно (12);

• в)    для знакопеременных ИХ и знакопостоянных НКФ:

• -    для каждого интервала знакопостоянства ИХ рассчитывается предельные значения F j _max согласно (8);

• -    для каждого интервала знакопостоянства рассчитывается предельная оценка текущих значений дисперсии согласно (13).

• 2.    Пример расчета оценки предельного значения дисперсии

Рассмотрим пример, который иллюстрирует применение разработанной методики приближенной оценки границ динамического диапазона НССПР для ИХ и НКФ, имеющих относительно простой вид.

На вход ЛДО, описываемой ИХ h_o ( t ) = a ²[1 - a t ]exp( -a t ), ( a = 0,1)

подается ССВ с корреляционной функцией

R ( t ) =

( A = 0,0995; в = 0,01).

нВр(т) = нВ | cosAt + —sin2|r| |e V A )

Несмотря на относительно простой вид ИХ и НКФ точное выражения дисперсии, рассчитанное по (1), в сокращенной форме имеет весьма сложный вид:

h S ( t ) = D ₀{ D 1 - [( D ₂ + D ₃ t )sin( A t ) + ( D 4 + D ₅ t )cos( A ))] x

x e 'a+e) t + (D 6 + D 7t + D8t2) e2a}, где D0 ^ D8 - коэффициенты, зависимые от параметров ИХ и НКФ a , А , в . Для выражения (14) определение максимально возможных значений дисперсии значительно затруднено.

Поскольку как ИХ так и НКФ знакопеременные функции, то для применения разработанной методики следует: а) определить границы интервалов знакопостоянства ИХ; б) для каждого интервала знакопостоянства рассчитать предельные значения F_{j max} по формуле (6); в) для каждого интервала рассчитать предельные оценки текущих значений дисперсии по формуле (12).

• а)    Определение границ интервалов знакопостоянства ИХ

Импульсная характеристика h0 (t) = a2 (1 - at) exp(-at) имеет два ин- тервала знакопостоянства, разделенных единственным нулем 11 = 1/ a = 10 (рис.3).

• б)    Расчет предельных значений F j _max

Функционал (6) на 1-м и 2-м интервалах знакопостоянства ИХ примет значение соответственно

1/ a

a

F1max = a2 (1 - ax) exp(-ax)dx = — о                               e

и

Г                        2 a

F 2max = F lmax + a ⁽¹ - a x ) e^XP⁽ a x ) dx =--- • e

1/ a

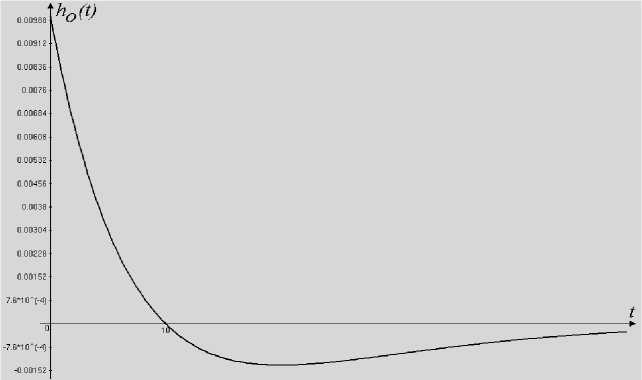
Рис. 3.

в) Расчет предельной оценки текущих значений дисперсии

Оценка дисперсии по двум интервалам знакопостоянства, согласно (12) примет вид:

^s, max ( t ) = "

3 t                                                  3 a                   a — (1 - a x )exp( - a x ) dx = —t exp( - a t ), 0 <  t <  1/ a ; e 0                           e a a        / t = 1/ a ; a 2 ,f 2 a ) , ' fx,      , , —y + 1— l a   (1 - a x )exp( - a x ) dx =                 (15) e ^ e )   1/ a a a , ^{ a 2. , a 1            , = — — + 2 1-- a t exp( - a t ) l , t >  1/ a ; e L e у e                 ) _

3 a ²

—, t ^да . e

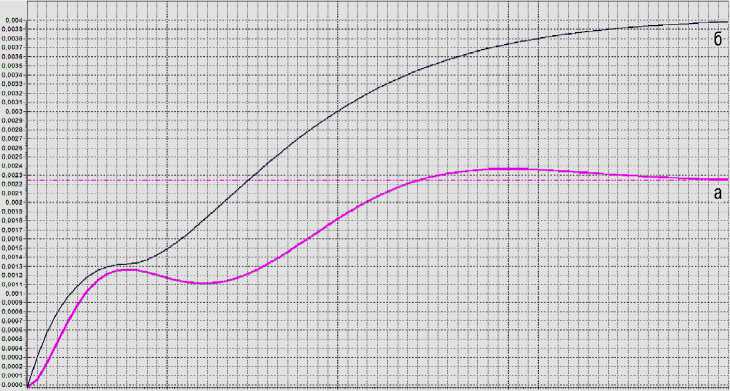
На рис.4 показаны: (а) график дисперсии г г S ( t ), рассчитанной по (14); (б) график оценки предельного значения дисперсии a S _max ( t ), вычисленной по приближенной формуле (15).

О                    10                    20                    30                    40                    50                   60                    70

Рис. 4.

Оценка (15) имеет вид монотонно возрастающей функции несложного вида, которая асимптотически стремится к установившемуся значению 3 a ² / e ² без локальных максимумов и минимумов. Процедура вычисления оценки (15) значительно проще, чем расчет точного выражения дисперсии (14) и поиск по нему точного максимального значения дисперсии.

Поскольку при расчете численной оценки функционала (3) аппроксимирующая функция ρ ^* ( y - x ) не учитывает затухающий характер НКФ, оценка σ _S ²_max ( t ) предельного значения дисперсии с течением времени возрастает быстрее, чем дисперсия σ _S ²( t ) .

Заключение

Разработан численный метод оценки предельных значений дисперсии нестационарных случайных сигналов типа переходный режим. На основе разработанного численного метода создана универсальная методика, которая позволяет получить в простой форме, с невысокими вычислительными затратами оценки предельных значений дисперсии нестационарных случайных сигналов типа переходный режим, инвариантные к виду корреляционной функции воздействия.