Метод описания течения и определения реологических констант вязкопластических биоматериалов. Часть 1

К вязкопластическим биологическим средам, демонстрирующим одновременно вязкие свойства и порог текучести, относятся как многокомпонентные жидкости, подобные крови [1,2], так и относительно твердые ткани внутренних органов. Так, по мнению авторов, вязкопластические модели могут привлекаться и для феноменологического описания формоизменения (движения) тканей и органов в условиях структурных изменений адаптационно-компенсаторного характера при силовом воздействии. К ним следует отнести костную ткань [3] и пародонт зубочелюстной системы [4], выполняющие опорную и соединительную функции. Для указанных биотканей имеет место ярко выраженный пороговый характер адаптивной реакции. Так, например, «вязкие» перемещения зуба при ортопедической коррекции, вообще говоря обусловленные процессами резорбции и остеогенеза, инициируются при определенном уровне механических напряжений. В целях биомеханического описания важно получить определяющие соотношения подобных объектов и на их основе определить соответствующие реологические константы.

Следует отметить, что изучением подобных сред занимались многие исследователи [5-11]. В большинстве случаев [8-11] полученные результаты относятся либо к модели нелинейной вязкой жидкости, имеющей нулевой предел текучести, либо описывают среду Шведова-Бингама с единичным коэффициентом скоростной чувствительности. Однако одновременный учет порогового напряжения и нелинейной вязкости биоматериалов в соответствии с механической моделью, показанной на рис. 1, очевидно, имеет принципиальное значение, что и является предметом настоящего исследования.

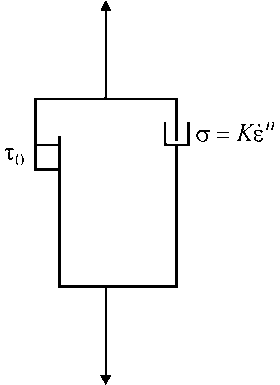
Рис. 1. Механическая модель нелинейной вязкопластической среды.

Анализ экспериментальных данных по реологии крови

Экспериментально показано, что кровь является существенно нелинейной вязкопластической средой [1,2]. Механическая нелинейность крови обусловлена ее сложным составом, в особенности, наличием фазы гематокрита, состоящей из эритроцитов (красных кровяных телец) в плазме. Пластичность крови обусловлена вращением, дисковой формой , деформацией и ориентацией эритроцитов, образованием и распадом эритроцитных агрегатов в виде «монетных столбиков» в процессе течения. Неньютоновский характер течения крови, выявляемый в ротационных вискозиметрах, также объясняют агрегацией и морфологией эритроцитов. Важно, что реологические свойства крови существенно различаются при их измерении вискозиметрами куэттовского и пуазейлевского типов по сравнению с in vivo [1].

Сказанное свидетельствует о том, что течение крови неудовлетворительно описывается зависимостями, предложенными для ньютоновской жидкости с постоянной вязкостью ц = const, например, формулой Пуазейля для течения в капилляре

_ 4л

π r Δ p µ

где Q - объем кровотока; r , 1 - радиус и длина капилляра; A p - перепад давления; ц -вязкость. В связи с этим рассмотрим более точные вязкопластические модели и возможность аппроксимации последних для описания течения биологических сред.

Зависимость напряжений сдвига т от скорости сдвига Y для стационарных течений учитывает формула Кессона

Vr"=7^т 0 + k   ,                                  ⁽²⁾

где Т о - предельное напряжение сдвига; к - кессонова вязкость.

Метод «эффективной вязкости»

В работе [6] рассмотрен метод исследования пространственных течений вязкопластических сред с единичным коэффициентом скоростной чувствительности, основанный на введении «эффективной вязкости». Показано, что данный метод в первом приближении может быть применен для описания течений Куэтта и Пуазейля.

В настоящей работе показано, что для существенно нелинейных сред данный метод имеет невысокую точность и его следует применять с большой осторожностью.

Полные уравнения Г. Генки, описывающие пространственные течения вязкопластических сред [10], не удается решить из-за существенно нелинейной зависимости тензора напряжений от тензора скоростей деформации. Часто делают некоторые предположения относительно поля скоростей и применяют полуобратный метод, как это было проделано в работе [7], или используют замену уравнений течения вязкопластических сред уравнениями течения вязких жидкостей (уравнениями Навье-Стокса). В этом случае возникает проблема выбора коэффициента вязкости среды.

Целью данной работы было выяснение, применим ли данный метод к существенно нелинейным средам, и идентификация констант вязкопластической среды т о , n , K в условиях течения Пуазейля при известном расходе и перепаде давления.

Описание вязкопластической модели биоматериалов

Для общего теоретического описания биоматериалов предлагается следующий путь перехода от уравнений Генки к уравнениям Навье-Стокса для нелинейных вязкопластических сред.

Имеем следующие определяющие соотношения [9]:

S ij ² — ^ j ;

j                 mm                                                         (3)

i 1

т = т о + K I    I при т>т о ( Н = 0 при т<т о ),

V^s о )

где S ij - девиатор тензора напряжений, ^ ij - девиатор тензора скоростей деформации, К - пластическая вязкость, т о - предельное напряжение сдвига, m - параметр скоростной чувствительности.

Здесь предлагается проводить линеаризацию следующим образом. Комплекс [х m -1 1

— I заменяется параметром  n e, который предлагается называть s о )

«эквивалентной вязкостью» рассматриваемой вязкопластической среды:

т„      И m - 1

n_e=^ r + K ^— ---.                            (4)

e H     ( s _о ) m

С физической точки зрения эта замена означает, что факторы предельного напряжения сдвига и вязкости вязкопластической среды заменяются некоторой эквивалентной вязкостью. Следовательно, под эквивалентной будем понимать вязкость ньютоновской жидкости, оказывающей такое же сопротивление своему относительному перемещению, что и данная вязкопластическая среда.

Предлагается определять эквивалентную вязкость, как характеристику данного течения, следующим образом.

Будем считать, что определяемая из (4) величина ne не зависит от переменных интегрирования. В этом случае система уравнений движения вязкопластической среды будет описывать течение вязкой ньютоновской жидкости с коэффициентом динамической вязкости, равным n e• Определяем поле скоростей и давлений данного течения, а также интенсивность скоростей деформаций. Подставляя найденное значение интенсивности скоростей деформации в (4), получим в общем случае трансцендентное уравнение относительно ne• Решая его, найдем эквивалентную вязкость как функцию времени и пространственных координат. Используя далее различные способы осреднения, найдем n e как некоторую характерную величину процесса, не зависящую от переменных интегрирования.

Точное решение задачи о движении нелинейной вязкопластической среды

Ниже приводится точное решение задачи о движении нелинейной вязкопластической среды в круглом цилиндрическом капилляре при стационарном перепаде давления.

Для нашего материала имеем определяющие соотношения (3). Уравнения движения среды в трубе (в цилиндрической системе координат r , ф, z ) имеют вид:

<

дс rr	+	1	дс r ф	+	дс rz , с rr		—с
д r		r	дф		д z		r
дс ф r	+	1	дс ФФ	+	дс ф z	+ 2 с...
д r		r	дф		д z	r
дс zr	+	1	дс z ф	+	с zr +	дс zz	,
д r		r	дф		r	д z

+ р F = р a ф ;

р Fz =р az, фф

— + р F_r =р a_r ;

где с ij - компоненты тензора напряжений, ( F_r , F _ф , F_z ) - вектор массовых сил.

Задачу будем решать полуобратным методом. Относительно поля скоростей сделаем следующие предложения: V_r = 0; V ф = 0; V_z = V_z ( r ). При данных предположениях тензор скоростей деформации имеет следующий вид:

г =             =0- £ =0- £ =0- £ = 17’ s rr V; s r ф V; sфф V; sфz V; S zz U; s rz 2 (r )•

Из определяющих соотношений следует запись тензора напряжений:

с? = ^c j

P p

0 —

⁰    ° rz

V ° rz

p

0 —

•

p 7

С учетом (6) имеем следующие уравнения движения

д p л

= о и д r

d°zr , °zr dp с rr______      _ dp dp          A p _ _

—zr- +— zr- + -f- = 0. Предположим также, что = const = о с dr r dz                                       dz           l ^zr

—

A p ——r a 2 l , а

~ h с c iap интенсивность тензора напряжений т = J-^ SijSy = -^ | r, интенсивность девиатора тензора скоростей деформации Н = 27ij ^ij = Vz(r) •

Тогда из определяющих соотношений для интенсивностей:

1 A p 2 l

^r = Т о + K

( Wr )

m

V ^{s 0}

1 1 ^A Р I _r

2 l

—

n

T I -SO-

4) I , ⁰ 7 K n

где n = — •

m

Поскольку V_z ( r ) убывает при

стоять минус. Далее считаем, что

r > a, то Vz (r) < 0 и перед скобками должен sо = 1*с-1, поэтому в формулах эту величину опускаем.

Из условия прилипания рассматриваемой среды к стенкам капилляра имеем V z ( a ) = 0.

V ⁽ r ) = - K Tj [ 2^ Tr ^{— T} 0) dr = ^C 1

J 2l__ ^f 1 M

Kⁿ |A p\ ( n + 1 ) ^ 2 1

A ^{n + 1}

r ^T 0

J

V, ( a ) = 0 э C 1

1       21 f 1 |AP|        A a - T

K" |A p\ ( n + 1 ) ( 2 1       ⁰ J

В итоге получим следующую формулу:

V z ⁽ r ^{) =}

1       2 l

K " |A p\ ( n + 1 )

f 1 l^A P l 1 ^{2 1}

A ⁿ + ^{1 a -T} 0

J

f 2 ^ r

n + 1

^{— T} 0

J

Находим радиус

1 1^A p l 2 l

r ₀

2t₀ 1

=^T 0 ^ r ⁰ "|A P| ’

области зон что совпадает

застоя из условия т ( r ) = Т 0 .  Тогда

с радиусом зон застоя для линейных

вязкопластических сред [6].

Вычислим расход среды Q в произвольном сечении капилляра:

a                   r 0

Q = J 2 п rV z ( r ) dr + J 2 n rV z ( Г 0 ) dr , r 0                    0

где V z ( r 0 ) - скорость движения среды в зоне застоя.

После подстановки скоростей в (11) и интегрирования получим:

Q =

----------2= 1 ----------f¹ lA P l a

K IA p\ ( n + 1 )( n + 2 )( n + 3 ) ( ^{2 1}

\ n + 1

^-T 0 J

{ ( n + 1 )( n + 2 ) a ² + 2 r ₀ ² + 2 ar^ ( n + 1 ) } . (12)

При n = 1 получим известную формулу Букингэма [8]:

Q = —ⁿ^-\ ^{f 1} — ^P a - t ^A ( б a ² + 2 r ₀ ² + 4 ar ₀ ) ,

K |A p 3 • 4 ( 2 1       ⁰ J ^{v 0       07}

после преобразования которой получим:

n d ^{4   A} p li  4 r 0   1 f r 0 A 4

Q 16 K • 8  1  I    3 a   3 ( a J I , где d = 2a – диаметр капилляра.

Пример расчета параметров течения

Рассмотрим решение методом эффективной вязкости задачи о течении пластической среды через сечение капилляра при стационарном перепаде давления.

В соответствии с вышеуказанным порядком определения эквивалентной вязкости находим вначале решение соответствующей задачи для вязкой жидкости с динамическим коэффициентом вязкости ηе. Воспользовавшись, например, решением, приведенным в [8], запишем:

V z =

L dp ( r П /77 '

⁴ n e ^dz

—

r

dV z dr

—

1 dp

2 П e ^dz

r .

Здесь

dp dz

– постоянный перепад давления, R – радиус сосуда, r – текущая

радиальная координата (ось z направлена вдоль центральной оси). Находим интенсивность скоростей деформации

H =

dV dz

2 П e

dp dz

r .

Cреднее значение интенсивности скоростей деформации по радиусу области вязкопластического течения вычисляется по формуле:

< H > =

R f Hdr = 1^-

R - ro J       4П e r0

dP ( R + r o ) .

Подставляя в (4) среднее значение Н из (16), получим уравнение для определения эквивалентной вязкости. Уравнение имеет следующий вид:

П e

Ц ( 4 П . ) m ^{- 1}

dp

dz

m - 1

( R + r o ) ^{m - 1} +

^{4 т} 0 П e

dp dz

( R + r o )

Отсюда следует, что в области вязкопластического течения r o <  r <  R выражение для скорости V_z ( r ) имеет вид

/ х (д^{m -1} ^ m

V ( r ) =|⁴--- I

I ^ J

dp, ⁽ R ^{+ r} 0 ^{)- 4 r} 0

⁽ R ^{+ r} 0 )

1/ m

( r ² - r ² ) .

В интервале r o <  r <  0,5 R приближенная оценка, вычисленная методом эффективной вязкости, отличается от точной не более чем на 30% для любых нелинейно-вязкопластических материалов. Для объемного расхода имеем формулу

Q = тП I dp 1 ( R - r )" ⁺¹ 1 ¹ ( R ² + r 2 ) ) ,               (19)

ⁿ ( 4 ^ ) ” 1 dz P ^o) 1 2^{V      o} J                    ^{v 7}

что совпадает с приближенной формулой, приведенной в работе [6].

Чтобы сравнить, насколько величина расхода, определяемая по приближенной формуле отличается от расхода, определяемого точной формулой, оценим относительную погрешность:

/ . X n + 1 /        \

| A Q\   ( 2 J    ^{( 1 +} k ² >(^{n + 1 )(n + 2 )(n + 3 )}

Q ( n + 1 )( n + 2 ) + 2 k ² + 2 k ( n + 1 )

При n = 1 величина расхода (19) совпадает с формулой, приведенной в [6], и максимальная погрешность достигает 12,1% при k = 0,41, что дает достаточно надежную расчетную оценку. Однако с увеличением n погрешность растет и при n = 4 достигает 60%, т.е. для существенно нелинейных вязкопластических сред приближенная зависимость (19) расхода оказывается неприменимой.

Выводы

Метод «эффективной вязкости» может быть применен в задаче определения момента в условиях течения Куэтта. В особенности, если вязкая составляющая существенно больше пластической, в первом приближении вязкопластическое сопротивление может быть описано в терминах «эффективной вязкости». При сравнимых величинах µH m /ε 0 и τ 0 применение метода не гарантирует нужной точности.

Для течения Пуазейля метод “эффективной вязкости” может быть применен при n , близком к единице, и при достаточно большом перепаде давления. Для существенно нелинейных материалов, когда значение n близко к 0,25, метод неприменим.

При идентификации нелинейного вязкопластического материала обнаружено, что при малых τ ₀ ( τ ₀ < 0,3 К ) процесс нахождения τ ₀ неустойчив. При τ ₀ > 0,5 К погрешность не превышает 10%, остальные константы ( n , K ) вычисляются со значительно более высокой точностью.

Разработанная модель учитывает реологические свойства крови и может быть использована для уточненного описания гемодинамических процессов.