Метод описания течения и определения реологических констант вязкопластических биоматериалов. Часть 2

В первой части [1] данного исследования было показано, что для уточненного описания механических свойств ряда биологических материалов следует привлекать модель вязкопластической среды с нелинейной вязкостью. В частности, разработанная в [1] методика такого описания может быть использована для определения реологических констант крови при течении в артериях и капиллярах и пищевых субстратов при движении по кишечному тракту с образованием квазитвердой области, а также кинетики деформирования мягких тканей организма, демонстрирующих квазипластичность вследствие выраженного порогового эффекта по отношению к нагрузке (например, остеогенеза и резорбции зубных тканей при ортопедической коррекции зубного ряда).

Знание реологических констант крови необходимо для описания гемодинамических явлений [2], диагностики заболеваний [3] и разработки протезов сосудов. Целью настоящей работы было определение реологических констант крови при помощи эксперимента, имитирующего кровоток на масштабном уровне мелких вен и артерий, играющих важную роль в функционировании сердечно-сосудистой системы (табл. 1).

Таблица 1

Параметры изучаемых сосудов (средние значения)

Вид сосуда	Диаметр, см	Длина, см	Количество
Артерии	0,1	10	600
Вены	0,06	1	1800

Таблица 2

Зависимость вязкости крови µ (с ⋅ П) от скорости сдвига при содержании гематокрита Н =44.8 %

Скорость сдвига, у , с-1
0,1	0,3	0,7	1,0	4,0	7,0	10,0	35,0	70,0	100,0
95	60	37	30	20	14	10	8	6	5

Таблица 3

Условия гемодинамических испытаний

Скорость поршня, мм/мин	60	120	180	240	360
Скорость течения в капилляре, м/с	0,7	1,4	2,1	2,8	4,2

Методика эксперимента

При проведении эксперимента учитывалась выраженная скоростная чувствительность механических характеристик крови как структурированной среды в виде суспензии эритроцитов в плазме [4]. Ранее было показано [2], что в зависимости от скорости сдвига наблюдается феномен упругого деформирования крови (при весьма малых значениях у), затем имеет место вязкопластическое течение и далее -ньютоновское течение с постоянной вязкостью. Трудности определения предела текучести крови при малых скоростях сдвига у ^ 0 обусловлены миграцией эритроцитов от стенок вискозиметра. При высокой скорости сдвига кровь ведет себя как ньютоновская жидкость с постоянной вязкостью, что описывается простейшей зависимостью т = цу , Ц = const. (1)

Эти особенности реологии крови были выявлены на ротационном вискозиметре, реализующем куэттовское течение гомогенной среды, когда ширина зазора между соосными цилиндрами прибора во много раз превышала размер эритроцитов. В соответствии с данными, приведенными в таблице 2, вязкость крови изменяется в широких пределах в зависимости от скорости сдвига.

Таким образом, в основном диапазоне скоростей сдвига уравнение состояния крови должно соответствовать вязкопластическому закону течения, причем этот диапазон расширяется при увеличении содержания гематокрита Н . Можно предположить, что вязкопластические свойства проявляются и в условиях течения Пуазейля через канал цилиндрической формы (капилляр), что более характерно для сосудистой системы.

Рис. 1. Способ реализации пуазейлевского течения крови

Тест на растяжение

Удлинение (мм) б

Удлинение (мм)

в

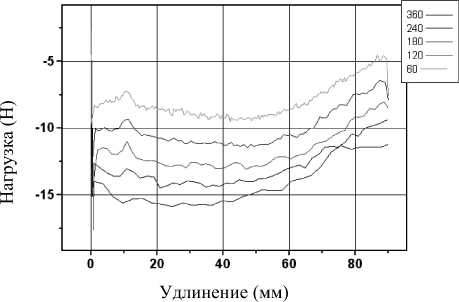
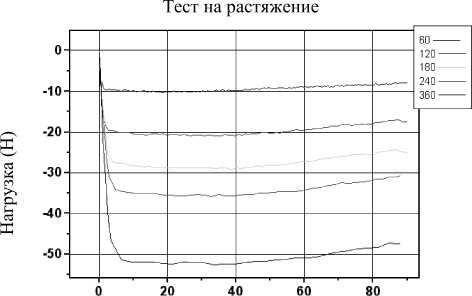
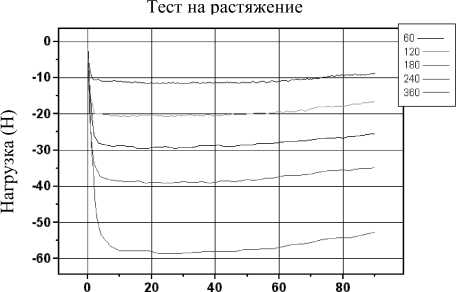
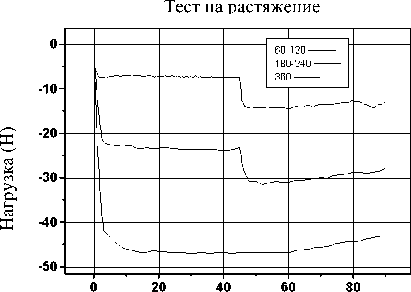
Рис. 2. Зависимости гемодинамического сопротивления от перемещения: а – испытания при незаполненном цилиндре; б, в – испытания при постоянной скорости; г – испытания при ступенчатом изменении скорости

Удлинение (мм) г

В частности, в настоящей работе изучение реологических свойств крови проводилось по схеме, показанной на рис. 1.

В отличие от обычно используемых стандартных вискозиметров [5] в качестве нагружающего и силоизмерительного устройства применяли универсальный испытательный стенд INSTRON 5567 ( UK , 2002), обеспечивающий прецизионное определение усилий и перемещений при стабильной скорости нагружения. Нагнетание крови в капилляр производилось при помощи медицинского шприца емкостью 60 мл и диаметром поршня 26,5 мм, установленного в зажимах стенда. Максимальный ход поршня устанавливался равным 90 мм.

Имитатор сосуда представлял собой прямолинейный отрезок тонкой трубки (капилляр) длиной 180 мм из бионейтрального полимера, используемого при изготовлении катетеров для ангиографии, и соединялся со шприцем при помощи стандартного адаптера. Внутренний диаметр имитатора составлял 1,0 мм.

Нужно отметить, что в силу степенной зависимости расхода от данного параметра важно обеспечить высокую точность измерения диаметра капилляра. Кроме того, материал имитатора имеет существенно более высокую жесткость по сравнению с биотканью сосудистой стенки и его дилатация (увеличение диаметра) под действием давления крови незначительна. Для более адекватного моделирования кровотока необходимо корректировать диаметр, учитывая нелинейное деформационное поведение стенок эластичных кровеносных сосудов.

Для исследования использовалась R -масса (получаемая из цельной крови путем отделения плазмы методом центрифугирования), которая до измерения хранилась в холодильнике при низкой температуре. Измерение сопротивления кровотоку через капилляр для каждой скорости нагнетания производилось с использованием свежей порции крови. Испытания проводились при температуре 37° С для пяти значений скорости поршня и соответствующих значений скорости течения в капилляре, обратно пропорциональных отношению квадратов диаметров поршня и капилляра (табл. 3).

Результаты испытаний приведены на рис. 2 (отрицательный знак регистрируемого усилия соответствует сжатию шприца в стадии нагнетания). С целью устранения систематической погрешности, обусловленной трением поршня о стенки цилиндра, на каждой скорости предварительно проводилось нагружение в условиях смачивания стенок без заполнения цилиндра (рис. 2а). При этом имели место незначительные флуктуации усилия, вызванные, очевидно, изменениями условий трения поршня в цилиндре. Измеренное усилие трения вычиталось из регистрируемых усилий при заполненном цилиндре и тем самым выделялась компонента гемодинамического сопротивления. Для каждой скорости испытание повторялось 3 раза. Было также проведено испытание с изменением скорости нагнетания в середине рабочего хода, что позволяет выявить динамику переходного процесса (рис. 2г).

Зависимости гемодинамического сопротивления от времени для указанных скоростей приведены на рис. 2 б–г. Видно, что происходит достаточно быстрая стабилизации регистрируемого усилия, а с ростом скорости течения гемодинамическое сопротивление увеличивается.

Идентификация вязкопластической модели

Полученные экспериментальные данные были использованы для идентификации гемодинамической модели, основанной на решении задачи о течении вязкопластической среды через капилляр при стационарном перепаде давления для следующих определяющих соотношений [1]:

т •

i    H bj, <Т = Т0 + K(H) , Т > Т0 ,                             (2) 18 0 ) H = 0, т < то , 1 где Sij – девиатор тензора напряжений, τ – интенсивность напряжений сдвига, Н – интенсивность скоростей деформации; ξij – девиатор тензора скоростей деформации, К – пластическая вязкость, τ0 – предельное напряжение сдвига, m – параметр скоростной чувствительности, 80 - характерная скорость деформации (параметр, определяющий размерность).

Расчет проводился путем решения системы нелинейных алгебраических уравнений

2n l         ( 1 ^Д рД

----------------------------- —J----1 a

^ " | Д р , |( n + 1 )( n + 2 )( n + 3 ) ( ²   /

X n +1

- т 0     { ( n + 1 )( n + 2 ) a ² + 2 r ₀ ² + 2 ar₀ ( n + 1 ) } = Q i ,

)

2τ l где r0 = -j—0- - радиус квазитвердой области; Др - перепад давления; ц, n, т0 -0    Др\     r J                                                                         и реологические константы;

dp dz

– градиент давления, a , l – радиус и длина капилляра,

k = r ⁰; Q i - объемный расход среды в единицу времени, i = 1, 2, 3. a

В соответствии с полученными экспериментальными данными были найдены следующие значения реологических констант τ ₀ =0,58∙10^-3 Па, k =0,89∙10^-2 Па, n =1,111. Таким образом, кровь является нелинейной вязкопластической средой, хотя и с весьма малым пределом текучести.

Оценка точности расчета была получена при помощи дополнительного эксперимента. В частности, проведение контрольного теста при скорости кровотока в капилляре 2,8 м/с показало, что относительная погрешность расчета τ ₀ , n , k не превышает 1%. Кроме того, результат расчета τ ₀ согласуется с известным пределом текучести крови для высоких (более 40%) значений гематокрита.

Заключение

Проведенное расчетно-экспериментальное исследование подтверждает вязкопластическое поведение крови. Разработанная методика может быть использована для определения реологических констант крови в условиях артериального и венозного течения.