Метод определения in vivo вязкоупругих характеристик скелетных мышц

Биомеханика спорта является новым и быстроразвивающимся направлением в стыковой области технических наук (механика), биологии (структура и свойства живых тканей, органов и организма в целом) и педагогики (средства и методы тренировок). Исходя из актуальности практических рекомендаций для спорта высших достижений, важно разработать способы оценки адаптации опорно-двигательного аппарата человека к экстремальным физическим нагрузкам. С этой целью авторы считают необходимым: 1) разработать метод определения макроскопических (вязкоупругих) характеристик мышц по результатам неинвазивных испытаний; 2) описать деформирование мышечных тканей при генерации усилий (актуации) и определить критерии утомления мышечных тканей на мезоуровне, т.е. в масштабе отдельных мышечных волокон. Это позволит связать данные нагрузочно-скоростных режимов, выполняемых спортсменами на имеющихся тренажерах, с биофизическими механизмами актуации, утомления и релаксации мышечных тканей.

В настоящее время при обосновании режимов тренировок и реабилитации спортсменов стремятся определить показатели тонуса мышц при различных нагрузках. Основными экспериментальными методами подобного исследования мышечной активности в настоящее время считаются изометрическое и изотоническое электростимулирование [1, 2]. Их существенным недостатком является инвазивность. Кроме того, имеет место неправомерность переноса свойств, определенных в указанных тестах, на мышечную ткань живого организма. Следовательно, необходимы новые методы, позволяющие адекватно оценивать механические свойства мышц.

Значительные диагностические возможности могут быть реализованы путем более полной интерпретации результатов динамического индентирования мышц мобильными автоматизированными приборами [3–8], применяемыми в спортивных и медицинских учреждениях. В указанных методиках используется корреляция диаграмм вдавливания и растяжения, отмеченная, в частности, в работе [9]. В частности, для определения тонического напряжения, эластичности скелетных мышц и т.д. прибором «Миометр UT 98-01» (Эстония) [8] производят контактное деформирование исследуемой мышцы или ее части с регистрацией биомеханической реакции при помощи устройства, схема которого показана на рис. 1.

Предварительно в области диагностируемой мышцы производят прижатие к кожному покрову индентора массой m = 20 г на площади S = 7,07 мм², что приводит к статической реакции, уравновешивающей силу тяжести mg. Индентору практически мгновенно придается начальная скорость движения v 0 по нормали к поверхности. Динамическая реакция вязкоупругой биоткани вызывает затухающие колебания без нарушения контакта. Посредством встроенного акселерометра регистрируется и передается в компьютер зависимость ускорения от времени a ( t ) (рис. 2).

Выходными являются следующие параметры:

• •    частота F (Гц), которая определяется как величина, обратная промежутку времени между вторым и третьим максимумами ускорения индентора;

• •    декремент D в виде натурального логарифма отношения второго максимума ускорения к третьему;

• •    жесткость H (Н/м), равная отношению максимальных значений силовой реакции биоткани к максимальному внедрению индентора, определяемых для этапа колебания без учета предварительного прижатия.

Указанные параметры, полученные для расслабленной и напряженной мышцы, позволяют оценить тоническое напряжение и эластичность мышечной ткани, а также определить силовой потенциал мышцы, скорость протекания восстановительных процессов и другие характеристики, необходимые для коррекции и оптимизации тренировочных режимов.

Однако получаемые на приборе «Миометр UT 98-01» параметры определяются не только свойствами биотканей, но и условиями испытания (массой и площадью поверхности индентора, его начальной скоростью и т.д.). Следовательно, величины F , D , H не могут рассматриваться как механические характеристики вязкоупругого материала, образующего мышцу. Это обстоятельство снижает информативность известной процедуры миометрии. Целью настоящей работы является создание метода определения вязкоупругих характеристик мышечной ткани на основе экспериментальных данных динамического индентирования мышцы in vivo .

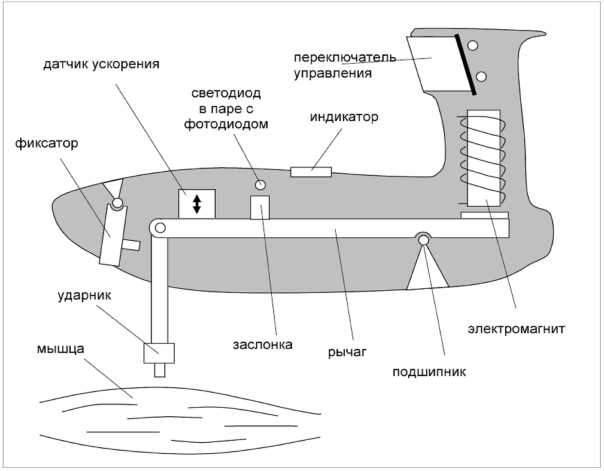
Рис. 1. Схема выносного измерительного элемента прибора «Миометр UT 98-01»

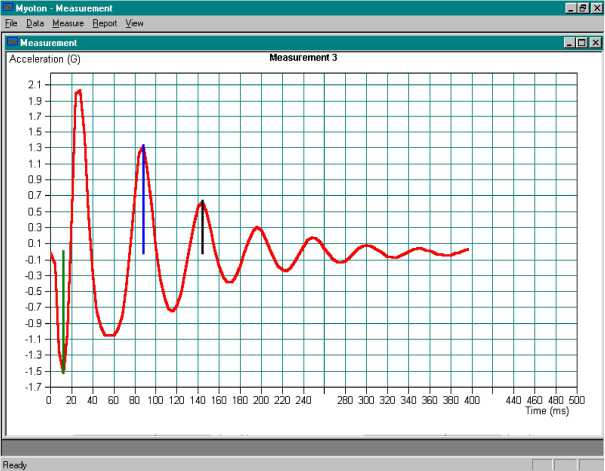
Рис. 2. Характерная зависимость ускорения индентора от времени при испытаниях на приборе «Миометр UT 98-01»

Математическая модель динамического идентирования

Известные подходы к идентификации моделей индентирования биотканей предполагают достаточно сложную математическую процедуру расчета механических параметров, включая конечно-элементное моделирование контакта и решение соответствующей обратной задачи [4, 5]. Можно упростить идентификацию, используя известные аналитические решения. При внедрении жесткого индентора в линейноупругое изотропное полупространство вертикальные смещения точек поверхности полупространства u ( r ) связаны с контактным давлением p интегральным соотношением [10]

и ( F ) =

1 — v2 г г pdS пE Уr-rol’

Здесь E, v - модуль Юнга и коэффициент Пуассона материала полупространства; г0 - радиус-вектор точки полупространства в области контакта. Интегрирование в уравнении (1) производится по площади области контакта. Если индентор имеет плоскую поверхность в виде круга радиусом R, нормальные перемещения точек поверхности контакта одинаковы и совпадают с внедрением индентора и0. Уравнение (1) можно переписать в виде u о

/ / Р ( Г о ). r' ⁸ dr ⁰

^{п E} оо       ^г ² + г _о - 2 гг _о cos 8

Здесь 8 , г о - полярные координаты точки области контакта; г — модуль радиус -вектора точки поверхности полупространства в пределах области контакта ( r изменяется от 0 до R ). Реакция полупространства P определяется суммированием контактных давлений

R

P = ^{2 n}J Р ^{( г} о ) ^г о dr o ’ о

При заданном внедрении и _о уравнение (2) позволяет определить зависимость контактного давления от координаты г _о. Установлено, что в диапазоне изменения радиуса R от 1 до 2 см простая аппроксимация

P = о,638 —^R—Eu _о                           (4)

1 - v ²

дает относительное отклонение от численного решения уравнений (2) и (3), не превышающее 0,07 %.

Коэффициент Пуассона материала мышечной ткани как материала высокомолекулярной природы можно принять равным 0,5. При описании деформационного поведения биотканей необходимо учитывать их реономные свойства (процессы ползучести и релаксации). Будем рассматривать материал мышечной ткани как линейно-вязкоупругий, заменяя модуль Юнга E соответствующим интегральным оператором[11]

t

Ef ( t ) = e f ( t ) - je( t - T ) f ( T ) dT

_ о

Здесь ft ) - произвольная функция времени; 0 ( t ) - ядро релаксации. Наиболее простое экспоненциальное ядро релаксации, позволяющее адекватно описать вязкоупругое деформирование высокомолекулярных материалов [8], имеет вид: 0 ( t ) = Ae ^-e t . Здесь A , в - параметры ядра релаксации. При использовании данного ядра релаксации зависимость реакции от внедрения индентора (4) примет вид

P = к и _о( t ) - A j e ^{в (} t ^{т )} и _о( т ) d т

Здесь введен коэффициент к = о,851 п RE . После дифференцирования равенства (5) по времени и математических преобразований получим

P + e P = kU 0 + ku ₀( P- A ).                           (6)

Здесь точкой над символом обозначена производная по времени от соответствующей величины.

Так как параметры движения индентора на этапе колебания определяются прибором «Миометр UT 98-01» без учета предварительного прижатия (после уравновешения силы тяжести), динамическое уравнение движения индентора имеет вид: P = - mU₀ . Следовательно, уравнение (6) можно переписать в виде

U ₀ +в U "₀ + — \U ₀ + и ₀( Р- A ) ] = 0.                         (7)

m

Начальные условия для внедрения индентора на этапе колебания следующие:

и 0 (0) = 0, U 0 (0) = v 0 , U "0 (0) = 0.                             (8)

Таким образом, движение индентора при динамическом индентировании описывается дифференциальным уравнением третьего порядка с постоянными коэффициентами (7) при начальных условиях (8).

Определение вязкоупругих характеристик

Технически очень трудно создать протез, который способен выполнять все функции кисти человека, поэтому авторы решили акцентировать свое внимание на самой главной функции, подразумевающей восприятие. Решение уравнения (7) будем искать в виде и 0( t) = CeY t.

Для величины у составим характеристическое уравнение

Y ³ + Ру ² + ^— у + ^— ( в - A ) = 0.                         (9)

mm

Анализ экспериментальных диаграмм a ( t ) (рис. 2), полученных при миометрии, позволяет сделать вывод о том, что после придания индентору начальной скорости v 0 его движение принимает характер затухающих колебаний. Следовательно, можно предположить, что два из трех корней уравнения (9) являются комплексно сопряженными с отрицательной действительной частью, а третий корень действительный отрицательный

Y 1 = -р , у 2 =- n - iw, у 3 =- n + iw .                      (10)

При таких корнях характеристического уравнения (9) зависимость u0(t) можно записать в виде u 0 (t) = C 1 e-pt + e -nt \C2 sin(wt) + C3 cos(wt)].

Константы C 1 , C 2 , C 3 определяются из начальных условий. Функция u 0 ( t ), удовлетворяющая начальным условиям (8), определяется следующим образом

^U 0 ⁽ t ) =

v 0

p ² + n ² + w ² - 2 p n

2 ne ^-p t

+ e ^{- nt}

( P 2

2      2

+ w - n

w

sin( wt ) - 2 n cos( wt )

Первое слагаемое в скобках в уравнении (11) оказывает влияние на величину u0 только в течение малого промежутка времени после начала движения индентора. Второе и третье слагаемые в (11) описывают затухающие колебания с циклической частотой w и логарифмическим декрементом затухания n —. Величины n и w связаны w с выходными параметрами F и D прибора «Миометр UT 98-01» следующим образом w = 2пF, n = DF.

Третий определяемый параметр H равен отношению первого максимума силы P к первому максимуму внедрения u 0

H =

P

max

u

max 0

- m

min u ₀

_{u 0} max

Момент времени t 1 , соответствующий первому минимуму ускорения индентора, определяется из условия u 0 ( t 1 ) = 0, которое сводится к уравнению

- 2 n р ³ e ^р t ¹ + — (р ²(3 w ² - n ²) + ( n ² + w ²)² ) e ^{nt 1} sin( wt 1 ) + + ( р ²(3 n ² - w ²) - ( n ² + w²)² ) e - ^{nt 1} cos( wt 1 ) = 0 .

Момент времени t 2 , соответствующий первому максимуму внедрения, определяется из условия u ₀( 1 ₂) = 0, которое сводится к уравнению

- 2 n р e ^-р t ² + e - ^{nt 2}

— ( w ² + n ² - р ² ) sin( wt ₂) + ( w ² + n ² + р ² ) cos( wt ₂) w

= 0.

Тогда выражение для жесткости (13) можно переписать следующим образом

_ 2 _-р t i . - nt р e ^{p 1} + e ¹

р ²( n ² - w 2 ) - ( n ² + w 2 ) 2 .           2 Z x

----------------------------siⁿ⁽ wt 1 ) ^- р co^s( wt 1 ) =

2 nw

-

H

m

e ^-р tt²

+ e ^{- nt 2}

( 2  2,2

р- —+И!

,     2 nw

)

sin( wt ₂ ) - cos( wt ₂ )

)

При известных величинах n и w равенства (14)–(16) составляют систему нелинейных уравнений, позволяющую определить моменты времени t 1 и t 2 , а также параметр р .

Процесс определения параметра р можно существенно упростить, измеряя промежуток времени t 1 до первого минимума ускорения индентора по зависимости u(t ), получаемой на приборе «Миометр UT 98-01» в автоматическом режиме (рис. 2).

При известном t 1 параметр р определяется из условия минимума ускорения u (1 1 ) = 0, которое можно свести к нелинейному уравнению (14). Так, используя выражения (12) и уравнение (14), можно по заданным параметрам F , D , t 1 определить корни характеристического уравнения (9). Следует отметить, что для исследуемых мышц значения параметра р , определенные в результате решения уравнения (14) и системы (14)–(16), практически совпадают, а численное решение уравнения (14) представляется более простой задачей, чем решение системы (14)–(16).

Если известны величины n , w , р , уравнение (9) с учетом равенств (10) позволяет определить искомые вязкоупругие характеристики E , A , в

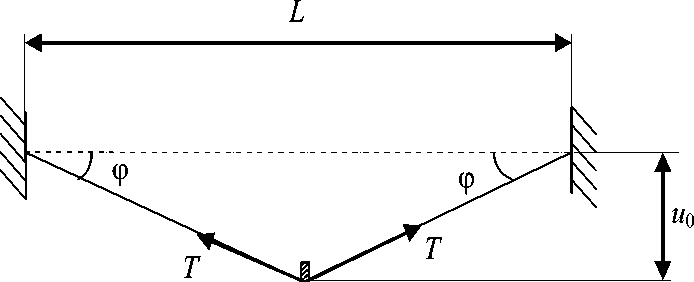
Рис. 3. Прогиб натянутой нити

в _ р ( р 2 - 3 n 2 + w ²) + 2 n ( n ² + w ²) a _ ( в - р ) ( w ² + P 2 + 2 n в - 3 n 2 ) p ² + n ² + w ² - 2 n p       ,            2 n в + w ² - 3 n ²

E _ —- — ( 2 n в + w ² - 3 n ² ) .

0,851 n R^v               ’

Таким образом, для получения вязкоупругих характеристик материала E , A и в необходимо последовательно использовать выражения (12), уравнение (14) и формулы (17).

Характеристики напряженной мышцы

Миометрия используется для определения механических параметров мышцы как в пассивном состоянии, так и при ее активации в изометрических условиях. Характер изменения показателей при переходе мышечной ткани из расслабленного состояния к напряженному позволяет судить об эффективности тренировочного процесса и вырабатывать рекомендации по его оптимизации. Изменение показателей при активации мышцы обусловлено, главным образом, действием растягивающей силы T , совпадающей по модулю с максимальной силой, генерируемой мышцей при изометрическом возбуждении [1]. Наличие силы T приводит к тому, что на индентор при внедрении действует дополнительная сила PT , возрастающая с внедрением u 0 . Для определения силы PT используем аналогию между напряженной мышцей и натянутой нитью (рис. 3).

Для струны PT = 2 T sin ф* 4Tu . Здесь L - длина нити. При контактном индентировании выражение для силы PT будет иметь более сложный вид. Однако характер зависимости PT от силы T и внедрения останется тем же, что и для струны: P_T _ KTTu 0 , где K_T - коэффициент, определяемый геометрическими параметрами мышцы. Используем последнее равенство для силы PT в уравнении (5)

', к+Кт р -«t-')u „todт

P _ k u „ ( t ) - A f e ^{-в (} ‘-"u o ( T ) d т + Pt _ ( k + KtT ) u „ ( t ) - A _                0                          _l                               _

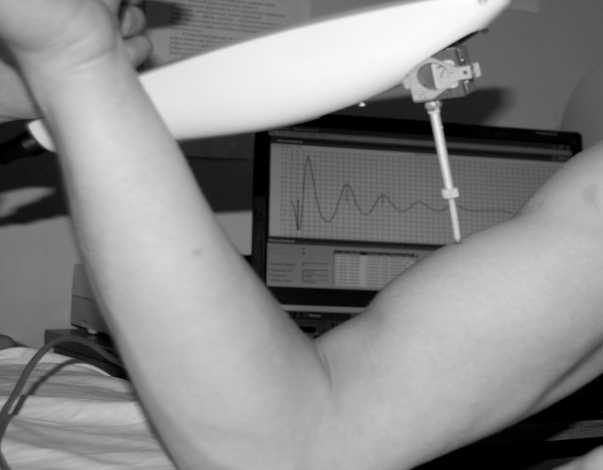
Рис. 4. Процедура миометрии двуглавой мышцы плеча

Если для характеризации напряженной мышцы использовать те же вязкоупругие характеристики E , A и р , что и для пассивной, то последнее уравнение можно переписать в виде:

P = 0,851 п RE a

u ₀( t ) - A a j e -^{pa (} t ^-T ) u ₀( t ) d т

Здесь E ^а, A ^а, р ^а - вязкоупругие характеристики мышцы в активном (напряженном) состоянии. Сопоставив выражения (19), (18) и (5), можно установить взаимосвязь между характеристиками пассивной мышцы ( E ^а, A ^а, р ^а), свойствами мышцы в напряженном состоянии ( E ^п, A ^п, р ^п) и силой T , генерируемой мышцей,

E ^а = E ^п + T—KT —, 0,851 п R

аа

A-E- = 1,   р ^а =р ^п.

A ^п E ^п

Анализ результатов

Тестирование спортсменов в части биомеханической диагностики двуглавой мышцы плеча ( m. biceps brachii ) (рис. 4) позволило определить вязкоупругие характеристики последней в пассивном (расслабленном) и активном (напряженном) состояниях. Используя для каждого измерения разработанный метод определения вязкоупругих свойств (12), (14), (17), оценивали характеристики мышцы в расслабленном и напряженном состояниях. Анализировались только те данные, которые имели «норму реакции» для данной скелетной мышцы, отражающие положительную способность генерировать, рекуперировать и рассеивать механическую энергию в ходе динамических движений (табл. 1).

Результаты расчетов представлены в таблице 2, где даны также значения абсолютной и относительной погрешностей вязкоупругих характеристик. Можно отметить приемлемую точность определения механических характеристик (относительная погрешность не превышает 5%). Найденный по предложенному методу

Таблица 1

Параметры двухглавой мышцы плеча, диагностируемые прибором «Миометр UT 98-01»

№ измере ния	Расслабленное состояние				Напряженное состояние
	F , Гц	D	H , Н/м	t 1 , мс	F , Гц	D	H , Н/м	t 1 , мс
1	10,20	1,65	95,36	15,38	15,15	0,55	183,04	12,50
2	8,81	2,90	84,63	17,39	16,02	0,79	206,52	12,05
3	8,20	2,99	95,98	17,25	16,67	0,71	220,51	11,94
4	10,64	1,61	101,82	15,46	16,67	0,61	221,16	11,89
5	10,64	1,61	101,82	15,46	16,89	0,62	226,57	12,90

Таблица 2

Расчетные вязкоупругие характеристики материала мышцы

Состояние E, кПа A, с-1 β-1 Расслабленное 45,9 ± 1,4 (3,1 %) 112,87 ± 5,151 (4,6 %) 193,953 ± 1,992 (1 %) Напряженное 71,7 ± 2,5 (3,5 %) 68,186 ± 2,906 (4,3 %) 199,33 ± 4,406 (2,2 %) модуль Юнга материала мышцы в пассивном состоянии (Eп = 45,9 кПа) оказался несколько ниже значения 100 кПа для мышечной ткани по литературным данным [1], что можно объяснить наложением изгибных перемещений мышцы при индентировании.

Из таблицы 2 следует, что диапазоны изменения величин β ^а и β ^п пересекаются. A ^а E ^а

Вводя безразмерную величину Ω = и используя вязкоупругие характеристики, AпEп представленные в таблице 2, получим Ω = 0,944 ± 0,146. Можно утверждать, что полученные результаты подтверждают справедливость второго и третьего равенств системы (20).

Заключение

Показана возможность быстрого и неинвазивного определения вязкоупругих параметров мышечной ткани (модуля Юнга и параметров ядра релаксации), необходимых для объективной характеризации состояния скелетных мышц и оптимизации тренировочных режимов спортсменов. Установлено, что изменение механических характеристик мышцы при активации сократительной функции определяется величиной генерируемой силы натяжения.