Метод определения тензора инерции на программных движениях

Элементы тензора инерции и моменты инерции. Тензор инерции в точке О твердого тела в связанной с телом системе Oxyz задают матрицей осевых и центробежных моментов инерции вида

J =

I x I yx I zx

I xy I y I zy

I yz I z

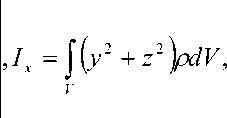
1 = Iyx = -j PxydV

V

Момент инерции тела относительно оси, заданной ортом e _i , вектор-строкой e i =[ e ix e iy e iz ], представляется в виде произведения век-тор-строки U =[ I x I y I z I xy I yz I xz ] и вектор-столбца A i , составленного из квадратов и двойных произведений направляющих

222              ²

i i , i ix iy iz ix iy iy iz ix iz , i = 1,...,6

Рассмотрим виртуальный конус с осью Oz, углом (2α) при вершине O, на конусе равномерно распределим пять осей с ортами e1,..., e5, орт e6 направим вдоль оси Oz, орт e1 расположим в плоскости Oxz, а последующие орты получаем последовательно поворотами на угол β=72o вокруг Oz. Получаем ei = [cos(tp - в), sin(tp - P), ctga]sina, i = 1,...,5, e6 = [0,0,1].

Посредством горизонтального объединения шести матричных равенств (2) получаем уравнение UA = I 0 , и формулу для вектор-строки U :

U = I о B ,

I о = [ 1 1 ,---, 1 6 ]

A = [ A ,---, A 6J

B = A ^{- 1} ,det B = 1/det A

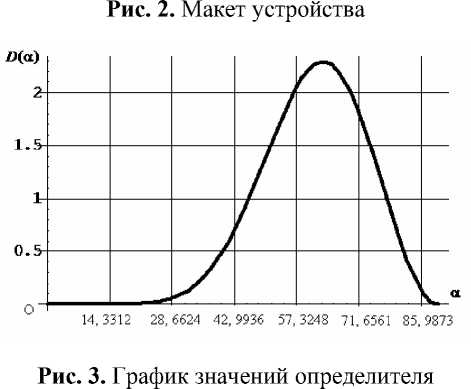
Исполнительное устройство (рис. 1, рис. 2) состоит из сервопривода 1 с робастной системой управления, платформы 2 , шагового двигателя 3 , подъемника 4 , шарнира 5 , платформы 6 с закрепленным на ней изделием 7 . По условиям эксплуатации желательно, чтобы угол α был небольшим, но с другой стороны при малом α имеем малое значение определителя D ( α )=det A , т.е. – плохо обусловленную задачу [11]. На рис. 3 показан график значений определителя, представленного функцией D ( α )=27,95 sin⁸ α cos² α , максимальное значение D max ≈2,29 достигается в случае направления ортов по осям икосаэдра, при угле α 0 ≈63,43^o. Будем считать систему достаточно хорошо обусловленной при выполнении условия: | D ( α )|≥0,5, т.е. при значении угла из интервала a e [40 0 ; 82] (рис. 3).

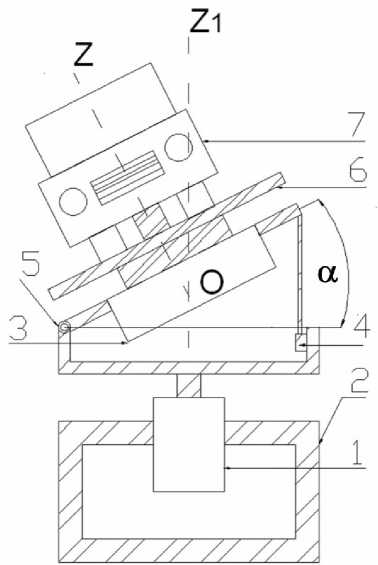
Рис. 1. Схема устройства

Расчетная формула для моментов инерции. Осевой момент инерции твердого тела будем определять на следующих реверсивных тормозных-разгонных вращениях, состоящих из замедленного вращения на угловом интервале [v0V1 = V0 + д], д > о с повторением в обратном порядке вращения на интервале [V1,V0]. Торможение может быть неуправляемым, но замеряемым, допускается замеряемый выбег за пределы интервала до некоторого значения Vr = v(tr). Затем осуществляем обратное движение, рассчитанное по замеренному движению. Пусть методом точечной аппроксимации получено уравнение торможения V = f (t) при t e [10, tr ], тогда уравнение обратного движения есть v = f (t') при t' = 10 + tr -1. Работа сил тяжести равна нулю ввиду вертикальности оси вращения, поэтому программные движения можно выполнять в любом ограниченном угловом интервале. По теореме кинетической энергии на тормозном и обратном вращении имеем уравнения

(Iо + IX«12 - «o ) = 2(A + V),

(Iо +1« - « )= 2(A ‘ + V')      (4)

« 1 = V & ( ¹ 1 ), to o = 4 ^{( 1} o )

Здесь A , A ' – работы крутящего момента на интервале [ у 0 , ^ 1 ] ; V , V ' - работы диссипативных сил, I – момент инерции изделия, I 0 – приведенный момент инерции исполнительного устройства. Вычитая почленно уравнения (4), получаем расчетную формулу, определяющую осевой момент инерции тела через разность работ крутящего момента

- 1

• 1    = (A '- A)(« - «4 ) - Io

.     (5)

Формула (5) не содержит работы диссипативных сил и может быть использована на динамически симметричных устройствах с существенным трением и аэродинамическим сопротивлением, удовлетворяющих условию равенства их работ на тормозном и обратном движении, что можно обеспечить симметричной оболочкой на изделии.

В конце первого эксперимента включается электродвигатель собственного вращения для поворота на угол ∆φ=72⁰ и установки изделия в новом угловом положении по отношению к оси Oz 1 . Выполняется 5 испытаний. Шестое испытание выполняем при установке α =0 (рис. 1), где в расчетах следует применить формулу Гюйгенса-Штейнера. Итак, по формуле типа (5) находим 6 осевых моментов инерций изделия I 1 ,…, I 6 , при этом осевые моменты инерции устройства I 01 ,…, I 06 находят заранее на отдельных испытаниях устройства без нагрузки.

Допустим, что замеряется потребление двигателем электроэнергии E и E ' на рассматриваемых угловых интервалах. Она расходуется на механические работы A + V и A ' + V ' , а также - на омические потери и на изменение электромагнитного поля

E = A + V + 3,

E ' = A Ч V ' + 3 ,

A '- A = E '- E - ( 3'-3 ), 3> 3

Подставляя последнее равенство в (5), получим энергетическую формулу

I = (E - E'+ 3 - 3)(«2 - «12)-1 -1o, (6)

выражающую момент инерции тела относительно каждой оси через разность потребляемой электроэнергии и разность омических потерь в контурах. Потери 3’ , 3 можно оценить на испытании с эталонным телом.

Пусть угол φ не фиксирован, медленно изменяется, обеспечивая непрерывное изменение положения в теле оси Oz 1 . Тогда имеем угловую скорость сферического движения в виде « = у к 1 + ф к к ф к 1 , и с малой погрешностью можно применить формулы типа (5) на интервалах времени [ 1 , -, t i _{+ 1}], i = 1,...,5 , на которых φ получает изменение 72⁰.

Работа выполнена при финансовой поддержке гранта РФФИ 06-08-01338-а и гранта Комитета по науке и высшей школе Санкт-Петербурга за 2009г.