Метод оптимизации геометрии зеркальных антенн с диаграммой направленности специального вида

Введение1

Зеркальные антенны с диаграммами направленности (ДН) специального вида широко используются при построении радиолокационных и радионавигационных комплексов, радиотехнических систем дистанционного зондирования и картографирования [1]. Для систем связи особое значение имеют зеркальные антенны со сверхнизким (до –60 дБ) уровнем боковых лепестков ДН. Формирование таких ДН с помощью зеркальных антенн имеет ряд преимуществ в сравнении с фазированными антенными решетками, прежде всего вследствие компактности и простоты конструкции зеркальных антенн, состоящих из рефлектора специальной формы и облучателя. ДН специального вида в радиолокационных и радионавигационных комплексах должны обеспечивать равномерность мощности излучения в пределах заданной угловой области. В этом случае цели, характеризуемые одинаковыми рассеивающими свойствами (например, радиолокационным сечением рассеяния), в одинаковой степени воспринимаются в границах зоны перекрытия, обеспечивая высокую эффективность обработки радиолокационной информации. Примером ДН специального вида может служить косекансная ДН, которая используется как для наземных, так и для бортовых комплексов.2

Для синтеза поверхности рефлектора зеркальной антенны с ДН специального вида наиболее часто используются методы геометрической оптики (ГО) [1, 2], следовательно, результаты синтеза тем точнее, чем больше размеры и радиус кривизны рефлектора по сравнению с длиной волны λ . Вместе с тем, методы ГО принципиально не могут быть использованы для анализа дифракционных явлений, возникающих на кромках рефлектора и существенно искажающих ДН. Кроме того, эти методы неприменимы для оптимизации поверхности рефлектора в заданном частотном диапазоне. Следовательно, методы ГО являются приближенными методами синтеза, и в основном используются для нахождения профиля сечения цилиндри-

ческого рефлектора. При этом для расчета ДН в вертикальной плоскости используется апертурный метод, не учитывающий строгую картину фазовых распределений в апертуре антенны. Поэтому на практике полученные результаты часто приходится корректировать, но простота и ясность физических концепций, лежащих в основе методов ГО, определила их широкое применение в инженерной практике проектирования зеркальных антенн.

Методы расчёта профиля зеркальной

антенны двойной кривизны с заданной ДН

Рассмотрим методы оптимизации геометрических характеристик рефлектора зеркальной антенны двойной кривизны для формирования косе-кансной ДН в вертикальной плоскости. В приближении ГО обычно определяют профиль сечения цилиндрического рефлектора, профиль рефлектора в горизонтальной плоскости выбирают параболическим, исходя из заданных требований к ДН в горизонтальной плоскости. Основные геометрические характеристики профиля центрального сечения рефлектора в вертикальной плоскости и лучи в апертуре антенны изображены на рис. 1.

для решения которого необходимо знание функции 6 ( y ) . Необходимо отметить, что решение нелинейных интегральных уравнений затруднено вследствие существования неопределенных точек ветвления, поэтому решение (2) обычно проводят методом последовательных приближений [3].

В другом методе функцию 6 ( y ) находят как решение нелинейного дифференциального уравнения второго порядка [2]:

d ² 6 „ 1 dP ( 6 ) f d of

+ 2—II - dy2   P(6) dy vdV /

—

1 dG (y) G (6) dy

= 0,

Для кривой сечения, которая предполагается дифференцируемой, из рис. 1 следует дифферен-

где P ( 6 ) - заданная косекансная ДН по мощности; G ( y ) — заданная ДН облучателя по мощности. Дифференциальное уравнение (3) можно получить из условия баланса энергии электромагнитного поля облучателя и отраженного от рефлектора электромагнитного поля в единичном телесном угле. Решить это уравнение можно методом последовательных приближений, на каждом

циальное уравнение [2]

шаге которого производится линеризация уравнения, приводящая к краевой задаче с заданными

d

—ln p = tg d y

V + 6 ( y )

где p ( v ) — расстояние в сечении профиля от точки расположения облучателя до точки отражения на кривой; 6 - угол, образуемый падающим лучом с горизонтальной плоскостью; y — угол, образуемый отраженным лучом с горизонтальной плоскостью. Уравнение (1) путем интегрирования в заданном угловом секторе можно преобразовать в нелинейное интегральное уравнение

граничными условиями.

После определения функции 6 ( y ) уравнение профиля центрального сечения рефлектора можно

записать в следующем виде:

'^V 2

P⁽Y ) = P⁽Y i ) exP J J tg

₄ Vi ^l

y+Q^y)

d Yf ,

где расстояние p ( v , ) определяется из условия допустимого уровня ДН облучателя в секторе уг-

ln -^Jtg ' • d Y , P⁽V i ) V , L ² J

лов y ₂ — V i .

Решение дифференциального уравнения (1) можно упростить, используя основные закономерности метода геометрической оптики. Вводя условие баланса энергии электромагнитного поля в

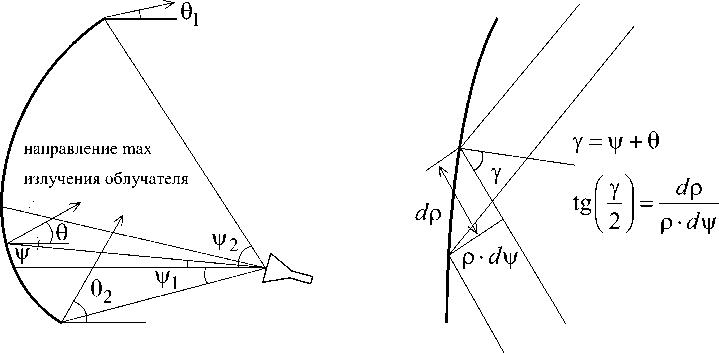
Рис. 1. Геометрия задачи

единичных телесных углах для падающего поля облучателя и отраженного поля от рефлектора, получим калибровочное соотношение равенства полной мощности излучения, падающей на рефлектор, и мощности излучения:

V

V 2

J G ( v ) d V' J G ( v ) d V

-1

V 1

_ V 1

= J P ( 0 ) d O'

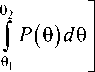
С учетом этого условия решение дифференциального уравнения (1) для косекансной ДН принимает следующий вид [2]:

ctg 9 = ctg 9 1 + ( ctg 0 2 - ctg 9 1 ) x

-1

VV xj G(v)dV' J G(v)dV .

• V1               Lvi_

Следует отметить, что рассмотренные методы являются приближенными, поэтому практическая реализация расчетного профиля рефлектора может потребовать определенной коррекции, особенно для рефлекторов относительно небольших размеров, при этом внутри допустимой области изменения размеров рефлектора существует оптимальное расстояние до облучателя. Угловой сектор v ₂ —V 1 обычно выбирают с учетом требования небольших уровней мощности первичного поля облучателя за пределами рефлектора (ослабление плотности потока мощности на 10 дБ) и равномерности ДН облучателя в апертуре антенны. Изменяя в небольших пределах расчетный профиль рефлектора, можно получить приемлемый уровень искажений ДН антенны.

Общим недостатком рассмотренных методов является раздельное определение функции 9 ( v ) и уравнения профиля рефлектора. При этом применяемые численные методы имеют разные уровни точности, что приводит дополнительным погрешностям синтеза ДН антенны. В приближенных методах особую важность имеют численные методы с контролем точности промежуточных вычислений для введенной математической модели антенны, когда синтез геометрии профиля рефлектора и синтез ДН антенны производится одновременно на каждом шаге последовательных приближений с заданной точностью.

Метод последовательных приближений для синтеза профиля рефлектора

Рассмотрим развитие метода последовательных приближений для решения нелинейного интегрального уравнения (2). Введем модифицированное уравнение баланса полной мощности излучения, падающей на рефлектор, и мощности излучения [2]:

V

J

^{G (}V ) P⁽V )

7 ^{d V}' J

_ V 1

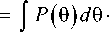
G (v)^

^d V P⁽V )

-

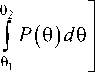
Это уравнение учитывает реальную картину распределения плотности потока мощности поля облучателя, отвечающую условию излучения [2]. В дальнейших вычислениях будем использовать квадратурные формулы Гаусса, число узлов в которых будем определять из заданной точности синтеза. Выбор этих формул обусловлен требованием контроля точности и простотой программной реализации. Структура программного комплекса для синтеза заданной ДН выглядит следующим образом.

• 1.    Введем номер шага n = 1 и начальное приближение уравнения профиля рефлектора в виде параболической функции

• 2.    Из соотношения (7) находим функцию 9 ( v )

• 3.    Присваиваем номер шага n = n + 1, из выражения (4) находим уравнение профиля р _{n + 1} ( v ) •

• 4.    Находим норму разности § = |р _{n + 1} -р n |, например, в виде чебышевского критерия.

• 5.    Если величина § меньше заданной точности синтеза, то программа завершает работу; иначе Р n = Р n _{+ 1} и переходим к пункту 2.

, х 1 + cos V

Р n ( v )= "---------- .                              ⁽⁸⁾

1 + cos V 1

с использованием подпрограмм нахождения корней нелинейных уравнений и квадратурных формул Гаусса с числом узлов N = 28. Вычислительные эксперименты показывают, что относительная погрешность вычислений этого этапа имеет порядок 10^–9 . Вычисления производятся в цикле для углового сектора v ₂ -V 1 с заданным дискретом Av , для каждого угла V решается нелинейное уравнение (7) для нахождения соответствующего значения 9 .

Отметим, что вычисления с повышенной точностью обеспечивают меньшее количество шагов метода последовательных приближений в сравнении с менее точными расчетными соотношениями. Для рефлекторов относительно небольших размеров количество итераций не превышает 10.

Расчет ДН антенны апертурным методом производится по следующему выражению:

V2 ______

F ( 9 ) = J V G (v) exp { z^ p(v)[ 1 + cos (v + 9)_ } d V , (9)

V 1

где k = 2л/Х , следовательно, частотные свойства антенны зависят как от поля излучения облучателя, так и от расчетного профиля рефлектора. Для оптимизации ДН антенны в заданном частотном диапазоне синтез профиля рефлектора необходимо проводить на нескольких фиксированных частотах, одновременно контролируя ДН антенны. С помощью среднеквадратичного критерия можно определить оптимальный вариант профиля, если такой выбор затруднен, то производится коррекция профиля. Эта коррекция заключается в процедуре сегментации профиля, так как в большинстве случаев удается выделить общую, слабо меняющуюся в диапазоне частот параболическую часть рефлектора. Варьируя сегментами, соответствующих оптимальным ДН для фиксированных частот, в большинстве случаев удается получить синтезированный профиль, для которого ДН антенны наиболее полно соответствует заданным требованиям. Кроме того, существует еще одна характерная особенность рассматриваемой задачи – возмож- ность выбора расположения облучателя, так как в отличие от зеркальных параболических антенн с фиксированным расположением облучателя в точке фокуса для косекансной ДН можно варьировать координаты облучателя в вертикальной плоскости для оптимизации ДН антенны в полосе частот.

Примеры синтеза ДН и профиля рефлектора

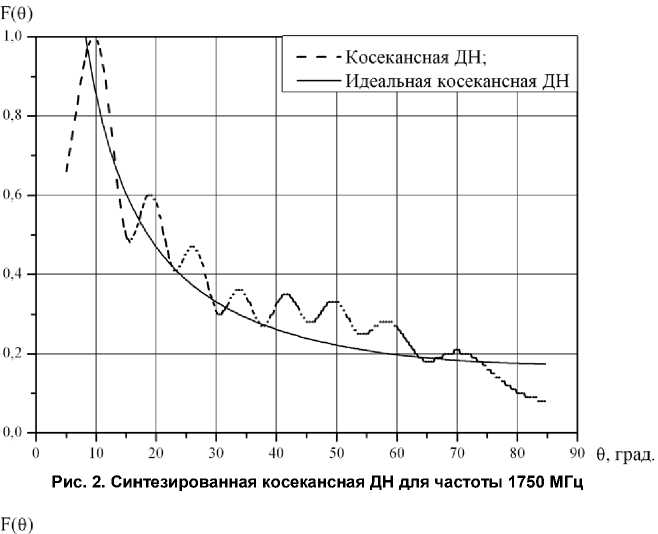
В качестве примера рассмотрим следующую задачу: синтезировать профиль центрального сечения цилиндрического рефлектора для получения косекансной ДН в угловом секторе 7–85°; частотный диапазон 1750–2250 МГц; облучатель – рупорный с горизонтальной поляризацией; ширина ДН в горизонтальной плоскости – 3°.

Примеры синтезированных ДН приведены на рис. 2–4.

0.0--1--1--1--1--1--1-----------1-----------1--1-----------।-----------1----------

0       10      20      30      40      50      60      70 SO 90 9, град.

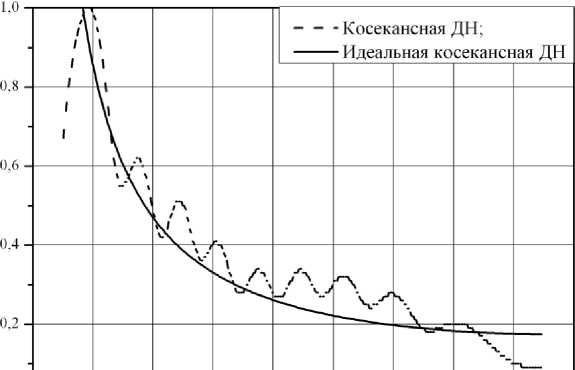
Рис. 3. Синтезированная косекансная ДН для частоты 2000 МГц

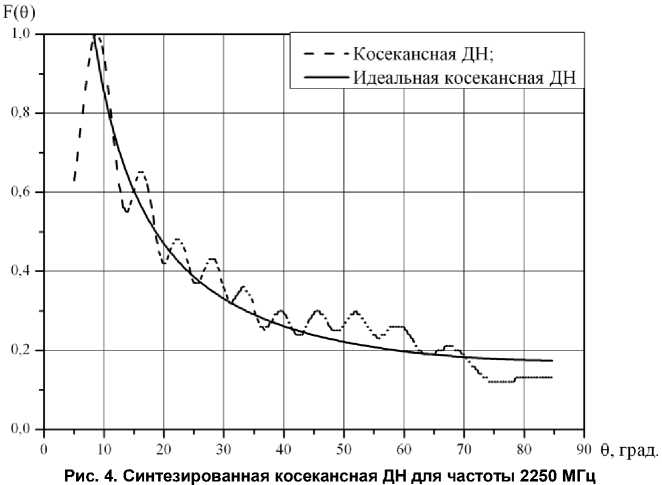
И з эти х гра ф иков сл е д у е т, что в в е р х ней части час тот ного д и ап аз она в Д Н а нтенны появл яются доп о л н ител ь н ы е ос ц илляц ии, а мплит у да кот ор ых отн оси те л ь но н ев ел и ка и в це л ом Д Н бол ьше соотв е тс тву е т з а данным тр е бов а н иям . Э то м ож но объяснить быс трым из м е не н ие м прив еде н ного ф ок ус ного ра с с тоя ния для в е рх н и х ча с тот, что в св ою оче ре дь прив оди т к дополни т ел ь ным фа з ов ы м ис каж е н иям в апе рт уре а нтенны. Наибол ь шие о т кл онен ия в ДН наблюд а ютс я в ин те рв а л е у гл ов 10–20° , ос обе нн о н а н ижн и х ча с тотах диапа зона. Дл я з а дан ного набора исх од ных данн ых ц ел е с оо бр а з но с инт ез профи л я прои з в е с ти на ни ж ней ча стоте д иа па з о на . Е с ли эт и о ткл о не н ия пре в ышают за да н ные , то не обх о д им о произ в е ст и корре кц ию профил я по пре д л ож е н ной м е тодике .

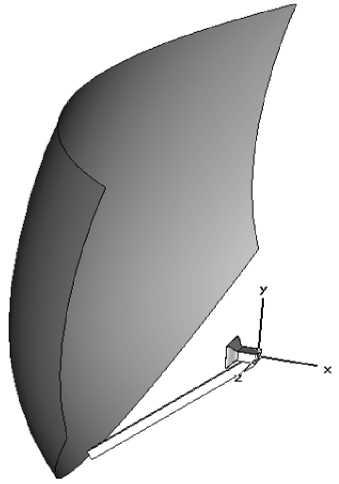
Рис. 5. Синтезированный рефлектор двойной кривизны

На рис. 5 приведена форма синтезированного рефлектора двойной кривизны для формирования ДН с заданными свойствами в полосе частот.

Практическая реализация проектируемой антенны требует выполнения определенного допуска на точность соответствия геометрии рефлектора и синтезированного профиля. В соответствии с [2] этот допуск определяется следующим образом:

А = ±

8 ( 1 + cos v )

Следовательно, наибольшую точность соответствия поверхности рефлектора антенны необходимо обеспечивать для центральной части, на краях рефлектора требования к точности могут быть несколько снижены, что упрощает практическую реализацию антенны.

Необходимо отметить, что, оставаясь в рамках апертурного метода и основных положений метода ГО, принципиально невозможно определить искажения ДН антенны, вызванные дифракционными явлениями на кромках рефлектора. Строгие электродинамические методы для рассматриваемой задачи приводят к интегральным уравнениям для распределений токов на поверхности рефлектора. Для рефлекторов больших электрических размеров эти уравнения приводят к необходимости решения систем линейных алгебраических уравнений очень большой размерности, требующих вычислительных ресурсов суперкомпьютеров. Вместе с тем, как показано в статье [4], для решения поставленной задачи строгими элек- тродинамическими методами, учитывающими реальные фазовые распределения в апертуре антенны и векторный характер задачи, можно воспользоваться результатами решения более простой двумерной скалярной задачи для E-поляризации. При этом ДН в вертикальной плоскости будут совпадать.

Выводы

• 1.    Предложенный метод синтеза профиля рефлектора двойной кривизны позволяет производить контроль точности вычислений и соответствия ДН в вертикальной плоскости на каждом шаге последовательных приближений.

• 2.    Использование вычислительных процедур повышенной точности ускоряет сходимость предложенного метода последовательных приближений.

• 3.    Синтез профиля рефлектора и ДН в полосе частот требует предварительных расчетов на сетке фиксированных частот. Сегментация профиля рефлектора и компоновка его из различных участков профилей для разных частот позволяет выбрать наиболее приемлемый вариант для выбранного критерия соответствия.

• 4.    Более точные методы синтеза должны основываться на строгих электродинамических

принципах, так как они позволяют учитывать дифракционные явления, которые для рефлекторов относительно небольших размеров приводят к существенным искажениям ДН.