Метод параллельного симплектического интегрирования уравнений движения малых тел солнечной системы

В статье предложен новый метод параллельного симплектического интегрирования уравнений движения для малых тел Солнечной системы, позволяющий использовать для решения небесно-механических задач кластеры и суперкомпьютеры.

Задачи, связанные с решением задачи N тел, - это сложные математические задачи, требующие применения эффективных численных методов и огромных компьютерных мощностей. Начиная со статьи Висдома и Холмана [4], симплектические методы стали популярным инструментом решения таких задач. Симплектические интеграторы являются наиболее быстрыми среди интеграторов N тел, а также имеют достаточно большую точность, что делает их подходящими для широкого спектра проблем динамической астрономии. Для наиболее эффективного исполь зования симплектических интеграторов в статье предложен метод распараллеливания интегрирования, позволяющий производить вычисления на кластерах и суперкомпьютерах.

Симплектическое интегрирование проводится отдельно для планет и отдельно для частиц.

Запишем гамильтониан для системы N тел в инерциальной системе отсчета

N н^,Рд=^ /=о

-2    N-\ N

1=0 j=M

т^ \qi-qjV

(i)

где q_t — обобщенные координаты, р₁ - обобщенные импульсы, m_t - масса /-го тела, / = 0 соответствует Солнцу. Для планет будем использовать координаты Якоби. Обозначим координаты !

Якоби штрихом, первая координата Якоби х0 - центр масс. Тогда где Xj определяет местоположение центра масс / тел j=o

Тогда (1) перепишем в виде

Я = Якер1-Я1п1ег,                                   (4)

где п-1 ^kepl=Z /=1

Г -'2 п А А__ Gm^ ?^mi ⁷i ,

п-1

Winter =2 ^-'"О i=l

Г1     1        "

™ - I

^^ ^оУ 0

Gm^j

Интегрирование планет происходит с постоянным шагом по времени по схеме интегратора второго порядка 52(т), и для каждой частицы проводится дополнительное вычисление координат планет (Чегодаева [3]).Для решения задач связанных с кометами, астероидами и другими малыми телами Солнечной системы более удобен интегратор с переменным временным шагом Емельяненко [1].

Чегодаева Е.А. Метод параллельного симплектического интегрирования уравнений движения малых тел Солнечной системы

Саха, Стадель и Тремэйн [2] показали, что параллельный алгоритм основанный на распараллеливании уравнений движении дает очень небольшую выгоду из-за больших затрат на обмене данными между потоками. Поэтому в данном методе использовалась простая, но эффективная схема, представленная на рисунке. Поскольку вычисления проводятся отдельно для планет и отдельно для частиц, то удобно разделить программу на ^+l процессов (потоков). Нулевой процесс занят расчетом планет и рассыпкой данных между остальными N процессами, которые заняты более затратными вычислениями уравнений движения частиц. Такая схема распараллеливания наиболее эффективна.

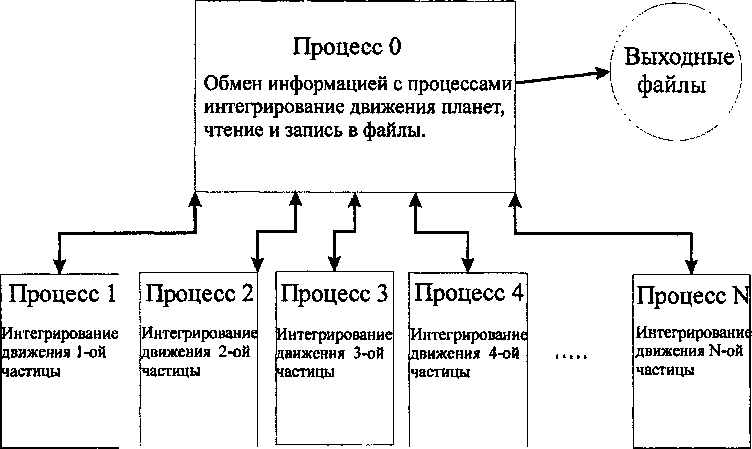
Схема занятости процессов

Заключение. На основе данного метода написана программа на Fortran с использованием MPI. Проведено тестирование на 52-х процессорном суперкомпьютере ЮУрГУ «Infinity». Данный метод позволит решать множество задач небесной механики и динамической астрономии.

Данная работа была поддержана грантами РФФИ 04-02-96042 и при финансовой поддержке Правительства Челябинской области.