Метод поиска неподвижных точек в задаче улучшения управляющих параметров

1.    Метод нелокального улучшения

Рассматривается линейная по управлению задача:

Φ ( u ) = ϕ ( x ( t ₁ )) + ∫ _T ( ( a ( x ( t ), t ), u } + d ( x ( t ), t )) dt → m _∈ in ,               (1)

x ɺ ( t ) = A ( x ( t ), t ) u + b ( x ( t ), t ) , x ( t ₀) = x ⁰ , u ∈ U , t ∈ T ,                 (2)

где матричная функция A(x, t) , векторные функции a(x, t) , b(x,t) , функции ϕ(x) , d(x, t) являются квадратичными по x и непрерывными по t на множестве Rn × T . Множество U ⊂ Rm выпукло и компактно.

Функция Понтрягина и стандартная сопряженная система имеют вид:

H(ψ,x,u,t) = H0(ψ,x,t) + ( H1(ψ,x,t),u } ,

H ₀( ψ , x , t ) =< ψ , b ( x , t ) ) - d ( x , t ) , H ₁( ψ , x , t ) = A^T ( x , t ) ψ - a ( x , t )

ψɺ (t) = -Hx(ψ(t), x(t), w, t) ,    t∈ T(4)

Введем модифицированную сопряженную систему:

pɺ(t) = -Hx(p(t), x(t), w, t) - 12Hxx(p(t), x(t), w, t)z(t)(5)

Для допустимых управлений u , v обозначим ∆ _v Φ ( u ) – приращение целевой функции; x ( t , v ) , t ∈ T – решение системы (2) при u = v , x ( t ₀, v ) = x ⁰ ; ψ ( t , v ), t ∈ T – решение системы (4) при w = v , x = x ( t , v ) , ψ ( t ₁, v ) = - ϕ _x ( x ( t ₁, v )) ; p ( t , u , v ) , t ∈ T – решение системы (5) при w = u , x ( t ) = x ( t , u ) , z = x ( t , v ) - x ( t , u ) с краевым условием

p(t1,u,v) = -ϕx(x(t1,u)) - 12ϕxx(x(t1,u))y(6)

где частные производные по x вычисляются при y = x ( t ₁ , v ) - x ( t ₁ , u ).

Поставим задачу об улучшении управления u ⁰ ∈ U : найти управление v ∈ U с условием ∆ _v Φ ( u ⁰ ) ≤ 0.

Точная формула приращения целевой функции в рассматриваемой задаче принимает вид [1]:

• ∆vΦ(u) = - ∫ H1(p(t, u, v), x(t, v), t)dt, v - u ,(7)

v _T

Для заданного α >  0 введем отображение W ^α по формуле

W α(u, v) = PU(u +α∫ H1(p(t,u,v), x(t,v),t)dt), u∈U,v∈ U ,(8)

Необходимое условие оптимальности для управления u е U с помощью отображения (8) представляется в виде и = Wа(u, и), а > 0.                             (9)

Формула (7) позволяет построить метод нелокального улучшения с помощью операции проектирования (8).

Первый проекционный метод нелокального улучшения: для заданных а > 0 и и0 е U сформируем отображение W— (v) = Wа (и0, v), v е U и найдем решение уравнения v = W— (v).                                (10)

Показано [1], что решение va е U системы (10) обеспечивает улучшение. В силу известного свойства проекции имеем j^ H 1( p (t, и °, va), x (t, va), t) dt, va - и°^ > — ||v“ - и 0|| .

Отсюда из формулы (7) следует уменьшение целевой функции с оценкой

Ф ( v ^— ) -Ф ( и °) <- -| | v “ - и ⁰||².                        (11)

Таким образом, первый проекционный метод нелокального улучшения заключаются в нахождении неподвижной точки v ^— е U отображения W — . В силу оценки (11) строгое улучшение гарантируется (в том числе и для управления и ⁰ е U , удовлетворяющего необходимому условию (9)), если v ^— Ф и ⁰ .

• 2.    Численные эксперименты

В качестве иллюстрации работы метода рассмотрим следующий пример:

1 2

^ min,

Ф ( и ) = —j x ²( t ) dt

x ( t ) = и , x (0) = 1, и е U = [ - 1,1],   t е T = [0,2]

и ⁰ = 0

Данный пример допускает аналитическое решение.

Функция Понтрягина и модифицированная сопряженная система принимают вид:

„        1 2

H = ри - — x

p ( t ) = x ( t ) + 2 y ( t ), p (2) = 0 .

Фазовая траектория, соответствующая управлению и ⁰ : x ( t , и ⁰ ) = 1, t е T . Значение функционала для начального управления: Ф ( и ⁰ ) = 1 .

Решение x ( t , v ) фазовой системы, соответствующее управлению v :

x ( t , v ) = vt + 1, t е T .

Решение p ( t , и °, v ) модифицированной сопряженной системы:

2 vt p (t, и , v) =--+1 - (2 + v)

Сформируем отображение W — ( v ) = W ^а ( и °, v ):

W 1 ^— ( v ) = P U ( и ⁰ + а[ H 1 ( p ( t , и °, v ), x ( t , v ), t ) dt ) = P U (— v - 2) =

T                                    ³

- 1, - ⁴ v - 2 <- 1 3

4   .

— v - 2, 3

—v 3

2 < 1 = <|

—v - 2, v е [-1;),

1, - ⁴ v - 2 >  1

3 - 1, v е [ - — ;1]

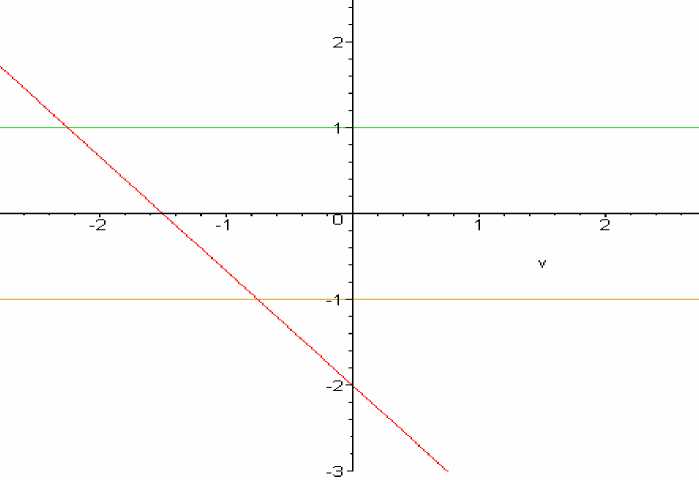
Таким образом, задача о неподвижной точке имеет вид:

v = P u ( - 3 v - 2)                            (12)

Уравнение допускает аналитическое решение v = - ⁶ ^ 0,857142857.

при т * 0:

Численные расчеты применялись для исходного (12) и эквивалентного уравнения v = v + т( v - Pu (- з v - 2))                       (13)

Для решения обоих уравнений применялся метод простой итерации [2].

В ходе численных экспериментов установлено, что итерационный процесс для решения исходного уравнения (12) методом простой итерации сходится при значениях ^а <  1. При стандартном значении ^а = ¹ процесс не сходится по начальному приближению даже в минимально возможной машинной окрестности точного решения, при этом процесс итераций зацикливается с повторением значений -1 и -2/3. При уменьшении ^а до 0,7 наблюдается аналогичный тип расходимости. При дальнейшем уменьшении, начиная со значения ^а = 0,7, итерационный процесс сходится, причем наилучшая сходимость получена при значениях в промежутке [0,01; 0,1]. Область сходимости по начальному приближению включает допустимое множество U = ^{[ - 1;1]}. При уменьшении параметра ^а вплоть до значений, сравнимых с машинным нулем, сходимость процесса итераций замедляется, и область сходимости по-прежнему включает все множество допустимых значений. Далее из-за ошибок округления он перестает сходиться и останавливается.

При увеличении ^а > ¹ процесс сходится, получаем точку ^v = ^{- 1}.

Для модифицированного уравнения (13) при стандартном значении проекционного параметра ^а = ¹ варьировался параметр ^т . При ^т >  ⁰ и его дальнейшем увеличении итерационный процесс расходится, наблюдается неограниченный рост последовательности приближений до ⁺” . При отрицательных значениях получаем сходимость на всей области допустимых значений управления, причем наилучшую по количеству итераций в диапазоне от -0,1 до -0,9. При уменьшении ^т , начиная с -1, процесс итераций расходится, последовательность приближений неограниченно убывает до ^-” .

Заключение

Численные расчеты продемонстрировали вычислительную эффективность предлагаемых алгоритмов решения задач о неподвижной точке. Показана возможность расширения области сходимости итерационных методов вплоть до всей области значений управляющих параметров только за счет варьирования проекционного параметра а. Также продемонстрирована возможность расширения области сходимости за счет преобразования к эквивалентной задаче о неподвижной точке по параметру сходимости τ при фиксированном значении проекционного параметра.