Метод поиска особых точек дактилоскопических изображений с использованием поля направлений

Персональная идентификация с помощью распознавания дактилограмм вызывает устойчивый интерес и важна для задач обеспечения безопасности. В настоящее время, большинство систем для распознавания дактилограмм, используют или анализ структуры полос дактилограммы (папиллярного узора) с помощью оптической нейронной сети, предназначенной для выделения участков прямых линий на изображении [1], или подсчитывают число Галтона (число разветвлений и концов полос дактилограммы) [2]. Все эти методы являются операциями с определенными затратами машинного времени. Причем наибольшее время тратится на процесс сравнения набора признаков дактилограммы, с имеющимися в базе данных. В работах [3,4] исследуется метод распознавания дактилограмм по полю направлений. Т.к. вектор признаков представляет собой совокупность коэффициентов разложения по базису Адамара, процедура сравнения с базой данных была сравнительно быстрая. Но этот метод как показано в работе [5] пригоден только для баз данных небольшого размера (не более 104 элементов). Для того чтобы использовать метод поля направлений для распознавания дактилограмм в базах данных большего размера (до 106 элементов) необходимо для расширения набора признаков определять глобальные особые точки дактилограммы.

Необходимо найти положение особых точек на отфильтрованном поле направлений и определить их тип. В данной работе предлагается оригинальный метод автоматического поиска особых точек на изображениях.

Особые точки

нятно, что в точках, где дI = дI = о, в поле направ-дy дx лений возникает неопределенность 0 , т.е. направ-0

ление градиента в этих точках не определено. Эти точки называются особыми точками. Вокруг обхода таких точек поле направлений может m раз меняться в диапазоне от нуля до 2п, то есть набег фазы ^ ( x , y ) вокруг особой точки равен А ^ ( x , y ) = 2 n m , m – индекс особой точки.

В теории устойчивости решений по Ляпунову особые точки классифицируются по решениям характеристического уравнения. Так для систем двух дифференциальных уравнений первого порядка:

= P ⁽ x , y )

ly = Q(x,y)

15 t

характеристическое уравнение имеет вид:

дP дx aQ

d P

d x

a Q

= о

d x

a y

В нашем случае неопределенность отношения дy Q

— = 5- эквивалентно неопределенности отношения дx P дIdх , поэтому вместо функций Ри Q можно ис-

Функция яркости «полосатого» изображения I(x,y) имеет много локальных максимумов и минимумов и может характеризоваться своим градиентом

(d I ⁸ 1 )

v I ⁽ x , y ) = k-,T- I

(5 x дy )

вектором, который показывает направление наибольшего изменения величины яркости. Можно градиент рассматривать как комплексную функцию:

vI (x, y ) = vI (x, y) еф (y       + i II-, дx   дy

V yy )

пользовать проекции градиента функции яркости:

q = ^L p = ^L и характеристическое уравнение для дx ’     dy функции яркости изображений примет вид

д ² 1          д ² 1

д x д y         д y²

д ² 1       д ² 1

д x ²      д x д y

где

(д1/ )

p ( x , y ) = arctg

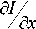
поле направлений или

функция аргумента комплексного градиента. По-

Типы особых точек

По корням характеристического уравнения S 1 и S₂ можно определить тип особой точки Седло (в криминалистике «дельта»), возникает при условии, что Im S i = 0, S 1 S ₂< 0 (рис. 1 (а). Фокус (в криминалистике «спираль»), возникает при условии, что S * = S 2 ,Re S 1 Re S ₂ > 0 (рис. 1 (б). Центр, (в криминалистике точное соответствие отсутствует, наиболее похожа «петля») (рис. 1 (в).

чего является «поле вероятностей», где вероятность есть вероятность того, что точка с данными координатами является особой. Далее из данного поля вероятностей делается заключение о том, где особые пятна (группы точек) действительно (с достаточной степенью вероятности) являются особыми точками, а затем происходит определения их типа (спираль, петля, дельта).

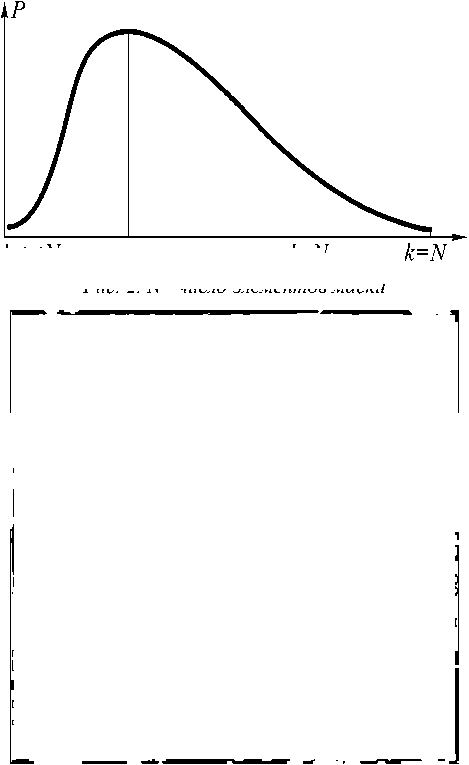
Отфильтрованное изображение поля направлений сканируется маской заданного размера. При каждом положении маски подсчитывается количество направлений, которые в нее попадают, и количества пикселей в каждом из направлений. Для положения маски определяется число, показывающее степень вероятности данной точки (в центре маски) быть особой. Это число равно произведению чисел, равных количеству пикселей данного направления. Такое определение показателя «особости» P (степени вероятности) приводит к тому, что P в особых точках достигает локального максимума. Докажем следующее утверждение:

Пусть существует числа пи i = 1,k; m? j = 1,k -1;...; Is,s = 1, 2,

k         k - 1

E n =E mj i=1          j=1

= E ls = N, причем s=1

Рис.1. Основные типы особых точек: а) седло (дельта), б) фокус (спираль), в) центр (петля)

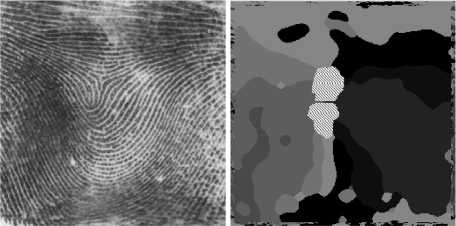
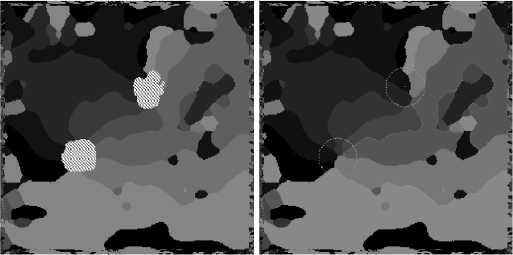
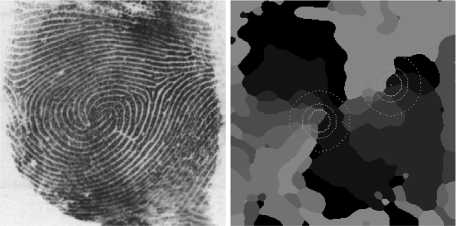
n, = n,,i * j; i, j = 1,k, m, = m,,i * j; i, j = 1,k -1,^, ijij l1 = 12; k - целое положительное число. Тогда для k<

k          k-12

P=П ⁿi >П mj >... >n ls > N.

i=1           k=1

Действительно.

Перепишем условие теоремы в следующем виде:

x к N ) k — I > k J

k-1

N-1 , k=2,3,^;

k -1

N^k (k -1)^k-1 k^k   N^k-1

(k -1)^k-1 k^k

>1,

N > 1,

k -1) k^-1

k

¹N > 1. k

Отсюда видно, что ряд

r k -1^{k 1}1

I k J k

будет

В зависимости от сочетания особых точек в дактилограмме выделяются разные типы узоров.

Метод поиска особых точек

Так как в дискретном случае операция вычисления первых и вторых производных выполняется с погрешностями для надежного поиска особых точек требуется разработка эффективных алгоритмов, адаптированных к дискретному случаю.

Рассматриваемый алгоритм основан на сканировании изображения заданной маской, результатом

стремиться к нулю при k ^ да , вследствие чего для

выполнения условия теоремы должно выполниться N ^ да. Легко показать, что при k ^ N неравенство не выполнится. Для этого подставим вместо k число N:

(N -1) N^-1

NN

N > 1,

N

N-1

N

>1, что не верно.

В данной работе под n₁, n₂,..., n_k понимается количество пикселей каждого попавшего в маску направления. Вместо равных n₁, n₂,..., n_k получаются приблизительно равные, или стремящиеся к равенству (или просто близкие) значения, поскольку на реальных сильно искаженных полях направлений абсолютного равенства чисел n₁, n₂,..., n_k достичь невозможно. При подсчете количества пикселей одного направления (цвета) подсчитывается все количество пикселей данного цвета независимо от того, в каком «пятне» они лежат, связаны ли пиксели одного цвета в одну группу или разбросаны по всей маске.

Можно доказать, что:

n ~ nj,i * j^,P = jnn                   (^

=1

будет меньше, чем когда имеет место строгое равенство:

n, = n, = n,i * j; i, j = 1, k                       (2).

ij

Пусть P = n^k и P = (n - q)(n + q)n-2,

Тогда так как n²> (n - q)(n + q)

P>P1

Изменять сомножители можно именно таким образом, чтобы сохранять их сумму

k

E n = N.

=1

Понятно, что неравенство сохраняется P>P1 при любом числе измененных сомножителей

P1 = (n - q)(n + q)(n - w)(n + w)...(n -1)(n +1) Такая формула получения P (показателя «особости» точки) будет давать тем больший результат, чем больше их попадет в маску направлений, и чем равномернее (по количеству) они в нее попадут, но до определенного предела. В таблице 1 приводятся примеры количества направлений, приблизительно поровну попавших в маску и соответствующее им число P для маски 3x3:

Как видно из таб. 1 существует максимальное количество направлений, приблизительно поровну попавших в маску (для маски 3x3 это количество равно трем), начиная с которых эта теорема перестает выполняться. Примерный вид такой зависимости показан на рис. 2:

Таблица 1.

Количество направлений	1	2	3	4	5
P	9	20	27	24	16

Как видно из рис. 2, метод корректно использовать при сочетании k, N как в левой части до вертикальной черты, где k<<N, что соответствует большим размерам маски и малому количеству направлений в поле. При масках около 7x7 и больше и количеству градаций в поле направлений 8 это хорошо выполняется.

Рис. 3. Поле направлений после ранговой фильтрации

k«N             k~N

Рис. 2. N - число элементов маски

На иллюстрации представлено отфильтрованное поле направлений. Большей по размеру рамкой обведена для примера область, внутри которой пробегает маска. Размер изображения – 256x256.

Перед этим перемножением количество каждого цвета нормируются:

norm

С = N ?,

sqw²

где c_i - новое количество, N_i - старое количество для i-ой точки; norm - количество точек, к которому сводится нормировка, sqw - количество точек в маске.

Смысл данной нормировки заключается в развязке порога, начиная с которого точка считается особой от размера маски. Если этого бы не производилось, то при изменении размера маски необходимо было бы учитывать увеличение порога, поскольку при тех же пропорциях (по количеству пикселей) вошедших в маску направлений это число будет изменяться. Кроме того, данная обработка регулирует относительные количества направлений, вошедших в маску, при которых значение «особости» будет одинаковым. Это полезно, поскольку в реальной обработке изображения идет отступление от теоремы, где сказано, что количества попавших в нее цветов должно быть одинаковым.

а                     б

Рис.4. Пример обработки поля направлений (б) пороговой обработкой. Особые пятна показаны штриховкой. Квадратами на изображении отпечатка пальца (а) отмечены положения соответствующих особых точек.

После нормировки проводится вышеупомянутая пороговая обработка, и все точки, значение «особости» P которых больше чем заданный порог считаются особыми. В результате такой обработки получаются группы особых точек – какие-то количества особых точек, находящиеся рядом. В дальнейшем будем называть такие скопления особых точек особыми пятнами.

Затем проводится преобразование особых пятен в особые точки. Для этого берется первая точка из массива особых точек, и весь массив пробегается еще раз; при этом программа смотрит, как далеко отстоит от искомой взятая из массива следующая особая точка. Если оказывается, что их расстояние Dr меньше Dosobr:

Dr = 4dx 2 + dy2 < Dosobr , где dx и dy – расстояние по горизонтали и вертикали между двумя взятыми точками, то это означает, что обе точки взяты из одного особого пятна, что фактически относится к одной настоящей особой точке. Тогда одна точка из массива особых точек удаляется. При этом алгоритм удаляет «менее особую». Однако, если параметр Dosobr подобран неверно (завышен), или же при двух очень близко расположенных особых точках, две настоящие особые точки могут после такой обработке преобразоваться в одну. На следующем примере показана такая ситуация рис.5:

а                     б

Рис. 5. Дактилограмма (а) и поле направлений с особыми пятнами (б)

В большинстве случаев так близко особые точки не располагаются, как показано на данном примере, вследствие чего величина параметра Dosobr слишком велика, чтобы интерпретировать эти две особые точки как две. После преобразования особых пятен в особые точки программа посчитает, что вследствие параметра Dosobr=60 в данном случае имеет место одна особая точка, и выберет за особую более ярко выраженную особую точку с большей величиной параметра P:

Рис. 6 Особая точка после преобразования особых пятен. Вторая настоящая особая точка отвергнута алгоритмом вследствие установления параметра Dosobr =60

Несмотря на все меры, описанные выше, иногда ложные особые точки все-таки находятся. Один из подобных случаев можно увидеть на рис. 7.

Как можно видеть, особая точка справа на правом изображении (рис. 7.)с кругом из черных пикселей является ложной. Она была найдена из-за изобилия маленьких пятен с различными цветами (направлениями), количества пикселей, в которых были перемножены. Эти маленькие пятна в программе игнорируются для предотвращения излишнего перемножения количеств пикселей в них. Для реализации этого алгоритма была введена новая так называемая «бордюрная маска», отрабатывающая с большим (или меньшим) размером относительно основной маски.

Эта маска состоит только из одной линии по краю квадрата толщиной в 1 пиксель, являющегося его стороной (линии его «бордюра»). Это можно понять на следующем примере:

Большая маска является бордюрной, меньший квадрат – обычная основная маска со стороной 40. Бордюрная маска больше на величину 15 по всем координатам (в результате сторона этого квадрата 70) (рис. 8). Следующий шаг: программа определяет список всех цветов, попавших в основную маску, и цвета, которые содержатся в бордюрной маске. Все цвета в основной маске должны содержаться и в бордюрной маске для проведения вычислений нормальным образом, как это было описано выше.

а)

б)

в)

Рис. 7 Отпечаток пальца (а), изображение с особыми пятнами (б), особые точки (в).

Если же какой-либо цвет участвует в основной маске, но не встречается в бордюрной маске, следовательно, он представляет собой маленькое пятно, оставшееся после фильтрации и является помехой, на которую внимание обращать не нужно. Такой цвет исключается из расчетов, и то количество пикселей, которое в нем присутствует, добавляется к количеству превалирующего цвета в основной маске. После таких замен в буфере расчета маски (не на самом изображении!) производится вычисление P по обычной формуле. Результат внедрения этого решения можно видеть на следующих изображениях.

Рис. 8. Бордюрная маска на поле направлений

Как можно видеть из рис. 9, программа в этом случае отвергла две ложные особые точки – справа и в самом верху изображения. Большое количество экспериментов показывает, что дополнительное введение бордюрной маски положительно сказывается на исключении ложных особых точек, на отфильтрованном изображении, но часто это не может помочь убрать ложные особые точки на краю отпечатка пальца из-за сложной структуры поля направлений с длинными полосами одного направления – такие полосы проходят в бордюрную маску.

а)                        б)

Рис. 9. Поле направлений с особыми пятнами (а), с особыми точками (б)

Дальнейший алгоритм определяет тип особых точек.

Определение типа особых точек сводится к обходу особых точек на расстоянии o_radius и определении угла поворота по заданной траектории. Угол поворота определяется целыми частями от π . То есть 1,00000 это π , 2,00000 это 2π , -1,0000 - это -π и т. д. Если после обхода угол поворота линий траектории дактилограммы равен 0, то это ложная особенность. При обходе берется значение псевдоугла Ω , изначально равное 0, и при каждом смене направления его значение уве- личивается, или уменьшается в зависимости от того, ярче следующий цвет в поле направлений или темнее. Если яркость меняется более, чем на 3/4 от максимально возможной (перешагивание через п), то это учитывается при суммировании за счет уменьшения (увеличения) псевдоугла на 1 против направления, а затем прибавления оставшейся части цветов (1/4), если это необходимо. При обходе всего круга берутся значения через d9 = 2*^ф*п. После полного обхода полученное число псевдоугла делится на количество направлений в поле N, которое определяется на этапе формировании поля направлений; данное число и поступает в выходной параметр SP как тип особой точки (псевдоугол поворота линий направлений дактилограммы при обходе по часовой стрелке):

П

SP [ n ] = ^

.

Этот алгоритм исполняется с тремя различными радиусами. После этого массив SP[n] будет содержать значение последнего расчета типа особой точки с последним по номеру радиусом.

Как можно видеть на рис. 10 (б) особая точка определилась как спираль (рис. 10 (а) только на наибольшем третьем круге.

Заключение

В данной работе представлен численный метод поиска особых точек дактилоскопических изображений по полю направлений. Метод позволяет определить положение и тип особых точек.

а)

б)

Рис. 10. Определение типа особой точки дактилограммы (а) по полю направлений (б)