Метод получения оптических суперосцилляций на основе трехволновой интерференции

Современные темпы развития технологий приводят к постоянному уменьшению размеров как используемых инструментов, так и создаваемых изделий. Это требует увеличения разрешающей способности измерительной и контролирующей аппаратуры, что, в свою очередь, ведёт к развитию микроскопии. Однако существование фундаментального ограничения разрешающей способности, так называемого «дифракционного предела» [1], существенно ограничивает эту область исследований.

^ d min ~ ,                                                  (1)

2n где dmin – минимальный диаметр пятна, в которое можно сфокусировать электромагнитное излучение, λ – длина волны электромагнитного излучения в вакууме, n – показатель преломления среды, в которой распространяется излучение.

Существует множество способов как уменьшить влияние этого ограничения (использование рентгеновских волн [2, 3], иммерсионная микроскопия [4]), так и полностью его избежать (зондовая микроскопия [5–7]). Одним из способов преодоления дифракционного предела в оптике (получения сверхразрешения как в микроскопии, так и в литографии) является использование оптических суперосцилляций.

Суперосцилляции – это локальные участки в распределении интенсивности, которые имеют характерные размеры деталей существенно меньшие половины длины волны. Другими словами, локально эти осцилляции имеют период меньше периода самых высоких пространственных частот, допустимых диапазоном несущих частот [8, 9].

Первые упоминания о суперосцилляциях в радиоволнах встречаются в 1940-х годах, когда была использована антенна специального вида для фокусировки радиоволн в сколь угодно малую область [10, 11]. Было обнаружено, что лишь малая часть мощности излучения может существовать в виде суперосцилляций, остальная часть приходилась на сильное гало.

В 1952 появилась идея применить подобный интерференционный принцип для получения суперосцилляций в области видимого электромагнитного излучения [12, 13]. И всего несколько лет назад (в 2012 году) оптические суперосцилляции были практически получены с помощью сложения пучков Бесселя и Гаусса [14, 15].

В данной работе предложен другой способ создания оптических суперосцилляций, основанный на интерференции нескольких коллимированных пучков. Проведено теоретическое исследование таких оптических суперосцилляций, получены зависимости их размера и амплитуды от параметров схемы интерференции.

Теоретические основы получения оптических суперосцилляций

Как известно, распределение амплитуды поля при интерференции N когерентных коллимированных источников излучения может быть представлено в виде:

N - -

A = £ A i e ^- iki r i .                                         (2)

i = 1

Здесь k i - волновой вектор i -ой волны, k i = 2 п/ Я . При N = 2 мы получаем синусоидальное распределение интенсивности I = | А |² . Наименьший период этого распределения равен половине длины волны при встречном распространении волн (когда к 1 =- к 2 ). На рис. 1, а показано распределение амплитуды электрического поля волны вдоль оси X и соответствующее распределение интенсивности для случая, когда биссектриса между векторами к 1 = - к 2 параллельна оси Y.

Простейший случай возникновения суперосцилляции наблюдается уже при рассмотрении интерференции трех коллимированных волн. Возьмем три волны с компланарными волновыми векторами, причем волновой вектор третьей волны направлен по биссектрисе угла между первыми двумя волнами. Если волновой вектор 2-ой волны параллелен оси Y, то график распределения амплитуды вдоль оси Х будет иметь вид, показанный на рис. 1, b . Как видим, по сравнению с рис. 1, a график сместился по вертикали на постоянную величину, зависящую от амплитуды этой 3-ей волны. При этом в распределении интенсивности I ( x ) (рис. 1, b ) возникают локальные участки, чей размер, то есть расстояние между двумя нулями, меньше, чем 1 2, а интенсивность существенно ниже, чем у окружающих их пиков. Эти локальные максимумы можно классифицировать как простейший случай суперосцилляций. В связи с этим представляет особый интерес исследование свойств именно этого вида суперосцилляций.

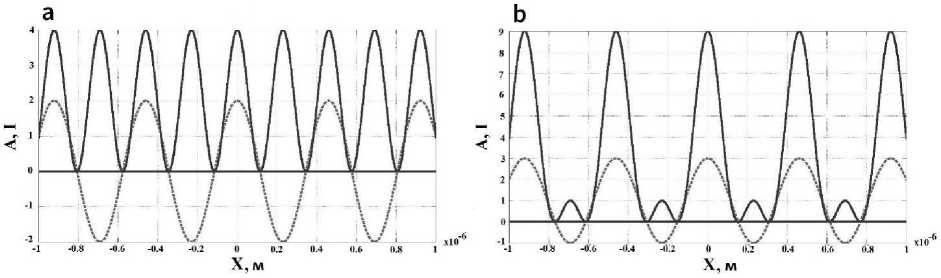
Рис. 1. Распределение амплитуды и интенсивности при интерференции 2-х волн (a) и 3-х компланарных волн (b). Значения амплитуды и интенсивности взяты в условных единицах.

Распределение интенсивности выделено толстой линией

Дополнительной особенностью данного вида суперосцилляций является их повторяемость с малым периодом.

Зависимость размера и амплитуды оптических суперосцилляций от амплитуды одной из интерферирующих волн

Интенсивность и размер оптических суперосцилляций зависят от соотношения амплитуд интерферирующих волн. В данной работе мы исследовали изменения этих параметров при варьировании интенсивности волны, распространяющейся между двумя другими волнами, когда амплитуды этих волн равны между собой.

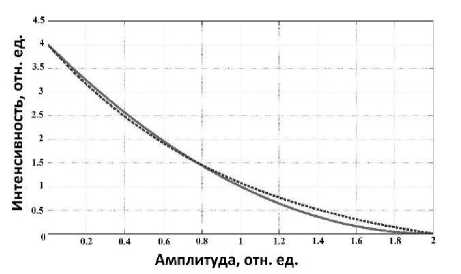
Рис. 2. График зависимости интенсивности оптических суперосцилляций от амплитуды 3-ей волны источника. Сплошная линия соответствует обнаруженной зависимости, пунктирная соответствует аппроксимации

На рис. 2 показан график зависимости интенсивности оптических суперосцилляций от амплитуды 3-ей волны. Можно заметить, что

зависимость имеет вид y = C 1 e

x + C 2 , где C 1

вида C 1 e" x + C 2

суперосцилляции превращаются в обычные интерференционные полосы.

и C ₂ – константы, подобранные так, чтобы концы графиков совпадали. Если рассматривать относительные величины амплитуд, то при А з = 2 и A 1 = А ₂ = 1 оптические суперосцилляции пропадают, так как график распределения А поднимается так высоко над осью абсцисс, что уже не пересекает её. При A 3 = 0 интенсивность оптических суперосцилляций равна 4, то есть квадрату суммы амплитуд 2-х других волн. Это соответствует тому, что оптические

На рис. 3 показан график зависимости размера оптических суперосцилляций от их интенсивности. Можно заметить, что зависимость имеет вид y = C₃ 3 x . Причём, когда размер суперосцилляций стремится к нулю, их интенсивность также стремится к нулю. Когда их интенсивность равна 4, то есть интенсивности обычных интерференционных полос, размер оптических суперосцилляций равен половине длины волны, то есть оптические суперосцилляции превращаются в обычные интерференцион-

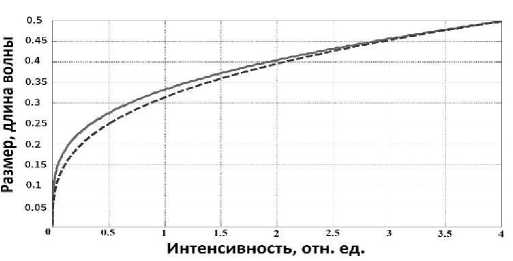
Рис. 3. График зависимости размера оптических суперосцилляций от их интенсивности. Сплошная линия соответствует обнаруженной зависимости, пунктирная соответствует предполагаемой зависимости

ные полосы.

Двумерное распределение интенсивности при интерференции трех волн

В ходе реального эксперимента происходит наблюдение не за одномерным срезом, а за двумерной интерференционной картиной. Поэтому для наглядности была смоделирована 2D интерференционная картина от 3-х плоских волн с компланарными волновыми векторами (рис. 4, a ). На картине видны обычные светлые интерференционные полосы, а посередине тёмных интерференционных полос наблюдаются тонкие светлые полосы, соответствующие оптическим суперосцилляциям.

Однако, если волновой вектор 3-ей волны сместить из плоскости, образуемой волновыми векторами первых двух волн, интерференционная картина потеряет трансляционную симметрию вдоль оси Y. На рис. 4, b показана интерференционная картина, соответствующая случаю, когда проекция волнового вектора третьей волны на исходную плоскость направлена по биссектрисе между волновыми векторами двух других волн. При движении вдоль оси Y наблюдается появление и последующее исчезновение суперосцилляционных полос (тонкие полосы на фоне темных полос). Такое поведение связано с тем, что при движении вдоль оси Y происходит монотонное изменение сдвига фаз между первыми двумя и третьей волной.

На рис. 5 показано, как смещение волнового вектора 3-ей волны из плоскости волновых векторов двух других волн влияет на изменение получаемой интерференционной картины оптиче- ских суперосцилляций. На плоскости XY была выбрана область для моделирования, по OZ откладывалась интенсивность.

Рис. 4. a ) Интерференционная картина от 3-х плоских волн с компланарными волновыми векторами; b ) интерференционная картина от 3-х плоских волн в случае, когда волновой вектор третьей волны выходит из плоскости, образуемой волновыми векторами первых двух волн

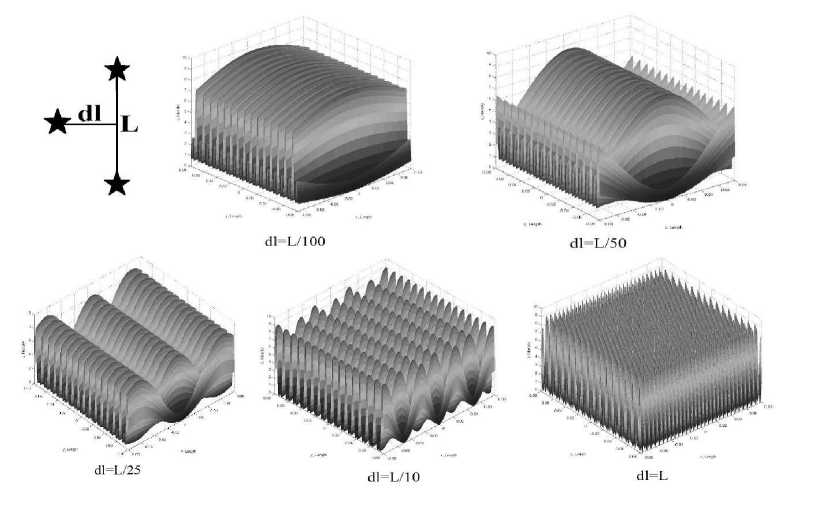
Рис. 5. Зависимость перетекания оптических суперосцилляций в обычные интерференционные полосы от отклонения волнового вектора 3-ей волны от плоскости, образуемой волновыми векторами двух других волн

Как видно из рис. 5, при незначительном отклонении 3-го волнового вектора (отношение проекций k3y I k3 x= 1 I100 ) интерференционная картина слабо изменяется в пространстве. Но при увеличении этого расстояния на исследуемом участке увеличивается количество переходов оптических суперосцилляций в обычные интерференционные полосы. В итоге, все три волны попарно интерферируют между собой и интерференционные картины накладываются друг на друга.

Заключение

Исследован метод получения оптических суперосцилляций, основанный на интерференции от трёх коллимированных волн. Получены следующие результаты:

• 1)    зависимость интенсивности оптических суперосцилляций от амплитуды 3-ей волны источника имеет экспоненциальный вид;

• 2)    зависимость размера оптических суперосцилляций от их интенсивности имеет вид корневой зависимости.

Дрязгов М.А., Свиридова И.В., Метод получения оптических суперосцилляций Исаков Д.С., Микляев Ю.В. на основе трехволновой интерференции

• 3)    получены распределения интенсивности света, соответствующие интерференции компланарных и некомпланарных волн, обеспечивающие возникновение как одномерных, так и двумерных суперосцилляций; обнаружено исчезновение суперосцилляций при удалении от некомпланарной ориентации волновых векторов.