Метод полурешетки идентификаторов для тестового диагностирования функциональных узлов микропроцессоров

Тестовое диагностирование функциональных узлов микропроцессоров во многих случаях осуществляется с помощью двух типов тестов: проверяющего теста и теста поиска дефектов (ТПД), обладающих различной длиной, глубиной поиска дефектов и сложностью процедуры дешифрации результатов прохождения теста. Если к проверяющему тесту не предъявляются жесткие требования по длине, а к ТПД - по простоте дешифрации, то эти два теста можно объединить в один. При этом возникает задача сохранения идентификаторов власов эквивалентных дефектов (КЭД) для обеспечения взаимооднозначного соответствия между КЭД и его идентификатором и, кроме того, уменьшения длины ТПД. Решение такой задачи возможно с помощью ТПД, сформированных по новому методу построения идентификаторов и ТПД, изложенному в данной работе.

Особенность предложенного метода состоит в том, что идентификаторы по различающем функциям строятся не для всех КЭД схемы ki G В(Ку а только для некоторого мини мального подмножества из В(К), необходимого для построения всех остальных идентификаторов. Входные наборы таких идентификаторов образуют множество, состоящее из двух подмножеств. В первое подмножество входят наборы, на которых при отсутствии дефектов из В(К) равны нулю, а в другое подмножество -наборы, на которых реакции равны единице. Первое подмножество образует нулевую выходную последовательность, а второе - единичную выходную последовательность. Номера входных наборов с искаженными реакциями позволяют осуществить поиск дефектов.

При разработке метода построения ТПД были введены следующие ограничения:

-комбинационная схема имеет один выход,

• -число элементов и связей в схеме с дефектами не увеличивается,

• -схема построена на двухвходовых элементах И, И-НЕ, ИЛИ, ИЛИ-НЕ,

  -возможны однократные дефекты, моделируемые однократными константными дефектами типа константа 0 и константа 1.

Следует заметить, что приведенные ограничения не являются обязательными. Поясним метод полурешетки идентификаторов с помощью диаграммы, приведенной на рис.1.

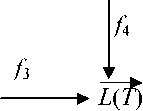
Рисунок 1. Диаграмма, отображающая процедуру построения

По графу моделирования дефектов определяется множество К*, для которого строятся идентификаторы. Например, для бесповторной комбинационной схемы типа дерева — это множество висячих вершин. Отображение /, означает, что для каждого КЭД из множества К* строится различающая функция, по которой определяется соответствующий КЭД идентификатор [2]. Напомним, что под идентификатором КЭД понимается множество входных наборов, на которых проявляются дефекты из данного класса, а также между КЭД и его идентификатором существует взаимооднозначное соответствие. Множество идентификаторов для КЭД из множества К* образует множество L*(T). Отображение Ц показывает, что множество К* является подмножеством множества всех КЭД схемы В)К), а множество L*(T) является подмножеством ЦТ). Особый интерес в рассматриваемой диаграмме на рис.1 представляет отображение /з: В(К) ~^В{К), смысл которого состоит в определении частичного порядка [6] на множестве В(К). Также частичный порядок задается и на множестве ЦТ). Отображение Д означает, что существует взаимооднозначное соответствие между КЭД из множества В(К) и идентификаторами из множества ЦТ), которые и являются ТПД по методу полурешетки идентификаторов.

Порядок на множестве В^К) в диаграмме на рис.1 непосредственно вытекает из моделирования КЭД, которое может быть полным и неполным.

Определение 1 . Будем говорить, что кратный дефект Ц с ВЦС) полностью моделирует КЭД к; в том случае, если одновременно выполняются два условия: функции, реализуемые КС при наличии к. и Ц равны, т.е. Цк}) = z(^) к! е к_ь

Иными словами моделирование полным, если оно определено на всем множестве X входных наборов схемы.

Определение 2 . Моделирование называется неполным при определении его на некотором подмножестве множества X.

В дальнейшем под моделированием будем понимать полное моделирование. Выполнение условия Z(Ke) = Z(Ke) свидетельствует об эквивалентности ке и Ке , т.е. ке = Ке. С учетом этой эквивалентности зададим множество В(К) частичный порядок: кп < к , если и только если кп £ Ке и ке = Ке ; кп = ке , если и только если кп = ке. Для дальнейших рассуждений частично-упорядоченное во В (К) удобно представить в виде графа моде- лирования.

Определение 3 . Графом моделирования назовем граф, в котором вершины соответствуют КЭД из множества В(К) , а ребра связывают КЭД, находящийся в отношении моделирования.

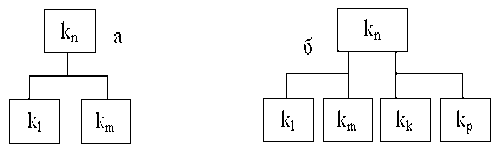
Рисунок 2. Конструкции графа моделирования

Граф моделирования строится с использованием двух конструкций, приведенных на рис.2.

В первом случае (см. рис.2,а) к моделируемому классу дефектов к_л подходит одно ребро. Значит возможен только один вариант моделирования к_л = К_л , где К_л = {к_е, к_т} . Во втором случае к к_л подходят два ребра или более (см. рис.2, б) и возможны два или несколько вариантов моделирования: к_л = К_л и к^ = К_л , где К_П )кь кт) и К_л— {^п > ^р} • Именно в применении указанных конструкций и заключается отличие графа моделирования от дерева дефектов [2] , по которому установление моделирования между КЭД без использования дополнительной информации (не содержащей в дереве), в общем случае, невозможно. Таким образом, граф моделирования можно построить из дерева дефектов путем преобразования ребер с учетом конструкций рис.2. Приведенное определение и описание графа моделирования позволяет сформулировать следующее утверждение:

Граф моделирования полностью описывает моделирование классов дефектов.

Действительно, по построению и в дереве дефектов и в графе моделирования ребрами связываются вершины, отображающие те

КЭД, для которых существует общий путь от одного из входов до выхода КС. А так как применение в графе моделирования конструкций, приведенных на рис.2, позволяет полностью установить отношения моделирования между вершинами, связанными ребрами, то для доказательства утверждения необходимо доказать, что в отношении моделирования могут быть лишь КЭД, имеющие общий путь. Пусть кратный дефект К_е , состоящий их КЭД к_т и к_п осуществляет полное моделирование однократного КЭД к_е , но при этом в схеме не существует пути от одного из входов до выхода КС, проходящего одновременно через место нахождения КЭД к_е и к_т или к_е и к_п . Обозначим через Х_е ,Х_т,Х_п множество входных наборов, являющихся проверяющими для КЭД к_е , к_т , к , соответственно. Следовательно, имеем непустое множество Q(_m U Х^ П Х_е , так как из определения полного моделирования множество Х_е бу дет множеством всех проверяющих наборов для кратного дефекта К_е . Тогда 3t,t £ (Х_т U Х^ П Xg , являющийся проверяющим одновременно для КЭД к_е и к_т или к_е и к_п . Значит путь, активизируемый этим набором, проходит одновременно через место нахождения к_е и одного из к_п , к_т . Пришли к противоречию. Следовательно, наше предположение неверно, а, значит, в отношении моделирования могут быть лишь КЭД, для которых существует общий путь от одного из входов до выхода КС.

Частично-упорядоченное множество В(К) , определяемое отображением д\ РЛЮ -> В(К) и задаваемое графом моделирования, можно представить в виде верхней полурешетки [6] (В(К), U) , т.е множества В(К) и определенной на нем операции объединения U. Действительно поскольку К_е содержит моделирующие к_е классы дефектов К_е = к_е U K_tl) ... U к_п и к_е = К_е, то к_е можно представить как к_е = к_к U К; U ... U к_п. В то же время КЭД выхода КС являются верхними гранями двух подмножеств, на которые разбивается множество В(К) в соответствии с графом моделирования. Представление множества В(К) в виде (B(K),U) позволяет сформулировать следующее утверждение:

Если к_е = к_к U к, U ... U к_п, то а_е(Т) = «„.(Г) U «ДТ) U ... U а_п(Т).

Действительно, пусть имеем а_е(Т) ⁼ а_к(Т) U аДТ) U ... U а_п(Т\ Докажем, что он является идентификатором для к_е. Любой идентификатор выполняет две задачи: создает в месте дефекта значение сигнала, инверсное значению дефекта, и активизирует путь прохождения сигнала от места дефекта до выхода

КС. Следовательно, ^ а₇(Т), а₇(Т) £ а_е(Т^ будет проверяющим для КЭД к_е, так как к_е находится на активизированном пути. Значит К сд(Т), aj(T) £ сс_е(Т) => у_е ^ у, т.е выполнено первое условие определения идентификатора.

Для любых неэквивалентных КЭД к_е , к_т можно построить моделирующие их кратные дефекты К_е и К_т, при этом они отличаются хотя бы одним составляющим дефектом к_к, так как в противном случае к_е = к_т и они эквивалентны. Пусть к_к £ К_е и к_к £ К_т . Значит а_к(Т) £ а_е(.Т), а_к(Т) £ a_m(T) и на сгДТ) Уе * Ут Х.е. выполнено второе условие определения идентификатора. Таким образом а_е(Т) = ct_K(T) U «[(Т) U ... U а_п(Т) является идентификатором ДЛЯ Kg .

По сути дела, проведенные рассуждения определяют отображение h‘.L(T) -> L(T), позволяющее построить множество L(T). которое и является ТПД. Перейдем к рассмотрению построения множества К*.

Множество К* формируется таким образом, что соответствующее ему множество L~ (К) содержит все входные наборы, необходимые для построения любого а_е(Т) £ L(T). Иными словами, любой к_е £ В (К) должен моделироваться некоторым подмножеством из К*. Моделирование однократного дефекта кратным (подмножеством из К*) имеет направленный характер. Так в бесповторной КС типа дерева моделирование осуществляется по направлению от КЭД, соответствующих подключенным ко входам схемы элементам, к КЭД, соотсетст-вующим выходу. Назовем такое моделирование прямым. В произвольных КС, кроме прямого моделирования в древовидных подсхемах, существует обратное моделирование, при которых КЭД узла разветвления моделируется КЭД линий разветвлениях [2]. Сформулируем следующее утверждение:

В бесповторной КС типа дерева множество КЭД висячих вершин графа моделирования, соответствующих подключенным ко входам схемы элементам, образует множество К*.

Действительно, поскольку множеству всех висячих вершин графа моделирования соответствуют все возможные пути от входов до выхода КС, то для любого КЭД к_е можно построить моделирующий его кратный дефект К_е = к_к V) K_t\J ... U к_п, а значит, согласно приведенным выше рассуждениям и идентификатор, где V- Kj , Kj £ К_е - висячая вершина графа моделирования. Таким образом, множество КЭД висячих вершин графа моделирования образует множество К*.

В произвольной КС множество К* строится следующим образом. В схеме выделяются максимальные древовидные подсхемы [2], для каждой из которых К* рассмотренным выше способом. Объединение К* всех выделенных подсхем и образует К* схемы.

Оценим эффективность метода, сравнив для бесповторной КС типа дерева известный и построенный метод по числу КЭД, для которых и идентификаторы строятся по различающим функциям. Для известного метода [2] это число оценивается как 2(п+1). Для оценки построенного метода сформулируем следующее утверждение:

Для бесповторной КС типа дерева с п элементами множество К*

• 1,5    (п + 1),п — нечетное;

• 1,5    (n + 1) — 0,5 п — четное.

Действительно, мощность множества К* равна числу висячих вершин графа моделирования. Покажем, что при нечетном п выполняется | К* | = 1,5 (п + 1).   п=1,3,5    |К*| =

1,5(1 + 1) = 3, |К*| = 1,5(3 + 1) = 6, |К*| = 1,5(5 + 1) = 9, соответственно, и совпадает с числом висячих вершин графов моделирования. Пусть формула справедлива при n = i, т.е. |К*| = l,5(i + 1). Покажем, что она справедлива при n = i + 2. Учитывая, что увеличение числа элементов бесповторной КС типа дерева на 2, приводит к увеличению числа висячих вершин графа моделирования на 3, имеем |К*| = l,5(i + 1) + 3 = l,5i + 3 + 1,5 = l,5(i + 2) + 1,5 = 1,5[(i + 2) + 1] , а так как n = i + 2, то |K*| = l,5(n + 1). Покажем, что при нечетном п мощность множества К* равна |К*| = 1,5 (n + 1) - 0,5. При п = 2,4,6 |К*| =

1,5 (2 + 1) - 0,5 = 4,     |7Г | = 1,5 (4 + 1) -

0,5 = 7, |7Г | = 1,5 (6 + 1) - 0,5 = 10, соот ветственно, и совпадает с числом висячих вершин графов моделирования. Пусть формула справедлива при n = i. т.е. |К*| = 1,5 (i + 1) — 0,5. Покажем, что она справедлива при n = i + 2. Имеем |К*| = 1,5 (i + 1) — 0,5 + 3 = l,5i + 3 + 1,5 - 0,5 = l,5(i + 2) + 1,5 -0,5 = 1,5 [(i + 2) + 1] — 0,5 , а так как n = i + 2, то|К*| = 1,5 (n + 1) - 0,5.

Таким образом, оценка эффективности будет иметь следующий вид

3(п + 1)3

—---— = - п — нечетное

4(n + 1)4

3(n + 1) - 13

------—— < — п — четное 4(n + 1)4

Так как в силу предложение 3 [2] в бесповторной КС типа дерева для каждого КЭД существует простой идентификатор (т.е. идентификатор, состоящий из одного входного набора), то приведенная оценка будет оценкой и длины теста.

• Пример 1 . Рассмотрим построение множества К* для КС рис.З.

Построений по ДД с учетом конструкций рис.2 граф моделирования этой схемы представлен на рис.4. Выделим из схемы мак симальные древовидные подсхемы, показанные на рис.5. Соответственно, граф моделирования разобьется на четыре подграфа рис.б. Тогда, множество К* составят КЭД висячих вершин этих подграфов, т.е. К* = (2Х, 40,50,6Х, 7Х, 9Х, 140,150,17Х}.

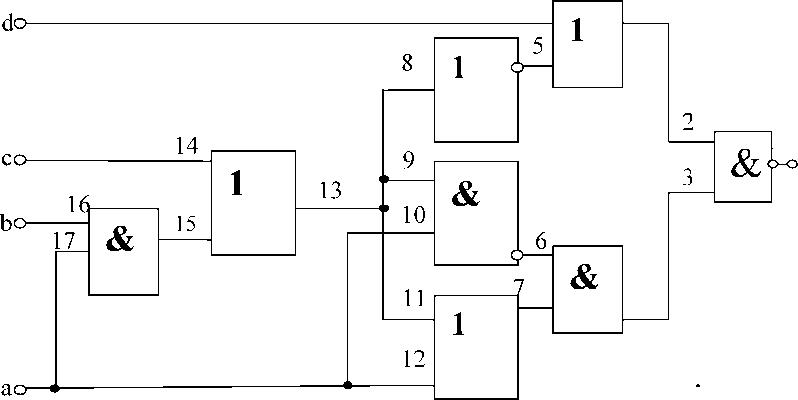
Рисунок 3. Схема к примеру 1.

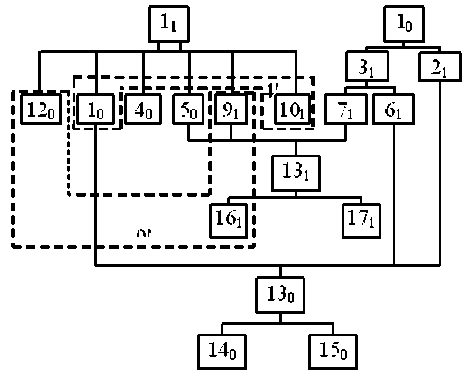
Рисунок 4. Граф моделирования для схемы на рис.З.

Тест поиска дефектов предлагается строить в виде такой последовательности входных наборов идентификаторов, что на ней образуется нулевая и одиночная выходные последовательности. При этом входные наборы теста поиска дефектов составляют основание полурешетки идентификаторов.

Определение 4 . Полурешеткой идентификаторов назовем множество 7(7) с определенной на нем операцией и . Под основанием полурешетки будем понимать минимальное подмножество идентификатор 7~(7) с 7(7) такое, что для любого к_е Е К найдется подмножество «Д7) с L~(T\ которое является идентификатором к_е.

В отличие от поиска дефектов в [2], представляющего собой процедуру с остановкой, в предлагаемом методе тест пропускается до конца, после чего производится дешифрация результатов происхождения ТПД.

Использование прямого моделирования для построения множества 7(7) состоит в вычислении идентификатора моделируемого КЭД по уже известным идентификаторам моделирующих КЭД. Основную трудность представляет нахождение идентификаторов моделирующих КЭД при обратном моделировании. Эти идентификаторы могут быть найдены либо путем непосредственного вычисления по различающей функции [2], либо выделением из идентификатора уже известного моделируемого КЭД. В соответствии с этим, существует два способа построения множеств 7(7) и К*.

В основе первого способа лежит прямое моделирование в бесповторных КС типа дерева. Множество К* по множеству В(К), заданному в виде графа моделирования, определяется как множество висячих вершин.

Построение множества 7(7) при первом способе состоит в вычислении идентификаторов для каждого к_е £ К* по различающей функции Ф_е и в объединении вычисленных идентификаторов на основании прямого моделирования в выделенных подсхемах. Построение 7(7) удобно осуществлять с помощью графа моделирования. В графе вместо КЭД из В(К) в соответствующие вершины помещаются вычисленные идентификаторы. В вершину моделируемого КЭД помещается объединение идентификаторов моделирующих КЭД. Объединение идентификаторов для всех КЭД схемы образуют множество 7(7).

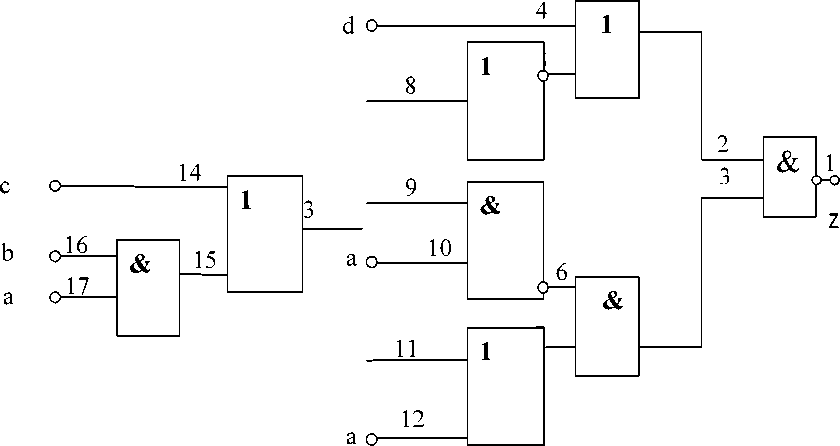
Рисунок 5. Подсхемы для схемы на рис.З.

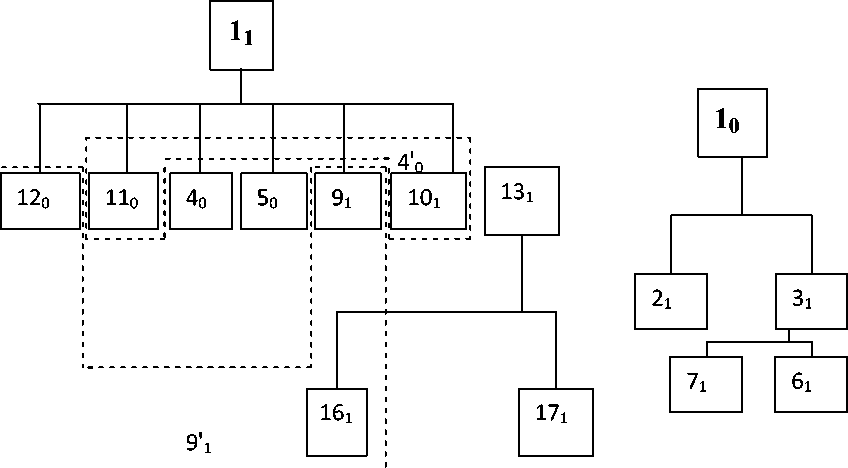
Рисунок 6. Граф моделирования для подсхем на рис.5.

Тест поиска дефектов получается из множества L~(T\ Сначала L~(T) преобразуется таким образом, что каждый входной набор содержится в L~(T) только один раз, т.е. происходит удаление повторяющихся в два поля входных наборов. После этого входные наборы группируются в два поля: поле нулей и поле единиц, причем в поле нулей (поле единиц) помещаются те входные наборы, на которых выходной символ КС без дефекта равен 0(1). Такой подход позволяет упростить подготовку ответных реакций КС при дешифрации результатов происхождения теста. Наконец, в полученном тесте происходит нумерация входных наборов.

Пример 2 . Для КЭД из К* (см. пример 1) по различающим функциям стоятся идентификаторы, приведенные в табл.1. Построение множества ЦТ) поясняется рис.3.3,в, на котором в вершины графа моделирования помещены входные наборы идентификаторов, причем входные наборы идентификаторов, причем входные символы набора сверху вниз сопоставлены входными буквами a, b, с, d, соответственно. Тест поиска дефектов, полученный из множества L~(T) (см.табл.1), приведен в табл.2. На рис.7 показана полурешетка идентификаторов для подсхем на рис.5.

К отличным особенностям первого способа построения множества ЦТ) и теста поиска дефектов можно отнести следующее. Во-первых, непосредственное (без дополнительных преобразований) использование различающей функции, что позволяет сделать процедуру построения теста достаточно простой. Во-вторых, не минимальность мощности множества К*, вследствие чего тест имеет не минимальную длину.

Если при поиске идентификаторов в КС с разветвлениями использовать только прямое моделирование и не выделять максимальные древовидные подсхемы, то процедура построения остановится на КЭД узлов разветвлений, так как некоторые идентификаторы для КЭД линий разветвлений будут неопределенны, и дальнейшее использование прямого моделирования, по этой причине, невозможно.

Для построения идентификаторов КЭД линий разветвлений во втором способе используется обратное моделирование и осуществляется выделение, если оно возможно, искомых идентификаторов из уже известного идентификатора КЭД узла разветвления. Если для некоторого КЭД выделить идентификатор по какой-либо причине невозможно, то тогда он строится по различающей функции.

Таблица 1 — Множество L~(T)
Идентификаторы КЭД из множества							к*
Класс дефектов		2i	40	5о	61	7.	9.	14о	150	17.
	а	0	0	1	1	0	1 1	1 0	1 1	0
Иденти-	ь	1	1	0	1	0	0 0	0 1	1 1	1
фикатор	с	1	1	0	1	0	0 0	1 1	0 0	0
	d	0	1	0	1	1	1 0	0 1	0 1	1

Таблица 2 - Тест поиска дефектов

Тест поиска дефектов
Номер входного набора	123456789 10
а b с d	0   0 0    1 1 1    1    0 1    1 110 1110 10 0 1   0 0   1 0 0   1    1 0   0 0 11110 0 10 1
Реакция КС без дефекта	0 0 0 0 0 0 0 1 1 1

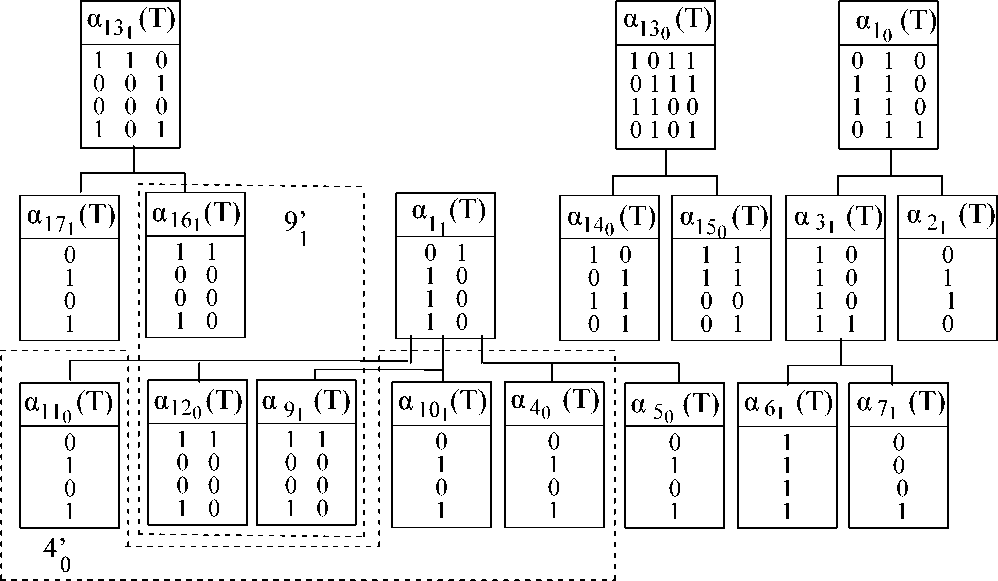
Рисунок 7. Полурешетка идентификаторов