Метод порождения графов с контролем статистических свойств
Автор: Бишук А.Ю., Зухба А.В.
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Математика
Статья в выпуске: 3 (63) т.16, 2024 года.
Бесплатный доступ
В работе предлагается метод условного порождения графов, учитывающий статистические характеристики графов. Данные характирстики разделяются на две группы. Первая группа, называемая простыми статистиками, может быть вычислена эффективными детерминированными алгоритмами со сложностью не более квадратичной от числа вершин. Такое разделение диктуется дороговизной использования вычислительно сложных алгоритмов на графах, по размеру приближенных к реальным. Вторая группа характеристик порождается в скрытом пространстве и отвечает за закономерности графа, которые невозможно описать «простыми статистиками». Этот подход позволяет порождать графы с точно заданными статистическими характеристиками, при этом сохраняя их разнообразие. Более того, данный метод может быть применен для порождения графов, имеющих схожую структуру с исходным. Работоспособность предложенного метода подтверждается вычислительным экспериментом, проведенном на датасетах Citeseer и Cora.
Порождение данных, порождение графов, графы, вариационный автокодировщик, теория графов, генеративные модели, условное порождение, вариационный вывод
Короткий адрес: https://sciup.org/142243258
IDR: 142243258 | УДК: 519.25,
Текст научной статьи Метод порождения графов с контролем статистических свойств
Проблема сложности получения большого числа данных для обучения нейросетевых моделей становится все более актуальной. Особенно это заметно в задачах, где данные представлят собой графовые структуры. Для решения этой проблемы часто используются подходы по порождению данных [4].
Кроме того, часто возникает потребность в графах, имеющих схожее распределение с исходным. Это важно, например, в случае графа ежедневных контактов фиксированного сообщества, где необходимо порождать ряд графов, похожих на изначальный. Для этой задачи традиционно используются генеративные модели, такие как GraphVAE [5] или диффузионные [6].
Однако существующие методы [14], [15] фокусируются на реконструкции исходного графа и не способны учитывать при порождении интуитивно понятные характеристики. Например, в случае графа контактов время взаимодействия людей в офисе ограничено, а потому есть ограничения на время и число контактов. Предлагается использовать в качестве ограничения на порождение не столько качество реконструкции, сколько заранее выбранные глобальные характеристики графа (например число ребер, вершин, кластерное число и так далее). Тем самым порождаются графы с заранее выбранными статистиками и имеющие распределение, схожее с исходным графом.
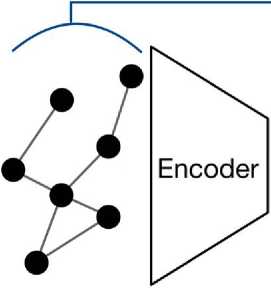
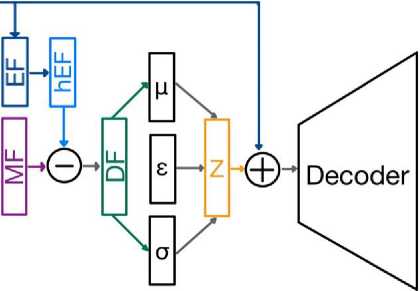
Рис. 1. Схема предложенного метода. Здесь MF — векторное представление графа, EF — вектор статистик из теории графов, hEF — преобразованный вектор EF, DF — вектор, содержащий информацию о графе, которую невозможно получить преобразованием предпосчитаппых статистик графа, s — случайна я величина € N (0,1), a Z — матрица из распределения N (д, ст)
Предложенный в данной работе метод может быть использован для поиска «сложных» статистик графа, таких как цикл максимальной длины или центральность смежности вершин [7], поиск которых до сих пор остаётся нерешенным на достаточно высоком уровне. Это может быть сделано путем контроля фокуса обучения сети на таких сложных характеристиках графа, если добавить в группу простых статистик больше независимых характеристик.
Первое упоминание идеи использования дополнительной информации для порождении данных встречается в статье «Learning Structured Output Representation using Deep Conditional Generative Models» [13], где была представлена модель Conditional Variational Autoencoders (CVAE). CVAE — это модификация VAE, которая может порождать данные с заданными условиями. В стандартном вариационном автокодировщике (VAE) модель порождает данные на основе скрытого пространства, которое не зависит от каких-либо внешних переменных. В CVAE модель использует дополнительную информацию для порождения данных. Авторы в статье показывают, как CVAE может быть использована для порождения изображений с заданными свойствами. Они используют MNIST [11] для порождения цифр с определенными свойствами, такими как цвет и положение цифры на изображении. Также описывается, как CVAE может быть использована для классификации изображений. Например, авторы статьи применяют CVAE к задаче классификации CIFAR-10 [12], показывая, что CVAE может значительно улучшить точность. Впоследствии было предложено множество модификаций идей CVAE, таких как AC-GAN (Auxiliary Classifier GAN) и InfoGAN (Information Maximizing GAN), которые используют схожие идеи для порождения изображений с более сложными свойствами.
Для иллюстрации работы предложенного метода проводится ряд вычислительных экспериментов для задачи порождения графов с заданными статистиками на примере да-тасетов Cora [9] и Citeeser [10]. Также проводится теоретический анализ предложенного метода, подтверждающий работоспособность предложенного метода, а также схожих эвристических методов [16].
2. Постановка задачи
Пусть задано множество графов {Gi} фиксированного размера по числу вершин п. Каждый элемент задается матрицей смежности A и матрицей признаков вершин V f. Необходимо породить графы, близкие к исходным по статистическим свойствам.
В ходе решения проблемы порождения возникают две задачи — задача правильного восстановления матрицы смежности из скрытого пространства и задача построения неизвестного распределения данных.
Задача реконструкции. Для того чтобы обучить модель порождать новый элемент данных, необходимо научиться реконструировать объект из скрытого пространства. В работе будет предсказываться наличие и отсутствие ребра в графе.
Формально постановка этой задачи может быть описана следующим образом.
Дано: граф G с матрицей смежности A Е Епхп, г де A ij = 1, если ребро (i,j ) существует в графе, и 0 в противном случае. Матрица признаков вершин Vf Е ВАхк, а также набор скрытых ребер Е = {(i,j)}. Здесь k — размер вектора признаков вершин.
Задача
Построить модель, предсказывающую наличие ребра в графе на основе признаков вершин и существующих ребер. Однако особый интерес представляет предсказание наличия маркированных ребер. Задача может быть сформулирована как задача бинарной классификации: для каждой пары вершин i и j нужно предсказать вероятность того, что ребро (i,j ) существует в графе, то есть принимает значение 1 в матрице смежности.

Рис. 2. Процесс маркировки ребер при порождении и тестировании модели
Модель обучается на данных, которые представляют собой множество пар вершин с маркированными и немаркированными ребрами. Она должна определить, какие признаки графа могут помочь в предсказании наличия ребер. На основе этих признаков необходимо построить модель, которая может классифицировать каждую пару вершин в графе.
Результатом работы модели является матрица предсказанных вероятностей существования ребер между всеми парами вершин в графе, включая немаркированные ребра.
Задача порождения. Задача по получению новых графов из неизвестного распределения выглядит следующим образом.
Дано: множество { А г^О Е Епхп матриц смежности графов Gi из неизвестного распределения x(G), построенного на. основе графа. G.
Задача
Получить распределение tt(G) в целях оценки tt(G) для ново го графа G и порождения новых графов из распределения tt(G).
Задача, решаемая в работе. В отличие от ряда работ [17], [18], где для создания алгоритма порождения графов решаются только задачи реконструкции и порождения, в данной работе дополнительно решается задача сохранения характеристик исходного графа.
Для удобства обозначений введем следующие понятия:
Определение 1. Простые статистики в предложенном методе — это числовые характеристики используемые в теории графов, которые могут быть вычислены не более чем за квадратичное время.
В качестве простых статистик графа были выбраны следующие характеристики:
-
• Размерные показатели [0(1)]:
-
- число ребер,
-
— число вершин.
-
• Вершины специального вида [ O(V )]:
-
— изолированные вершины — вершины без единого ребра,
-
— висячие вершины — вершины с одним ребром,
-
— промежуточные вершины — вершины с двумя ребрами,
-
— вершины, связанные с каждой вершиной графа.
-
• Статистики на степенях вершин [ O(V )]:
-
— максимальная степень вершины,
-
— средняя степень вершины,
-
— медианная степень вершины,
-
— модальная степень вершины,
-
— стандартное отклонение степеней вершин в графе.
-
• Гистограмма степеней вершин графа [ O(V )] (здесь ц — средняя степень вершин в графе, & — среднеквадратичное отклонение степеней вершин в графе). Доля вершин со степенью на интервалах: (ц — а,ц), (ц, ц + &), (ц — 2&,ц — &), (ц + &,ц + 2&), (ц — 3& ц — 2&). (ц + 2щ ц + 3&).
-
• Оценка размера наибольшей клики в графе [O(Vd2), d — максимальная степень вершины] [2].
-
• Коэффициент кластеризации [ O(V 2)] [3].
Определение 2. Смешанными статистиками назовем любое численное описание графа, которое однозначно описывает граф.
Под скрытым представлением обычно понимают сжатое представление входных данных, которого достаточно для их восстановления.
Определение 3. Сложными статистиками назовем вектор d, такой что каждая компонента вектора d статистически независима от компонент вектора простых статистик s, и при этом вектор смешанных статистик m выражается через d и s линейно.
Иными словами, под сложными статистиками будут пониматься те особенности графа, которые невозможно выразить при помощи простых статистик.
Введем поняние распределения графа. Допустим, структура графа задается матрицей смежности A G Bnxn. Сопоставим графу матрицу Р G Rnxn, в ячейке (i,j ) которой находится вероятноств того, что значение в матрице A в ячейке (i,j ) изменит свое значение на противоположное. Величина вероятности может отличаться для исходных единиц и нулей или основываться на структурных особенностях графа, но в данной работе они выбирались одинаковыми для всех ячеек и были достаточно небольшими, чтобы порождать по большей части графы, похожие на исходный. Таким образом, порождение графа, похожего на данный (например, имеющий одно линшнее ребро), будет более вероятным событием, чем порождение близкого к обратному.
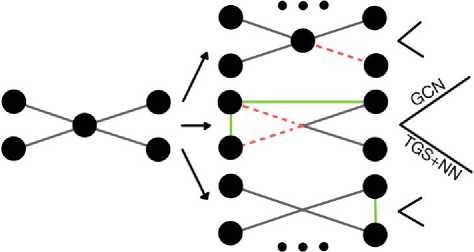
Скрытое представление графа, полученное при помощи GCN
Представление графа на основе простых статистик
Рис. 3. Процесс создания распределения графа па основе имеющегося
Таким образом, отождествляется скрытое представление графа со смешанными статистиками. Также простые статистики переводятся в некоторое скрытое пространство линейной сверткой, требуя, чтобы получившееся представление имело нормальное распределение с нулевым математическим ожиданием, а линейные комбинации его компонент наилучшим образом приближали смешанные статистики в скрытом представлении графа. Под распределением скрытых представлений (они же смешанные статистики) и распределением простых статистик будем понимать множество скрытых представлений и векторов простых статистик, соответствующих графам из распределения графа G.
Подводя итог, задача, решаемая в этой работе, состоит в том, чтобы, подавая в порождающую модель графы из распределения графа G с их векторами простых статистик, получать представления, на основе которых при помощи вектора простых статистик исходного графа породить граф, схожий с исходным.
3. Предлагаемый метод
Предложенный метод порождения графов основан на модели графового вариационного автокодировщика (GraphVAE). В основе данного метода лежит аппроксимация апостериорного распределения матриц смежности графов р(А\Х ). Вводится предположение, что процесс порождения графов и соответствующих матриц смежности зависит от скрытых переменных Z. Для оценки апостериорного распределения с учетом скрытой переменной Z используется вариационное распределение q(Z |Х, А), приближающее распределение p(Z |Х, А). Итоговая вариационная нижняя оценка:
PvAE = Eg(Z|X, A) logp(A|Z) - DKLq(Z\X, A)||p(Z), где A — матрица смежности, Z — матрица скрытых переменных, X — матрица признаков вершин, q(^,p(^) — соответствующие распределения.
Основным преимуществом нового подхода является возможность контролировать порождение, задавая определенные свойства графа. Это делает его более удобным и гибким по сравнению с обычным VAE.
3.1. Описание метода
Идея описываемого метода основывается на выводах, что использование дополнительной информации улучшает качество порождения данных. В качестве дополнительной информации используются простые статистики, посчитанные на исходном графе. С этой точки зрения предложенный метод можно назвать самоусловным GraphVAE по аналогии с CVAE, в котором оптимизируется следующий функционал:
CcondVAE = E,(z|x,c)[log р ( X \ Z ,c)] - D kl [Q( Z \ X ,c) \ P( Z \ c)], где c — дополнительная информация, которая накладывает ограничения на модель.
Алгоритм 1 Алгоритм обучения порождающей модели
Require: G — граф. G = ( A — Матрица смежности, V — Признаки вершин)
Ensure: A — матрица смежности реконструированного графа.
-
1: s o — DeterministicAlgo(G') > Расчет простых статистик исходного графа
-
2: for i ill [1. 2. ...] do
-
3: G[i] — Sam'pleFromDis-tribwtion(G') > Получение графа из распределения
исходного графа
-
4: s [i] — DeterministicAlgo(G') > Расчет простых статистик семплированного графа
-
5: end for
-
6: MF — Encoder(G) > Вычисление матрицы смешанных статистик
-
7: hEF — LL( s ) > Вычисление оценки смешанных статистик
-
8: DF — LL( MF - hEF ) > Выделение сложных статистик
-
9: ц — GCN( DF ), a — GCN( DF ), г — N (0,1)
-
10: Z —— ц + г • (Г
-
11: Z — LL((Z) + LL(so)) > Учет простых статистик при декодировании
-
12: A — Decoder( Z ) > Преобразование порожденной матрицы в матрицу смежности
Следующим шагом алгоритма происходит вычитание оценки смешанных статистик (hEF), полученной линейным преобразованием простых статистик, из самих смешанных статистик (MF). Тем самым в скрытом представлении остаются только те характеристики графа, которые нельзя линейно выразить через простые. Такие характеристики мы называем сложными статистиками (DF).
Далее на основе матрицы сложных статистик (DF) формируется оценка математического ожидания (ц) и дисперсии (г) сложных статистик исходного графа. Затем, при помощи трюка репараметризации, происходит порождение матрицы сложных статистик (Z). Путем сложения полученной матрицы сложных статистик и преобразованного вектора простых статистик исходного графа (so) будет получена итоговая матрица признаков графа (Z), с помощью которой блок декодера формирует матрицу смежности.
Итоговая функция потерь для предложенной модели имеет следующий вид:
1 N N
L(Y, Y, M, s, D) = - N ^^ wij Y log (Y^) + (1 - Yj) log (1 - Y^)]- i=0 j=0
1 N
-Dkl(D, N(0,1)) - N £ £(Mij - sj)2, где
• Y — матрица смежности входного графа;
• Y — матрица смежности порожденного графа, где в ячейке Yij стоит вероятность того, что существует ребро между вершинами i и у;
• M — матрица смешанных статистик;
• s — вектор простых статистик входного графа;
• D — матрица порожденнв1х сложнв1х статистик;
• Wij — веса перед элементами в матрице смежности. Самый болвшой вес у маркирован-HBix ребер, затем у маркированных мест, где ребра нет, меньший вес у существующих не маркированных ребер и самый маленький вес у мест, где ребер нет и они не маркированы. Вес зависит от того, было ли место в матрице маркировано и сколько всего ребер есть в рассматриваемом графе.
3.2. Анализ предложенного метода
Вариационный автокодировщик (VAE) — это генеративная модель, которая обучается отображать объекты в заданное скрытое пространство, после чего порождать новые объекты из этого скрытого пространства.
Часто важно, чтобы элементы скрытого пространства были распределены стандартно нормально. В данной работе это достигается стандартизацией скрытого представления по всем скрытым представлениям, полученным от преобразованных графов.
Далее в этом разделе под простыми статистиками будем понимать скрытое представление простых статистик, которое также будет иметь нормальное распределение с нулевым математическим ожиданием. Это будет достигаться теми же способами, которые используются для получения нормально распределенных смешанных статистик.
Глобальная цель — разложить смешанные статистики графа G в линейную комбинацию независимых друг от друга простых и сложных статистик.
Замечание 1. Далее будет рассматриваться лишь один из векторов смешанных статистик. Однако рассуждения можно провести для каждого вектора из матрицы смешанных статистик.
Замечание 2. В общем смысле все статистики графа представляют собой некоторые функции, которые переводят граф в действительное числовое пространство. В этой работе будет подразумеваться под той или иной статистикой реализация функции на заданном графе.
Пусть у нас есть вектор смешанных статистик m и вектор простых статистик s, такие, что | m | > | s |, принадлежащие соответствующим распределениям. Причем оба вектора состоят из независимых одинаково (стандартно нормально) распределенных случайных величин.
Замечание 3. Статистическая независимость элементов вектора s гарантируется по построению.
В силу статистической независимости элементов векторов, не существует линейного отображения из вектора s в вектор m. Однако обратное утверждать нельзя, поэтому выдвинем следующую гипотезу.
Гипотеза. Существует линейное отображение вектора смешанных статистик в вектор простых статистик.
Иными словами, существует матрица A |sxm|, задающая следующее отображение: Am = s.
Введем следующую лемму.
Лемма 1. Пусть дан набор независимых, одинаково распределенных нормально случайных величин 71,72,... 7п- Случайна я величина £ = а171 + а272 + ... + апуп статистически зависима от каждой из случайных величин 7i, коэффициент для которой ai = 0.
Доказательство
Докажем это утверждение для 71.
В силу теоремы [1] о сохранении нормальности при линейном преобразовании, случайная величина £ будет также иметь нормальное распределение.
Для нормальных величин существует критерий независимости, который можно записать для 7j и £:
E(7*£) - ЕЫЕ(£) = 0.
Распишем этот критерий, воспользовавшись тем фактом, что 7* и 7j являются независимыми для Vi = у:
aiE(72) + O2E(71)E(72) + ... + a«E(7i)E(7n) — E(7i)(aiE(7i) + ... + a„E(7„)) = 0, aiD(7i) = 0.
Таким образом в силу критерия независимости случайных величин, £ статистически зависима от каждого слагаемого, коэффициент при котором не равен нулю.
Лемма 2. Матрица А имеет максимально возможный ранг.
Доказательство
Докажем это от противного — в матрице А есть линейно зависимая строка.
Для простоты дальнейших выкладок пусть есть строка, которая является линейной комбинацией двух других, которые между собой линейно не зависят. Каждой из этих строк соответствуют компоненты вектора s:
£ = kir) + к2(,
< У =
X = Mi + . ..Пп7п.
£, у, £ будут нормальными случайными величинами в силу теоремы о сохранении нормальности при линейном преобразовании [1].
Воспользуемся критерием независимости нормальных случайных величин для £ и у:
п
E(£y) = E((kiy + к2£)у) = kiE(y2) + k2E(£y) = kiE(y2) + k2 £ My,
*=i
П
E(£)E(y) = (kiE(y) + k2E(£))E(y) = (kiE(y) + k2 £MMMCr),
*=i
п
E(£y) - ШЖСг) = ki(E(r2) - (E(y))2) + k2 £ MEh^y) - EMECM
*=i
В силу леммы 1: 6г(Е(7*у) — E(7*)E(y)) = 6*a*D7*. Тогда
E(£y) — E(£)E(y) = kiD(y) + k2 ^>*^7*.
*=i
Поскольку 7* распределены стандартно нормально:
E(£y) — E(£)E(y) = kiD(y) + k2 £ M.
*=i
В силу линейной независимости строк матрицы А, соответствующих у и £, ^2П= °*6 = 0. Тогда критерий преобразуется в следующий вид:
E(£r) — E(£)E(y) = kiD(y) = 0, поскольку ki = 0 11 D(y) > 0.
Таким образом, <^ и ц — зависимые случайные величины, что противоречит условию о статистической независимости компонент вектора s.
На основе данного отображения построим следующие преобразования:
Дополним матрицу A|sxm| до матрицы .А|mxm| Существует бесконечно много способов дополнить матрицу таким образом. Для того чтобы уйти от неоднозначности, нужно наложить дополнительные ограничения, о которых будет сказано далее.
После перехода к преобразованию добавленную часть матрицы A будем называть матрицей D^, а изначальную А^. Кроме того, часть нового вектора S будем называть d.
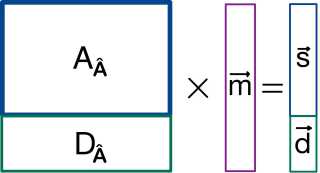
Рис. 4. Построенное линейное преобразование смешанных статистик
В качестве дополнительных ограничений на матрицу D^ примем требование на максимально возможный ранг матрицы D^ и линейную независимость каждой строки матрицы Da от строк матрицы А^. В силу леммы 2, матрица D^ будет ортогональным дополнением матрицы А^.
При линейной независимости строк матрицы А компоненты векторов s и d будут статистически независимы.
Таким образом, получившийся вектор d будет нормальным вектором в силу теоремы о сохранении нормальности при линейном преобразовании [1]. Также каждая его компонента статистически независима от компонент вектора s, а матрица А имеет полный ранг (а потому существует обратное преобразование). Итого получаем, что вектор d есть вектор сложных статистик по определению.
Теорема [Бишук]. Преобразование, описанное выше, соответствует разложению смешанных статистик на простые и сложные.
4. Вычислительный эксперимент
В этом разделе производится проверка предложенного метода и сравнение его с существующими методами на реальных данных.
4.1. Наборы данных
Эксперимент проводился на наборах данных «Сога» [9] и «Citeseer» [10], которые представляют собой информацию о научных статьях и их цитировании.
Cora
Датасет «Сога» [9] — это один из наиболее часто используемых датасетов в задачах классификации и кластеризации графов. Он состоит из 2708 статей, взятых из базы arXiv и разбитых на семь категорий: биология, информатика, право, математика, медицина, физика и социология. Каждая статья представлена в виде узла графа, а связи между статьями — это ссылки между ними.
Каждая статья представлена в виде признаков, являющихся мешком слов (bag-of-words) из 1433 уникальных терминов, которые были извлечены из полного текста статей.
Таким образом, датасет представляет собой ориентированный граф, каждая вершина которого представлена набором из 1433 признаков.
Citeseer
В качестве второго датасета для тестирования предложенного метода был выбран датасет «Citeseer» [10], который традиционно используется для задачи классификации статей по научным темам. Датасет содержит статьи из компьютерных наук и связанных с ними областей, таких как базы данных, информационный поиск и машинное обучение. Каждая статья представляет собой узел в графе, а ссылки на другие статьи формируют ребра. В датасете всего б классов научных тем: базы данных, интеллектуальная обработка информации, машинное обучение, информационный поиск, распределенные системы и робототехника. Он содержит 3327 статьи и 9228 ссылки между ними. Каждая статья представлена в виде метаданных, включающих название, список авторов, перечень ссылок на другие статьи и аннотацию.
Данные датасета были собраны из различных источников, включая базы данных АСМ, DBLP и PubMed. В оригинальной статье, описывающей датасет, авторы провели анализ структуры сети цитирования, выделили основные сообщества статей и оценили качество работы алгоритмов кластеризации и классификации на этих данных.
4.2. Протокол эксперимента
Обучение происходило на популярных датасетах Cora, Citeseer. Для обучения использовалась матрица смежности графов датасета, а также матрица признаков вершин. Кроме того, матрица смежности преобразовывалась согласно алгоритму, предложенному в оригинальной статье GraphVAE [8] и показавшему свою эффективность.
Модель получает на вход матрицу смежности графа, признаки вершин, а также вектор простых статистик, которые вычислялись детерминированными алгоритмами.
На каждой эпохе обучения происходило разбиение графа — выбирались ребра и разбивались на три группы — валидация, обучение и тест. Затем выбирались пары вершин, между которыми ребра отсутствовали, которые также распределялись по этим группам. Процент распределения является параметром обучения, но наиболее стабильные результаты были получены при выделении 15% для теста, 25% для валидации и 65% для обучения.
4.3. Результаты
Для стандартной задачи порождения графов используются критери качества классификации, не требующих порога бинаризации — ROC-AUC и Average Precision. Однако для поставленной задачи необходимо зафиксировать порог бинаризации для подсчета разницы между статистиками поданного на вход и порожденного графов. Для этого происходит проход со всеми возможными порогами для вероятности в матрице смежности порожденного графа и рассчитываем простые статистики. После чего выбирается тот порог, который соответствует минимуму средней абсолютной ошибки между простыми статистиками входного графа и порожденного.
Такой минимум считается лучшим результатом, который может получить алгоритм порождения и записываем его в таблицу результатов.
Таблица!
Результаты вычислительного эксперимента по классификации наличия ребер
|
Dataset |
ROC-AUC |
AP |
MAE (global statistics) |
|
|
GraphVAE |
Cora |
75.18 ± 0.02% |
75.81 ± 0.02 % |
0.066 ± 0.002 |
|
Our method |
76.68 ± 0.02 % |
75.18 ± 0.02 % |
0.046 ± 0.002 ( 30%) |
|
|
GraphVAE |
Citeseer |
82.09 ± 0.01% |
79.94 ± 0.01% |
0.072 ± 0.001 |
|
Our method |
76.28 ± 0.01 % |
76.44 ± 0.01 % |
0.060 ± 0.001 (17%) |
Как видно из табл. 1, предложенный метод порождает графы с статистиками, более близкими к исходным, чем обычная модель GraphVAE.
Предполагается, что уменьшение значения критериев качества реконструкции можно нивелировать, используя другой подход к агрегации простых статистик либо более тон- кой настройкой параметров обучения. Подробнее этот вопрос будет исследован в будущих работах.
5. Заключение
В ходе данной работы был разработан и теоретически обоснован новый метод порождения графов, использующий идею разделения статистик графа на простые (легко вычислимые и интерпретируемые) и сложные. Эксперименты, проведенные на наборах данных Cora и Citesser, показали эффективность предложенного метода в сравнении с оригинальной моделью графового мариационного автокодировщика.
Небольшое снижение критериев качества реконструкции оставляет модель на уровне актуальных моделей оригинальной архитектуры, но при этом позволяет порождать графы с заранее заданными свойствами.
Предложенный подход можно обобщить на прочие модели, преобразующие данные в некоторое скрытое представление. Это может быть полезным, например, при порождении молекулярных структур или сетей связей между людьми.
В будущих работах планируется расширить предложенный метод, используя дополнительно новые простые статистики; исследовать влияние различных простых статистик на ограничение свободы порождения графов; рассмотреть разнообразные методы агрегации графов в векторе одной вершины.
Список литературы Метод порождения графов с контролем статистических свойств
- Боровков А.А. Теория вероятностей. Москва: Наука, Физматлит, 1986. 432 с.
- Pattabiraman В. [et al.\. Fast algorithms for the maximum clique problem on massive sparse graphs // Algorithms and Models for the Web Graph: 10th International Workshop. 2013. P. 156-169.
- Saramaki J. [et al.}. Generalizations of the clustering coefficient to weighted complex networks // Physical Review E. 2007. V. 75(2). P. 027105.
- Ying Z. [et al.}. Gnnexplainer: Generating explanations for graph neural networks // Advances in neural information processing systems. 2019. V. 32.
- Kipf T.N., Welling M. Variational Graph Auto-Encoders // Stat. 2016. V. 1050. P. 21.
- Chamberlain B. [et al.}. Grand: Graph neural diffusion // International Conference on Machine Learning. 2021. P. 1407-1418.
- Latora V., Marchiori M. A measure of centralitv based on network efficiency // New Journal of Physics. 2007. V. 9(6). P. 188.
- Kingma D.P., Welling M. Auto-Encoding Variational Baves // Stat. 2022. V. 1050. P. 10.
- Sen P. [et al.}. Collective classification in network data // Al magazine. 2008. V. 29(3). P. 93.
- Rossi R., Ahmed N. The network data repository with interactive graph analytics and visualization // Proceedings of the AAAI conference on artificial intelligence. 2015. V. 29(1).
- Deng L. The mnist database of handwritten digit images for machine learning research [best of the web] // IEEE signal processing magazine. 2012. V. 29(6). P. 141-142.
- Krizhevsky A. [et al.}. Learning multiple layers of features from tiny images // Technical Report University of Toronto. Toronto, Ontario. 2009.
- Sohn K., Lee H., Yan X. Learning structured output representation using deep conditional generative models // Advances in neural information processing systems. 2015. V. 28.
- Mitton J. [et al.}. A Graph VAE and Graph Transformer Approach to Generating Molecular Graphs // ArXiv, abs/2104.04345.
- Simonovsky M., Komodakis N. Graphvae: Towards generation of small graphs using variational autoencoders // Artificial Neural Networks and Machine I.earning K'AXX 2018: 27th International Conference on Artificial Neural Networks. 2018. P. 412-422.
- Zhao J. [et al.}. GraphTune: An Efficient Dependency-Aware Substrate to Alleviate Irregularity in Concurrent Graph Processing // ACM Transactions on Architecture and Code Optimization. 2023. V. 20(3). P. 1-24.
- De Cao N., Kipf T. An implicit generative model for small molecular graphs // ICML 2018 workshop on Theoretical Foundations and Applications of Deep Generative Models. 2018.
- Velickovic P. [et al.}. Graph attention networks // Stat. 2017. V. 1050(20). P. 10-48550.


