Метод повышения эффективности процедур анализа независимых компонент и обращения свертки при восстановлении формы сигналов по измерению их смеси

Ранее рассмотрены методы разделения смеси сигналов, анализа независимых компонент, а также процедуры, обратной относительно смешивания сигналов, выполненного на основе совместной свертки [1–5]. Проанализированы как алгоритмы реального времени (РВ), так и алгоритмы обучения с формированием обучающей выборки. Большая часть алгоритмов РВ методом простого усреднения может быть преобразована в алгоритмы с обучающей выборкой. Некоторые алгоритмы позволяют извлекать из смеси все компоненты одновременно (параллельно), другие — выделяют первичные сигналы (ПС) смеси один за другим (последовательно).

Эта статья отражает поиск единой концепции, которая позволит объяснить большинство алгоритмов со статистической точки зрения. В ней введен метод оценивающих функций, который объясняет общие структуры в большинстве существующих алгоритмов разделения смеси сигналов (РСС). Для этой цели использована геометрия информации и определены оценивающие функции (ОФ) в полупараметрических статистических моделях, которые включают неизвестные функции как параметры (Цханг, Амари, Сичоки (Zhang, Amari, Cichocki) [6]). Различие в большей части существующих алгоритмов РСС состоит только в выборе оценивающих функций. Ниже в терминах ОФ приведен анализ точности алгоритмов и анализ их устойчивости. Это позволяет конструировать различные адаптивные методы для выбора неизвестных параметров, включенных в ОФ и контролирующие точность и устойчивость. При этом метод Ньютона выводится автоматически с помощью стандартизованных оценивающих функций.

В рамках полупараметрической модели и семейства ОФ будет сформулирована стандартная задача РСС (или задача анализа независимых компонент (АНК)). После этого для задач РСС при линейной смеси и при смеси в форме свертки обсуждается и получает дальнейшее расширение вопрос о сходимости и эффективности оценивания при обучении нейронной сети (НС) методом обучающей выборки и методом м-градиента. На основе структуры типа группы Ли представлены геометрические свойства многообразия КИХ-фильтров и сформулирована задача восстановления сигналов при их взаимном смешивании в форме свертки. Затем анализируется эффективность оценивания при обучении с использованием выборки и использовании м-градиента.

ОЦЕНИВАЮЩИЕ ФУНКЦИИ ДЛЯ МЕТОДА АНАЛИЗА НЕЗАВИСИМЫХ КОМПОНЕНТ

Понятие оценивающей функции удобно ввести на простой модели смешивания сигналов:

x(k) = Hs(k) + ν(k), где H — неизвестная смешивающая матрица; si и sj — независимые компоненты сигнала s(k) (каждая из которых может быть коррелированной по времени); число первичных сигналов (т. е. размерность s(k)) равно n; число детекторов информационно-измерительной системы (ИИС), регистрирующих сигналы смеси, в общем случае равно m, так же как размерность сигнала смеси x. В анализируемой здесь системе РСС принимается, что m = = n, а вектор шума ν пренебрежимо мал. Если матрица W (размерности n × n) является предполагаемой размешивающей матрицей — y(k) = Wx(k) (т. е. y(k) — вектор-сигнал такой, что его компоненты yi(k), i = 1,…,n — независимые случайные ПС), — то при обучении W обновляется по правилу

W ( k + 1) = W ( k ) + η F ( x ( k ), W ( k )),      (1)

где η — скорость обучения (которая может зависеть от k ); F ( x , W ) e R n ^х n ; F ( x , W ) — матрица-функция такая, что W ( k ) сходится к истинному решению. Обычно F зависит от x через y ( k ) = = Wx ( k ) и при этом имеет форму F ( y )^. W , как в случае с м-градиентом [7].

Предложены различные виды F , которые во многих (но не во всех) случаях получены как градиент функции стоимости — градиент критерия, который должен минимизироваться. Функциями стоимости могут быть, например, кумулянты высокого порядка, энтропия, отрицательный логарифм функции правдоподобия. Во многих случаях алгоритмы включают свободные параметры, а иногда свободные функции, которые должны быть адекватно выбраны или определены адаптивно. Поскольку функция плотности вероятности (ФПВ) распределения первичных сигналов, образующих смесь, обычно неизвестна, то нет возможности обойтись без использования таких свободных параметров.

Существуют условия, которым должна удовлетворять функция F для того, чтобы алгоритм сходился к истинному решению. Истинное W должно быть точкой равновесия динамического соотношения (1). Но (1) является стохастическим дифференциальным уравнением, поэтому для математического анализа более удобно использовать его форму с непрерывным временем:

A W( t) = Ц-F[x( t), W( t)].(2)

d t

И поскольку x ( t ) — стохастический процесс, его ожидаемая величина определена соотношением

A W( t) = Ц-E{F[x( t), W( t)]}.(3)

d t

Условием, что истинное решение W определяет равновесие в (3), является соотношение (4)

E{F(x,W)} = 0,(4)

где математическое ожидание E берется по x = Hs .

Функция F ( x , W ), удовлетворяющая (4) для истинной (желаемой) матрицы W и условию E{ F ( x , W ' ) } ^ 0 для ложной матрицы W ' , называется оценивающей функцией. Это определение введено по отношению к полупараметрической статистической модели. Теория оценивающих функций приводит к выводу, что обучение с выборкой (при достаточной ее величине) дает сходимость к истинному решению. Кроме того, преимущество использования полупараметрической модели состоит в том, что для задачи РСС она позволяет не оценивать мешающие параметры, т. е. ФПВ первичных сигналов, образующих смесь.

Полупараметрическая статистическая модель

Задача РСС может быть сформулирована в рамках ее статистической интерпретации. Если фактическая ФПВ сигнала s i равна r i ( s i ) и компоненты s i линейно независимые, то совместная функция плотности вероятности (ФПВ) вектора-сигнала s определяется соотношением

n

r(s) =П r( s). (5) i=1

Вектор наблюдений x является линейной функцией s (т. е. x = Hs и s = H ^-1 x = Wx ), поэтому выражение ФПВ x через W = H ^-1 имеет вид:

p ( x , W , r ) = det | W |· r ( W ^. x ). (6)

Поскольку ФПВ r неизвестна (кроме того, что она удовлетворяет (5)), то модель вероятности (6) для x включает два параметра: W , который требуется оценить, и неизвестный параметр-функцию r = r 1 … r n ("мешающий параметр"), о котором можно пока не заботиться. Такую статистическую модель, включающую (бесконечную) степень свободы в виде функции, можно назвать полупара-метрической. В общем случае оценка W — достаточно трудная задача именно из-за неизвестной функции r . Однако преимущество использования полупараметрической модели состоит в том, что для задачи РСС (включая смеси со сверткой) она позволяет не оценивать мешающие параметры, т. е. ФПВ первичных сигналов, образующих смесь.

Метод получения оценок с помощью анализа полупараметрической статистической модели использует основные понятия концепции информационной геометрии.1) Последующее изложение построено на выводах и следствиях полупарамет- рической статистической модели, концепции информационной геометрии и прямых результатов работ, указанных в приведенной выше ссылке.

Оценивающей функцией является функция (с матричным значением) F ( x , W ) = | F ab ( x , W )| от аргументов x и W , не включающая мешающего параметра r . Эта функция удовлетворяет соотношениям:

• 1)    E W , r { F ( x , W^' )} = 0 при W^'= W , (7)

2)E w r { F ( x , W ' ) * 0 при W ' * W , (8)

где E W , r — символ математического ожидания, определяемого по плотности вероятности (6). Кроме того, накладывается требование, чтобы (7) выполнялось для всех r вида (5). Индексы а , в , с и другие (здесь и далее) представляют компоненты первичного и восстановленного векторов-сигналов, т. е. s и y .

В отдельных случаях вместо 2) необходимо выполнение более мягкого условия, которое состоит в том, чтобы матрица K в (9) не была вырожденной:

f 9 1

• 2)    K = E_W/ j — F ( x , W )k (9) [d W J

Другими словами, условие 2) выполняется только локально. Следует отметить, что K — линейный оператор, отображающий матрицу на матрицу. Компоненты K имеют вид

К = F

K ab , j   ^E W , r

^F F ab ( x , W ) f , .^{5 W}j           J

где W ij — элементы W ; индексы i, j , a , b и др. соответствуют представлению компонент наблюдаемого сигнала x . Удобно использовать индексы А , В ,… для представления пар индексов ( a,b ), ( i , j ) и др. Тогда для А = ( a,b ), В = ( с , i ) K имеет матричное представление K = [ K A B ] , которое действует на ( W B ) = ( W j ) по правилу: KW = = E ^KAB^WB = £ ^Kab , W . Обратный относительно

B i , j

K оператор определяется обратной матрицей K = [ K AB ].

Если имеется оценивающая функция (ОФ) F ( x , W ), то для наблюдаемых данных x (1),…, x ( N ) оценка величины W с использованием этой обучающей выборки определяется уравнением

N

£ F { x ( k ), W } = 0.

k = 1

Оно получено заменой математического ожидания в (7) суммой наблюдаемых величин. Так же как обучающий алгоритм в РВ определен выражением (1), уравнение для оценки по выборке выполняет свою роль без использования неизвестной ПРВ r ("мешающего параметра"). Так что правомерны две задачи:

• 1.    Существует ли оценивающая функция, которая работает без знания r .

• 2.    Каким образом найти "хорошую" ОФ F (в то время как их достаточно много).

Допустимый класс оценивающих функций

Алгоритмы, предложенные Джутен и Хераулт (Jutten, Herault [11]), Беллом и Сейновским (Bell, Sejnowski [12]), Амари (Amari [13]), Кардосо и Лахельдом (Cardoso, Laheld [14]), Ойа и Каруненом (Oja, Kahrunen [15]), использовали различные ОФ, найденные на основе эвристик. Они получались и хорошие, и плохие. ОФ F лучше, чем F ', когда ожидаемая ошибка оценки разделяющей матрицы W ^ˆ , полученная по F , меньше, чем полученная по F '. Но может случиться, что F лучше, чем F ', при условии, что истинное (неизвестное) распределение — r (s ), но F ' лучше, когда это распределение — r ' (s ). Следовательно, вообще говоря они не сравнимы. Семейство (или класс) ОФ считается допустимым, если в этом семействе содержится (и ее можно найти) эквивалентная или лучшая ОФ сравнительно с любой ранее выбранной ОФ. Целесообразно ограничиться рассмотрением допустимого класса ОФ.

Амари и Кардосо (Amari, Cardoso [16]) с использованием геометрической теории информации [17], [18] показано, что множество ОФ в виде

( x , W ) = I - φ ( y ) y ^T

(или в покомпонентной форме)              (11)

F ij ( x , W ) = δ ij - φ i ( y i ) y j )

дает допустимый класс (множество) ОФ, где φ ( y ) = [ φ 1 ( y 1 ), φ 2 ( y 2 ),…, φ n ( y n )]^T включает произвольные нетривиальные функции φ i ( y i ). Можно показать, что это действительно ОФ. Когда W — истинное решение, то y i и y j являются независимыми. Поэтому для любого r выполняется соотношение

^E r , W ^{ 9 i ⁽ y, ) y J ^} = E te ⁽ y i ^)} • ^E{ y J ^} = ⁰ при i * j .

Но, когда W не является истинным решением, это соотношение в общем случае не выполняется. Для диагональных элементов (т. е. при i = j ) E{φ i ( y i ) y i } = 1, и это определяет величину восстановленного сигнала y i . Поскольку амплитуда сигнала может быть произвольной, то можно положить диагональные элементы F ii тоже произвольными (включая элементы типа F ii = 0).

Рассмотрим типичные примеры ОФ. Положим, что q(s) = П- q (si) — неверно определенная ФПВ s, отличающаяся от реальной ФПВ r(s) = П”-i r(si). Отрицательный логарифм функции правдоподобия для x (при ФПВ q(s)) имеет вид

P(x, W) = - det | W - ^ n-1 log q,(y ,), где yi — i-я компонента от Wx (зависящая от x и от W). Критерий минимизации ρ интерпретируется как минимизация энтропии, или максимизация правдоподобия. Положим, что ф, (yi) -

• -    ——log q , ( y , ). Градиент p дает ОФ в виде d y

F ( x , W ) - ^p ( WW - W - T - ф ( у ) x T .

Можно показать, что F — ОФ. Однако, когда F есть ОФ, то F ( y ) = F ( x , W ) W T W = [ I - ф ( у ) y ^T] W также является ОФ. При этом выполняются соотношения: E{ F ( y )} = 0 и {E{ F ( x , W )} = 0.

Для истинного распределения компонент сигнала s в виде ПРВ r лучший выбор φ ( = 1, 2,…, n ) обеспечивает полученное Пхамом (Pham [19]) выражение

d ф , -, log r(s)• ds

Показано также, что F ( x , W ) и F ( y ) связаны линейно и оценивающие их уравнения дают одно и то же решение, поэтому их можно считать эквивалентными ОФ.

В качестве общего случая целесообразно рассмотреть произвольный (обратимый) линейный оператор R ( W ), действующий на матрицах. Когда F ( x , W ) является ОФ-матрицей,

R ( W ) ■ F ( x , W ) также будет ОФ-матрицей, поскольку

E W , _r { R ( W ) ■ F ( x , W )} -

- R ( W )E w , { F ( x , W )} - 0.

Кроме того, F ( x , W ) и R ( W ) ■ F ( x , W ) являются эквивалентными в том смысле, что выведенные оценки в точности одинаковые, т. к. оба уравнения (12) и (13) дают одно и то же решение W , (пренебрегая произвольным масштабированием и изменением порядка компонент сигнала, восстановленного из смеси):

К N F [ x ( k ), W ] - 0,              (12)

k 1

К N _XR( W ) ■ F [ x ( k ), W )] - 0.       (13)

k 1

Это определяет эквивалентный класс ОФ, т. к. при осуществлении оценивания по выборке эти ОФ по существу равноценны.

Однако две эквивалентных ОФ F ( x , W ) и R ( W ) ■ F ( x , W ) дают различные динамические свойства при обучении нейронной сети в РВ, т. е. динамические свойства алгоритмов (14) и (15) для оценки W в РВ полностью различны:

W ( k + 1) = W ( k ) + η F ( x ( k ), W ( k )),              (14)

W ( k + 1) - W ( k ) + n ■ R ( W ( k )) ■ F ( x ( k ), W ( k )). (15)

При этом, чтобы получить хороший алгоритм РВ для получения размешивающей матрицы, необходимо вместо (1) рассматривать расширенную форму ОФ R ( W ) ■ F ( x , W ).

Стандартизованная ОФ и адаптивный алгоритм Ньютона

Динамика обучения в виде

A W ( k ) - W ( k + 1) - W ( k ) - n ■ F [ x ( k ), W ( k )] ■ W ( k ) (16) может быть ускорена на основе использования метода Ньютона, который определяется соотношением

A X ( k ) - n ■ K ^-1 [ W ( k )] ■ F [ x ( k ), W ( k )].

Поскольку K ^-1 F является эквивалентной ОФ относительно F , то видно, что метод Ньютона определяется с помощью ОФ      F * ( x , W ) -

• -    K ^-1( W ) ■ F ( x , W ). Метод Ньютона сходится линейно. Решение, получаемое этим методом, всегда устойчиво, потому что гессиан F ^* является единичной матрицей. Это следует из соотношения

• K • - E J^ F- l - ^ K l E{ F } + K ^-1 о K - 1 .

(d X d X

Стандартизованная ОФ-матрица F ^* описывается выражением

^F * b ^- c ab ^{{ k}b ■ ^ 2 ■ Ф а ⁽ У а ) ' У ь - Ф ь ⁽ У ь ) ' У а ^} , a ^ ^Ь ; ⁽¹⁷⁾

включает параметры σ_a ² и k_a , которые обычно известны [14], [16], [20]. Они зависят от статистических свойств первичного сигнала s a , т. е. от компонент первичного сигнала s , образующего смесь. С параметрами o_a и k b связан параметр c_ab -

------. (Напомним, что а и Ь — буквен- kakb ‘^Хь - 1

ные обозначения индексов, об использовании которых было сказано выше).

Для выполнения метода Ньютона необходимо использовать адаптивный алгоритм, который оценивает параметры. Это не только ускоряет сходимость, но и автоматически обеспечивает устойчивость решения. Если σa2(k) и ka (k) — оценка параметров в дискретный момент времени k, то для обновления параметров может использоваться адаптивное правило вида ka (k + 1) = (1 - П0)ka (k) + ПоФа (Уа (k) ),

^2 (k + 1) = (1 - По К (k) + П 0 У2 (k), где η0 — параметр скорости обучения. При этом в качестве диагонального элемента матрицы F возможно использовать Faa = 1 - y^. Тогда восстановленный сигнал будет нормализован: ст^ = 1, так что F* принимает упрощенный вид:

*

F аЬ

— V^H k b • Ф а ( У а ) • У ь — Ф ь ⁽ У ь ) ' У а ^} , a * ^{Ь . (18)} k_ak_b

Метод адаптивного выбора функции φ

Величина ошибки оценки W зависит от вида F ( x , W ) или F ^*( x , W ), т. е. от функций φ . Хотя стандартизованная ОФ F ^* улучшает устойчивость и сходимость решения, ошибка алгоритма при обучении с использованием выборки и в режиме реального времени зависит от ПРВ φ . Снижение величины ошибки достигается адаптивным методом выбора φ .

Если для получения φ использованы данные фактической ПРВ первичных сигналов, то оцененное значение W ^ˆ является оценкой максимального правдоподобия и оно эффективно в том смысле, что (асимптотическая) ошибка минимальна. Но установить ПРВ сигналов источника трудно, поэтому используется параметрическое семейство ПРВ φ : φ а = φ а ( y ; Θ n ) для каждой компоненты s a сигнала источника (ПС) s , а обновление параметра Θ n осуществляется по соотношению

А 0 = п ^{д Р а 0} 5 0 _а

.

Существует несколько моделей выбора φ а . Смесь гауссианов — один из методов для аппроксимации распределений сигнала. Это — параметрическое семейство

q ⁽ у ; ^{0 )} = Е L v exp i^-

⁽ x ^- А )² I

2^ f

где Θ состоит из численных значений vi,µi и σi2 . Отсюда выводится соответствующая параметри- ческая плотность φ(y;Θ). Такая модель ПРВ включает "надгауссову" (обостренное) и "подгауссову" (сплющенное) плотности распределения. Более простой метод состоит в использовании семейства обобщенных распределений Гаусса: q (у; 0) = = c • exp {-1 y 0}, где 0 — единственный настраиваемый параметр. Это семейство также покрывает надгауссову и подгауссову плотности. Адаптивные нелинейные активационные функции, используемые в алгоритмах анализа независимых компонент, в этом случае имеют вид q (у; 0) =

= <5 • sign( У )| У |⁰ 1 , где ё — положительная константа масштаба.

Другая форма экспоненциального семейства ПРВ предложена Цхангом (Zhang et al. [20]). Она тоже объединяет три вида типовых распределений вероятности (гауссово, надгауссово и подгауссово распределения) и имеет вид q_а ( s , 0 _а ) = = exp { 0 T g ( s ) - ^ ( 0 _а ) } , где 0 _а — канонические параметры, g (s) — адекватная вектор-функция, а ψ ( θ _a ) определяет нормализацию распределения. Плотность вероятности φ а , соответствующую этому распределению, дает выражение

Ф а ⁽ У ) = - Т log q a ⁽ У , ⁰ а ) = ^{0 T} ^ ⁸ ' ⁽ У ^). d y

В [20] предложено использовать также трехмерную модель (вектор распределений): 8 ( У ) = [logseсh( У ), - У 4 , - У ²]^T или g' ( у ) = = [tanh( У ), У 3 , У ]^T. Такой векторной модели соответствуют типичные виды показанных выше плотностей, т. е. модель Цханга также определяет надгауссову, подгауссову и гауссову плотности распределения. При этом ϕ_a ( y ) является их линейной комбинацией, объединяющей все случаи. Параметр θ _a адаптивно определяется по соотношению

0 а ( к + 1) = 0 а ( к ) - П ( к ) • [ g ( У а ( k )) + E{ g ( У а )}] , где E{ g ( y_a )} может также быть оценено адаптивно.

ОЦЕНИВАЮЩИЕ ФУНКЦИИ

В СЛУЧАЕ ШУМА

При анализе случая с наличием шума x = Hs + + ν , где ν — вектор шума при измерении сигналов смеси, полагается, что шум гауссов с некоррелированными компонентами и что его ковариационная матрица R_νν — диагональная:

R vv = E{ vv ^T} = Диаг .{ ст 2 , ст 22 ,..., ст ²}.

Кроме того, чтобы фиксировать масштаб первичных сигналов, образующих смесь, принимается, что Е{ s 2 } = 1.

Размешивающая матрица W = H ^-1 определяет оценку y первичного вектора сигнала s : y = W ^. x .

С учетом принятых условий (и обозначений) справедливо соотношение: y = s + Wv = s + V , где V = Wv — вектор шума, у которого компоненты коррелированные. В случае наличия шума функции типа F = I - φ ( y ) y ^T в общем случае не являются ОФ. Действительно, даже если y выведено из реальной размешивающей матрицы W , то все же ^{E{ I} - Ф ( У ) У T } * 0, ^т. к. y i и y j не являются больше независимыми, даже когда W = H ^-1. Однако даже для случая наличия шума существуют ОФ.

Для истинного значения размешивающей матрицы W = H ^-1 слагаемое с шумом V = Wv имеет (как и ν ) гауссово распределение. Для ковариационной матрицы V преобразованного шума V справедливо соотношение      V = E{ V V T } =

= E{Wvvt Wt} = WRVVWT.

При анализе возможных видов ОФ для условий наличия шума Каванабе и Муратой (Kawanabe, Murata [21]) в качестве наиболее простого варианта найдена функция-матрица F ( y , W ) , элементы ( F ab ) которой определяются выражением

^Fab ( У , ^{W )} = У 3 У ь - ³ • v aa ' У а ' У ь -

- 3 ' vab ' y2 + 3 ' vaa ' vab , где vab — элементы матрицы V. Причем показано, что при W = H-1 выполняется E{F(y, W)} = 0, т. е. найденная функция-матрица F(y, W) является ОФ. Следовательно, адаптивный обучающий алгоритм (19) эффективен даже при значительном гауссовом шуме:

A W ( k ) = W ( k + 1) - W ( k ) =

= П( k ) • F [ y ( k ), W ( k )] • W ( k ).      (19)

Когда ковариационная матрица Rνν шума измерения неизвестна, необходимо произвести ее оценку. С использованием метода факторного анализа Икедой и Тойамой (Ikeda, Toyama [22]) получено адаптивное правило для определения недиагональных элементов матрицы V :

vab(k + 1) = (1 – ηо) vab(k) + ηо ya(k)yb(k), где ηо — параметр скорости обучения.

К сожалению, обучающий алгоритм (19) не всегда обладает устойчивостью. Устойчивость обеспечивается только при использовании стандартизованной ОФ F* , которая реализуется адаптивным методом Ньютона. При этом ОФ F* может быть получена методом, подобным рассмотренному выше случаю без шума.

ОЦЕНИВАЮЩИЕ ФУНКЦИИ

ДЛЯ КОРРЕЛИРОВАННЫХ ПО ВРЕМЕНИ СИГНАЛОВ ИСТОЧНИКА

Независимые сигналы источника смеси (или первичные сигналы (ПС)) во многих случаях бывают коррелированными во времени. Если известен этот факт, процедура РСС становится проще (даже если не известны точные значения временн ы х коэффициентов корреляции). Для алгоритма разделения смеси в таком случае достаточно корреляций второго порядка. Полное представление о методе РСС для описанных условий дает анализ моделей первичных сигналов.

Модель первичных сигналов

Для взаимно независимых ПС источника s i ( i = = 1,…, n ) принимается линейная стохастическая модель:

L i

S ⁽ k ) = £ a_Ts i ⁽ k ^- p ) + S i ⁽ k ),           ⁽²⁰⁾

p = 1

где L i — параметр, определяющий конечный интервал временнóй корреляции i -го ПС;²⁾ ε i — независимые, одинаково распределенные (со средним, равным нулю) элементы временнóго ряда "обновления" ³⁾. Элементы этого ряда могут быт гауссовы или негауссовы. Здесь достаточно принять, что для них выполняются условия:

E{ s , ( k )} = 0; E{ s , ( k ) s/ k ')} = 0 при i * j или k * k .

Введение оператора сдвига z^-1 (такого, что z^-1 s i ( k ) = s i ( k – 1)) преобразует соотношение (20) к виду:

A i ⁽ z^{-1 )]} s i ^{( k} ) = S i ^{( k} ), где A , ⁽ z^-1) = ¹ - y L = 1 a ,p z - ^p .

При использовании обращения полинома Ai ПС представляется в виде si(k) =[Ai-1 (z-1)] • Si(k), где Ai-1 (z-1) = y=0 aip • z-p

Функция A_i ^-1( z ^-1) представляет импульсный отклик, с помощью которого i -й источник ПС s i ( k )

определяется по εi(k) и соответственно набор {si(k)} определяется по сигналам {εi (k)}. При этом если ri (εi) — ПРВ для εi (k), то условная плотность ПРВ si(k) (условная относительно прошлых значений сигнала) представляется в виде p A sA k )l sX k - 1), sX k - 2),...}=

= r i

^s X k ) ^- E a ip s i⁽ k " P ) ^p

> = r { A ⁽ z -1) s X k ) } . (21)

Поэтому для вектора сигналов источников s(k)=[s1(k),…,sn(k)]T в момент (k) условная плотность вероятности определятся соотношением p{s(k) |s(k -1),s(k - 2),...} =

= П г ^{[ AAz ^{-1 )]} s i^{(k )}} .                 (22)

i = 1

Удобно (для краткости) ввести обозначения (23)

£ = ^[ ^ i , ⁸ 2 ,..., 8 n ^] ,

A (z^-1) = Диаг . { A i (z^-1),..., A n (z^-1)}, n                                         (23)

r(£) = n гХ8Д i=1

s(k,пред.) = {s(k -1),s(k -2),...}, а также сокращения в форме (24) там, где это не будет затруднять их понимание:

^s k = ^{s ( k} ), x k = ^{x ( k} ),     У k = У ^{( k} ) = ^{W ( k ).     (24)}

При этом соотношение (22) принимает вид p{s(k) |s(k,пред.)} = r{A(z-1)s(k)}.

Совместная плотность вероятности набора { s (1), s (2),..., s ( N )} представляется в форме:

p ( s (1), s (2),..., s ( N ) ) =

NN

= П p { s ( k )| s ( k , пред .)} = П r { A (z^-1) s ( k )}, (25) k = 1                                       k = 1

где при k <  0 полагаем s ( k )равным нулю. (Практически при k <  0 s ( k ) не равно нулю, так что (25) является приближением, которое выполняется асимптотически, т. е. для больших значений N ).

Модели источника (ПС) определяются n функциями r ( ε ) и n функциями, обратными относительно функций импульсного отклика A (z^-1). Процедура РСС извлекает независимые сигналы из их мгновенной линейной смеси x ( k ) без знания точной формы r ( ε ) и A (z^-1). Можно сказать, что r ( ε ) и A (z^-1) следует трактовать как неизвестные и мешающие параметры.

Для данных N наблюдений смеси { x (1), x (2),…

…, x ( N )} их совместная плотность распределения получается из (25) и соотношений s k = Wx k , где W = H ^-1. Эта совместная плотность имеет вид (26) и определяется размешивающим матричным параметром W = H ^-1 и мешающими параметрами A и ПРВ { r } =1,…, N модели источника сигналов:

p { X 1 ,..., x N , W ; A , r } =

N

= Det | W | N П r k { A (z^-1) Wx k }.      (26)

k = 1

Оценки максимального правдоподобия

Если представить (на момент), что r и A известны, то для того, чтобы оценить W , будет возможно использовать метод максимального правдоподобия (МП). Логарифм МП, полученный на основе (26), имеет вид:

p ^{( N} ) ( X 1 ,..., x N ; W , A , r ) =

=- log p { X 1 ,..., x N ; W , A , r } =

= - N • log| W |-]T log r {A(z-1) Wxk} = k=1

= - N • log| W | -]T log r { A (z^-1) y _k },       (27)

k = 1

где y _k = Wx _k . Оценка МП W максимизирует приведенную выше функцию правдоподобия при данных N наблюдений x ₁ ,..., x _N .

Полагая p ( y _k , W ) = - log r { A (z^-1 ) y _k }, можно видеть, что ρ зависит не только от y k , но (из-за оператора A (z^-1) ) зависит также от прошлых значений y k– 1 , y k– 2 ,… Кроме того, ρ функционально зависит от W только посредством набора y k . Это позволяет представить ρ ^{( N )} в виде

p ^{( N} ) =- N • log| W | -]T p ( y _k , W ).

k = 1

Малое изменение dρ, связанное с малым изменением W (от W до W + dW), определяется выражением dp = -Фг (Ay k )T d(Ay k),           (28)

d где фг (y) =--log r(y)— вектор. Теперь, по- dy скольку d(Ayk) = A dyk и dyk = dWxk = dXyk, то справедливо соотношение dρ = φr(Ayk)TA dXyk . А это приводит к скорости функции МП на единицу изменения dX:

^P X- =^б< ^W = i^{[ I} "( Ф г ^{( A}y - ^{) A }} yT ^] ,     ⁽²⁹⁾

где ϕ_r A — вектор-столбец с компонентами φ j A j (z^-1).

Далее, поскольку d ρ в компонентной форме — dp — Е c j dX „ , то dp] dX — матрица с элементами c ij . Следовательно, φ r ( Ay ) Ay ^T в компонентах представляется в виде φ i ( A i (z^-1) y i )^. A i (z^-1) y j .

d p

Если положить    — — F(y, W; r, A) — I - dX

- { ф_г ( Ay ) • A } y T , то уравнение правдоподобия (с учетом сокращений (24)) приобретает форму

N

Е F ( y k ,W; r ,A ) = 0 ,              (30)

k = 1

а решение W ^ˆ уравнения (30) дает оценку максимального правдоподобия размешивающей матрицы.

Оценивающие функции

Поскольку ПРВ сигналов источника { r i } и фильтры { A i (z^-1)}неизвестны, нет практической возможности использовать рассмотренные выше оценивающие функции F , которые зависят от r и A . Поэтому целесообразно выполнить поиск ОФ в классе функций вида

F ( y,W , q ,B ) = d ^ yLW q B ) =

• = I - ф_д {( B (z^-1) y ) • B (z^-1)} • y ^T,           (31)

где q — любое (фиксированное) независимое распределение; матрица B(z-1) = Диаг.{B1(z-1),…, Bn(z-1)} Li с фиксированными фильтрами Bi (z-1) — Е bp z-p .

p = 0

Это — оценивающая функция (при любых q и B ), т. к. она удовлетворяет соотношению E w , r , A [ F ( y,W , q , B )] = 0 для любых сигналов источника, имеющих независимые распределения компонент, и фильтров A (z^-1). Когда истинный мешающий параметр r = q и A = B (z^-1), то F ( y, W , q , B ) является функцией МП. Однако даже если q и B определены неверно, это соотношение может служить в качестве ОФ.

Условия, определяющие возможность идентификации

Более последовательно и корректно условия возможности идентификации W установлены Тонгом (Tong et al. [23]) и Комоном (Common [24]). Должно выполняться (по крайней мере) одно из двух условий:

• 1.    Все независимые сигналы — источники сме-

• си имеют различные спектры, т. е. передаточные функции Ai(z-1) различны.

• 2.    Когда некоторые сигналы имеют одинаковые спектры, распределения r i этих сигналов — негауссовы, кроме одного сигнала.

В целом эти условия порождают общую формулировку: когда удовлетворяются условия, определяющие возможность идентификации, минимальный допустимый класс оценивающих функций является линейной комбинацией недиагональных элементов матрицы F ( y, W , q , B ) , в которой q и B произвольные. Оценивающее уравне-

E N

F ( y _k ,W , q ,B ) = 0 .

k 1

Адаптивный обучающий алгоритм на основе такой ОФ принимает вид (32), а в более общем случае при использовании стандартизованной ОФ принимает вид (33):

A W ( k ) — n( k ) F [ y ( k ), W ( k ) ] • W ( k ),        (32)

A W ( k ) — n ( k ) F * [ y ( k ), W ( k )].              (33)

Стандартизованная оценивающая функция и метод Ньютона

Если взять обратимый (т. е. не сингулярный) матричный оператор R ( W ) — ( R AB ), который может зависеть от W , тогда F и F — R • F — эквивалентные оценивающие функции (ОФ). Одна ОФ F * из класса эквивалентных функций, которая удовлетворяет условию

5F * K — E ( — I d X

— единичный оператор (оператор тождественности), называется стандартизованной ОФ [25]. При этом если задана ОФ F, то ее стандартизованная форма определяется выражением

I SF 1

F* — K "1F , где K — E j^

(d X

Теперь можно вычислить

(d F ( y , W , q , B ) 1

K — E Ar

Id при истинном решении W — H-1. Переписывая F — dp!dX (или dp — -tr(dX) +[ф(;У)t B(z-1)]dXy в компонентной форме, где положено y — [ B(z-1)]y), можно вычислить дифференциал второго порядка, который представляется в виде выражения:

г

л d2 p—d Е Фi(yi)bpyj(k - p) dX-j-—

V i , j , p

у

= E Ф( yi ) Mm (k - P) " biqyj (k - P )dXm dXj + i, j,m,q,k

⁺ E ф^ y- ) Mm ^{( k} - P ^)dXjm M ,          (34)

i, j,m,k где ф\(y) = d^-(y)/dy.

Для истинного решения получается соотношение

E {ф' (yi )yjym } = E {ф(yi )yj } = 0, если не выполняется i = j = m, и d2 p =

= EE{ф i(yr)У2}1 d X 1 +EE{ф(yi)y }dXjdXji + i                                                                         i,j

+ E ^E 1 ^{ф (} y i ) [ E b p y j ⁽ k - p ^{)] 2} i * j    l           P = 0

Г (dX j ) 2 .

Следовательно, квадратичная (относительно набора d X ij ) форма d ρ ² распадается на диагональные члены E,( m i + 1)(d X „ )² и на матрицы более низкого порядка (2 × 2), состоящие из d X ij и d X_ji

(i * j): E {кМ (dXj)2+dXjdXji}. В этихмат-i * j рицах использованы обозначения:

m, =^ ^{ф (} y i ) y 2} ; k i = ^E { ф , ⁽ y i ) } ;

⁵ 2 = ^E 1

E b ip y j ^{( k -} p )    > .

. p = 0                   j

Если положить Fi (y) = 1 - yi2, то восстановленные сигналы удовлетворяют условию E{yi2} = 1. В этом случае диагональные члены равны 2E,dXi2, а диагональные члены (2 х 2)-матриц равны к^г2 (dXij )2 + hidXjdXji, где j^i= E {ф(yi)yi}.

Из проведенного анализа получается условие устойчивости алгоритма: A W = n F ( y , W ) W .

Таким образом, решение для разделяющей матрицы W асимптотически (т. е. для большой выборки сигналов смеси) устойчиво только при условии: T m + 1 >  0, k c >  0, к т к,<г ²с г ² > 1 .

i           i      ijijji

Обратная матрица K-1 имеет ту же структуру, что и K . Ее диагональная часть KAA при A = (i, i) равна k.. .. = —1—, а ее (2 х 2)-диагональная 11, ii 1 + 7mi часть KaA для A = (i,j) и A' = (j',i) равна:

^KAA ' = C j

k/7 2-

- 1

- 1

k i ⁵ j J

где c j =

^. k c y ^ >, 5 c j, - ¹

Кроме того, элементы стандартизованной матрицы-функции F * ( y , W ) определяются в виде

F ‘ = C j [ - k,<7² ф ( y i ) y⁽ j i ) + ф j ( y j ) y i ^j ) ];

^Fj = "^17 ^{{1 -} ф ^{( y}i ) ^yi ^} , ^г д ^{е y}j ) = B i ⁽ z ^{- 1}) y j .

m, + 1

Соответствующий алгоритм обучения, использующий метод Ньютона, определяется соотношением

A W = n - F * ( y , W ).             (35)

ПОЛУПАРАМЕТРИЧЕСКИЕ МОДЕЛИ МНОГОКАНАЛЬНОГО РСС ДЛЯ СВЕРТКИ ПС

В работах [4], [5] развит анализ моделей, алгоритмов и нейросетевых структур, решающих задачу РСС для линейного смешивания ПС. Задача РСС для смесей ПС со сверткой значительно сложнее, и попытки ее решения наметились только после использования нового подхода на основе модернизированной формы градиента [7]. Развитие более совершенного метода РСС (на основе обращения операции многоканальной свертки (ООМС)) связано с появлением элементов теории геометрических структур на многообразиях фильтров [Цханг, Сичоки, Амари [26]).

Геометрические свойства многообразия КИХ-фильтров, основанные на структуре группы Ли, позволяют формулировать задачу РСС при многоканальной свертке ПС в рамках полупараметриче-ской модели, что позволяет вывести семейство ОФ для разделения сигналов из их многоканальной свертки. При этом полезен анализ эффективности приближенной оценки W (z) по выборке на основе использования ОФ. Кроме того, в [20] и [26] показано, что при определенных условиях (отсутствия так называемой сингулярности W 0 ) обучение алгоритма как по выборке, так и на основе м-гра-диента обладает высокой эффективностью.

Элементы формализации задачи и обозначений

В качестве модели смешивания ПС в форме многоканальной свертки рассматривается линейная инвариантная по времени система (ЛИВС):

^{x ( k} ) = E”_P = 0 H p ^{s ( k -} p ),             ⁽³⁶⁾

где H p — ( n × n )-матрица смешивающих коэффициентов при временнóй задержке p (называемая импульсным откликом на время p ); s ( k ) = = [ s 1 ( k ), s 2 ( k ),…, s n ( k )]^T — n -мерный вектор сигналов источника (с нулевым средним и идентично распределенными компонентами); x ( k ) = = [ x 1 ( k ), x 2 ( k ),…, x n ( k )]^T — n -мерный вектор сигналов сенсоров ИИС. Для простоты будет использоваться обозначение ^{H (z)} = 2 ;= 0 ^H p ^z - ^p , где ^z — переменная z-преобразования. H (z) может быть названо смешивающим фильтром. В задаче РСС для ПС в форме многоканальной свертки смешивающий фильтр неизвестен, а целью задачи является восстановление сигналов источника (ПС) с использованием только сигналов сенсоров x ( k ) и некоторой информации относительно распределений ПС.

ООМС для реализации РСС осуществляется с помощью другой (отличной от (36)) ЛИВС общего вида, т. е. "неказуальной" системы:

y( k)=2;=-„ Wp x( k - p ), где y(k) = [y1(k), y2(k),…, yn(k)]T — n-мерный вектор выхода; Wp — (n × n)-мерная матрица коэффициентов (при временнóй задержке p), компоненты которой являются параметрами, определяемыми в процессе обучения соответствующего алгоритма.

Матричная передаточная функция размешивающих фильтров представляется в виде

w (z) = 2 ;=-

W _P • z - ^P .

Цель ООМС состоит в получении выходных сигналов y ( k ) размешивающей модели максимально взаимно ("пространственно") независимыми и c независимыми, но одинаковыми распределениями по времени. Для этого используется полупарамет-рическая модель, c помощью нее создается семейство ОФ, после чего строятся эффективные обучающие алгоритмы для определения параметров разделяющего фильтра W (z).

На практике ООМС выполняется с использованием КИХ-фильтра, т. е. фильтра с конечной импульсной передаточной функцией: W ( z ) =

= 2 L = __o W _p • z ^P , где L — максимальный порядок

(длина) разделяющего фильтра в ООМС. Альтернативно, можно использовать неказуальной фильтр симметричной формы W ( z ) =

Z L /2

p =- L /2

W _P • z ^{- P} .

Геометрические структуры многообразия КИХ-фильтров

При создании обучающего алгоритма использование оптимизации функции стоимости на осно- ве м-градиента эффективно лишь для задачи итеративной оценки параметров. Для случая оптимизации функции стоимости, включающей КИХ-фильтр как целое (т. е. весь набор его параметров), метод м-градиента не оптимален. Поэтому при создании эффективных обучающих алгоритмов для получения оценки параметров размешивающего фильтра полезно рассмотреть подход на основе геометрических свойств многообразия КИХ-фильтров.

Множество M ( L ) всех КИХ-фильтров W (z) длины L (с ограничением, что матрица W 0 обратима)

M (L) = {W(z) I W(z) = 2 L=0 Wp z-P , det(W * 0} имеет размерность n2(L + 1). В общем случае умножение двух фильтров в M(L) приводит к увеличению длины у результирующего фильтра. Поэтому, чтобы использовать возможные геометрические структуры в M(L) , которые приведут к эффективным обучающим алгоритмам для W(z), следует определить алгебраические операции фильтров по концепции операций в группе Ли.4)

Использование м-градиента для РСС с операцией, обратной многоканальной свертке (ООМС)

Группа Ли имеет важное свойство — она допускает инвариантную метрику. С использованием структуры группы Ли можно получить м-градиент функции стоимости ρ(W(z)), определенной на многообразии M(L) :

V P ( W (z)) = ^ W z)) ® W (z) = V p ( W (z)) ® W (z), d X (z)

где d X (z)— переменная, определенная соотноше-нием:⁵⁾

d X (z) = d W (z) ® W ^J (z) = [d W (z) W -' (z)j _L .    (37)

dFp лен соотношением —— = dX q

^d F p , у

(d X,

Для любой матрицы

8 F„             d F_p   „

—— P имеет вид —— P = > dXq           dX q   ^

.

^q , ^{ij у} n X n X n X n

Fp e Rn X n dFpP

*lk ^{d X} _g „ lk .

операция

Поэтому

Альтернативно м-градиент может быть выражен в виде

dF(y, X(z)) производная              является оператором, dX(z)

отображающим M ( L ) на M ( L ) , который пред-

ставляется в виде соотношения

V p ( W (z)) = V p ( W (z)) ® W T (z^-1) ® W (z).

Однако оценивать м-градиент значительно легче при введении (неголономной) дифференциальной переменной dX(z), определенной приведенным a            a n           dp(W(z))   „ выше соотношением. Вычисление          мо- dX(z)

жет быть выполнено двумя способами:

1. Оценить его по соотношению dP(W(z)) = dp(W(z)) 0 WT(z.1) dX(z)     dW(z)          Л

5 F ( y . X (z)) P (z) = y L y L ^FL P z-p 5 X (z)           ^L p " ^{0 L} q ' ⁰ 3 X q¹’     ^,

2. Непосредственно вычислить его с использованием свойства d y ( k ) = d W (z) x ( k ) = d X (z) y ( k ). Из этого выражения видно, что дифференциал d X (z) определяет изменения, которые переносятся каналом РСС на сигнал выхода y ( k ). Это свойство является основным фактором, влияющим на вывод обучающихся алгоритмов для модели разделения сигналов при ООМС.

Принимая, что d X (z) = ^ L =_o d X _p z ^- p e M (L ) и что d X (z)— функция стоимости, определенная на

для любого фильтра P (z) e M ( L ).

На основе элементов проведенного выше анализа осуществлено построение обучающихся по м-градиенту алгоритмов для ООМС . Для выполнения адаптивного обучения в РВ использована функция стоимости в виде

J ( y , W (z)) = E{ p ( y , W (z))} =

= - log | det(W0) | -^ ”=1 E{ log q(y,)}, где q(yi) — оценка для реальной функции ПРВ сигналов источника.

Оценка полного дифференциала d ρ ( y , W (z)) имеет вид

d p ( y , W (z)) =

= d ( ^- log | ^{det( W} 0 ) | - ^ ⁿ ₌ 1 log q ⁽ y , ) ) =

= - tr(d W 0 W o ¹) + ф ^T( y )( y )^Td y ,             (39)

M ( L ) , можно выразить

d p ( X (z)) ^{d X} p

( a p( X (z)) . d X p ,ij

\

V n X n

Из этого следует, что

d p ( X (z)) = _y l d X (z)    ^ ^p = 0

dp(X(z))  p z.

^{d X} p

Оценивающая функция для ООМС обозначена, как F ⁽ y , ^{X (z))} = ^ L _{- 0} F p ⁽ y , ^{X (z))z} - ^p , где F p _e r n ^x n , p = 0,1,2,..., l — матричные функции на

dFD

M(L) . При задании p и q производная p явля-X q ется четырехмерным тензором, который опреде-

5) Эту переменную называют неголономной — обеспечивающей дополнительную связь.

где tr — след матрицы, φ ( y ) — вектор нелинейных активационных функций с компонентами φ i ( y i )

dlog q_i ( y_i )       q_i ^' ( y_i )

—--—--

.

d y_i           q_i ( y_i )

Введение неголономной дифференциальной связи по типу (37) позволяет преобразовать (39) к выражению, имеющему форму d ρ ( y , W (z)) = = -tr (d X 0 ) + φ ^T( y )^.d W (z)^. W ^-1(z)^. y . При этом как следствие получается соотношение, определяющее компоненты м-градиента:

d p ( y , W (z))    _ _T                X

X     = -§0 pI + Фт (y)yT (k - p), dX p p = 1,2,..., L.

После этого с использованием метода (м-) градиентного спуска получается эффективный обучающийся алгоритм в РВ, имеющий вид

^{A W} p ( k ) =- , ( k ) £ ' = 0 MBW p - q ( ^k ) =

= n ( k ) Z q = « № q I - Ф ( У ( k )) y ^T( k - q )] W p - q ( k )   (41)

для p = 1,2,...,L, где η — параметр скорости обучения. В частности, обучающийся алгоритм для W0 имеет выражение

A W ₀ ( k ) = n ( k )[ I - ф ( у ( k )) y ^T ( k ) ] W o ( k ). (42)

Альтернативно может быть использован адаптивный алгоритм с обучением его на выборке измерительных сигналов смеси, т. е. сигналов с сенсоров ИИС:

A W p ( k ) = n ( k ) Z q = 1 S q I - R ‘ k y ) ( q )] W p _ q ( k ),    (43)

где ^R ^^ ⁽ q ) = ^{(1 -} n o ^{) R} * ,y ⁽ q ) + n о Ф ⁽ у ^{( k} )) y ^{T ( k -} q )•

Алгоритмы на основе м-градиента (41) и (43) обладают свойством получать решение для размешивающей матрицы W с примерно равной скоростью для ее компонент. Упомянутым свойством обладают алгоритмы, динамическое поведение которых зависит от общей передаточной функции (ПФ) G ( z ) = W ( z ) ® H ( z ), а не от ПФ смешивающего фильтра H (z). Фактически, обучающийся алгоритм (41) обладает этим свойством в смысле группы Ли. Так, если написать (первую часть) (41) по правилам группы Ли и умножить обе части этого соотношения на смешивающий фильтр H (z) (по правилам группы Ли), то будет получено выражение

A G (z) = - п

d p ( W (z)) d X (z)

® G (z),

где G (z) = W (z) ® H (z).

Поскольку из (40) видна формальная независи- dp(y,W(z)) dX p

мость

от смешивающего канала H(z), то динамические свойства алгоритма (44) зависят от G(z), а сам алгоритм обладает тем же свойством, как у алгоритмов (41) и (43).

Другое важное свойство алгоритма (42) состоит в том, что он поддерживает обратимость матрицы W 0 , если начальное значение W 0 обратимо [27].

ОЦЕНИВАЮЩИЕ ФУНКЦИИ

И СТАНДАРТИЗОВАННЫЕ ОЦЕНИВАЮЩИЕ ФУНКЦИИ ДЛЯ РСС НА ОСНОВЕ ООМС

Наиболее выигрышной является ОФ, которая представлена соотношением

F(x(k), W(z)) = ZL=0 Ф(у(k)) y(k - p)Tz-p -1, (45) где y(k) = ZL_0 Wpx(k - p); ф — вектор данной активационной функции; соблюдается условие, что оператор производной K (z) = с fSF(x, W(z)) 1 Л                          ,

= E1---------- 1 обратим. ОФ является эффек-

[ a x (z)

тивной, когда дополнительно к этому выполняется соотношение F ii ( y i ) = φ i ( y i ) y i -1 [26], [27].

_{п                            с} fd F ( x , W (z)) 1

Оператор производной K ( z ) = E<— --- —

[ d X (z)

это фильтр тензорного типа. Он может быть представлен в форме K (z) = Z L = 0 K p ^z " p , ^где

K p,j,im = Б{ ф '( y(k ))( 5 J ( k - p)}5_n5 jm + 5_т5, S o _p .

Кроме того, при выполнении условия ki ^ 0, klkjo^2 о2 -1 ^ 0, mi +1 ^ 0     производная оператора K(z) обратима. В последнем условии использованы обозначения, введенные Цхангом:

m = ^E{ У 2 Ф' ‘ ⁽У. ^)} , ^ki = ^Е ШУ ^)} , ° " = ^E{ У 2 ^} . ⁽⁴⁶⁾

C j = [ k . k j O .² ° _v ² - 1] - ¹,     l = E{ ^ ( y . )}.          (47)

Метод, основанный на полупараметрической модели, для получения оценки параметров (z-преобразования) размешивающей матрицы, использу-

E N

F ( x ( k ), W (z)) = 0. При дос- k 1

таточно большом значении N оценка W(z,k) сходится к фактическому размешивающему фильтру, причем для этого не требуется знания ПРВ сигналов источника r(s). ОФ не является единственной, т. к. для любого обратимого оператора R (z) (отображающего M(L) на M(L) ) R (z)F(x,W(z)) — также ОФ. При этом, как было установлено, две ОФ эквивалентны в том смысле, что выведенные из них оценки размешивающей матрицы по алгоритму с обучающей выборкой совершенно одинаковы. Однако анализ алгоритма РВ показывает, что динамика обучения различается и, следовательно, целесообразно вводить ОФ, которая обеспечит более эффективный и устойчивый обучаемый алгоритм. Для этой цели вводится концепция стандартизованной ОФ. ОФ называется стандартизованной, если оператор производной c fSF(x, W(z)) 1

K ( z ) = E <----------> является единичным опе-

[ a x (z)

ратором. Далее, если оператор K (z) обратим, то для любой ОФ F ( x , W (z)) преобразование оператором K ^-1(z) , т. е. K ^-1(z) F ( x , W (z)) , является стандартизованной ОФ.

Кроме того, при эффективной ОФ в форме (45) соответствующее выражение стандартизованной ОФ имеет вид

F * ( x , W (z)) = £ L ==0 F * ( x , W (z))z - ^p ,         (48)

где

Fи =        { ф .⁽ y, ) y, - 1 } для i = l, ² ,-, n ;

’     m i + 1

FU = c j { k j °ф .⁽ y ) y, - Ф j ⁽ y j ) y . }    для i * j ;

^FP , j = Ф .⁽ y. ) y j ⁽ k - P WM 2 ) для P ^{- 1.}

Использование стандартизованной формы ОФ имеет определенные преимущества при получении алгоритма с обучением в РВ для оценки размешивающей матрицы. Алгоритм обучения на основе использования м-градиента определяется соотношением

A W (z) = - n - F * ( x , W (z)) ® W (z).    (49)

Этот алгоритм обучения при выполнении условия (47) приводит к устойчивому равновесию, которое обеспечивает получение правильного решения для размешивающей матрицы W (z) = H ^J (z). Для выполнения обучающего алгоритма (49) требуется в РВ оценивать статистики (46) и (47). В частности, если ПС бинарные (принимающие значения 1, -1), то вычисление таких статистик для стандартизованной ОФ достаточно просто. Если принять в качестве активационной функции кубическую функцию p i ( y i ) = y 3 , то статистики оцениваются по соотношениям: m i = 3, k = 3, a i ² = 1, Y j = c i - ¹ = 8. Поэтому стандартизованные ОФ могут быть получены в явном виде.

Повышение эффективности при использовании оценок с обучающей выборкой

Показано, что мгновенная замена V ij ( N ) ковариационной матрицы E{ y i y j } ( i Ф j ) при больших значениях выборки ПС убывает со скоростью 1/ N ². Это свойство называется повышением эффективности при соответствующем оценивании. Цхангом [6], [26] показано, что это свойство сохраняет справедливость при РСС с операцией, обратной относительно многоканальной свертки ПС.

Положим, что F ^* ( x , W ( z )) — это стандартизованная оценивающая функция

E {AXn (z, k) ® AXN (z, k) = N G (z) + O где G*(z) = K-1(z)G(z)K"T(z) =

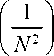
= E { F * ( x , W (z)) ® F * ^T ( x , W (z)) } .

Тогда коэффициенты G ^* (z) выражаются соотношениями:

^G * , .i , ji = c i c a ^ i ° 2 ° l ^k2 к ^lj для i * j , j * ^1,1 * i ;

G 0 * . j. =        C ji k . ° j ² / j E ^{ s . ²p .⁽ s . ^)}     для i * j ;

,       m i + 1

l l j

G p,.i,ji =tt        для p - 1, i , ^J = ^1,2, ... ^, n .

^{, ,} k k j

Используя для F ^* ( x , W (z)) соотношение (48), путем прямых вычислений может быть получен результат, который формулируется следующим образом. Оценка по выборке является эффективной при выполнении условия l = E{ φ ( s )} = 0 для = 1, 2, …, n .

Из результатов анализа, проведенного в этом и двух предшествующих разделах, следует, что для повышения эффективности при оценке по выборке и по алгоритму на основе м-градиента требуется выполнение одного и того же условия: l = = E{ φ ( s )} = 0 для = 1, 2, …, n . Но поскольку в качестве активационной функции нейронных сетей, с помощью которых реализуются алгоритмы, применяются кубическая функция или гиперболический тангенс, то обе эти функции удовлетворяют требуемому условию.

ЗАКЛЮЧЕНИЕ

Рассмотрены оценивающие функции и метод полупараметрической модели для разделения сигналов смеси (РСС), когда смесь реализована в форме многоканальной свертки первичных сигналов (сигналов источника). Для метода определения размешивающей матрицы W (обратной относительно H — матрицы, смешивающей ПС) проанализирована сходимость и условия, обеспечивающие повышение эффективности оценок W как при использовании алгоритма, обучаемого по выборке, так и алгоритма РВ на основе м-градиента.

На первом этапе задача РСС при смеси в форме многоканальной свертки ПС сформулирована в рамках концепции полупараметрической модели, семейства оценивающих функций и стандартизованных оценивающих функций. Преимущество метода, основанного на полупараметрической модели, состоит в том, что в задаче РСС она избавляет от оценки мешающих параметров, т. е. от плотностей вероятности распределения сигналов источника. Из анализа теории оценивающих функций следует, что оценки размешивающей матрицы алгоритмом, обучаемым по выборке (если объ- ем ее достаточно велик), сходятся к реальному решению. При этом, если удовлетворены условия устойчивости, то обучение алгоритма на основе м-градиента также приводит к сходимости к реальному решению независимо от плотности распределения первичных сигналов. Повышение эффективности обоих алгоритмов обеспечивается при выполнении определенных локальных условий.

В статье рассмотрены основные элементы двух математических концепций, использованных для целесообразной формы описания действий на многообразии матричных передаточных функций (МПФ) и на многообразии КИХ-фильтров. Это — операции МПФ на группе Ли и геометрические структуры многообразия КИХ-фильтров.

Идея, концепция и метод использования полу-параметрической статистической модели, а также семейства оценивающих функций разработаны Цхангом, Амари, Сичоки [6], [26], Дугласом [8], Нагаоки [10], Пхамом [18], Каванабе, Муратой [21], Икеда, Тойамой [22], Тонгом [23].