Метод повышения точности определения частотных характеристик технических объектов

Определение основных показателей технических объектов и систем путем анализа частотных характеристик позволяет не только определить режимы надежного функционирования этих систем, но и использовать полученную информацию для модернизации существующих объектов и для дальнейшего проектирования более совершенных объектов.

Методы и алгоритмы теории автоматического управления позволяют получать искомые показатели по информации о входном и выходном сигналах исследуемого объекта. При проведении экспериментов с реальными техническими объектами значения входного и выходного сигналов регистрируются аналого-цифровыми преобразователями (АЦП). В отличие от данных, полученных при моделировании исследуемой системы в ускоренном масштабе времени, реальные экспериментальные данные не только регистрируются в реальном масштабе времени, но и содержат как полезный сигнал, так и случайные составляющие, в ряде случаев значительно искажающие полезный сигнал. В связи с этим необходимо рассмотреть основные особенности получения частотных характеристик реальных технических объектов и систем.

Описание метода

Получение частотных характеристик осуществляется путём подачи на вход исследуемой системы сформированного генератором гармонического сигнала U с последующим проведением гармонического анализа входа X и выхода Y исследуемого объекта:

U ( t ) = U m sin ( to t + V U ) , (1)

X ( t ) = X m sin ( ^ю t + V x ) , (2)

Y ( t ) = Y m sin ( to t + V y ) , (3) где ω – частота генератора; U_M , ψ _U – амплитуда и смещение фазы генератора; X_M , ψ _X – амплитуда и смещение фазы входного сигнала объекта; Y_M , ψ _Y – амплитуда и смещение фазы выходного сигнала объекта.2

Гармонический сигнал U ( t ) формируется генератором, построенным с применением цифроаналогового преобразователя (ЦАП) и позволяющим на основе табличных значений функции синуса с использованием питающего напряжения реализовать функциональную зависимость (1) для требуемых значений амплитуды, частоты и смещения фазы.

Сигналы X ( t ) и Y ( t ) регистрируются АЦП в виде набора дискретных значений, каждое из которых соответствует текущей фазе генератора.

Тогда для входного (2) и выходного (3) сигналов путём Фурье-анализа [1] рассчитываются синфазные и квадратурные составляющие сигналов:

Re X = j X ( t ) cos ( to t ) dt =

T

N X j - i cos

= 1---- j=1

( ( j - 1 ) to A t ) + X j cos ( j to A t )

-A t ,

Im X = j X ( t ) sin ( to t ) dt =

T

1 X j _{- 1} sin ( ( j - 1 ) to A t ) + X j sin ( j to A t )

j = 1

-A t ,

Re Y = j Y ( t ) cos ( to t ) dt =

T

_ N Y j - 1 cos ( ( j - 1 ) to A t ) + Y j cos ( j to A t )

L^L ,

^         2

j = 1                       ²

Im Y = j Y ( t ) sin ( to t ) dt =

T

= 1 Y j - 1 sin ( ( j - 1 ) to A t ) + Y j sin ( j to A t )

j = 1

-A t ,

где T – время интегрирования; N – число значений сигналов за время интегрирования; A t - шаг ин-

тегрирования.

Построение логарифмической амплитудной и частотной характеристик осуществляется по значениям модуля и аргумента для исследуемых частот, которые определяются по следующим выражениям:

Рассмотрим результаты применения формул с (4) по (7) к получаемым сигналам без использования и с использованием дополнительных расчётов. Для получения результатов проведём эксперимент с техническим объектом, схема исследования которого представлена на рис. 1.

С целью упрощения расчётов выберем значения сопротивлений R 1 и R 2 равными соответственно 10000 и 101,0101 Ом. Величина аргумента равна нулю, а величина логарифмического модуля рассчитывается по формуле

L = 20lg ( 1 + R1/ R 2 ) . (9)

Подставляя значения сопротивлений, получим теоретическое значение логарифмического модуля, равное 40 дБ . Рассмотрим результаты практического исследования технического объекта. Предположим, что ЦАП генерирует гармонический сигнал высокой точности единичной амплитуды без фазового смещения, блоки АЦП являются 16-разрядными устройствами, а в канале X включён усилитель с коэффициентом усиления 100.

Проведем исследование на генерируемой частоте 3 Гц в течение одной секунды . Графики входного и выходного сигналов представлены на рис . 2.

Для полученной выборки сигналов последовательно применяются формулы с (4) по (8). Получим результаты вычислений и рассчитаем погрешность результатов относительно их теоретических значений:

L_r1 = 36,852 дБ, ф _{R 1} = 0,809 ^O ,

5 R1 =

^LR1 ^l

L

• 100 % = 7,87%, Aф _R 1 = 0,809 O .

и

L = 10lg

(Re Y )2 +(Im Y )2 (Re X )2 +(Im X )2

ф = arctg

Im Y ^

Re Y J

( Im X - arctg

I Re X

Погрешности измерения обусловлены включением в измерительную цепь канала X усилителя, который не только усиливает полезный входной сигнал, в котором присутствуют помехи, но и вносит случайные составляющие. Кроме того, вычисление значений функций синуса и косинуса для каждого значения выборки приводит к накопле-

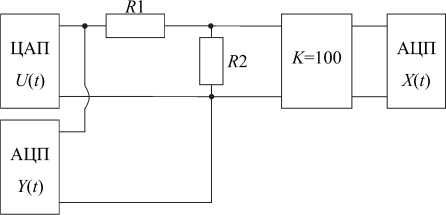
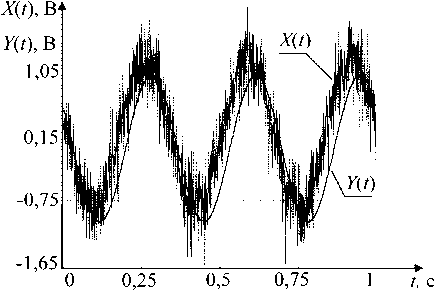
Рис. 2. Графики входного и выходного сигналов объекта

Рис. 1. Схема исследования технического объекта

Метод повышения точности определения частотных характеристик технических объектов нию дополнительной погрешности, связанной с неточностью представления значений функций в вычислительном устройстве.

Для снижения погрешностей возможно применение дополнительных расчётов, состоящих в накоплении фиксированного числа выборок и с последующим нахождением их среднего значения. Полученное от АЦП дискретное значение сигнала с учётом значения текущей фазы генератора добавляется к 32-разрядному значению в массиве (значение фазы генератора является номером элемента массива), который до начала измерения принимается нулевым. Кроме того, для каждого элемента массива ставится в соответствие 16-разрядная переменная, равная числу накопленных значений входных выборок в текущем элементе массива. Тогда на хранение каждого элемента требуется минимум 48 бит или, в случае хранения значений функции синус для четверти периода, 52 бит. По окончании измерения каждое накопленное значение необходимо разделить на их число для получения усредненного значения для текущей фазы.

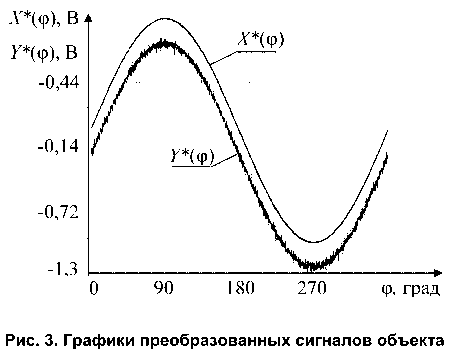
Так как в системе используются 16-разрядные устройства АЦП и ЦАП, то дискретное значение фазы генератора находится в диапазоне от 0 до 65535. В связи с необходимостью хранения информации объёмом более 384 кБ следует уменьшить данный диапазон до приемлемых величин. Уменьшение размера массива до 2048 элементов приведет к некоторому увеличению погрешности, но позволит значительно сократить требуемый объём памяти до 13 кБ и ускорить процесс вычислений в 32 раза. Полученные усреднённые значения элементов массива представляются в виде функциональной зависимости амплитуды от фазы (рис. 3).

Заключение

Сравнивая результаты двух экспериментов, следует, что применение дополнительных расчётов позволяет снизить относительную погрешность измерений логарифмического модуля до 0,21 %.

Получим результаты применения дополнительного расчёта:

L R 2 - 39,916 дБ, _ф R 2 - 0,0002 ° ,

5 R 2 -

R2

L

• 100% - 0,21%.

А_{ф R} 2 - 0,0002 ° .

Таким образом, предложенный метод позволяет значительно повысить точность определения частотных характеристик технических объектов.